漫谈什么是解题

王惠



漫谈什么是解题

王惠

简单地说，解题就是求出未知结论的过程。罗增儒先生说：“解题就是解决问题，即求出数学题的答案。这个答案在数学上也叫做解。所以，解题就是找出题的解的活动。小至一个学生算出作业的答案，一个教师讲完概念的构建与定理的证明，大至一个数学课题得出肯定或否定的结论，一个数学技术应用于实际、构建出适当的模型等，都叫做解题。”

波利亚发现，在日常解题和攻克难题而获得数学上的重大发现之间并没有不可逾越的鸿沟。他说：“一个重大的发现可以解决一些重大的问题，但在求解任何问题的过程中，都会有点滴的发现。”“一个有意义的题目的求解，为解此题所花的努力和由此得到的见解，可以打开通向一门新的科学的大门。”

大家非常熟悉的哥尼斯堡七桥问题，欧拉解决了，也就是说，欧拉解答了这个问题，由此创立了图论这个数学分支，即诞生了新的科学。像这样的例子，在数学上不胜枚举。这就验证了波利亚上面的论述。

波利亚主张把解题作为培养学生的数学才能和教会他们思考的一种手段与途径。这一主张得到了国际数学教育界的赞同。1976年，国际数学管理者委员会把解题能力列为十项基本技能的首位，美国数学教师联合会理事会把解题提到了“1980年代学校数学教学的核心”之高度。可见，解题对数学学习的重要。

例1“！”表示阶乘运算，如2！=2×1，3！=3×2× 1，求！的值。

分析：将各阶乘数转化为乘法运算，并找出消掉一些数的方法。不然的话，直接计算会相当繁杂，也不是此题的本意。这就联想到阶乘运算中的公式：n· n！=（n+1）！-n！。通过观察可知，公式左边有点像题目的左边，右边出现了减法，那就有可能消掉某些数。沿着这个思路试试，也许会有惊喜。

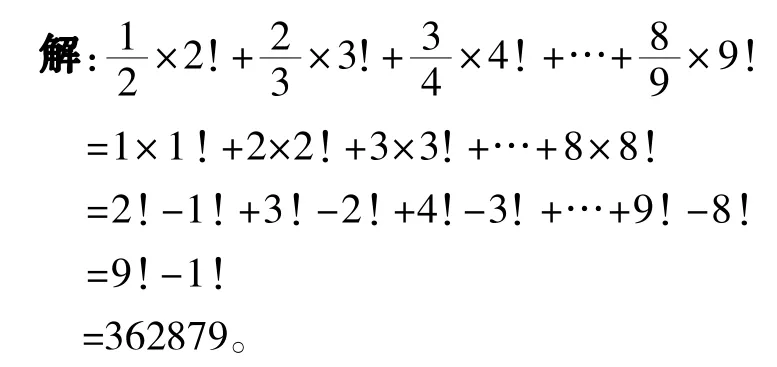
例2n是自然数，n2+n+11是素数吗？

分析：目前还没有表示所有素数的公式，那么，可以肯定所表示的数不可能全是素数。这就需要找出n2+n+11能表示哪些素数。解题方向明确了，我们就可以开始寻找解题方法。显然，n2+n+11在实数范围内不能分解因式，我们只能采取取值办法一一验证，找到结论。

解：记（fn）=n2+n+11，则分别令n=1，2，3，4，5，6，（fn）的值为13，17，23，31，41，53。显然这些数都是素数。是不是（fn）表示的所有的数都是素数？还需要继续验证。

令n=7，8，9，（fn）分别为67，83，101。还要验证吗？要！

令n=10，（fn）=121=112，不是素数！

因此，n2+n+11所表示的数不全是素数。

例350条直线最多能将平面分成多少部分？

分析：50条直线，多了点吧？画出50条直线来找答案，估计难以找到一个会这样解的人！怎么办？先画几条直线，从中找找分平面数的规律。

解：分别作出1条～5条直线分平面的情况，见下图。

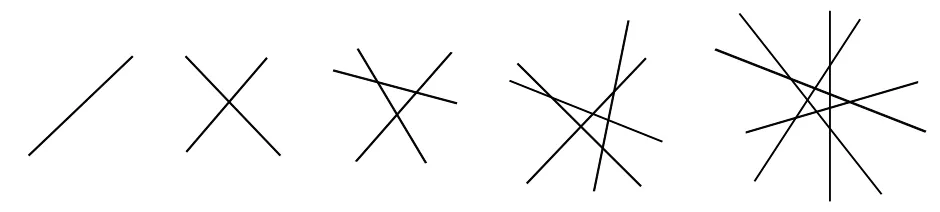
它们分平面的部分数分别为2，4，7，11，16。再将这5个数分解为2=1+1，4=1+1+2，7=1+1+2+3，11= 1+1+2+3+4，16=1+1+2+3+4+5。

这样，规律就凸显出来了。

我们从这3道题的解答过程中可以看到数学思维方法的运用。如灵活运用（n+1）！-n！=n·n！，将复杂的运算式子变得简便；要否定一个命题，只要举出一个反例即可；从最简单的情形出发，递推出结论。

解题过程中，很重要的一步就是要充分挖掘已知条件，显性的、隐性的都要充分利用。如例1中，等式（n+1）！-n！=n·n！是不可能告诉你的，必须根据阶乘的运算挖掘出来。如果没有这个等式的运用，计算量将会大大增加。事实上，由条件挖掘隐性的东西是成功解题的关键。

（作者单位：安乡县围庵小学）