催化剂颗粒形状对甲烷水蒸气重整反应的影响及工业反应器模拟

秦雯，周志明，程振民（华东理工大学化学工程联合国家重点实验室, 上海 200237）

催化剂颗粒形状对甲烷水蒸气重整反应的影响及工业反应器模拟

秦雯，周志明，程振民
（华东理工大学化学工程联合国家重点实验室, 上海 200237）

摘要：甲烷水蒸气重整工艺是现阶段最主要的工业制氢技术，催化剂颗粒形状和反应器操作条件是影响重整反应器性能和产物组成的重要因素。首先从颗粒尺度研究催化剂形状对甲烷水蒸气重整反应的影响，在不同的反应温度和压力下，计算并比较了球形、柱形和环形催化剂的效率因子，其大小顺序为：柱形 < 球形 < 环形。其次，将反应器床层的质量、热量和动量传递与环形催化剂颗粒的扩散-反应方程相结合，建立了用于描述甲烷水蒸气重整工业反应器的一维轴向数学模型。计算并分析了反应器进口温度和压力对反应器床层的温度和压力分布、催化剂效率因子以及甲烷转化率和各组分浓度分布的影响，确定了适宜的工业反应器进口温度和压力，分别为773 K 和3 MPa。

关键词：甲烷水蒸气重整反应；催化剂；反应器；扩散；效率因子；数学模拟

2015-08-03收到初稿，2015-11-06收到修改稿。

联系人：周志明。第一作者：秦雯（1993—），女，硕士研究生。

Received date: 2015-08-03.

引　言

甲烷水蒸气重整工艺是现阶段最简单、最经济同时也是最主要的工业制氢技术，它通常采用Ni基负载型催化剂，在固定床管式反应器内进行。鉴于该技术具有很大的实际应用价值，长期以来，相关催化剂的设计和反应器的模拟优化一直受到学术界和工业界的关注[1-4]。

在催化剂设计方面，研究者更多的关注于活性组分[5-6]、载体[7-8]、制备方法[9-10]等，目的是抑制催化剂积炭和活性组分烧结[4,11]，提高催化剂的使用寿命。上述研究大多在实验室规模的反应器内进行，催化剂装填量少，而且为了尽可能减小催化剂内扩散的影响，研究者通常使用粉末状催化剂。然而，粉末状催化剂的床层压降大，并不适用于工业固定床反应器，必须对催化剂粉末进行成型处理。成型催化剂的颗粒形状（球形、柱形、环形等）是影响反应过程和反应器操作的重要因素，除了颗粒自身的机械强度和流体力学方面（如流体流动、压力降等）的考虑外，由于颗粒形状的不同所引起的催化剂内扩散影响的差异，也不容忽视[12]。针对甲烷水蒸气重整制氢反应体系，现有的大多数研究都是基于单一形状的催化剂颗粒[13-16]，只有少数研究者[17-18]比较了不同形状的催化剂颗粒对甲烷重整反应的影响。

最近，本课题组[19]采用共沉淀法制备了Ni/MgAl(O)催化剂粉末，与传统的Ni/Al2O3相比，它在甲烷水蒸气重整反应中表现出更高的活性和稳定性，尤其是当Ni:Mg:Al（原子比）为0.5:2.5:1时，其活性达到最高，为了进一步拓展该催化剂的工业应用前景，本文将研究催化剂颗粒形状对甲烷水蒸气重整反应的影响，为工业重整反应器的设计和优化操作提供理论支持。

1　数学模型的建立

本文针对球形、柱形和环形3种典型的催化剂颗粒开展研究，基于文献[13,20]关于工业用甲烷水蒸气重整催化剂的报道，确定了3种催化剂颗粒的几何尺寸（图1），它们具有相同的体积。为了简便起见，假设活性组分在催化剂颗粒内部均匀分布。事实上，如果对采用共沉淀法制得的Ni/MgAl(O)催化剂粉末直接进行成型处理，所得到的催化剂便是活性组分均匀分布的颗粒。

图1　球形、柱形和环形Ni/MgAl(O)催化剂颗粒Fig. 1　Spherical-, cylindrical- and ring-shaped Ni/MgAl(O) catalyst pellets

1.1反应动力学模型

针对Ni/MgAl(O)催化剂，本课题组已经建立了甲烷水蒸气重整反应动力学模型[19]，该模型具有热力学一致性且能较好地描述实验数据。下面简要给出该动力学模型及相关参数，具体的公式推导和参数估值方法见文献[19]。对于甲烷水蒸气重整反应体系，主要考虑以下3个反应

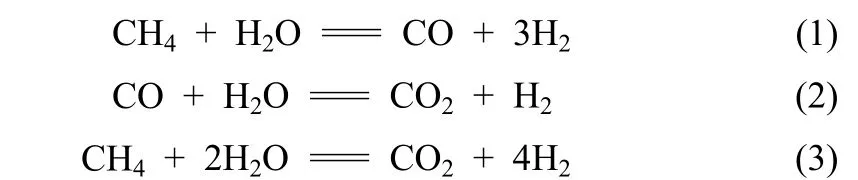
上述反应分别是蒸气重整反应[式（1）和式（3）]和水气变换反应[式（2）]，其对应的反应速率表达式分别为

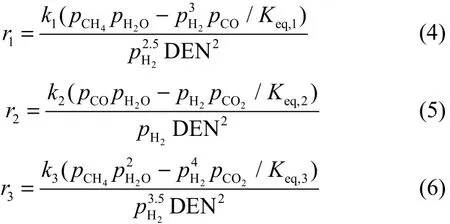
其中

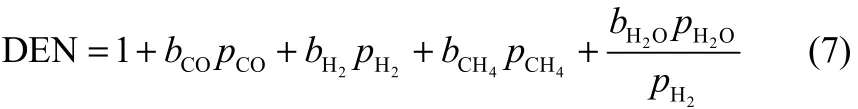
式中，Keq,i表示第i个反应的平衡常数，可分别由式（8）～式（10）计算得到[21]

上述反应速率方程式所含的ki和bj分别表示第i个反应的速率常数和第j个组分的吸附平衡常数。根据Arrhenius方程，ki和bj可分别表示为

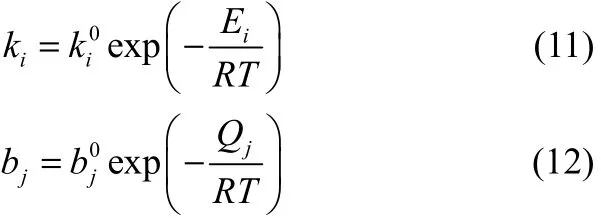
通过实验数据并采用非线性最小二乘拟合，可以获得相应的动力学常数（表1）和吸附常数（表2）。

表1　动力学常数的估计值Table 1　Estimated kinetic constants

表2　吸附常数的估计值Table 2　Estimated adsorption constants

1.2催化剂颗粒内部的扩散-反应模型

对于工业用甲烷水蒸气重整催化剂，由于颗粒尺寸较大，催化剂内扩散的影响不可忽略[13-14]。当反应过程处于稳态时，对催化剂颗粒内部的微元段进行质量衡算，便可得到气相组分j的扩散-反应方程

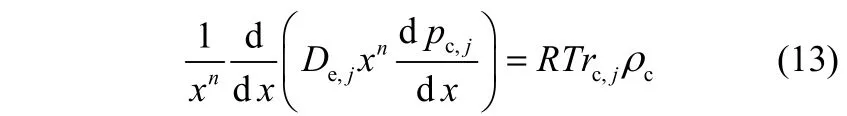
式中，pc,j和rc,j分别表示组分j在催化剂内部的分压和反应速率；ρc为催化剂颗粒密度，其值设为2350 kg·m−3[13]；n的取值与催化剂的形状有关。对于片形、柱形以及球形催化剂，n的取值分别为0、1和2[12,22]。需要说明的是，对于环形催化剂颗粒，可以将其视为片形（将其沿轴向剪切并展开），故环形催化剂所对应n值为0。此外，对于柱形和环形催化剂，为简化起见，假设催化剂颗粒为无限长，只考虑反应物和产物沿催化剂侧面进行扩散，因此式（13）为近似的扩散-反应模型。催化剂颗粒内部组分j的有效扩散系数De,j可由式（14）计算

式中，εc和τc分别表示催化剂颗粒的孔隙率和曲折因子，参照文献[23]，εc和τc分别取值为0.5和4；Djm为混合物中组分j的综合扩散系数，对于大多数工业催化剂，通常只需考虑分子扩散和Knudsen扩散的贡献，其计算公式如下[12]

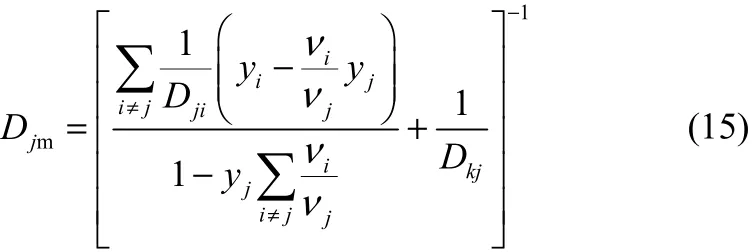
式中，yj表示组分j的摩尔分数，。在甲烷水蒸气重整制氢反应体系所涉及的3个反应中，独立反应数为2，因此，只需知道两个关键组分的分压，便可计算出其他组分。本文选取CH4和CO2为关键组分，其对应的扩散-反应方程分别为

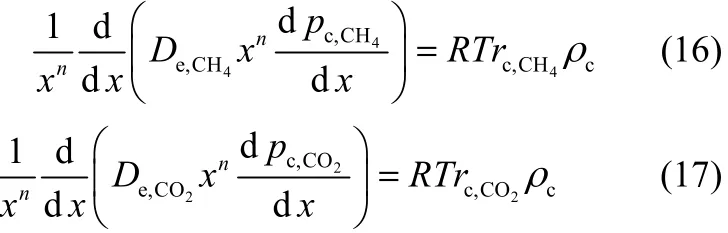
式中，rc,CH4=rc,1+rc,3，rc,CO2=−rc,2−rc,3。上述方程的边界条件为：

x=0时

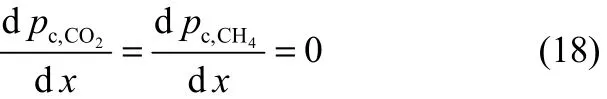
x=dc/2 (球形，柱形)或x=(dc,out−dc,in)/4 (环形)时

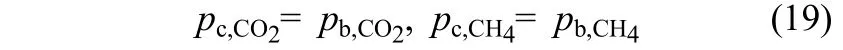
式中，pb,CO2和pb,CH4分别表示气相主体中的CO2和CH4分压。此处，催化剂外扩散的影响并未计入，这是因为在工业重整反应器中，气体线速度较大，Reynolds数通常大于5000[24]，因此可忽略外扩散影响[13,15,25]。

在此基础上，可计算得到各个反应所对应的效率因子

式中，rb,i为按气相主体组分浓度计算的反应速率。

1.3工业反应器模型

甲烷水蒸气重整工业反应器的长度通常为10～13 m，外直径为10～20 cm，对于这类反应器，Rostrup-Nielsen等[24]指出：采用一维轴向模型和二维轴径向模型所得到的模拟计算结果相差无几；与反应器壁的温度梯度相比，反应器内部的径向温度梯度相对较小，只有在进行积炭研究时，才有必要采用二维模型。因此，本文采用相对简单的一维反应器模型。此外，对于工业重整反应器，由于气速大，轴向扩散的影响可忽略不计[24]。下面分别给出关键组分的连续性方程、能量衡算方程以及动量衡量方程

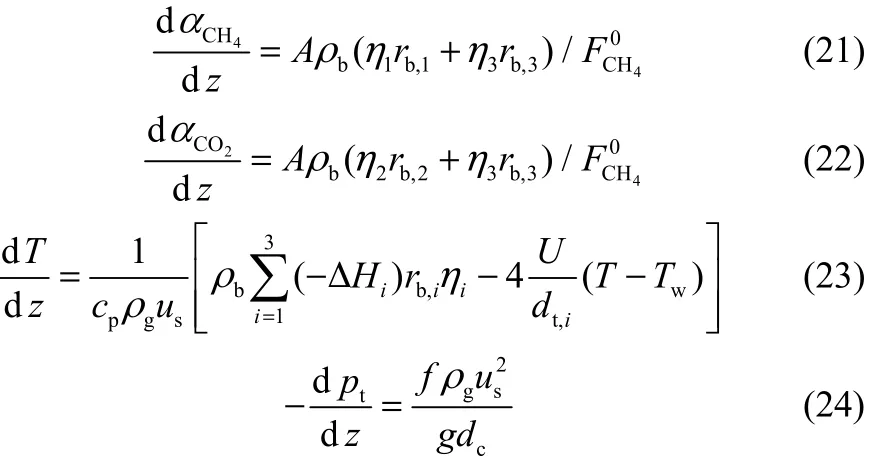
式中，αCH4和αCO2分别表示CH4和CO2的转化率；rb,i表示气相主体中第i个反应的速率；ρb为反应器床层密度，ρb=(1−εb)ρc。εb为床层空隙率，不同形状的催化剂颗粒所对应的床层空隙率不尽相同[12,26]，可由式（25）计算[26]

式（21）～式（24）的边界条件为

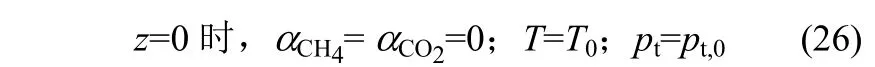
关键组分转化率、各组分分压和摩尔流量之间存在以下关系

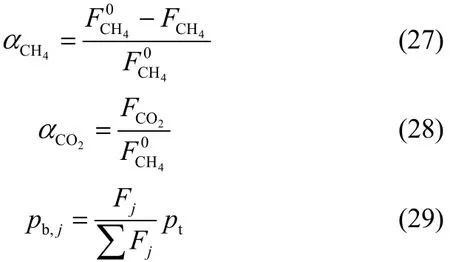
式（23）中的U表示传热系数，其计算公式如下

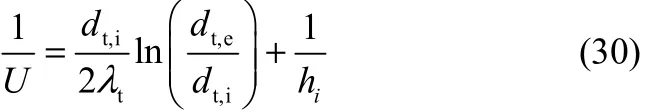
式中各参数的计算方法见文献[13]。式（24）中的f为摩擦系数，可由经典的Ergun方程计算得到

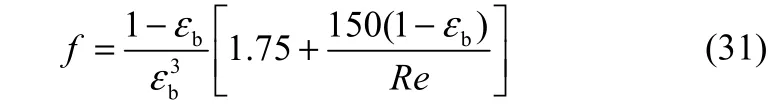
1.4数学模型的求解

对于催化剂颗粒内部的扩散-反应模型，采用正交样条配置法[22]计算颗粒内部的各组分压力分布和内扩散效率因子。样条点个数设为3，对于球形和柱形催化剂，其位置依次为x = 0, 0.7×dc/2, dc/2；对于环形催化剂，其位置分别为0, 0.7(dc,out−dc,in)/4, (dc,out−dc,in)/4。如此，中间样条点将整个求解区域划分成内、外两个子区域，每个子区域均采用Jacobi正交多项式来进行插值，其中内部区域的插值点（配置点）个数取为10，外部区域的配置点个数为12。

对于反应器模型，按照每段1 cm的长度将整个反应器沿轴向进行等距划分，对于每一小段，采用四阶Runge-Kutta法计算气相主体的组分浓度、温度和压力。需要说明的是，由于每段反应器的长度很短，因此，每段床层内的催化剂效率因子可视为不变，等于该段进口端所对应的效率因子。数学模型求解过程中使用到的物性数据见文献[21]。

2　结果与讨论

2.1催化剂颗粒形状的影响

在气相组成一定的情况下，针对3种不同形状的催化剂颗粒，分别考察反应温度和压力对催化剂效率因子的影响，气相中CH4:H2O:H2:CO2:CO的摩尔比设为16:60:18.5:5:0.5。图2给出了气相压力为2 MPa时，不同形状的催化剂颗粒在不同温度下的效率因子。由图可见，随着反应温度的升高，3种催化剂的效率因子均减小，这是因为温度对反应速率的影响大于其对扩散速率影响的缘故，这与Baek 等[27]的报道相符。此外，在相同操作条件下环形催化剂的效率因子总是优于球形或柱形催化剂。在上述假设的反应条件下，反应式（1）和反应式（3）的效率因子为正，而反应式（2）的为负，说明水气变换反应的方向发生了改变，2.2节将对此进行讨论。

图2　不同形状催化剂颗粒的效率因子随反应温度的变化Fig. 2　Variation of shape-dependent effectiveness factors of various catalysts with temperature

图3给出了反应温度为973 K时，不同形状的催化剂颗粒在2、2.5和3 MPa下的效率因子。由图可见，随着气相压力的增大，球形、柱形和环形催化剂的效率因子均增大，这与Hallajbashi等[28]的报道相一致。同样地，反应式（2）的效率因子为负。在上述3种催化剂中，环形颗粒的效率因子依旧最高。因此，在后续的工业反应器模拟中，将采用环形催化剂颗粒来考察主要操作变量对甲烷水蒸气重整制氢的影响。

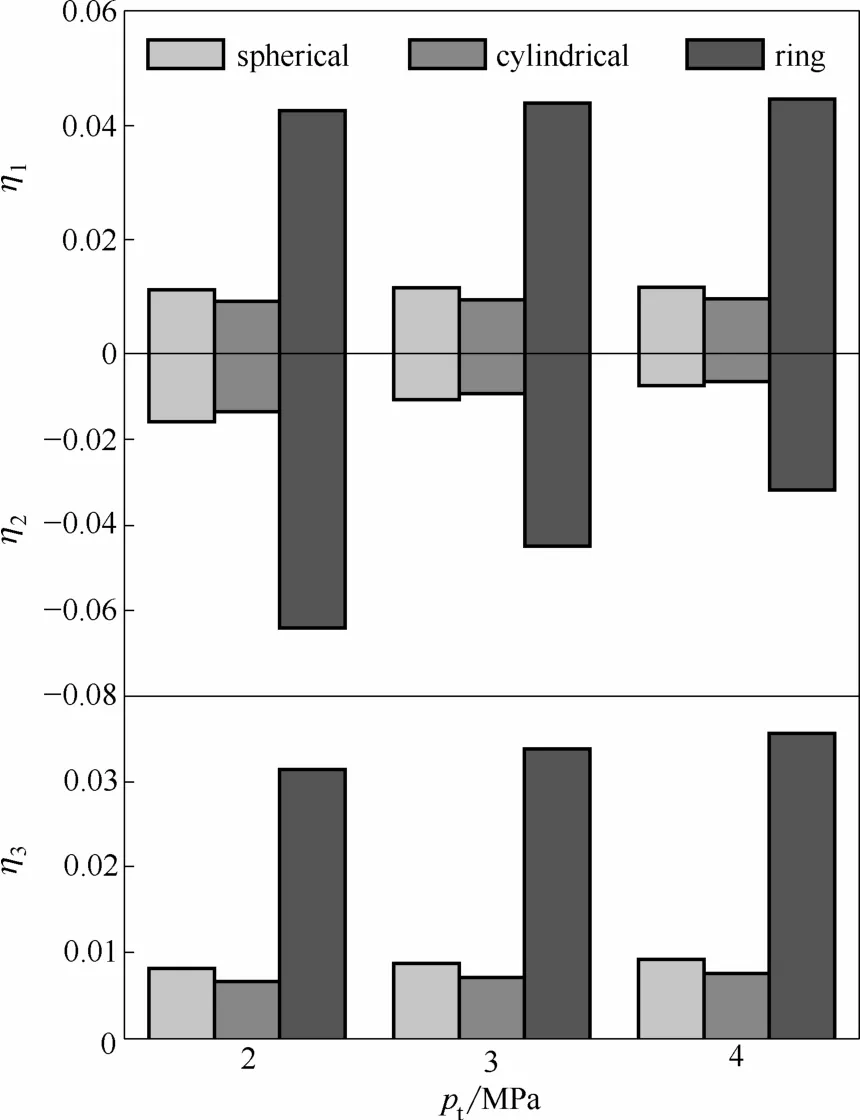
图3　不同形状催化剂颗粒的效率因子随反应压力的变化Fig. 3　Variation of shape-dependent effectiveness factors of various catalysts with pressure

结合图2和图3可知，不同形状催化剂效率因子的大小顺序为：环形 > 球形 > 柱形，这与它们的比表面积大小顺序一致（环形、球形和柱形催化剂的比表面积分别为769、397和325 m−1，此处只计入环形和柱形催化剂的侧面积），表明催化剂比表面积的差异导致了催化剂效率因子的差别。这是因为催化剂的比表面积对传质的影响较大，而效率因子即是反映传质对反应速率的影响。由图2和图3进一步可见，工业催化剂颗粒的效率因子普遍很低，即便是环形催化剂也不例外。图4显示了环形催化剂颗粒内部各组分的摩尔分数变化，在催化剂外表面附近各组分的浓度梯度变化剧烈，这充分说明催化剂的内扩散影响较为严重。

图4　环形催化剂颗粒内部各组分摩尔分数的变化Fig. 4　Variation of molar fraction of various species inside ring-shaped catalyst pellet

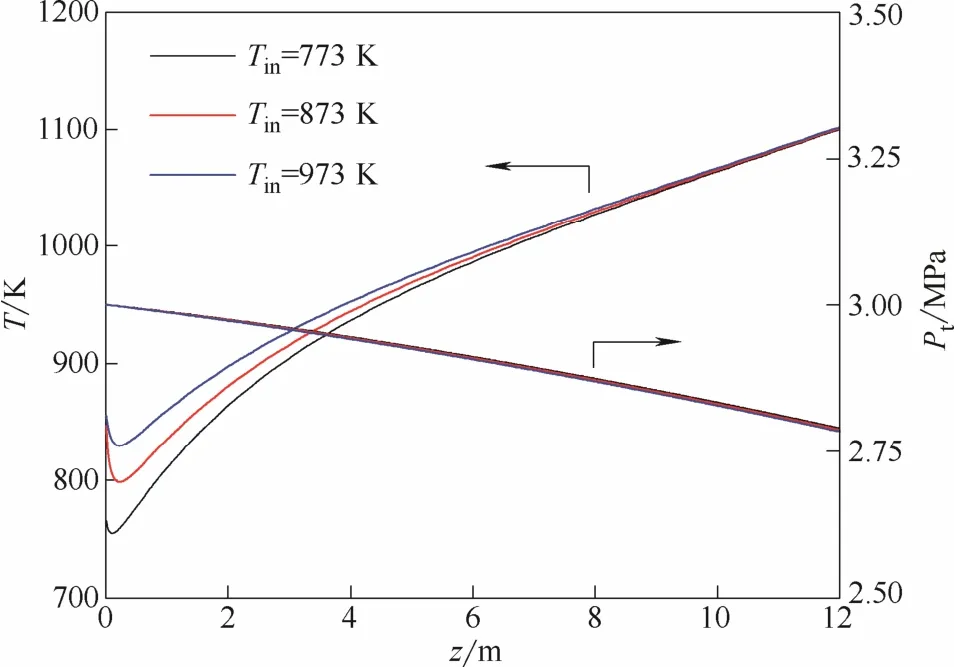
图5　反应器内的气相温度和压力分布（进口压力3 MPa）Fig. 5　Profiles of gas temperature and pressure in reactor (inlet pressure 3 MPa)

图6　环形催化剂效率因子沿反应器轴向的变化（进口压力3 MPa）Fig. 6　Variation of effectiveness factors of ring-shaped catalyst along reactor (inlet pressure 3 MPa)

2.2工业反应器的模拟

本文对甲烷水蒸气重整制氢工业反应器的结构尺寸和进料组成做以下规定：①工业反应器的长度、内径和壁厚分别为12、0.1和0.015 m，这与Xu等[13]以及Pantoleontos等[15]采用的重整反应器相似；②参照Alberton等[29]使用的原料气组成，假设反应器进口物料中的CH4、H2O和H2的摩尔分数分别为0.24、0.75和0.01，进口总流量为25 kmol·h−1；③参考Xu等[13]的报道，假设反应器外壁温度沿轴向呈线性增加的规律，且在反应器进、出口处分别为973和1173 K。

2.2.1进口温度的影响图5给出了当反应器进口压力恒定为3 MPa而进口温度分别为773、873和973 K时，反应器内的温度和压力分布。由图可见，气体温度呈先降低（0 ≤ z < a）后升高（z ≥ a）的趋势（进口温度773、873和973 K所对应a的值分别为0.11、0.22和0.23 m），这主要是因为甲烷水蒸气重整反应是强吸热反应，在反应初期，由炉膛经反应器壁提供的热量并不足以维持重整反应所需的热量，因此气相温度有所降低；但是随着反应进行，水气变换这一放热反应慢慢突显，同时反应器外壁温度也逐渐升高，故气相温度转而上升。反应器内的压力变化与进口温度的大小关系不大，不同温度下的压力分布曲线几乎重合。此外，整个反应器的床层压降约为0.21 MPa，占反应器进口压力的7.0%。

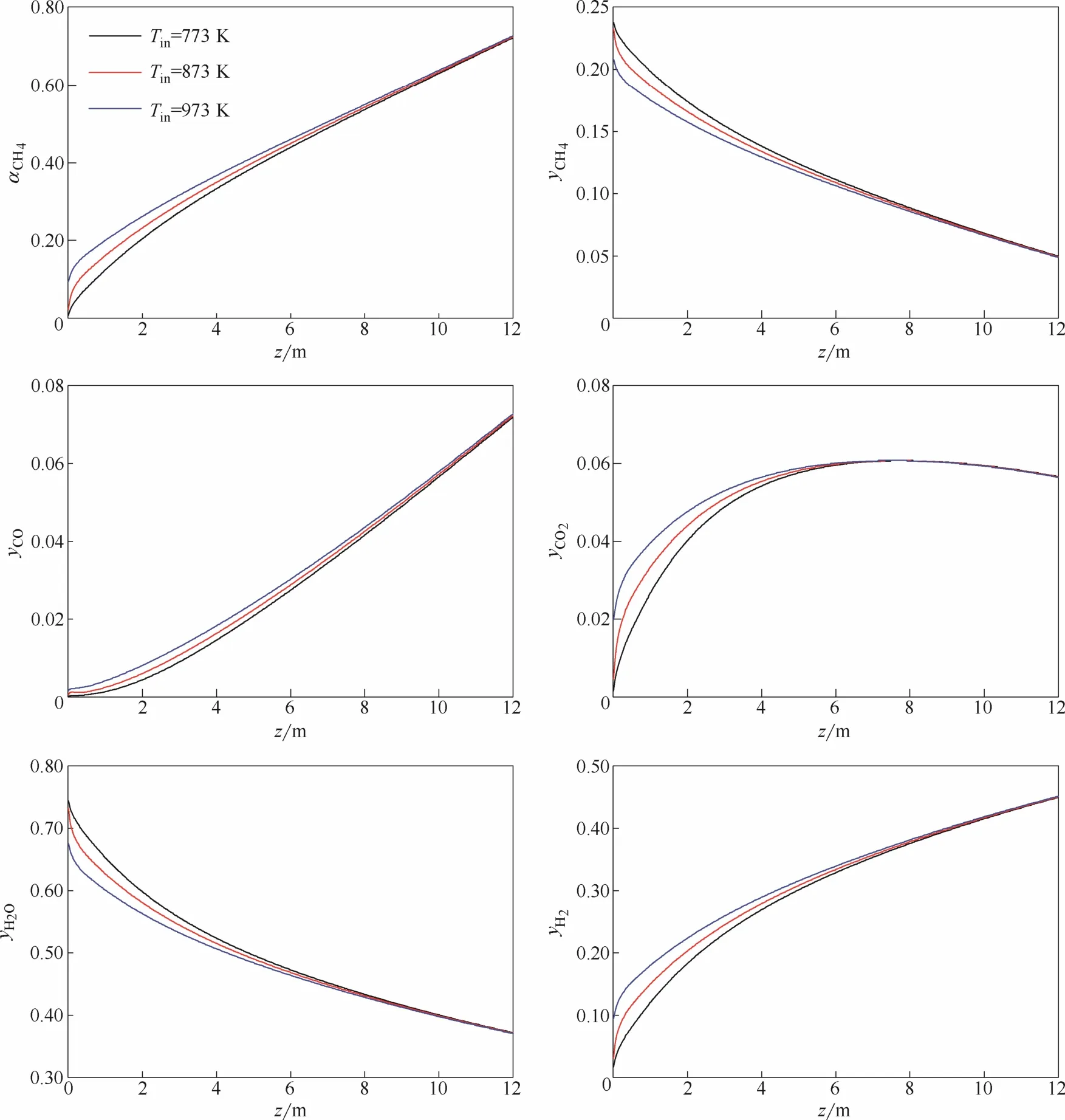
图7　甲烷转化率和各组分摩尔分数沿反应器轴向的变化（进口压力3 MPa）Fig. 7　Variation of conversion of CH4and molar fraction of various species along reactor (inlet pressure 3 MPa)

图6为不同进口温度下的催化剂效率因子沿反应器轴向的变化情况。对于蒸气重整反应[式（1）和式（3）]，其效率因子（η1和η3）的变化规律与图5所示的温度变化相互呼应，即η1和η3先迅速增大后逐渐减小。此外，随着进口温度的升高，η1和η3均呈现减小的趋势，尤其是在反应器的前半段。对于水气变换反应[式（2）]，其效率因子（η2）在距离反应器进口约2.3 m（773 K）、1.8 m（873 K）和1.2 m（973 K）处出现了由正值向负值的突变，随后又分别在7.5、7.1和6.9 m处由负变正，这主要是因为催化剂颗粒表面和内部的水气变换反应方向发生改变所致。前一个突变对应于催化剂表面的水气变换由正反应向逆反应方向转变，此时颗粒内部的水气变换反应方向不变；而后一个变化则对应于催化剂内部的水气变换反应方向由正向逆转变，此时催化剂表面仍进行逆水气变换反应。这一现象与Xu等[13]、Pantoleontos等[15]的报道相符。

图7进一步给出了不同进口温度下的甲烷转化率和各组分摩尔分数沿反应器轴向的变化。由于甲烷水蒸气重整反应是吸热反应，较高的进口温度对提高甲烷转化率显然有利，但是随着反应的推移，在反应器的后段床层，不同进口温度下的甲烷转化率渐趋一致。上述变化趋势也可以从反应器内各组分的浓度分布曲线得以体现。尽管在反应器前段不同进口温度所对应的组分浓度差异较大，但是随着催化剂床层长度的增加，不同进口温度下的气相温度趋于一致（图5），从而使得反应器后段的各组分浓度曲线重合。

综上所述，一方面升高反应器进口温度可以在一定区域内提高甲烷转化率，但是同时也会降低催化剂的效率因子；另一方面，由于工业重整反应器的床层足够长，不同进口温度所对应的出口甲烷转化率和各组分浓度差异很小。因此，宜选择相对较低的进口温度（773 K）来进行工业化生产，这也有利于降低能耗和对设备材料的要求。

2.2.2进口压力的影响图8给出了当反应器进口温度恒定为773 K而进口压力分别为2、3和4 MPa时，反应器内的温度和压力分布。由图可见，床层温度随进口压力的增大而升高，这是因为：一方面，甲烷水蒸气重整制氢是分子数增加的反应，提高进口压力对正反应不利，因此反应所需的热量减少，而用于加热气体的热量相应地增加；另一方面，加压可以增加气相介质密度，使Reynolds数增大，进而提高床层给热系数，对传热有利[30]。进一步比较各温度分布曲线可以发现，进口压力3 MPa和4 MPa所对应的温度分布较为接近。此外，在进口压力2～4 MPa范围内，反应器的床层压降均不高。

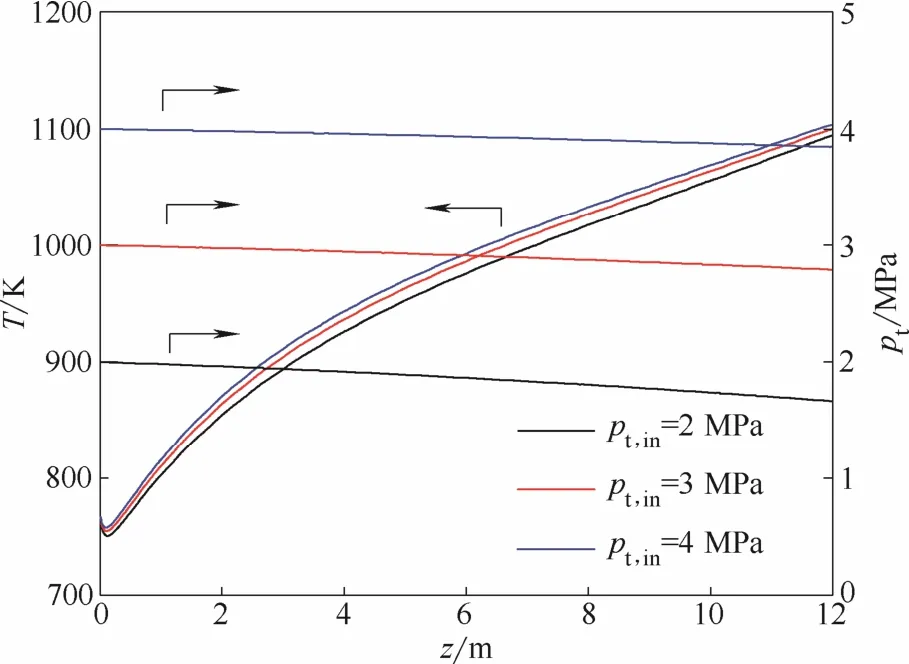
图8　反应器内的气相温度和压力分布（进口温度773 K）Fig. 8　Profiles of gas temperature and pressure in reactor (inlet temperature 773 K)

图9　环形催化剂效率因子沿反应器轴向的变化（进口温度773 K）Fig. 9　Variation of effectiveness factors of ring-shaped catalyst along reactor (inlet temperature 773 K)

图9显示了不同进口压力下的催化剂效率因子沿反应器轴向的变化。总体而言，增大进口压力有助于提高重整反应的效率因子，但是3 MPa和4 MPa对应的效率因子曲线相差不大。至于水气变换反应，其效率因子的变化规律与图6相似，此处不再赘述。需要指出的是，与进口温度的影响相比，进口压力对催化剂效率因子的影响并不显著。

图10给出了不同进口压力下的甲烷转化率和各组分摩尔分数沿反应器轴向的变化。显而易见，对于分子数增大的甲烷水蒸气重整反应，提高反应压力将导致甲烷转化率降低。此外，与进口压力由2 MPa增加至3 MPa时各组分的摩尔分数变化相比，当压力由3 MPa进一步升高至4 MPa时，各组分的摩尔分数变化幅度有所减小。对应于2、3和4 MPa，反应器出口的氢气流量分别为16.8、15.1和14.0 kmol·h−1，显然，增加压力对于提高氢气产量不利。

图10　甲烷转化率和各组分摩尔分数沿反应器轴向的变化（进口温度773 K）Fig. 10　Variation of conversion of CH4and molar fraction of various species along reactor (inlet temperature 773 K)

综上，从热力学特征看，低压有利于提高甲烷转化率和氢气产量，但是从动力学角度看，高压对增大催化剂效率因子有利。此外，从工程角度考虑，由于甲烷水蒸气重整反应过程需要外部供热，大的给热系数是强化传热的前提，而适当增加压力对传热有利。鉴于3 MPa和4 MPa对应的催化剂效率因子接近，而前者的甲烷转化率更高且对设备材料的要求相对较低，所以宜选择3 MPa的进口压力来操作工业反应器。

3　结　论

（1）在甲烷水蒸气重整制氢反应中，球形、柱形和环形Ni/MgAl(O)催化剂颗粒的效率因子均与反应温度呈负相关，与反应压力呈正相关；3种形状催化剂效率因子的大小顺序为：环形 > 球形 >柱形。

（2）甲烷水蒸气重整过程中的3个主要反应的吸放热情况不尽相同，其效率因子也存在差异。其中，蒸气重整反应[式（1）和式（3）]的效率因子均为正值且相差不大，而水气变换反应[式（2）]的效率因子时正时负，取决于具体的反应条件。

（3）操作条件的确定是工业生产中一项重要内容。对于本文重点研究的环形催化剂，将其装填入反应器进行生产时，优选的工业重整反应器进口温度和压力分别为773 K和3 MPa。

符号说明

A ——反应器横截面积，m2

bj——组分j的吸附常数，bCH4、bCO和bH2的单位

为kPa−1，bH2O为量纲1

cp——工艺气体的比热容，J·g−1·K−1

dc——催化剂颗粒直径（球形和柱形），m

dc,in, dc,out——分别为环形催化剂内径、外径，m

dce——颗粒当量直径，m

dt,i, dt,e——分别为反应器内径、外径，m

De,j——组分j的有效扩散系数，m2·s−1

E ——活化能，kJ·mol−1

Fj,F0

j——分别为组分j的瞬时流量和初始流量，kmol·h−1

f ——动量方程中的摩擦系数

ΔHi——第i个反应的焓变，kJ·mol−1

hi——给热系数，J·m−2·h−1·K−1

Keq,i——第i个反应的平衡常数，bar2[式（1）和式

（3）]、量纲1[式（2）]

ki——第i个反应的速率常数，k1、k2和k3的单位分别为mol·kPa0.5·kg−1·s−1、mol·kg−1·s−1·kPa−1以及mol·kPa0.5·kg−1·s−1

pb,j——气体主体中组分j的分压，MPa

pc,j——催化剂颗粒内部组分j的分压，MPa

pt——总压，MPa

Qj——组分j的吸附热，kJ·mol−1

Re ——Reynolds数

r, rc, rb——分别为反应速率、催化剂内部的反应速率和

气相主体的反应速率；mol·kg−1·s−1

T ——气相主体温度，K

Tw——反应器外壁温度，K

U——传热系数，J·m−2·h−1·K−1

us——表观速率，m·s−1

V——催化剂体积，m3

x——催化剂颗粒径向位置坐标，m

z——反应器轴向位置坐标，m

αCH4, αCO2——分别为CH4和CO2的转化率

εb——床层空隙率

εc——催化剂颗粒孔隙率

ηi——第i个反应的效率因子

λt——热导率，J·m−1·h−1·K−1

ρb——反应器床层密度，kg·m−3

ρg——气相密度，kg·m−3

ρs——催化剂颗粒密度，kg·m−3

τc——催化剂曲折因子

References

[1] 阳宜洋, 丁石, 金涌, 等. Rh/MgO/γ-Al2O3上的毫秒级甲烷蒸汽重整过程 [J]. 化工学报, 2009, 60(8): 1981-1987. YANG Y Y, DING S, JIN Y, et al. Milliseconds steam reforming of methane using Rh/Mgo/γ-Al2O3catalyst [J]. CIESC Journal, 2009, 60(8): 1981-1987.

[2] ANGELI S D, MONTELEONE G, GIACONIA A, et al. State-of-the-art catalysts for CH4steam reforming at low temperature [J]. Int. J. Hydrogen Energy, 2014, 39(5): 1979-1997.

[3] ARCOTUMAPATHY V, SIAHVASHI A, ADESINA A A. A new weighted optimal combination of ANNs for catalyst design and reactor operation: methane steam reforming studies [J]. AIChE J., 2012, 58(8): 2412-2427.

[4] LI S R, GONG J L. Strategies for improving the performance and stability of Ni-based catalysts for reforming reactions [J]. Chem. Soc. Rev., 2014, 43(21): 7245-7256.

[5] MALUF S S, ASSAF E M. Ni catalysts with Mo promoters for methane steam reforming [J]. Fuel, 2009, 88(9): 1547-1553.

[6] DUARTE R B, KRUMEICH F, VAN Bokhoven J A. Structure, activity, and stability of atomically dispersed Rh in methane steam reforming [J]. ACS Catal., 2014, 4(5): 1279-1286.

[7] KIM H W, KANG K M, KWAK H Y, et al. Preparation of supported Ni catalysts on various metal oxides with core/shell structures and their tests for the steam reforming of methane [J]. Chem. Eng. J., 2011, 168(2): 775-783.

[8] FAURE R, ROSSIGNOL F, CHARTIER T, et al. Alumina foam catalyst supports for industrial steam reforming processes [J]. J. Europ. Ceram. Soc., 2011, 31(3): 303-312.

[9] TAKEHIRA K. “Intelligent” reforming catalysts: trace noble metal-doped Ni/Mg(Al)O derived from hydrotalcites [J]. J. Nat. Gas Chem., 2009, 18(3): 237-259.

[10] JIMENEZ-GONZALEZ C, BOUKHA Z, DE RIVAS B, et al. Behaviour of coprecipitated NiAl2O4/Al2O3catalysts for low-temperature methane steam reforming [J]. Energy & Fuels, 2014, 28(11): 7109-7121.

[11] TRIMM D L. Catalysts for the control of coking during steam reforming [J]. Catal. Today, 1999, 49(1/2/3): 3-10.

[12] FROMENT G F, BISCHOFF K B, WILDE J D. Chemical Reactor Analysis and Design[M]. 3rd ed. New Jersey: John Wiley & Sons,2011: 505-509.

[13] XU J G, FROMENT G F. Methane steam reforming(Ⅱ): Diffusional limitations and reactor simulation [J]. AIChE Journal, 1989, 35(1): 97-103.

[14] OLIVEIRA E L G, GRANDE C A, RODRIGUES A E. Methane steam reforming in large pore catalyst [J]. Chem. Eng. Sci., 2010, 65(5): 1539-1550.

[15] PANTOLEONTOS G, KIKKINIDES E S, GEORGIADIS M C. A heterogeneous dynamic model for the simulation and optimisation of the steam methane reforming reactor [J]. Int. J. Hydrogen Energy, 2012, 37(21): 16346-16358.

[16] ROUT K R, JAKOBSEN H A. Simulation of pellet model with multicomponent mass diffusion closure using least squares spectral element solution method [J]. Can. J. Chem. Eng., 2013, 91(9): 1547-1567.

[17] HARTMANN V L, OBYSOV A V, DULNEV A V, et al. New basic shape of catalysts for natural gas reforming reactors [J]. Chem. Eng. J., 2011, 176/177: 102-105.

[18] DIXON A G, BOUDREAU J, ROCHELEAU A, et al. Flow, transport, and reaction interactions in shaped cylindrical particles for steam methane reforming [J]. Ind. Eng. Chem. Res., 2012, 51(49): 15839-15854.

[19] QI Y, CHENG Z M, ZHOU Z M. Steam reforming of methane over Ni catalysts from hydrotalcite-type precursors: catalytic activity and reaction kinetics [J]. Chin. J. Chem. Eng., 2015, 23(1): 76-85.

[20] GHOUSE J, ADAMS T A. A multi-scale dynamic two-dimensional heterogeneous model for catalytic steam methane reforming reactors [J]. Int. J. Hydrogen Energy, 2013, 38(24): 9984-9999.

[21] YAWS C L. Chemical Properties Handbook[M]. New York: McGraw-Hill, 1999: 314-339.

[22] VILLADSEN J, MICHELSEN M L. Solution of Differential Equation Models by Polynomial Approximation[M]. New Jersey: Prentice-Hall, 1978: 273-294,417-440.

[23] SATTERFIELD C N. Heterogeneous Catalysis in Industrial Practice[M]. 2nd ed. New York: McGraw-Hill, 1991.

[24] ROSTRUP-NIELSEN J, CHRISTIANSEN L J. Concepts in Syngas Manufacture[M]. London: Imperial College Press, 2011: 149,162.

[25] SADOOGHI P, RAUCH R. Pseudo heterogeneous modeling of catalytic methane steam reforming process in a fixed bed reactor [J]. J. Nat. Gas Sci. Eng., 2013, 11: 46-51.

[26] BENYAHIA F, O’NEILL K E. Enhanced voidage correlations for packed beds of various particle shapes and sizes [J]. Particul. Sci. Technol., 2005, 23(2): 169-177.

[27] BAEK S M, KANG J H, LEE K J, et al. A numerical study of the effectiveness factors of nickel catalyst pellets used in steam methane reforming for residential fuel cell applications [J]. Int. J. Hydrogen Energy, 2014, 39(17): 9180-9192.

[28] HALLAJBASHI N, BAGHAEE M R. The effectiveness factor determination for a three hole cylindrical catalyst pellet in a steam methane reforming reaction [J]. Energ. Source Part A, 2014, 36(4): 366-373.

[29] ALBERTON A L, SCHWAAB M, FONTES C E, et al. Hybrid modeling of methane reformers(I): A metamodel for the effectiveness factor of a catalyst pellet with complex geometry [J]. Ind. Eng. Chem. Res., 2009, 48(21): 9369-9375.

[30] 朱志庆. 化工工艺学[M]. 北京: 化学工业出版社, 2007: 40-41. ZHU Z Q. Chemical Engineering Process[M]. Beijing: Chemical Industry Press, 2007: 40-41.

DOI：10.11949/j.issn.0438-1157.20151252

中图分类号：TQ 032; TQ 116.2+5

文献标志码：A

文章编号：0438—1157（2016）02—0563—10

基金项目：国家自然科学基金项目（21276076）；教育部新世纪优秀人才支持计划项目(NCET-13-0801)；中央高校基本科研业务费（222201313011）。

Corresponding author:Prof. ZHOU Zhiming, zmzhou@ecust.edu.cn supported by the National Natural Science Foundation of China (21276076), the Program for New Century Excellent Talents in University (NCET-13-0801) and the Fundamental Research Funds for the Central Universities (222201313011).

Influence of catalyst shape on methane steam reforming and simulation of industrial reactor

QIN Wen, ZHOU Zhiming, CHENG Zhenmin
(State Key Laboratory of Chemical Engineering, East China University of Science and Technology, Shanghai 200237, China)

Abstract:Methane steam reforming (MSR) is the most widely used technology for hydrogen production in industry now, where the shape of catalyst particles and the reactor operating conditions greatly influence the reactor performance and the product composition. Firstly, the present study investigated the effect of catalyst shape (sphere, cylinder and ring) on the MSR using a diffusion-reaction model on the particle scale. The effectiveness factors of shaped catalysts followed the sequence: cylinder < sphere < ring. Next, a one-dimensional mathematical model was developed by taking into account the mass, heat and momentum transfer on the reactor scale together with the diffusion-reaction equations on the catalyst scale, and used to describe an industrial MSR reactor. The effects of inlet temperature and pressure on the profiles of temperature and pressure inside the reactor, effectiveness factor, conversion of methane as well as concentration of various species were studied. Finally, the optimal inlet temperature and pressure for the industrial reactor were determined, being 773 K and 3 MPa, respectively.

Key words:methane steam reforming; catalyst; reactor; diffusion; effectiveness factor; mathematical modeling