门座式起重机臂架及自重平衡系统的优化设计研究

曹 娜

(天津港第五港埠有限公司 天津300456)

门座式起重机臂架及自重平衡系统的优化设计研究

曹 娜

(天津港第五港埠有限公司 天津300456)

随着经济的发展和国际物流业的繁荣，港口物流对门座式起重机装卸货物的效率、使用的安全可靠性等工作性能提出了更高的要求。因此，对门座式起重机各方面的研究一直是国内外的热点。四连杆铰接组合臂架变幅系统是目前应用较广泛的门座式起重机臂架形式。优秀的变幅系统设计以尽可能降低变幅机构的驱动功率和提高机构的操作性能为目的，臂架系统自重平衡的设计优劣是影响门及整体工作性能、安全性能的重要因素。

臂架系统自重平衡 Matlab 优化设计 UG Ansys

0 引 言

天津港第五港埠有限公司(以下简称“公司”)有4台门机在满载作业时均存在着不同程度的拉杆、冲杆现象，不能达到最大工作幅度。拉杆、冲杆，指的是起重机在进行变幅运动时臂架不能在变幅范围内平稳进行变幅运动，在变幅过程中的某点产生很大的冲击载荷，使臂架系统不能继续伸展。这会带来以下问题：①起重机在这种情况下按照原有变幅行程作业极有可能发生变幅齿条的损坏，乃至更严重的门机倾覆事故。②门机作业不能达到额定变幅，造成门机抓取范围缩小，需要大量机械辅助作业，加大作业成本。

本文以40～43,m门座式起重机为研究对象，对其进行臂架系统设计方案和理性分析，并以其结构尺寸为依据建立门座式起重机臂架系统的优化数学模型。利用Matlab优化工具箱对其进行优化求解，并根据优化结果设计可行的改造方案，然后利用UG软件对改造后的臂架系统进行三维建模，利用ANSYS软件对其关键部位进行静力学强度校核，以验证优化的效果。

1 门机臂架系统四连杆机构合理性分析

1.1 设计目标

40～43,m门机采用的臂架形式是四连杆组合形式，该形式的臂架系统设计目标为：①四连杆各部位长度合理，使吊重(货物)在变幅过程中运行轨迹趋近于平行于水平面的直线；②门机变幅时由货物产生的变幅阻力尽量小；③臂架系统各杆件、平衡系统以及货物对臂架下铰点产生力矩的矢量和尽量小，且在变幅过程中的某个位置达到力矩的平衡；④平衡重尽量小。

验证臂架四连杆机构设计的合理性首先要建立该系统的简化模型，列出各部位参数相互制约的关系式，验证四连杆机构的运动轨迹是否符合预期。

1.2 简化模型

门机四连杆组合臂架系统可以简化为如图1所示的以点O、O’、A、B为顶点的四连杆模型，而点A、B、C组成的三角形刚性梁结构即为象鼻梁的简化形式，臂架四连杆机构的杆件尺寸的设计合理性首先要验证象鼻梁端点在变幅行程内的运动轨迹，也就是C点的轨迹是否接近一条水平直线。

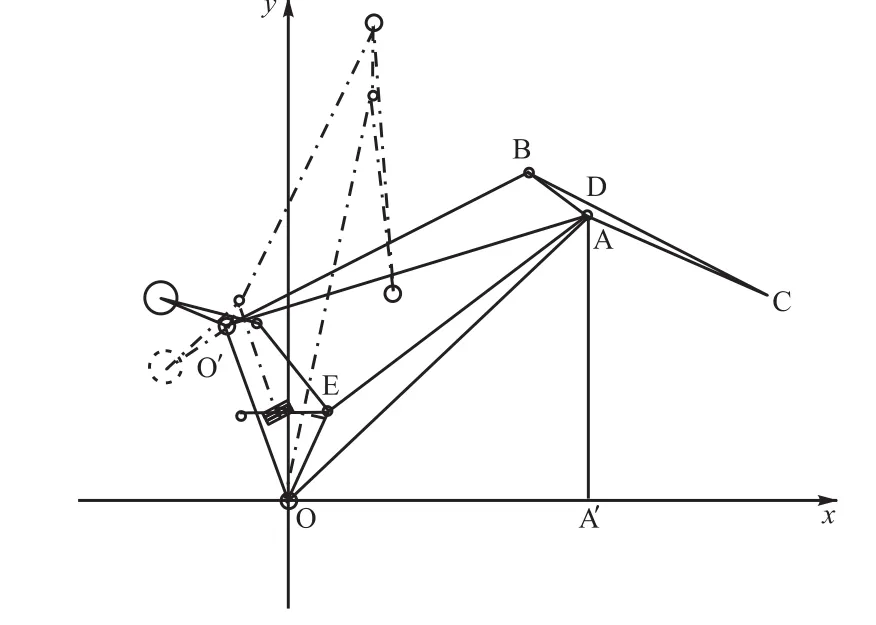
图1 臂架系统四连杆简化模型Fig.1 Simplified model of luffing system’s four-bar linkage

1.3 象鼻梁端点轨迹计算

为了方便计算，首先将臂架四连杆相关的尺寸参数用字母表示，如图2所示：

图2 臂架四连杆Fig.2 Luffing system’s four-bar linkage

另外，令θ1=∠ABC ；θ2=∠AOA′；θ3=∠ACC′；θ4=∠EOA ；θ5=∠O1OE；θ6=∠O1AB ；θ7=∠EAO；θ8=∠O1AE ；θ9=∠OAA′；θ10=∠CAA′。

则在最大幅度时有：

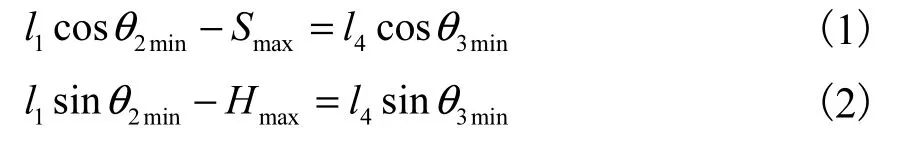
将两式分别平方并求和得：

展开并整理得：

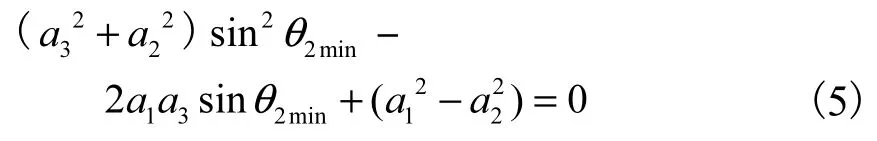
解此一元二次方程可得最大幅度时主臂架摆角：

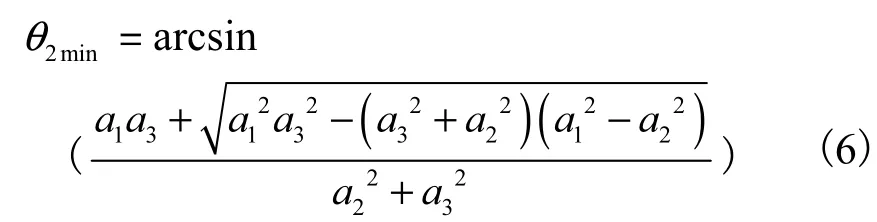
同理可求得最小幅度时主臂架摆角：

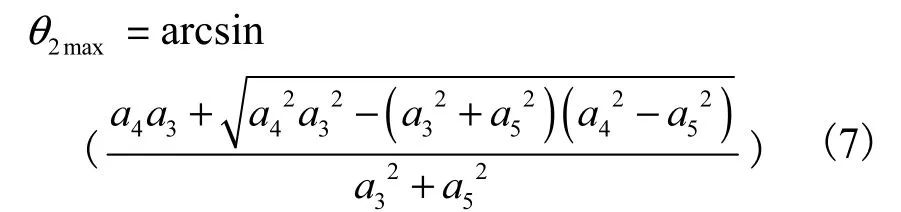
以主臂架摆角θ2作为自变量，θ2min到θ2max是其变化范围，则有：

利用MATLAB软件的绘图功能可以绘制出点C(Xc，Yc)的曲线。编写程序需要的相关数值根据几何关系可计算如下：

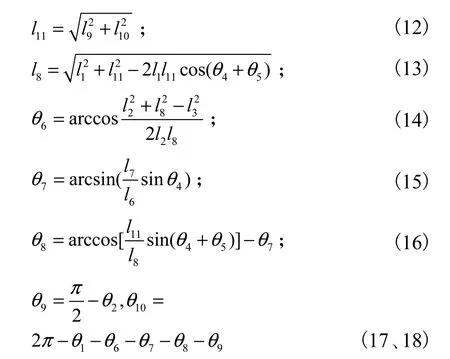
带入已知40～43,m门机的臂架系统参数，在Matlab中编写绘图函数M文件(部分)如下：得到C点轨迹图如图3。

图3 象鼻梁端点运动轨迹Fig.3 The trajectory of Trunk beam end point

由图3可以看出，Yc在整个变幅过程中虽然变化值不是很大，但在接近最大变幅时曲线上扬有一个明显拐点，这很可能就是臂架变幅在接近最大时发生失稳的重要原因。

1.4 臂架失稳原因的确定

为进一步确定臂架在变幅过程中失稳的原因，我们采用力矩检测工具对门机变幅过程中变幅系统减速器高速轴的力矩进行了测量，得到结果如表1所示：

表1 变幅系统减速器高速轴扭矩测量结果Tab.1 Torque measurement results of high speed shaft of reducer

在门机变幅系统的设计中，臂架进行变幅运动时应存在一个力矩平衡点，即力矩零点，而由表1可以看出在整个变幅过程中减速器高速轴的扭矩方向始终没有变化(数值始终为负)，因此在变幅过程中不存在扭矩为零的变幅平衡点。这一点导致了门机臂架进行变幅的过程中稳定性不佳，进而不能达到最大幅度的结果。

2 门机臂架及平衡系统优化数学模型的建立

门机臂架及平衡系统的优化数学模型包括3个要素，即：设计变量、目标函数和约束条件。

2.1 设计变量的确定

以上文建立的臂架四连杆简化模型为基础，添加上平衡系统的相关参数，即构成了臂架及平衡系统的整体简化模型(见图4)。

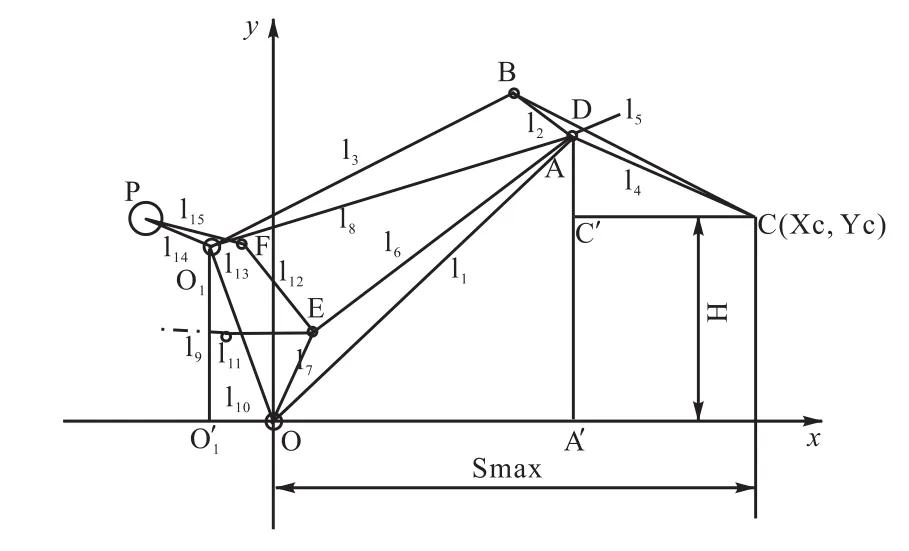
图4 门机臂架平衡系统优化设计变量Fig.4Designed variables of crane boom balance system optimization

如图4所示，由于点O和O1位置固定，则l9，l10，l11的长度固定，l5的值一般也取为常量，这里不做改变，需要优化的参数包括：

l1——主臂架的长度；l2——象鼻梁后臂长度；l3——大拉杆长度；l4——象鼻梁前臂长度；l6——象鼻梁铰点与小拉杆下铰点距离；l7——主臂架下铰点到小拉杆下铰点距离；l12——小拉杆长度；l13——平衡梁前臂长度；l14——平衡梁后臂长度；l15——配重中心点到小拉杆上铰点距离；Gp——配重重量。

这其中l14平衡梁后臂长度由于受到机房位置尺寸的影响不宜变动，因此也不做变化。

由此就得到了臂架及平衡系统的10个设计变量，用向量表示为：

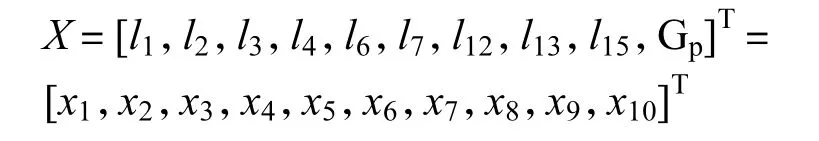
根据经验值，设定设计变量上限：

lb＝[30；4；24；10；20；5；6；1；6；45,000]；

设定变量上限为：

Ub＝[40，8；35；20；30；10；12；5；13；55,000]。

2.2 目标函数的确定

2.2.1 象鼻梁端点运动轨迹

根据1.3的具体运算，得到象鼻梁端点坐标函数方程：

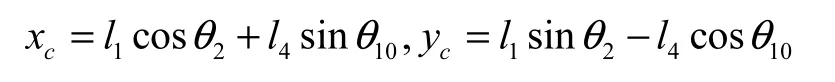
在xc在最大幅度与最小幅度之间变化时，yc应该接近于yc=H的一条直线，则目标函数可表示为：

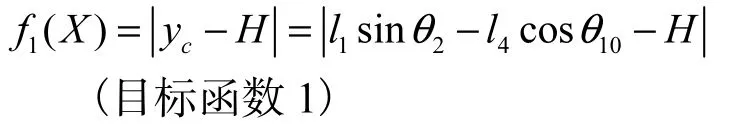
2.2.2 变幅阻力矩

臂架的变幅阻力矩可以利用象鼻梁端点C轨迹表达式并根据功能原理进行计算。设臂架从位置一摆动到位置二时臂架与水平面夹角θ2角变化值为Δθ2，象鼻梁端点C轨迹的高度变化为Δyc，负载货物重量为Q。则C点为取得克服货物重力升高Δyc所需的能量，需在臂架上作用力矩ΔM，且有：

ΔM×Δθ2=Q ×Δyc

由此得：

因此当臂架摆角幅度足够小时，每相邻两个幅度位置的象鼻梁端点高度差值为单位重量货物所引起的在该微量摆角行程上的臂架力矩。

2.2.3 臂架平衡系统不平衡力矩

若将臂架平衡系统中各杆件设为均质等截面杆件，则平衡系统重量可表示为：

式中：1η为主臂架长度重量，2η为象鼻梁长度重量，3η为大拉杆长度重量，4η为平衡系统长度重量。

对于本文引用的40～43,m门机，其长度重量计算如表2。

表2 臂架平衡系统长度重量计算Tab.2 Boom balance system length weight calculation

定义了长度重量后，整个臂架平衡系统则完全简化为有长度、有重量，无宽度、无高度的杆件系统模型。由于在变幅过程中主臂架下铰点O为臂架系统的回转中心，根据瞬心回转功率法，可以计算各杆件自重对O点的力矩。

对重应与臂架重力、象鼻梁重力，以及拉杆重力的一半(如不计杠杆系统自重重力)相平衡。

2.2.3.1 象鼻梁自重力矩Mxbl

由于整个象鼻梁长度和为l2+l4，而长度重量的定义把所有杆件设为均质杆件，则重心位置应位于处，即BC上位于B点处。

则象鼻梁对主臂架下铰点O的力矩为：

式中：Gxbl=η2(l2+l4)——象鼻梁自重(kg)。

2.2.3.2 大拉杆自重力矩Mdlg

设大拉杆自重的一半Gdlg作用在 F 点，则：

2.2.3.3 主臂架自重力矩Mzbj

式中：Gzbj=η1l1——主臂架自重(kg)。

2.2.3.4 平衡系统自重力矩Mph

设平衡重系统(包括配重、平衡梁、小拉杆)的合成中心在P点，则：

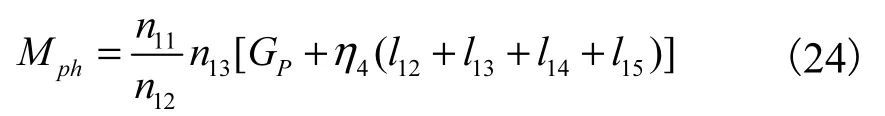
式中：GP——平衡重重量。

2.2.3.5 系统不平衡力矩

臂架系统自重力矩为主臂架、象鼻梁、大拉杆及变幅齿条自重力矩之和，即：

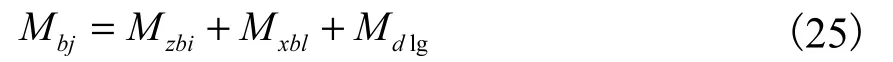
整个臂架及平衡系统的不平衡力矩为臂架系统力矩与平衡系统力矩之差，即为：

2.2.4 配重重量

在满足平衡条件的情况下，配重的重量应该取尽量小的值，因此：

f3(X)＝Gp(目标函数3)

其中，Gp为配重重量。

2.3 约束条件的确定

在臂架平衡系统的设计中，约束限制主要包括结构布局方面的限制、设计准则要求限制、经验数据限定的变量范围等方面，约束条件的限定既可以避免计算过程中可能发生的超界溢出现象，又可以提高优化搜索速度，在优化设计的过程中具有相当重要的作用。本文根据以下几个方面制定优化约束条件：

2.3.1 象鼻梁前后臂的长度比

象鼻梁的前后臂的比值根据起重机设计手册为：象鼻梁前臂长度为后臂的0.3～0.5倍，即：

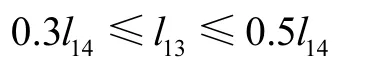
这里可表现为两个约束关系式：

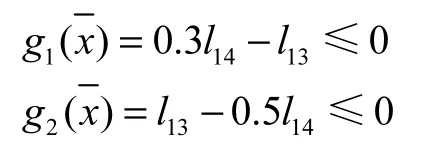
2.3.2 臂架与水平面夹角

臂架于水平面的夹角根据经验数据其变化范围在30～80 °之间，即：

这里也需要两个约束表达式：

2.3.3 象鼻梁与水平线夹角

象鼻梁同水平线之间的夹角变动范围在8～90,°之间，即：

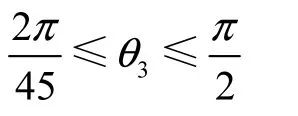
用约束表达式可以表达为：

2.3.4 臂架系统四连杆机构约束

即：

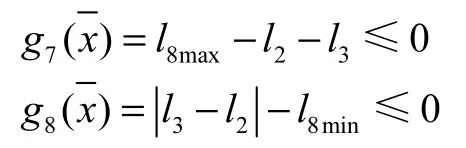
2.3.5 平衡系统四连杆机构约束

2.3.6 铰点E的设计

即：

2.3.7 平衡量前后臂夹角

由于平衡梁后臂应该设计得尽量长，所以平衡梁前后臂夹角应为钝角，设平衡量前后臂夹角为θ11，即有：

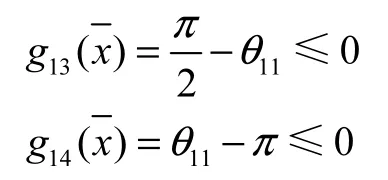
还有，应要求臂架处于最小幅度时，平衡重不与机房碰撞。设平衡梁后臂与竖直线夹角为θ12，即：

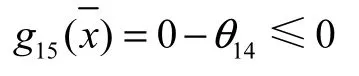
2.3.8 臂架不平衡力矩

在最大、最小幅度时，臂架系统的不平衡力矩应有利于臂架恢复正常位置。若设载荷对主臂下铰点O 引起的力矩有使臂架系统向大幅度方向运动的趋势为正，有向小幅度方向运动的趋势为负，则在最大幅度时，臂架系统不平衡力矩应为负，在最小幅度时，臂架系统不平衡力矩应为正，则有约束：

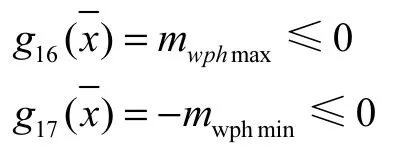
式中：mwphmax、mwphmin分别为载荷在最大幅度，最小幅度时的杆件自重不平衡力矩。

此外，根据起重机设计手册，臂架平衡系统不平衡力矩应小于臂架四连杆对O点力矩之和的十分之一，则有：

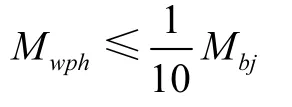
写成约束函数则为：

3 臂架及平衡系统的优化

3.1 目标函数f文件的编写

根据上文对优化目标的定义，一共有3个目标函数，将目标函数f文件命名为BJPH_3,mb_MB．m，编写程序如下(部分)：

function f＝BJPH_3,mb_MB(x)

Smin＝8.76；Smax＝39.743；H＝16.87；l5＝0.854；l9＝14.4；l10＝5；l14＝0.6；已知条件定义(最小、最大幅值；起升高度；象鼻梁铰点偏移距离；主臂架下铰点与大拉杆下铰点水平、竖直距离；象鼻梁后臂距离)。

a1＝x(1).^2＋Smax.^2＋H.^2－x(4).^2；

a2＝2.*x(1).*Smax；

a3＝2.*x(1).*H；

……

f(1)＝abs(yc－H)；%,目标函数1

f(2)＝Mbj－Mph；%,目标函数2

f(3)＝x(10)；%,目标函数3

3.2 约束条件M文件的编写

根据上文对约束条件的定义，将目标函数M文件命名为BJPH_3,mb_YS．m，编写程序如下(部分)：function[g，ceq]＝BJPH_3,mb_YS(x)

l14＝0.6；%,已知条件象鼻梁后臂长度

Smin＝12；Smax＝48；H＝16.87；L5＝0.854；

l9＝14.4；L10＝5；

a1＝x(1).^2＋Smax.^2＋H.^2-x(4).^2；

……

g(16)＝Mbjmax-Mphmax；

g(17)＝Mphmin-Mbjmin；

g(18)＝Mbj-Mph-0.1.*Mbj；

ceq＝[]；

3.3 优化函数的调用及优化结果

调用优化工具箱的fgoalattain函数需要首先进入MATLAB软件主页面，开启优化工具箱后在弹出的优化工具箱界面中选择优化函数以及设定基本参数，优化结果显示(部分)：

x＝1.0,e＋04 *

0.003 ,4－0.000,0,i

0.000 ,6＋0.000,0,i

0.002 ,8

……

0.000 ,9

0.000 ,3

0.000 ,8

5.300 ,0＋0.000,0,i

fval＝

1.0 ,e＋04 *

0 0 5.300,0＋0.000,0,i

根据MATLAB计算结果，40～43,m门座式起重机优化前后相关参数变化如表3。

表3 优化参数比较表Tab.3 Comparison of optimization parameters

4 优化后模型的三维建模及静力分析

4.1 三维模型建立

根据优化设计结果，在调整主臂架、象鼻梁前后臂、大拉杆及小拉杆的长度后，在UG中建模如图5～9。

图5 主臂架三维模型Fig.5 3D model of the main arm

图6 象鼻梁三维模型Fig.6 3D model of the Trunk beam

图7 大拉杆三维模型Fig.7 3D model of the big draw rod

图8 小拉杆三维模型Fig.8 3D model of the small draw rod

图9 平衡梁三维模型Fig.9 3D model of the balance beam

根据各杆件在各自铰点上相连接的相互约束的条件，将主臂架、象鼻梁、大拉杆进行装配，并设计一部件代替门机机身主体，将其设为固定杆件，则主臂架可以绕主臂架下铰点和大拉杆下铰点作变幅运动。臂架系统装配模型如图10。

图10 臂架系统装配模型Fig.10 3D model of the arm rack system assembly

4.2 平衡系统的ANSYS有限元分析

将UG中建立的平衡梁三维模型导入ANSYS，在ANSYS中进行参数设置以及网格划分。

模型的工程单位、单元类型和材料性质设置如下：

工程单位，长度，mm；

质量，kg；

重量，N；

单元类型，二节点的三维梁单元；

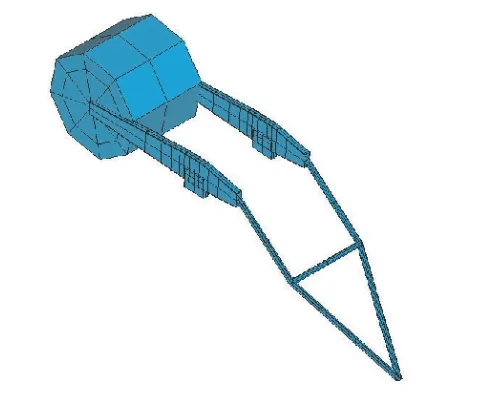
图11 平衡梁及小拉杆有限元模型Fig.11 Finite element modle of balance beam and small draw rod

材料性质，杨氏弹性模量 E＝2.06,e＋5,MPa；

泊松比µ＝0.3；

建立完成的平衡梁有限元模型如图11所示。

4.2.1 主要载荷

由结构自重引起的载荷SG。

4.2.2 静力计算结果

下面分别给出结构增加活配重前后平衡梁、小拉杆应力计算结果表4所示：

表4 1类工况应力计算结果Tab.4Stress calculation results of Category 1 working conditions

由表4可以看出，小拉杆结构应力增加15.921,MPa，平衡梁结构应力增加20.132,MPa，其所受应力云图见图12、13。

图12 平衡梁应力云图Fig.12 Stress cloud of balance beam

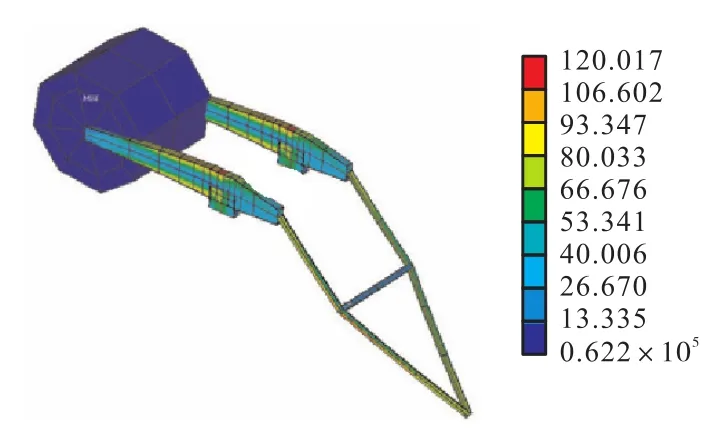
图13 小拉杆应力云图Fig.13 Stress cloud of small draw rod

4.2.3 弹性极限评估

在结构中，所用到的材料为Q235C，其机械性能如下：

弹性极限 σE＝235,MPa

1、2、3类工况的许用应力σα如下：

1类工况σα1＝σE/1.5＝156.7,MPa

2类工况σα2＝σE/1.33＝176.7,MPa

综上所述，该平衡系统在优化之后结构仍满足静力强度的要求。

5 平衡系统改造

根据表3比价系统杆件长度变化量相对于初始长度变化幅度很小，而配重重量变化幅度较大，可见该门机逼架平衡系统的主要问题在于配重不足。考虑到臂架系统改造难度大、成本高，最终决定仅对平衡系统进行改造。其方案是：增加的后配重为两个圆柱形箱体，焊接于原配重两侧，以增加配重重量。改造后的优点为：①提高门机的抓取范围，减少下舱机械的辅助作业时间，降低作业成本；②变幅系统整体载荷状况改善，降低了便服系统故障频次级门及维修成本。■

［1］ 刘剑波. 单臂架门座式起重机臂架变幅系统的优化设计[D]. 上海：上海交通大学，2011.

［2］ 孙翔. 门座式起重机臂架四连杆结构设计[J]. 工程技术：引文版，2016(5)：248.

［3］ 黄陈娣. 浅析门座式起重机臂架系统的优化设计[J].科技促进发展，2012(5)：128-130.

Optimized Study of Portal Crane’s Boom and Dead Load Blanced System

CAO Na
(Tianjin Port No.5 Stevedoring Co.，Ltd.，Tianjin 300456，China)

Along with the development of economy and the prosperity of international logistics industry，efficiency，safety and reliability of port logistics portal crane regarding loading and unloading of goods are facing higher requirements．Therefore，research on various aspects of portal crane has become a hot topic both at home and abroad．Luffing system of four connecting rod hinge arm is the most widely used form of portal crane jib．The portal crane is used to change the amplitude of the agency．The design of the luffing system to reduce the driving power of luffing mechanism and improve the operating performance of institutions is an important factor affecting the performance of the door and the whole work and safety performance.

self balance arm frame system；Metlab；optimization design；UG；Ansys

TH21

：A

：1006-8945(2016)10-0062-08

2016-09-02