1995
—2012年国内个人收入分布函数演化研究
高 立, 周延杰,王 浩
(西安财经学院 a.信息学院;b.商学院,陕西 西安 710100)
1995
高立a, 周延杰a,王浩b
(西安财经学院 a.信息学院;b.商学院,陕西 西安 710100)
摘要:基于国家统计局1995―2012年个人人均年收入数据,运用数据拟合方法,研究国内绝大多数个人人均年收入的累积分布函数和概率密度函数从1995—2012年的演化过程,结果显示:累积分布函数为,遵循高斯分布;概率密度函数为,概率密度函数图像的宽度随着时间的推移从1995—2012年逐步变宽,是(x-μ)因子推动概率密度函数P(x)中的部分,在使图像逐步变宽的同时右方出现了一个逐年加长的类似指数函数的长尾,这种图像提示从1995—2012年极少数人获取了极大数量的个人收入;进一步利用个人人均年收入的概率密度函数P(x)计算相应的Gini系数在这一时期的演化后发现,当今中国收入不公平性已很严重,各级相关部门应当从政策改革和福利分配方面有所重视。
关键词:经济物理学;累积分布函数;概率密度函数;基尼系数
一、引言
经济物理学(Econophysics)是近十几年来新兴的运用统计物理的思想、概念和模型定量研究经济问题的前沿交叉学科[1]5-7,研究内容涉及收入分布、国民财富、金融市场的波动特性和人口经济等诸多领域。1995年,美国科学院院士Stanley等人第一次使用经济物理学一词为这一新的交叉学科命名。目前,经济物理学已成为复杂性研究领域中的一个重要分支,为经济学家在研究复杂经济系统时提供了全新的工具和模型,而且许多模型已广泛用于分析和刻画个人收入、个人消费和个人财富分布,其中利用经济物理学对个人收入分布的研究已在澳大利亚、巴西、印度、意大利、日本、法国和德国、英国和美国广泛开展[2-9]。然而,目前因为诸多原因,系统性探求中国居民收入分布函数的研究较少,故对于中国居民个人收入的累积分布函数和概率密度函数的演化过程的研究尤为迫切。在类似和相关的研究中,张萌旭等人对2005—2010年安徽省城镇居民收入分布函数进行了研究[10];陈云在研究居民收入分布核密度基础上,认为中国居民收入水平在总体提高的同时加剧了居民收入分布的分化程度[11];许研等人利用国家统计局1998—2002年家庭收入计划的数据,得出其分布函数为对数正态分布加幂律分布长尾的结论[12]。综合来看,国内至今仍然缺乏一种系统性的个人收入长期演化过程的研究,从探索中国经济可持续发展的角度而言,对个人收入长期演化过程进行研究具有重大的经济和政治意义。
中国是世界上人口最多的国家,改革开放以来经济持续快速增长并取得了令世人瞩目的成就,但同时经济发展的不平等性也日益突出,其中个人收入分配问题一直是全社会关注的焦点。个人收入分布函数的动力学研究,不但可以为探讨如何缩小收入差距、脱贫解困以及收入再分配等一系列课题提供科学的决策依据,而且还可总结出中国经济发展不平等性产生的原因以及如何制定相应的方针政策缓解经济发展不平等性带来的社会矛盾和压力,并为中国经济可持续发展做出贡献。
二、概率密度函数分析
收入分布变量x由概率密度函数(PDF)P(x)来刻画,即在x到x+dx区间发现收入为x的概率为P(x)dx。因此,概率密度函数的研究就成为了个人收入研究的关键,本文首先对几种较具代表性的个人收入概率密度函数进行分析。
Drăgulescu、Richmond、Yakovenko通过对英国和美国的个人收入概率密度函数的演化研究,发现这两个国家个人收入的概率密度函数对于绝大多数人来说遵循指数函数分布,收入极高的极少数人则遵循幂律分布[13-14];Ferrero和Chakraborti等人在研究日本和新西兰等国家的个人收入的基础上加以模拟计算的方法,得出了另一种个人收入的概率密度函数呈现Gamma函数的结论[15-16; 在中国也有相应的成果,许研等人是中国较为系统研究个人收入概率密度函数的学者,他们利用国家统计局1998—2002年家庭收入计划的数据,并且与Gamma函数进行对比研究发现,中国个人收入概率密度函数绝大多数人符合对数正态分布,极少数高收入者遵循幂律分布。
综上所述,本文简要地将刻画个人收入的概率密度函数总结为以下几种函数形式:
(1)
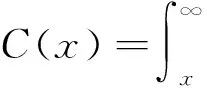
(2)

与本研究最为接近的是许研等人的研究[12],其研究从时间跨度上应当属于中国经济发展的某一个特定阶段。本文希望通过得到中国个人收入的概率密度函数在一个较长时间的演化规律,并与以上典型的分布函数进行比较后希望有所发现,具体方法是根据国家统计局1995—2012年数据,画出此期间个人收入的散点图[17];再利用Origin 8.0对散点图进行拟合,得出个人收入的累积分布函数;最后进行分析计算,得出中国个人收入的概率密度分布函数的演化过程,并对其进行深入探讨。
三、数据拟合结果分析
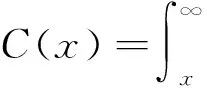
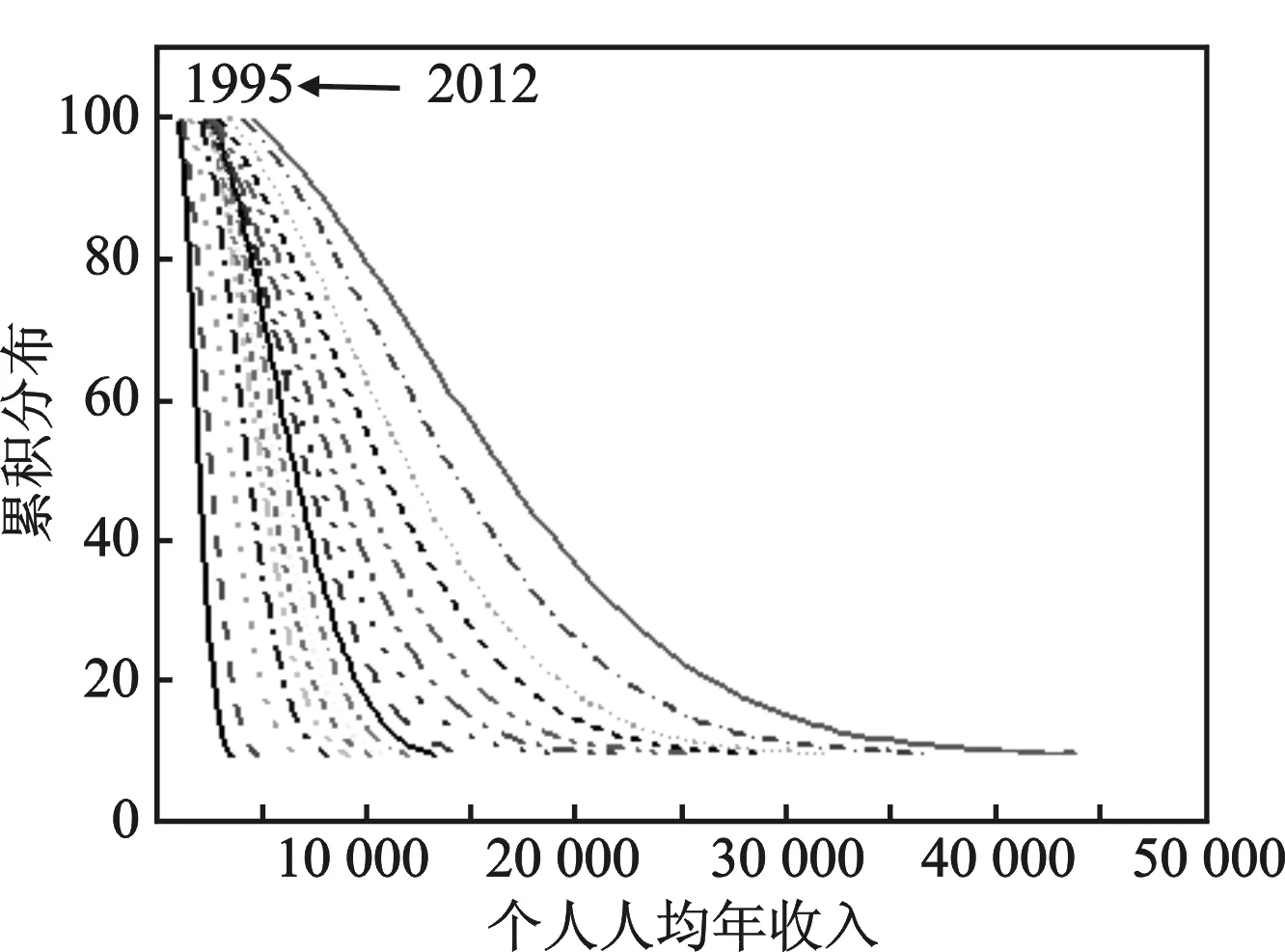
图1 1995—2012年国内个人人均收入累积分布函数图
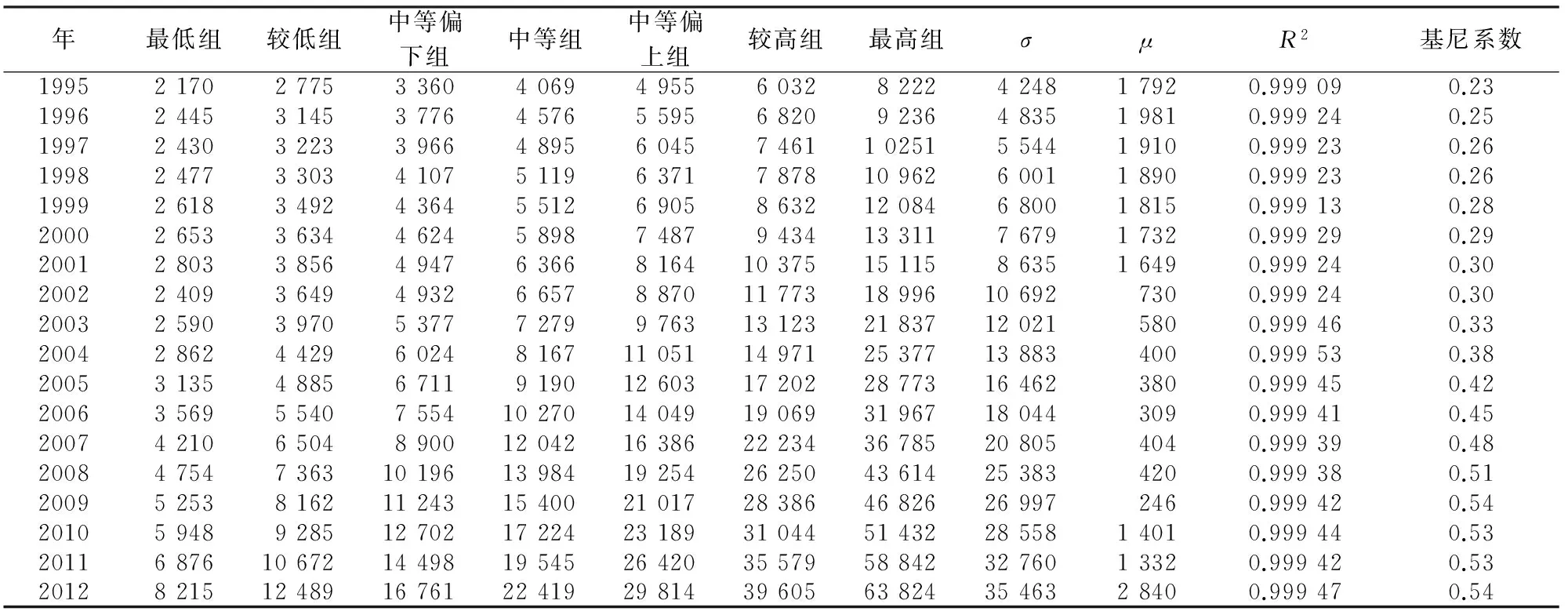
单位: 元
注:数据来源于《中国统计年鉴》。

图21995—2012年国内个人图31995―2012年国内个人人均收入累积分布函数
人均收入归一化后比较图高斯拟合与对数正态分布拟合比较图
四、研究结果与建议

本文经过拟合国内个人人均收入的数据发现,国内个人人均收入累积分布函数为高斯函数:
(3)
其中A为常数, σ2为均方差,μ为均值(见表1)。需要说明一点,在理论上,应当满足0≤x≤μ条件,但是在现实社会中存在负债的情形,也就是说存在x≤0这种情形,当然在正常运行的社会中这一人群数量很少。由于本文研究的是绝大多数个人收入,因此不考虑x≤0这种情形,故利用累积分布函数得出国内个人人均收入的概率密度函数(PDF)为:
(4)
(5)
当x≥μ时,生存函数为:
(6)
当x<μ时,生存函数为S(x)=1。

(7)
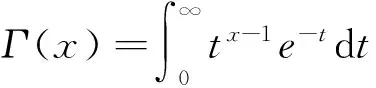
(8)
(9)
对本研究得出的国内个人人均收入的概率密度函数(PDF)方程(4)做进一步的统计学分析研究,同时还可以将这一函数看作是一个不同权重分布的函数形式:
(10)
其中f(x)可以看作标准高斯分布,参数为(μ;σ);w(x)为权重分布函数,在本研究中可以定义为:当x≥μ时w(x)=(x-μ);当x<μ时w(x)=0,而新的函数fw(x)是关于变量X和权重分布函数w(x)相关的概率密度函数(PDF)。在本研究中,由于w(x)=(x-μ)与fw(x)是线性关系,被称为长度或者大小偏移函数形式,因此这类研究属于对于长度或者大小偏移的抽样研究。以研究收入分布为例,fw(x)这个函数提供了不同收入的不同权重信息。
从经济物理学角度研究,则体现出了一个非常有趣的解释:收入的概率密度函数是因子(x-μ)与高斯分布函数的乘积,也就是说(x-μ)因子造成了对称的高斯函数的偏移(见图4),同时也可视之为概率密度函数图像的宽度随着时间的推移从1995—2012年逐步变宽的潜在原因,这一概率密度函数表达形式是首次被提出的。中国经济自从改革开放以来变化巨大,这种巨变自然反映在许多经济学统计数据中,比如个人收入和个人财富分布的演化规律中,而从经济物理学角度对本文的研究结果进行动力学分析,正是(x-μ)因子,即高收入与收入均值的差异造成了国内个人收入概率密度函数的偏移和长尾的出现,也恰恰就是邓小平所说的“让少数人先富起来”带来的竞争机制。在中国完全计划经济时期,个人收入几乎呈现高斯分布,但是一旦引入竞争机制以后,就会出现统计学的“吸引子”[1]27-28,即个人收入分布向帕累托分布演化,由此得出结论为中国目前经济运行过程中个人收入分布是总体演化过程的中间状态。中国改革开放以后,在引入竞争机制的同时,贫富差异相伴而生,个人收入概率密度函数图像中的长尾逐步演化而成,概率密度函数图像的宽度随着时间的推移从1995—2012年逐步变宽也反映了这一现象。利用洛伦兹曲线,计算出了1995—2012年国内个人收入的基尼系数[19],结果表明从1995—2012年,基尼系数呈现增加的趋势(见表1),为简明仅列出1995年、2005年、2012年的洛伦兹曲线(见图5),其中1995年、2005年、2012年的基尼系数分别为0.23、0.42和0.54,说明从个人收入演变的过程来看,中国的不平等性正在加剧。
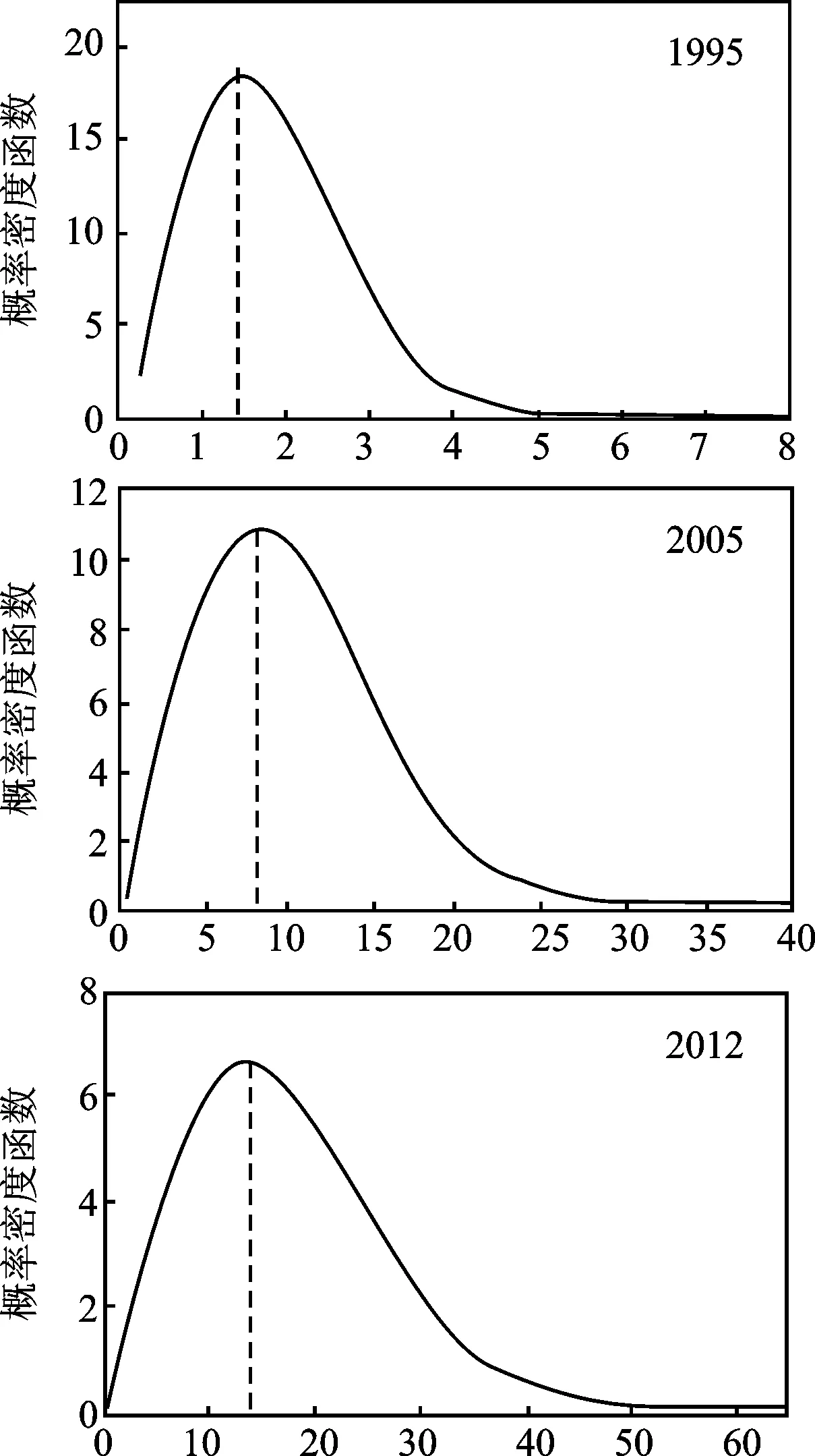
图4 1995年、2005年、2012年个人收入概率密度分布函数图
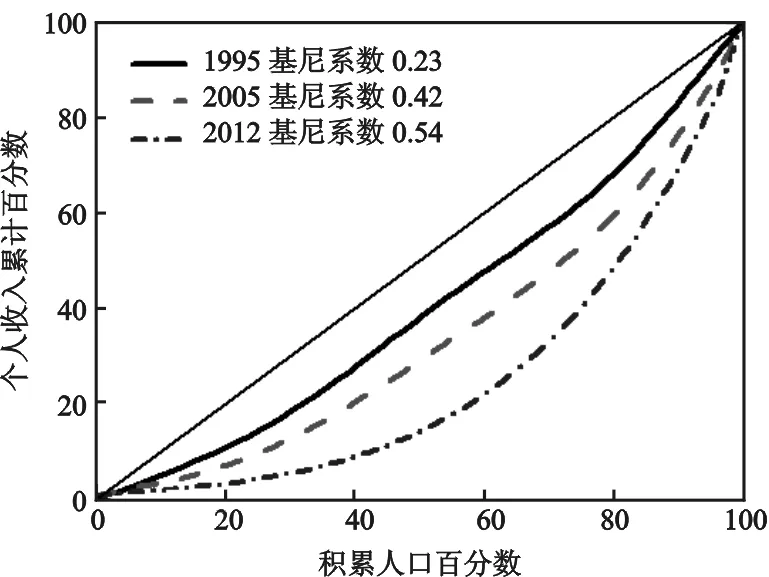
图5 1995年、2005年、2012年个人收入洛伦兹曲线以及相应的基尼系数图
当前,中国正经历着一场划时代的社会变迁,这个巨大变化具体反映在以下几个方面:其一,总体上经济高速度发展;其二,制度方面,中国正经历着从计划经济向市场经济更深层次的改革和转型;其三,社会主义的许多特征,比如城市居民由国家和单位安排住房和工作等,在今天的中国已经发生了根本性的变化;其四,人口数量以及人口年龄结构和行业的分布变化已成为研究中国社会和经济的一个重要因素。上述这些变化都在影响着当今中国人的生活和工作,同时也影响着中国社会的不平等性,现阶段中国收入不平等是一个不容否认的事实,这也是中国经济快速发展的必然结果。从本文的研究结果看,竞争的经济系统在带来经济竞争活力的同时,也衍生出了不平等的问题,因此从本研究的结论出发,提出以下建议:
第一,从1995—2012年国内个人收入概率密度函数演化过程来看,尽管整体的个人收入增加很快,但是高收入人群与中、低收入者之间的收入差距有扩大的趋势,这一现象影响着广大民众对中国社会不平等性的认识,相关部门对此应有充分了解和认识。
第二,快速增加的长尾现象和基尼系数的演化过程可以肯定中国社会的不平等性正处于快速发展的阶段,此时应当特别关注低收入家庭的社会保障问题,尤其是当前教育、医疗保障体制处于仍远未完善的经济发展阶段,而关注低收入家庭的社会保障问题则是关注社会稳定发展的问题。
第三,从1995—2012年国内个人收入概率密度函数演化曲线中应当更清晰地认识到,如果想进一步提高中、低收入者的收入水平,将比改革发展初期难度更大,因为越往PDF分布曲线的右边,同样的面积则意味着需要更大的资金量作支撑。特别是随着经济的发展,国家对劳动者技能的培训、针对特殊人群社会福利的完善以及对新行业和新就业岗位的挖掘等方面,还需要做大量和长期的工作。
参考文献:
[1]Mantegna R, Stanley H E. An Introduction to Econophysics: Correlations in Finance[M]. Gambridge:Cambridge University Press, 2000.
[2]Banerjee A, Yakovenko V M, Matteo T Di. A Study of the Personal Income Distribution in Australia[J]. Physica A, 2006,370.
[3]Cowell F A, Ferreira F H G, Litchfeld J A.Income Distribution in Brazil 1981-1990. Parametric and Non-Parametric Approaches[J]. Income Distribution 1998,8(1).
[4]Sinha S. Evidence for Power-Law Tail of the Wealth Distribution in India[J]. Physica A, 2006,359.
[5]Clementi F, Gallegati M. Power Law Tails in the Italian Personal Income Distribution[J]. Physica A, 2005,350.
[6]Aoyama H, Souma W, Nagahara Y, Okazaki M P, Takayasu H, Takayasu N. Pareto's Law for Income of Individuals and Debt of Bankrupt Companies[J]. Fractals 2000,8.
[7]Quintano C, D’Agostino A. Studying Inequality in Income Distribution of Single-Person Households in Four Developed Countries[J]. Rev. Income Wealth 2006,52.
[8]Harrison A. Earnings by size: A Tale of Two Distributions[J]. The Review of Economic Studies, 1981,48.
[9]Yakovenko V M, Jr. Rosser J B. Colloquium:Statisticall Mechanics of Money, Money,Wealth, and Income[J]. Reviews of Modern Physics, 2009,81.
[10]张萌旭,陈建东,蒲明. 城镇居民收入分布函数的研究[J]. 数量经济技术经济研究, 2013(4).
[11]陈云. 中国居民收入分布专题实证研究[J]. 统计与信息论坛, 2013(2).
[12]Xu Y, Guo L P, Ding N, Wang Y G.Evidence of Scaling in Chinese Income Distribution[J]. Chinese Physics Letter, 2010,27(7).
[13]Drăgulescu A, Yakovenko V M.Exponential and Power-Law Probability Distributions of Wealth Income in the United Kingdom and the United States[J].Physica A, 2001,299.
[14]Richmond P,Pepetowicz P,Hutaler S,Coelho R. Comments on Recent Stadies of the Dynamics Distrbution of Money[J].Physica A,2006,370.
[15]Ferrero J C.The Statistical Distribution of Money and the Rate of Money Transference[J].Physica A,2004,341.
[16]Chakraborti A, Patriarca M.Gamma-Distribution and Wealth Inequality[J].Pramana-Journal of Physics,2008,71.
[17]国家统计局.中国统计年鉴[EB/OL]. http://www.stats.gov.cn/tjsj/ndsj.
[18]Boghosian B. Fokker-Planck Description of Wealth Dynamics and the Origin of Pareto's Law[J]. International Journal of Modern Physics C,2014,25.
[19]张建华.一种简便易用的基尼系数计算方法[J].山西农业大学学报:社会科学版,2007, 6(3).
(责任编辑:郭诗梦)
Investigation on Evolution of Chinese Individuals' Income Distribution 1995-2012
GAO Lia, ZHOU Yan-jiea, WANG Haob
(a. School of Information; b. School of Business, Xi'an University of Finance and Economics, Xi'an 710100, China)
Abstract:Based on the survey data of per capita disposable income released by the National Bureau of Statistics of China (NBS), we fit the data and present a comprehensive study of the evolution of the majority population individual income distribution from 1995-2012. The cumulative distribution functions (CDFs) and probability density functions (PDFs) of China are presented. The whole CDFs follow Gauss function C(x) for the majority population individuals and the PDFs obey . The width of the PDF is wider and wider from 1995 to 2012, suggesting the factor (x-μ)push the right part of the curve to the righter and righter and it makes a long tail in the high income similar to exponential distribution from 1995 to 2012. This indicates very few people get extremely high income and it arises more and more inequality in China now results from our calculation of the evolution of the Gini coefficient from 1995 to 2012. Our conclusion suggests that reform of polices of income and proper polices for public welfare should be considered by the government.
Key words:econophysics; cumulative distribution function; probability density function; Gini coefficient
收稿日期:2015-07-20;修复日期:2015-12-11
基金项目:陕西省教育厅科研计划项目《基于经济物理学对社会不公平性的经济学参数的研究》(14JK1275)
作者简介:高立,男,陕西米脂人,物理学博士,讲师,研究方向:经济物理学;
中图分类号:O21∶F014.4
文献标志码:A
文章编号:1007-3116(2016)02-0008-06
周延杰,男,河北邢台人,硕士,副教授,研究方向:智能计算和系统优化,知识管理与web数据挖掘;
王浩,女,新疆乌鲁木齐人,医学博士,教授,研究方向:心理与行为。
【统计理论与方法】

