基于HyperSizer的复合材料舱门结构渐进式优化设计

李宇峰，贺高

(中国航空工业集团公司 第一飞机设计研究院，西安　710089)

基于HyperSizer的复合材料舱门结构渐进式优化设计

李宇峰，贺高

(中国航空工业集团公司 第一飞机设计研究院，西安710089)

摘要：结构重量是飞机复合材料结构设计需要考虑的重要因素和约束条件。针对某大型复合材料舱门设计方案，建立有限元模型，使用Patran/Nastran进行初步分析，再应用HyperSizer开展渐进式优化设计，优选出符合设计要求的方案，并计算构型的截面参数、铺层角度和铺层顺序等设计参数，完成结构建模和渐进式优化分析过程。结果表明：使用HyperSize进行渐进式优化设计，降低了结构的重量，达到了预期目标。

关键词：复合材料；舱门；渐进式优化；HyperSizer

0引言

复合材料具有重量轻、比强度高、比刚度大、耐疲劳性、耐腐蚀、可设计性等诸多优点。使用复合材料设计，能够减轻结构重量，有效提高产品性能和竞争力。复合材料具有可设计性，可以根据结构构型和载荷条件，将复合材料按照设计需求进行铺设，达到使用最少的材料就能满足设计要求的目的，最有效地发挥材料的作用。

工程中广泛使用复合材料板壳结构，例如飞机机翼和尾翼上的翼面壁板、整流罩、舱门等。板壳结构不仅指板件、曲壳，还包括由板或壳组成的薄壁构件，以及由薄壁构件组成的结构等广义的板壳结构[1]。飞机舱门结构中最大的结构单元是蒙皮和桁条，二者也是受力最严重的构件，承受着弯曲、扭转、剪切等主要载荷的作用。采用复合材料进行优化设计，使结构形式的选择、参数的设置与各部件的载荷传递相协调，有利于传递载荷和减轻重量。

复合材料加筋板结构优化设计问题的设计变量较多，包括连续变量和离散变量，且变量之间相互耦合，致使优化设计的难度较大，传统的数学规划法、准则法难以解决此类问题[2]。近年来，国内外对此开展了广泛研究。L.Berke等[3]利用人工神经网络来优化飞机翼面的结构布局。M.Blair等[4]将快速建模方法应用于翼面结构的布局优化设计。张铁亮等[5]采用试验设计建立代理模型的方法实现了加筋板的布局优化。R.Rikards等[6]将代理模型技术应用于加筋板结构的设计优化中。S.Nagendra等[7]应用改进的遗传算法对加筋板结构进行了优化设计。J.Fatemi等[8]、J.H.Kang等[9]也在加筋板结构设计优化中采用了遗传算法。L.Lanzi等[10]、李烁等[11]分别利用神经网络对复合材料帽型加筋板进行了优化。Liu Wenli等[12]提出了一种基于程序包VICONOPT的复合材料加筋板优化方法。赵群等[13]提出了一种基于压弯刚度的复合材料加筋板布局优化设计。吴莉莉等[14]提出了加筋板稳定性约束下的二级协同优化算法。卢秉贺等[15]应用Patran/Nastran和HyperSizer对复合材料后机身加筋结构形式进行选型分析。裘健全[16]提出了一种基于HyperSizer的复合材料结构渐进式设计方法，但未进行实例分析运算。

本文针对大型复合材料舱门结构，结合工程实例，采用Patran/Nastran与HyperSizer交互运算的方法，来实现对复合材料舱门的渐进式优化设计。

1优化方法

采用Patran/Nastran与HyperSizer交互设计，对舱门加筋壁板结构进行渐进式优化分析，该过程是一个由总体-局部-细节的过程。具体优化过程为：①运用Patran建立有限元模型，提交到Nastran计算，得到载荷的大小和分布，并输出单元内力；②将有限元模型和计算结果导入HyperSizer中，利用HyperSizer的构型模块建立多个构型及其相应的结构尺寸、复合材料铺层，形成构型的数据集合；③依次对每一个不同的构型进行刚度、强度和稳定性等失效模式的分析校核，全部结构区域需要进行所有载荷工况下的分析，统计其重量及失效模式的最小安全裕度值，筛选出安全裕度值为正的方案并按重量大小排序，重量最轻的方案即为最优的初步优化方案；④计算得到各优化区域的铺层百分比、铺层角度、铺层顺序、最小安全裕度、单位重量等参数，即当前载荷下最优的构型参数。在完成一轮优化后，由于有限元模型的单元属性已被修改，整体结构的刚度需重新分布、重新计算以获得新的单元力；⑤通过对壳元重新生成NASTRAN PSHELL和MAT2数据类型以及对梁元重新生成PBAR和MAT1数据类型，完成有限元模型的更新；⑥从FEA输出文件读取新的单元力，作为下一轮优化的依据；直到重量优化曲线收敛，安全裕度、刚度指标满足要求，即可认为优化结束。优化流程如图1所示。

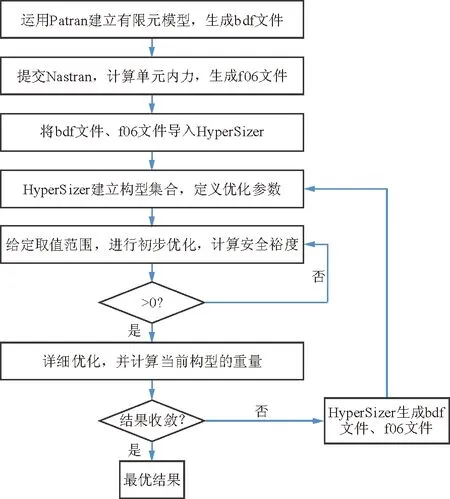
图1　优化流程图

1.1优化目标

最优构型即在相同的载荷作用下，满足刚度、强度、稳定性等约束准则，使结构的重量最轻。其通常模式表达为

MS.(φi)>0i=1,2,…,n

(1)

(2)

式中：φi为第i个构型的结构重量；MS为安全裕度。

1.2约束条件

(1) 霍夫曼(Hoffman)准则

式中：Xt为纵向拉伸强度；Xc为纵向压缩强度；Yt为横向拉伸强度；Yc为横向压缩强度；σ1、σ2为主方向应力；τ12为剪应力；S为剪切强度。

(2) 蔡-希尔(Tsai-Hill)准则

对于拉、压强度不同的材料，则对于拉应力，采用拉伸强度(X)；对于压应力，采用压缩强度(Y)。

(3) 蔡-胡(Tsai-Wu)失效准则

其中，

令

(3)

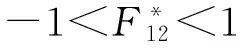
2优化模型

舱门位于机身下部，不参与全机受力，且位于气密区外，无气密要求。舱门所受载荷主要为气动载荷，故其需要具有足够的刚度，以保证在开启及关闭时不发生严重的变形。

舱门长为7.2 m，宽为1.3 m，由复合材料加筋壁板和六个铝合金支臂构成。支臂一端与铰链连接，连接处铰支；另一端通过连杆机构与旋转作动器连接，旋转作动器固支。舱门有限元模型如图2所示，复合材料加筋壁板根据支臂位置划分为七块优化设计区域。

图2　舱门有限元模型

载荷工况分别选取舱门关闭、打开时的气动载荷，均匀加载于壁板上：当舱门关闭时，P=3 800 N/m2；当舱门打开时，P=5 300 N/m2。

在计算分析时，对复合材料加筋壁板模型进行如下假设：①复合材料是线弹性的，无初始损伤；②壁板为板单元，初始模型蒙皮无筋条，为厚板；③支臂上缘、下缘为杆单元, 腹板为板单元。

金属材料属性和复合材料单向板属性分别如表1～表2所示。

表1　金属材料属性

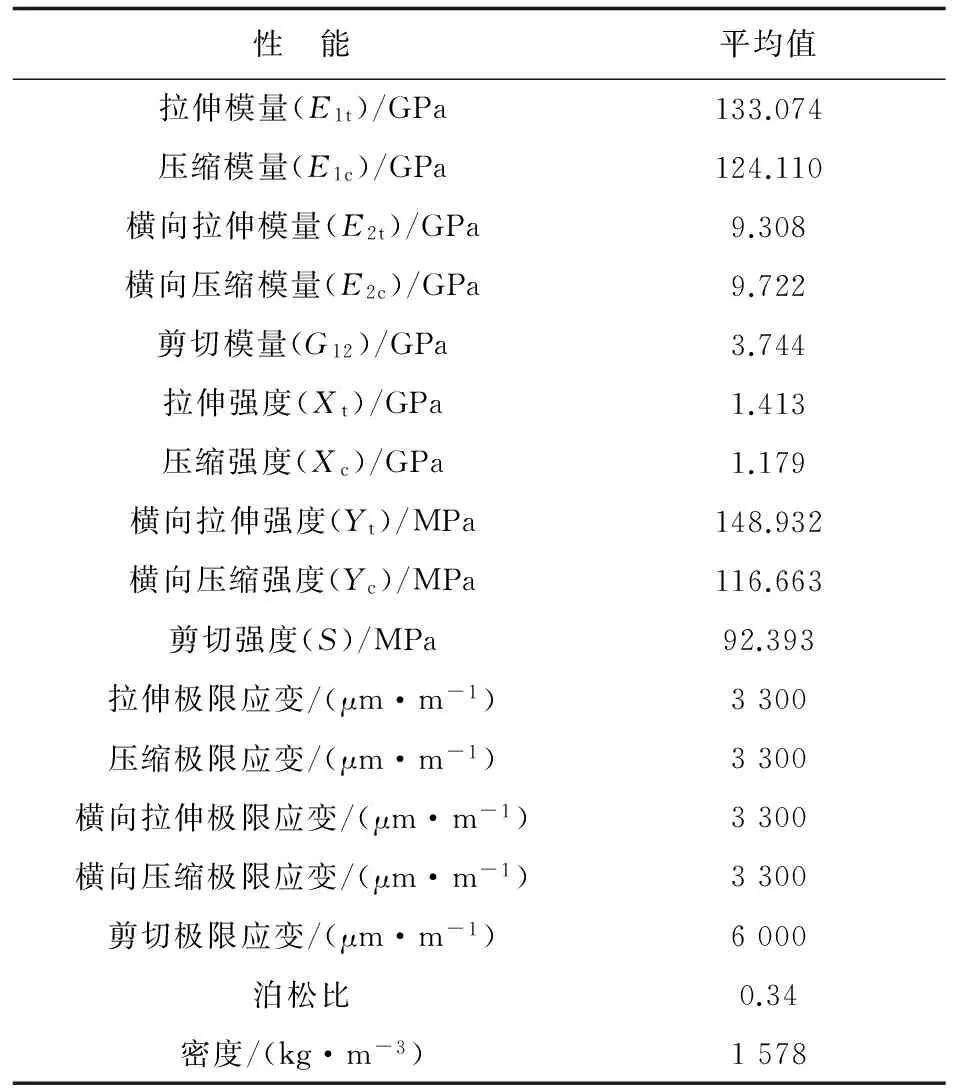
表2　复合材料单向板属性

3优化方案及结果

层压壁板常用的加筋切面形状主要有T型、J型、工字型以及帽型等。其中，帽型加筋由于切面尺寸较大且两边与蒙皮相连呈现出一个闭合切面(如图3所示)，使得在受压载荷条件下具有很高的承载能力。因此，本文选取帽型加筋作为层压结构优化设计截面，其几何参数S、ttf、tw、H、θ、Wt、Wb为优化设计变量，舱门在两种工况下的变形位移不超过5 mm为约束条件，使结构的整体质量最小作为最终的优化目标。

图3　帽型加筋切面示意图

限于篇幅，优化结果仅以图2中的区域2为例进行说明。根据受载情况分析，区域2所需蒙皮铺层的最佳厚度为2.23 mm，筋条铺层的最佳厚度为1.67 mm。加筋高度H=70 mm，间距S=300 mm，缘条宽度Wb=70 mm、Wt=60 mm，角度θ=65°，如表3所示。蒙皮的0°、±45°、90°铺层最佳比例为30%、60%、10%，筋条的0°、±45°、90°铺层最佳比例为40%、40%、20%。

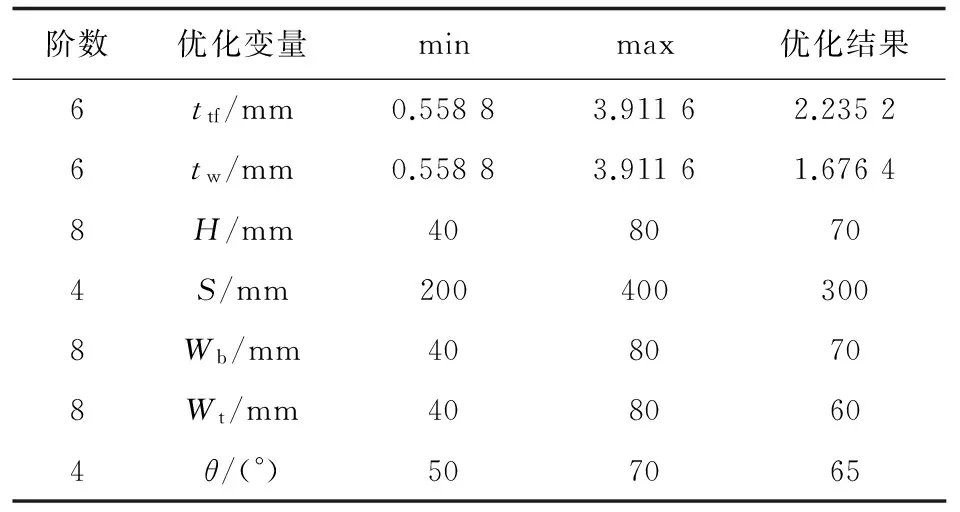
表3　优化区域2最终的铺层厚度及构型参数

通过HyperSizer计算、分析、调整，并反复迭代优化后，设计区域2最终的铺层设计为：蒙皮的铺层为11层，具体为[45/-45/0/45/-45/_90_]s；加筋的铺层为9层，具体为[45/-45/0/90/_0_]s。区域2在优化迭代过程中的变化规律如图4图所。

按舱门刚度要求，最大变形不超过5 mm。在全部设计区域进行渐进式交互优化后，与单用Patran/Nastran优化对比，如表4所示，可以看出渐进式交互优化后的结构重量略轻一些。

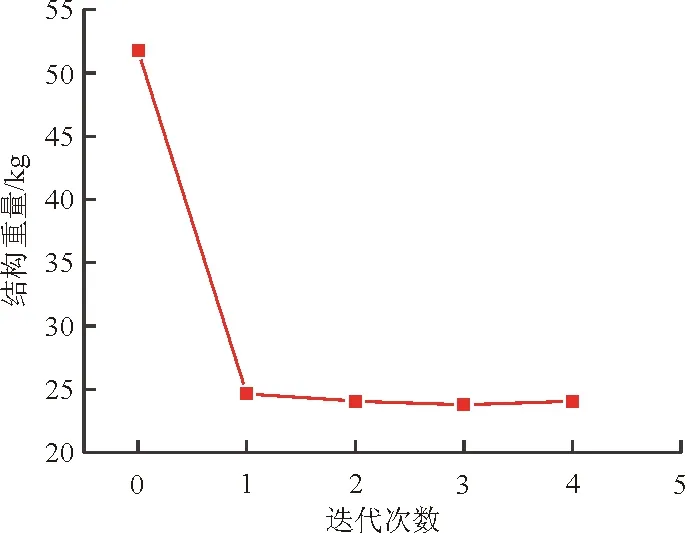
图4　优化区域2结构质量优化过程中的变化规律

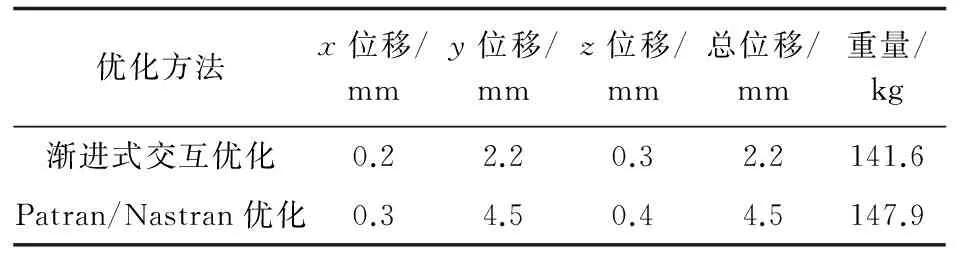
优化方法x位移/mmy位移/mmz位移/mm总位移/mm重量/kg渐进式交互优化0.22.20.32.2141.6Patran/Nastran优化0.34.50.44.5147.9

4结论

(1) 使用渐进式交互优化设计，在建立壁板的初始有限元模型时，无需对加强筋的形状和间距进行网格划分，可以快速地对粗糙有限元模型开展分析。

(2) 使用HyperSizer，其拓扑优化与尺寸优化是同时进行的，优化更加合理；如果单用Patran/Nastran进行优化，需要先进行一轮拓扑优化，确定壁板上加筋的位置、数目等，在此基础上再进行尺寸优化，以确定壁板、筋条的厚度等参数。

(3) 采用渐进式交互优化，与单用Patran/Nastran优化相比，可减重5%左右。

参考文献

[1] 彭云， 易龙， 南英. 复合材料盒段结构屈曲稳定性分析及优化技术[J]. 航空计算技术， 2006， 36(5): 80-82.

Peng Yun, Yi Long, Nan Ying. Analysis and optimal design of the buckling stability of a composite box[J]. Aeronautical Computing Technique， 2006， 36(5): 80-82.(in Chinese)

[2] 程家林， 冯玉龙， 姚卫星. 复合材料加筋板结构优化设计的并行子空间法[J]. 航空工程进展， 2013， 4(3): 292-298.

Cheng Jialin, Feng Yulong, Yao Weixing. Concurrent subspace optimum design method for composite stiffened panel[J]. Advances in Aeronautical Science and Engineering， 2013， 4(3): 292-298.(in Chinese)

[3] Berke L, Patnaik S N, Murthy P L N. Optimum design of aerospace structural components using neural networks[J]. Computers & Structures, 1993, 48(6): 1001-1010.

[4] Blair M， Hill S， Weisshaar T A. Rapid modeling with innovative structural concepts[R]. AIAA-98-1755, 1998.

[5] 张铁亮， 丁运亮. 复合材料加筋壁板的结构布局优化设计[J]. 南京航空航天大学学报， 2010， 42(1)： 8-12.

Zhang Tieliang， Ding Yunliang. Structural layout optimization of composite stiffened panel[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010， 42(1)： 8-12.(in Chinese)

[6] Rikards R, Abramovich H, Auzins J, et al. Surrogate models for optimum design of stiffened composite shells[J]. Composite Structures, 2004, 63(2): 243-251.

[7] Nagendra S， Jestin D， Gurdal Z， et al. Impvoved genetic algorithm for the design of stiffened composite panels[J]. Computers & Structures, 1996, 58(3)： 543-555.

[8] Fatemi J, Trompette P. Optimization of stiffened plates using a modified genetic algorithm[R]. AIAA-98-4973, 1998.

[9] Kang J H, Kim C G. Minimum-weight design of compressively loaded composite plates and stiffened panels for post buckling strength by genetic algorithm[J]. Composite Structures， 2005, 69(2): 239-246.

[10] Lanzi L, Bisagni C. Minimum weight optimization of composite stiffened panels using neural networks[R]. AIAA-2003-1698, 2003.

[11] 李烁， 徐元铭， 张俊. 基于神经网络响应面的复合材料结构设计[J]. 复合材料学报， 2005， 22(5)： 134-140.

Li Shuo， Xu Yuanming， Zhang Jun. Composite structural optimization design based on neural networks response surfaces[J]. Acta Materiae Compositae Sinica, 2005， 22(5)： 134-140.(in Chinese)

[12] Liu Wenli, Butler R, Mileham A R, et al. Optimum design, experimental testing and posy-buckling analysis of thick composite stiffened panel[R]. AIAA-2005-1826， 2005.

[13] 赵群， 丁运亮， 金海波. 一种基于复合材料加筋板结构效率的稳定性优化方法[J]. 复合材料学报， 2010， 27(3)： 169-176.

Zhao Qun, Ding Yunliang, Jin Haibo. Buckling optimization methdod based on structure efficiency of composite stiffened panels[J]. Acta Materiae Composite Sinica， 2010， 27(3)： 169-176.(in Chinese)

[14] 吴莉莉， 姚卫星. 复合材料加筋板结构的二级协同优化设计方法[J]. 南京航空航天大学学报， 2011， 43(5)： 645-649.

Wu Lili, Yao Weixing. Two-level collaborative optimum design method for composite stiffened panel[J]. Journal of Nanjing University of Aeronautics & Astronautics， 2011, 43(5): 645-649.(in Chinese)

[15] 卢秉贺， 李萍, 张军伟. 基于Patran/Nastran和HyperSizer的复合材料后机身加筋结构形式选择分析[J]. 民用飞机设计与研究， 2012(2): 53-55.

Lu Binghe, Li Ping, Zhang Junwei. Research stiffened structure configuration of laminated composite fuselage based on Patran/Nastran and HyperSizer[J]. Civil Aircraft Design & Research， 2012(2): 53-55.(in Chinese)

[16] 裘健全. 复合材料结构分析&优化——HyperSizer渐进式设计过程[J]. 材料工程, 2009(S2): 83-88.

Qiu Jianquan. Composite structural analysis & optimization-HyperSizer progressive design process[J]. Material Engineering, 2009(S2): 83-88.(in Chinese)

Composite Material Door Structural Progressive Optimization Design Based on HyperSizer

Li Yufeng, He Gao

(The First Aircraft Design and Research Institute, Aviation Industry Corporation of China, Xi’an 710089, China)

Abstract:Structure weight is the significant factor and constrained condition which should considered in composite aircraft structure design.Aimed at composite material door structure of an aircraft, the FEM(finite element model) is built and the analysis is carried out by using of Nastran/Patran. The progressive optimization is finished by Hypersizer. The optimum results are obtained according to the design requirements. The parameters of cross section, angle of each plies and stacking sequence are calculated. Methods of establishment of FEM and procedure of progressive optimization are summarized. Results show that after the optimization, the mass of structure decreases and the structure meets the required design target.

Key words:composite material; door; progressive optimization; HyperSizer

收稿日期：2015-11-25；修回日期：2016-05-04

通信作者：李宇峰,87433180@qq.com

文章编号:1674-8190(2016)02-230-05

中图分类号：V214.8

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.02.014

作者简介：

李宇峰(1982-)，男，工程师。主要研究方向：飞机结构设计。

贺高(1957-)，男，研究员。主要研究方向：翼面结构、复合材料结构设计。

(编辑：马文静)