基于Petri网的飞机复杂系统可靠性分析方法研究

郭鹏

(中国航空工业集团公司 第一飞机设计研究院，西安　710089)

基于Petri网的飞机复杂系统可靠性分析方法研究

郭鹏

(中国航空工业集团公司 第一飞机设计研究院，西安710089)

摘要：Petri网在建模方面具有较强的可视性及良好的动态表达性，提出一种利用Petri网对飞机复杂系统进行可靠性建模的方法，并通过蒙特卡洛仿真方法对Petri网模型进行仿真求解，形成一套完整的可靠性分析理论；以某型机电传飞控系统为例进行建模计算，验证上述方法的可行性和精确性。结果表明：本文提出的基于Petri网的可靠性分析理论，能够有效应用于飞机复杂系统的可靠性分析。

关键词：Petri网；复杂系统；蒙特卡洛仿真；可靠性分析；电传飞控系统

0引言

可靠性工作贯穿于产品的全寿命过程中，其主要技术内容包括可靠性预计、可靠性设计、可靠性试验、可靠性分析与评估等[1]。目前在可靠性分析中具有许多建模方法，例如可靠性框图模型、故障树分析(Fault Tree Analysis，简称FTA)模型、故障模式及影响分析方法(Failure Modes and Effect Analysis，简称FMEA)等。随着科学技术的快速发展，系统结构日趋复杂，其复杂性不仅是规模和结构的简单放大，还体现在系统的动态特性、工作条件以及功能层次等方面[2]。复杂系统的大量出现，对可靠性的要求也越来越高[3]。传统的可靠性框图法只是一种静态的建模和分析方法；故障树模型既未考虑故障发生的时序关系，也未涉及模糊事件的处理，FMEA方法无法准确地对系统的结构知识、功能知识、行为知识和目标知识进行全面地描述[4]。综上所述，传统的可靠性分析模型都因各种缺陷，无法准确描述复杂系统的可靠性。

1962年，C.A.Petri[5]首次提出了Petri网的概念。此后，其理论得到了不断地发展。Petri网的抽象描述能力不断地向纵向和横向发展，其纵向扩展表现为从基本的条件/时间网发展到谓词/变迁网和着色网，其横向扩展表现为从没有参数的网，发展到时间Petri网、随机Petri网等[6]。经过五十多年的发展，Petri网在许多领域得到了成功的应用，例如通信协议、系统性能评估、柔性制造等，并在航空领域得到了快速地发展，例如飞机维修性、测试性和可靠性等方面[7-9]。

Petri网模型具有强的可视性，且可动态演示系统运行过程，这是其他模型(例如故障树、FMEA等)所做不到的。例如，目前应用较多的是利用Petri网的逻辑描述能力代替故障树进行系统可靠性分析建模，可将故障树模型转换为相应的Petri网模型。根据得到的Petri网能够写出关联矩阵，通过关联矩阵，能够快速得到故障树的最小割集[10]。 T.S.Liu等[11]给出了各种复杂故障树关系的Petri网表示方法。

鉴于Petri网在可靠性分析中的技术优势，本文通过对Petri网基本理论及其高级理论的分析与研究，提出利用Petri网进行飞机复杂系统可靠性分析的方法；即通过赋予库所、托肯和变迁工程化定义，借助复杂系统的可靠性信息，构建出其对应的Petri网模型。对Petri网模型进行节点排序与蒙特卡罗仿真后，获得复杂系统的可靠性仿真结果；通过将上述方法在某型机的电传飞控系统中进行应用，验证基于Petri网的可靠性分析方法是否适用于飞机复杂系统的可靠性分析，以期该方法广泛应用到型号的可靠性设计中。

1Petri网理论

1.1Petri网基础理论

Petri网是一种网状信息流模型，包括条件和事件两类节点，在条件和事件为节点的有向二分图的基础上添加表示状态信息的托肯分布，并按照一定的引发规则使得事件驱动状态演变，从而反映系统的动态运行过程。通常情况下，用小矩形或者短黑线表示事件节点，称为变迁；用小圆圈表示条件节点，称为库所。两个变迁节点和库所节点之间不能使用有向弧相连，而变迁节点和库所节点之间可以使用有向弧连接，由此构成的有向二分图称为网。网的某些库所节点中标上若干个黑点表示托肯，从而构成Petri网。Petri网通过上述几类简单元素可完整有效地描述系统的动态运行过程(如图1所示)，可以看出：通过变迁点火促使库所中托肯流动，可完成系统动态过程的描述。

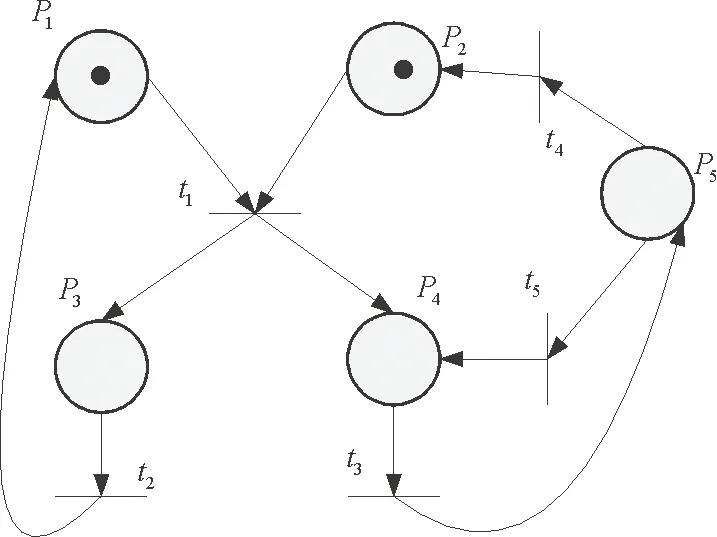
图1　简单Petri网示意图

1.2Petri网可靠性分析理论

简单Petri网并不能对工程系统的故障网络予以分析评估，在对基本Petri网恰当地注入随机信息函数驱动后，通常称为随机Petri网。随机Petri网最早由D.Shadiros提出的，此后许多结合随机过程理论和各具特色Petri网被提出，例如广义有色随机Petri网[12]等。1979年Kurt Jensen[13]提出了加入个性托肯的有色Petri网。有色Petri网利用网络图形描述对象之间的输入输出关系，很好地反映了系统的静态和动态特性，其动态特性通过托肯(托肯颜色可表示资源的共性和个性)的移动和传播进行控制。因此，有色Petri网在可靠性建模与仿真领域得到了广泛的发展。

基于上述Petri网理论，本文提出一种基于随机Petri网和有色petri网特点的Petri网进行复杂系统的可靠性分析。该Petri网一方面保留了随机Petri网的特点，即通过关联时间变迁参数，对复杂系统内故障模式的动态行为进行定量描述；另一方面通过对不同的故障模式进行颜色定义，以此追溯判断不同故障模式对复杂系统中最终影响程度。其构成元素为两类库所、六类托肯、两类变迁及两类有向流，该Petri网模型的简单示意如图2所示。

(1) 两类库所

①LRU正常工作状态的库所，每个LRU对应唯一的该类库所。

②LRU/子系统/系统故障状态的库所，每个LRU/子系统/系统对应唯一的该类库所。LRU/子系统/系统可能存在多种故障模式，每一种故障模式都对应着一个有色托肯，故该类库所可存在多个有色托肯。

(2) 六类托肯

根据天气预报颜色预警原理，对托肯按照故障模式的影响程度依照不同的颜色进行分类，分类情况如下(注：为了方便不同颜色的故障模式在Petri网图中的表示，可直接用相应的颜色英文单词首字母代替)：Ⅰ灾难级为红色(R)；Ⅱ严重级为橙色(O)；Ⅲ轻度级为黄色(Y)；Ⅳ轻微级为蓝色(B)；Ⅴ正常工作状态为绿色(G)；Ⅵ正常却不工作状态为白色(W)。

(3) 两类变迁

①延时变迁：表示LRU正常工作状态到LRU某故障模式的演化过程(内因)。该类变迁一般服从某个概率分布函数。如果LRU存在n个故障模式(不包括正常但不工作模式)，那么该LRU就有n个这样的延时变迁。

②瞬时变迁：表示故障传播途径的诱因(外因变迁)。

(4) 两类有向流

①LRU正常工作模式→延时变迁→LRU故障模式(内因故障传播)。

②LRU/子系统/系统故障模式→瞬时变迁→LRU/子系统/系统故障模式(外因故障传播)。

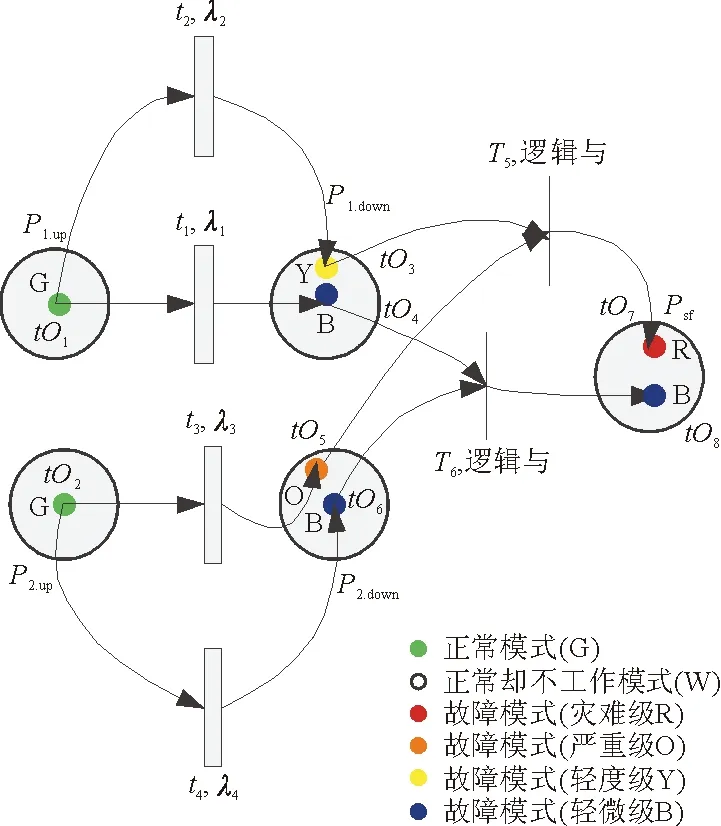
图2　可靠性分析的Petri网

2系统可靠性分析流程

飞机复杂系统可靠性分析的完整流程如图3所示。

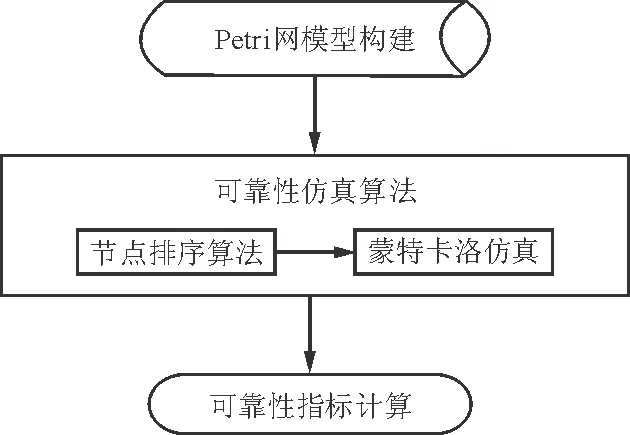
图3　可靠性分析流程图

具体包括以下三个步骤：

(1) Petri网模型构建。需对飞机复杂系统的可靠性功能逻辑关系进行分析，建立系统随机有色Petri网模型，主要步骤如下：

①以LRU级元件为库所单元，对库所单元注入多类型故障模式的托肯，即利用天气预报颜色预警原理对不同托肯赋予不同的颜色。完成各LRU元件正常状态向故障模式转化的时间过程表示。具体过程：为各LRU建立表示其正常工作状态的库所，并为库所放置绿色托肯；建立延时变迁，并为其关联故障模式服从的概率分布(例如指数分布)；通过延时变迁连接正常模式的绿色托肯与表示LRU故障模式的有色托肯。

②对复杂工程系统中的所有子系统/系统建立库所，并依据子系统/系统故障严重级别放置相应颜色托肯。

③对各库所内的有色托肯建立瞬时变迁，按照工程物理系统的功能逻辑关联实施有向弧构造，以完成不同LRU之间、LRU与子系统、子系统与子系统、子系统与系统等之间故障传播过程的表示。

(2) 可靠性仿真算法。即利用节点排序算法对建立的Petri网模型获取Petri网链接顺序表，再利用蒙特卡洛仿真进行N次仿真。

(3) 可靠性指标计算。即以蒙特卡洛仿真为基础，通过对Petri网模型中的库所、变迁状态(变迁是否发生)进行统计，获得系统可靠度等指标。

3案例应用

3.1系统描述

以某型机电传飞控系统为例进行可靠性分析。该电传飞控系统采用“具有自监控功能的数字四余度计算机(PFC)+作动器控制器(ACE)”的体系结构。进行可靠性分析，只需关注对系统可靠性影响较大的子系统和LRU，因此对电传飞控系统进行适当简化，去除对电传飞控系统可靠性影响较小的LRU，其简化后的功能关系如图4所示。

图4　电传飞控系统功能关系

3.2建模过程

在电传飞控系统建模之前，需要对系统/子系统/LRU进行三级编号。根据ATA编号规则要求，电传飞控编号为27；子系统的编号分别为27-01，27-02，……，27-06；LRU的编号类似，即分别为27-01-XX，27-02-XX，27-03-XX，27-04-XX，27-05-XX，27-06-XX。

电传飞控系统的具体建模过程如下：

①此处以水平安定面作动器1为例(编号为27-05-25)，存在一种故障模式，表示为RD.1，则应为其库所内放置一个红色托肯，编号为RD.1，水平安定面作动器1的编号即为库所编号(27-05-25)。同理，可为系统内的所有LRU建立相应的库所和表示故障模式的有色托肯。

②仍以水平安定面作动器1为例，为该LRU建立一个放置绿色托肯的库所，并建立关联故障模式服从指数分布的延时变迁(如图5所示)。同理，可完成整个系统内所有LRU元件正常模式向故障模式转化的时间过程表示。

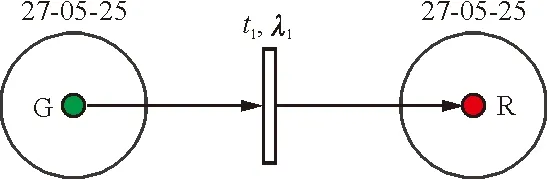
图5　水平安定面作动器1Petri网图

③对电传飞控系统及各子系统建立库所和托肯，如图6～图7所示。

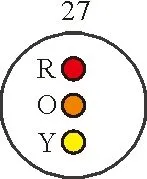
图6　电传飞控系统的库所、托肯图

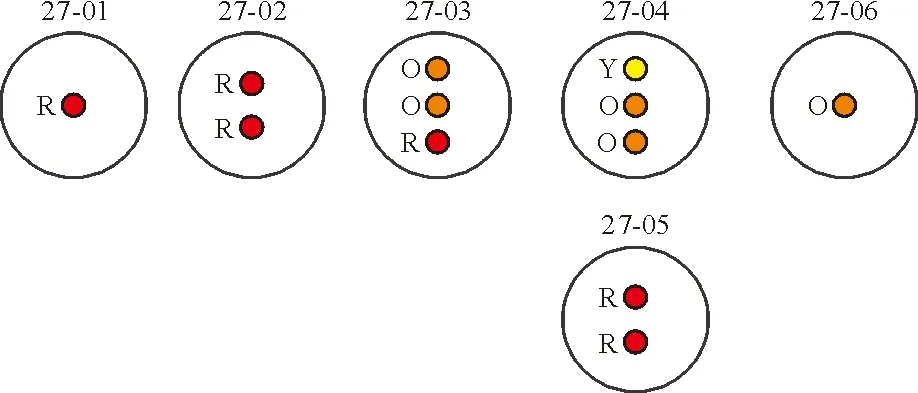
图7　电传飞控系统各子系统的库所、托肯图

④仍以水平安定面作动器1为例，建立LRU与系统之间的故障传播关系(如图8所示)，同理可建立系统内其他LRU到子系统之间的故障传播关系。子系统之间的故障传播关系以及子系统到系统的故障传播关系如图9～图10所示，连接LRU与子系统之间、子系统与子系统之间、子系统到系统间的故障传播关系，即可得到电传飞控系统完整的Petri网图。

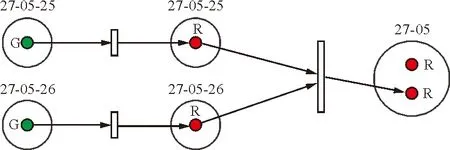
图8　水平安定面作动器与子系统间故障传播

图9　电传飞控子系统之间的故障传播过程

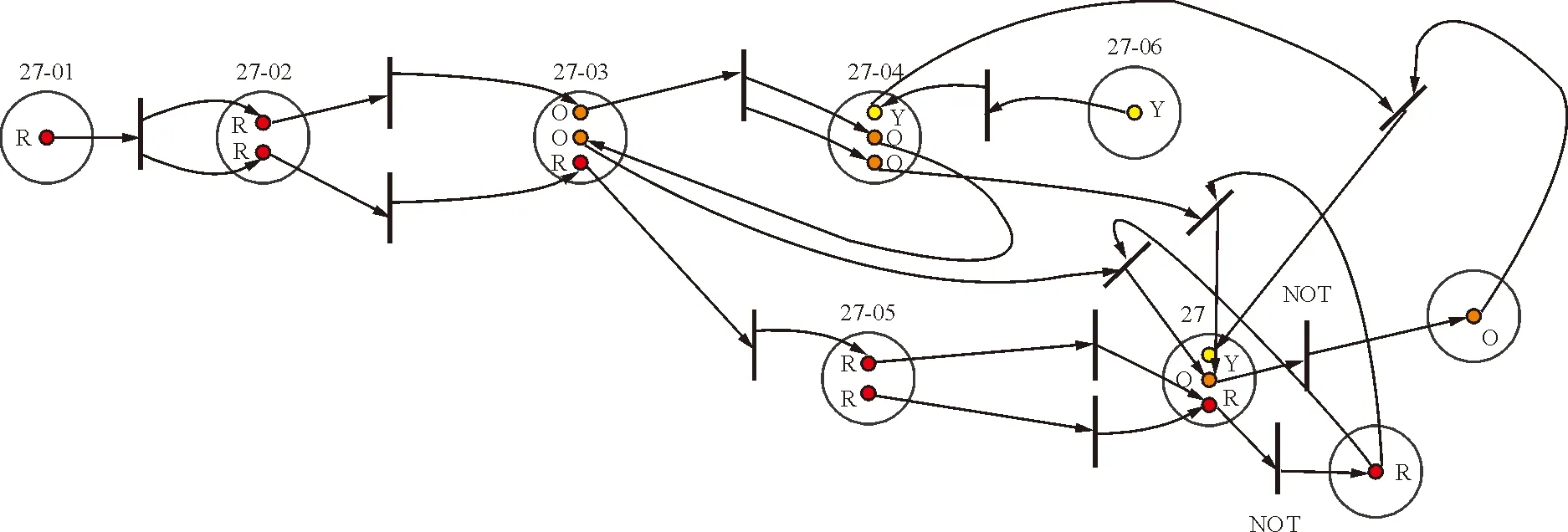
图10　电传飞控子系统到系统故障传播过程

3.3仿真结果

以100 FH为一步长，对100 000 FH内的电传飞控系统进行20 000次可靠性仿真(当仿真次数超过20 000时，数据结果趋于稳定；当仿真次数低于20 000时，偏差较大)，获得1 000组仿真数据，对其进行拟合，结果如图11～图12所示。

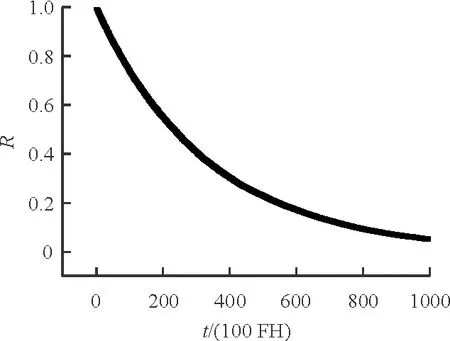
图11　电传飞控系统可靠度

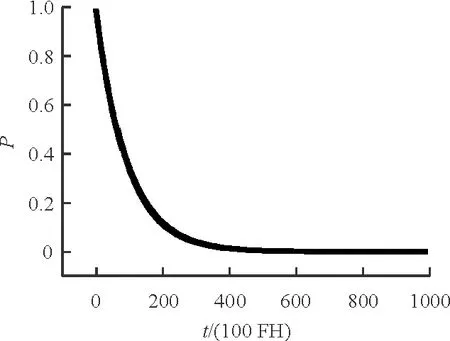
图12　电传飞控系统正常模式工作概率

电传飞控系统工作模式包括正常工作模式、降级工作模式和模拟备份工作模式。当模拟备份失效时，电传飞控系统完全失效，进入机械备份状态。

从图11～图12可以看出：电传飞控系统的可靠度比正常工作模式概率高，得益于系统降级工作模式和模拟备份模式的补充，与实际情况相符。

从图12可以看出：正常工作模式下，电传飞控系统飞行时间超过20 000 FH后，其可靠度趋近于0。为了验证上述结果的正确性，通过Isograph软件对电传飞控系统进行任务可靠性(正常工作模式)预计，结果如表1所示。

表1　电传飞控系统任务可靠性预计与仿真对比

从表1可以看出：在1 000 FH内，电传飞控系统的任务可靠性仿真值与预计值误差较小，并且飞行时间越短，其误差越小；电传飞控系统工作1 000 FH后，其可靠性仿真值与预计值得误差仅为2.460%。

为了进一步验证仿真结果的精确性，分别对飞控系统飞行5 000，10 000，20 000，40 000，60 000,80 000,100 000 FH的任务可靠性进行预计，并绘制相应的曲线，如图13所示。

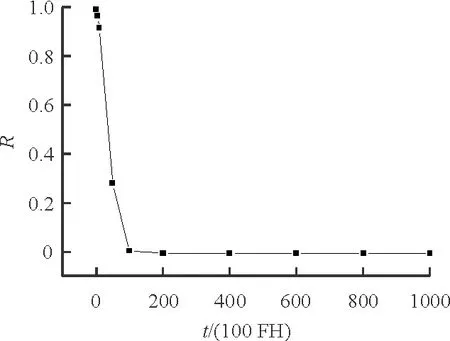
图13　电传飞控系统任务可靠性曲线

从图12～图13可以看出：电传飞控系统正常工作模式曲线与任务可靠性预计曲线在1 000 FH内的误差很小，在10 000～20 000 FH内的区间误差较大，但二者总体趋势一致并最终收敛。通常电传飞控系统任务剖面内的飞行时间不会超过6 h，相对误差极小，因此可认为任务剖面时间不影响最终的仿真结果。

4结论

(1) 基于Petri网理论，提出了针对飞机复杂系统进行可靠性分析的完整方法。同时，对某型机的电传飞控系统进行可靠性建模与仿真计算。为了验证仿真结果的精确性与适用性，对电传飞控系统进行任务可靠性预计。

(2) 在1 000 FH以内，基于Petri网的可靠性分析方法能够对复杂系统的可靠度进行精确仿真。

(3) 鉴于飞机系统任务时间较短，基于Petri网的可靠性分析方法适用于飞机复杂系统的可靠性计算，可广泛应用到飞机型号的设计中。

参考文献

[1] 曾天翔， 杨先振， 王维翰. 可靠性及维修性工程手册[M]. 北京： 国防工业出版社， 1994.

Zeng Tianxiang, Yang Xianzhen, Wang Weihan. Reliability & maintainability engineering manual[M]. Beijing： National Defense Industry Press, 1994.(in Chinese)

[2] 覃庆努. 复杂系统可靠性建模分析和综合评价方法研究[D]. 北京： 北京交通大学， 2012.

Qin Qingnu. The reliability modeling, analysis and comprehensive evaluation method of complex systems[D]. Beijing： Beijing Jiaotong University, 2012.(in Chinese)

[3] 郭波， 武小悦. 系统可靠性分析[M]. 长沙： 国防科技大学出版社, 1992.

Guo Bo, Wu Xiaoyue. System reliability analysis[M]. Changsha： National University of Defense Technology publishing, 1992.(in Chinese)

[4] 胡涛， 俞建， 董鹏. 基于功能建模的复杂系统FMEA方法研究[C]. 海口： 中国电子学会可靠性分会， 2008.

Hu Tao, Yu Jian, Dong Peng. Research on complex system FMEA method based on functional modeling[C]. Haikou： Reliability Branch, Chinese Institute of Electronics, 2008.(in Chinese)

[5] 乐晓波， 陈黎静. Petri网应用综述[J]. 长沙交通学院学报， 2004, 20(2)： 51-55.

Yue Xiaobo, Chen Lijing. Research surveys on application of the Petri net[J]. Journal of Changsha Communications University, 2004, 20(2)： 51-55.(in Chinese)

[6] 张斌. 基于变迁可靠性与可维修性的Petri网主干路径寻优[D]. 西安： 西安建筑科技大学， 2008.

Zhang Bin. Optimum route sequence search in Petri net based on reliability and reparability of transition[D]. Xi’an: Xi’an University Architecture and Technology, 2008.(in Chinese)

[7] 汤新民， 钟诗胜. 基于Petri网航空维修分解装配序列规划及其应用[J]. 中国民航学院学报， 2006， 24(5)： 21-22.

Tang Xinmin, Zhong Shisheng. Petri nets based on aircraft maintenance disassembly and assembly process planning[J]. Journal of Civil Aviation Flight University of China, 2006， 24(5)： 21-22.(in Chinese)

[8] 王修岩， 薛斌斌, 李宗帅. 基于Petri网的飞机交流发电机故障诊断方法研究[J]. 计算机测量与控制， 2012, 20(4)： 878-879.

Wang Xiuyan, Xue Binbin, Li Zongshuai. Fault diagnosis methods of aircraft AC generator based on Petri nets[J]. Computer Measurement & Control， 2012, 20(4)： 878-879.(in Chinese)

[9] 曹健， 魏晨. 基于Petri网的飞控计算机系统可靠性建模与分析[J]. 系统仿真学报， 2010， 22(1): 239-242.

Cao Jian, Wei Chen. Reliability modeling and analysis of flight control computer system based on Petri net[J]. Journal of System Simulation， 2010， 22(1): 239-242.(in Chinese)

[10] 于开民， 孙时珍， 张树团， 等. 一种基于Petri网的飞机配电系统可靠性分析方法[J]. 电子设计工程， 2010， 18(10): 133-135.

Yu Kaimin, Sun Shizhen, Zhang Shutuan, et al. A mehod for reliability assessment of airplane power distribution system based on Petri network[J]. Electronic Design Engineering， 2010， 18(10): 133-135.(in Chinese)

[11] Liu T S, Chiou S B. The application of Petri nets to failure analysis[J]. Reliability Engineering and System safety, 1997, 57: 129-142.(in Chinese)

[12] 范玉顺, 吴澄, 杨建华. FMS可靠性指标计算的有色广义随机Petri网方法[J]. 计算机技术与自动化， 1997, 16(4)： 1-5,8.

Fan Yushun, Wu Cheng, Yang Jianhua. The calculation of FMS reliability of generalized stochastic Petri nets methodology[J]. Computing Technology and Automation, 1997, 16(4)： 1-5,8.(in Chinese)

[13] Kurt Jensen. Colored Petri net and the invariant-method[J]. Theoretical Computer Science, 1981(14): 317-336.

Research on the Reliability Analysis Method of the Complex Aircraft System Based on the Petri Net

Guo Peng

(The First Aircraft Design and Research Institute, Aviation Industry Corporation of China， Xi’an 710089, China)

Abstract:As the Petri net has good visibility and excellent dynamic expressiveness, a method of utilizing Petri net to carry on reliability modeling on complex system is introduced. Through simulating the formed Petri net model of the complex system by means of the Monte Carlo simulation, which has formed a whole theory on reliability analysis, the computation results can be obtained. Finally, the case of fly-by-wire flight control system is applied, to prove the validity and accuracy of the above methodology. Results show that the reliability analysis method based on Petri nets can be applied to the complex aircraft system efficiently.

Key words:Petri net; complex system; Monte Carlo simulation; reliability analysis; fly-by-wire flight control system

收稿日期：2016-02-02；修回日期：2016-04-15

通信作者：郭鹏,510164458@qq.com

文章编号:1674-8190(2016)02-174-07

中图分类号：TP391.9; V215.7

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.02.006

作者简介：

郭鹏(1987-)，男，硕士，工程师。主要研究方向：飞机可靠性设计。

(编辑：赵毓梅)