增广拉格朗日子集模拟优化方法

董乔月，李洪双

(南京航空航天大学 航空宇航学院，南京　210016)

增广拉格朗日子集模拟优化方法

董乔月，李洪双

(南京航空航天大学 航空宇航学院，南京210016)

摘要：传统的工程结构优化设计方法在求解多设计变量、多约束条件的结构优化设计问题时，存在诸多不足，针对上述问题，基于增广拉格朗日约束处理方法和子集模拟优化方法发展一种新的结构优化设计方法——增广拉格朗日子集模拟优化方法(ALSSO)。该方法首先利用拉格朗日乘子法处理多重约束条件，然后利用子集模拟优化方法对转化后的无约束优化问题进行求解；对罚函数因子的更新方法进行改进，以保证收敛过程的稳定性；利用两个算例对该方法的计算精度、稳健性以及计算效率进行验证，并与其他优化方法进行对比。结果表明：增广拉格朗日子集模拟优化方法具有非常优秀的寻优性能。

关键词：结构优化设计；子集模拟优化方法；拉格朗日乘子法；罚函数因子

0引言

结构优化设计问题在工程结构设计中较为常见，20世纪40年代以前，多采用图解法、数学求极值和经典力学分析法研究简单结构的最小质量设计问题；20世纪50年代后，随着数学建模和计算机技术的完善，对工程系统进行自动优化设计技术得到迅速发展和应用。计算机能在给定条件下得到最优设计方案，缩短设计周期，提高设计质量[1]。

工程结构优化问题通常是在多重约束条件下使所设计结构的重量最轻或者费用最低，约束条件是指对结构的应力、位移、屈曲等力学响应量的限制。而在实际应用中，求解有约束优化问题是非常困难的，其原因是：①设计变量的数量多，②可行域的高度不规律，③约束条件的数量多。因此，人们不断寻求、探索既能在复杂设计区域中进行最优解的搜索，又可处理多重约束条件的优化方法。

目前，工程上所用的优化方法大致可分为两类：一类是基于梯度的数值优化方法，另一类是基于自然现象的启发而发展的随机型优化方法。随着工程结构优化问题越来越复杂，采用基于梯度的数值优化方法进行求解后的优化结果的可信度也在逐渐减小，其原因是当求解优化问题遇到上文所提的三个问题时，数值优化方法得出的优化结果通常不是全局最优的，甚至可能是不可行的。而随机型优化方法在处理上文所提的三个问题时，能够弥补数值优化方法的缺点和不足，因此受到了高度关注。虽然目前已有较多的随机型优化方法且在结构优化设计领域被广泛应用，例如遗传算法[2]、粒子群优化算法[3]、模拟退火算法[4]、蚁群优化算法[5]、和声搜索算法[6]等，但仍没有一种优化方法可以求解所有的结构优化设计问题，寻找更加高效、稳健的随机型优化方法是未来努力的方向。

本文基于子集模拟优化方法，结合拉格朗日乘子法，发展一种用于求解有约束优化问题的增广拉格朗日子集模拟优化方法，采用两个典型算例验证所发展方法的寻优能力、稳健性以及计算效率，并与其他优化设计方法进行对比。

1子集模拟优化方法原理

子集模拟(Subset Simulation)是一种高效的蒙特卡罗策略，最初被用于求解高维小失效概率结构可靠性问题[7]，后期研究表明，子集模拟也是一种随机型优化方法[8-9]。其基本思想是：一个极值事件(优化问题)可以看作是一个稀有事件(可靠性问题)的特例，二者之间的转换关系如图1所示。

图1　优化问题与可靠性问题之间的转换

考虑如下无约束全局优化问题：

maxh(x)x∈S

(1)

式中：h(x)为目标函数；x∈S为设计变量集合；S为问题定义域。

为了在可靠性问题的框架内研究优化问题，人为地令设计变量x为随机变量并且指定(用户定义)概率分布类型，因此所得到的目标函数也是随机变量，并且具有其自身的概率密度函数与累积分布函数。上述将确定性的变量“拓展”为随机变量的概念是利用蒙特卡罗策略解决复杂问题的一种计算方法。设定hopt是h的全局最大值，此时有x=xopt。累积分布函数的性质决定了累计分布函数曲线必定是右连续且单调不减的。可靠性问题中所寻找的“失效概率”PF定义为

PF=P(F)=P[h(x)≥hopt]

(2)

式中：失效事件F=[h(x)≥hopt]。

显然，失效概率等于0，因为hopt为全局最大值。在优化问题中，并不关注该失效概率，而是重点研究目标函数达到最大值的点或区域。

子集模拟方法的思想为：在式(2)中，P[h(x)≥hopt]可以表示为一系列条件概率的乘积。条件概率{pi:i=1,2,…}用于定义中间失效事件，中间失效事件相应的分界值{hi:i=1,2,…}由式(3)估计给出。

(3)

式中：Fi为由模拟过程中的目标函数值所确定的中间事件。

根据乘法定理有：

(4)

在子集模拟优化中，改进的Metropolis-Hasting(MMH)算法[7]用于生成条件样本，并逐渐靠近目标函数的最大值。这相当于把可靠性问题中的稀有事件区域逐渐发掘出来。对于拥有至少一个全局最大值的优化问题，可以将寻找hi→hopt的过程看作是寻找PF→0的过程。在优化过程中，子集模拟算法生成一系列中间目标函数的值{hi:i=1,2,…}，它们最终趋向全局优化点hopt。同时，样本分布逐渐从概率密度函数(用户指定)定义的宽广区域，变为包含全局优化方案xopt在内的狭小区域。

子集模拟优化方法的运行过程如下：

(1) 选择输入变量的分布参数。在确定性优化算法中，每一个输入设计变量都是确定性参数，但是在子集模拟优化算法中，输入设计变量是随机的，并且有一个假设的概率密度函数(PDF)fi(xj)。

(3)MMH算法用于生成中间事件中的条件样本。在第k层迭代中，从Fk-1中每个“种子”样本开始生成一条马尔可夫链。由于初始样本服从条件分布，所有马尔可夫链都是平稳的，并且每条马尔可夫链上的样本都满足条件分布。每条马尔可夫链的长度为1/pk-1(k=2,…)，其中pk-1为上一层迭代的条件概率。为新生成的样本目标函数值进行计算与排序，从序列里确定第N(1-pk)个样本和相应的目标函数值，这些筛选出的样本为下一层迭代提供了“种子”样本。

(4) 重复上述步骤直到满足收敛条件或者达到最大可负担计算量。

(5) 关于无约束子集模拟优化方法的描述和讨论，详见参考文献[8]。

2增广拉格朗日子集模拟优化方法

2.1增广拉格朗日约束处理方法

拉格朗日乘子法将约束条件加入目标函数中，形成拉格朗日函数：

(5)

式中：λj为第j个约束的拉格朗日乘子；gj(x)为约束条件。

类似于罚函数方法，式(5)将有约束优化问题转变为无约束优化问题。拉格朗日函数可以作为无约束目标函数使用，原因是有约束优化问题的最优解同样适用于该无约束优化问题。但因为该解不一定是拉格朗日函数的最优解，所以为了保证该解的可行性与最优性，在增广拉格朗日函数中加入一个增广函数θ[10]，则整个函数为

(6)

(7)

式中：h(x)为第i个样本的目标函数值；ei(x)为等式约束违反值；gj(x)为不等式约束违反值；-λj/2rp,j从基于梯度的优化问题中选择得到[11]。

增广拉格朗日乘子法不同于标准的拉格朗日乘子法，因为多了罚函数一项；其也不同于标准的罚函数法，因为多项式里包括了拉格朗日乘子。在增广拉格朗日函数里，每个约束的可行性将使用一个单独的罚函数因子rp来判定。因为每个约束条件的罚函数因子是一个有限值，所以得出的结果必定是一个局部最优解[10]。最优点处的拉格朗日乘子和罚函数因子是未知的，且根据问题的不同而不同。每一层迭代过程中，拉格朗日乘子和罚函数因子都保持固定。每一层迭代之后，拉格朗日乘子根据该层优化结果进行如下更新[10]：

(8)

在迭代过程中，通过增大罚函数因子来阻止结果向不可行性方向发展，当约束值低于约束违反限定值εg时，罚函数因子便会减小[10]：

(9)

式中：ψj(xk)为等式或者不等式约束的约束违反值。

ψj(xk)的定义为

(10)

式中：ei(x)为等式约束的约束违反值；gj(x)为不等式约束的约束违反值。

罚函数因子的下限值为

(11)

2.2增广拉格朗日子集模拟方法的基本框架

增广拉格朗日子集模拟优化方法由两部分组成：外部循环用来构成增广拉格朗日函数，更新拉格朗日乘子和罚函数因子，并且检验优化过程是否收敛；在内部循环中，子集模拟优化算法求解无约束全局最优问题，即拉格朗日乘子和罚函数因子在内部循环中均保持固定值。增广拉格朗日子集模拟优化方法的流程图如图2所示。

图2　增广拉格朗日子集模拟优化方法流程图

内部循环中所使用的子集模拟优化方法在解决高维设计变量优化问题上具有优势，而本文发展的增广拉格朗日约束处理方法能够很好地处理多约束条件。增广拉格朗日子集模拟优化方法在处理多设计变量、多约束、复杂可行域的优化问题上表现出非常优秀的性能，将在第3节中通过多设计变量、多约束算例对此进行验证。

2.3初始化与迭代

最优解x*不能仅通过求解一个无约束优化问题而得到，这是因为拉格朗日乘子和罚函数因子的值是未知的，并且根据问题的不同而不同。因此，需要对拉格朗日乘子和罚函数因子设定初始值，在后续的迭代过程中，还应对二者进行更新，根据文献[10，12-13]，将拉格朗日乘子的初始值设定为0。

罚函数因子的初始值假设为一个单位矩阵，即r0=[1,…,1]T。K.Sedlaczek等[10]提出了一个更新罚函数因子的方法，即式(9)，但是该方法经常会造成罚函数因子的值在每层迭代时都产生数值上的变化，从而导致拉格朗日乘子在收敛过程中不稳定并且增加了计算量。

本文采用如下更新公式：

(12)

式中：φi(x*k)为计算约束违反值函数，对于等式约束，φi(x*k)=ei(x*k)，对于不等式约束，φi(x*k)=|gi(x*k)|。

与原始更新方法不同，改进后的更新方法只有在前一层迭代没有使得优化结果变好的情况下才会增加罚函数因子的值，当最优解x*k是一个可行解时，罚函数因子将保持一个确定值。

为了保证拉格朗日乘子更新的有效性，为所有罚函数因子值设定一个下限值：

(13)

在最初的迭代过程中，由于罚函数因子太小而不能得到有效的最优解，该下限值具有重要作用。

2.4收敛准则

收敛准则是对于外部循环而言的，经过增广拉格朗日方法处理过的优化问题的最初收敛准则为：如果λk-1和λk差的绝对值小于或等于给定的容限值ε，则可以判定优化过程已经收敛。但由于收敛过程中的不稳定性，改进后的优化方法使用另外一个收敛准则来保证优化结果的可行性。假设x*k是第k层迭代后得到的全局最优解，程序终止时，最优解满足：

ρ(x*k)≤ε

(14)

式中：ρ(x*k)为可行性标准。

ρ(x*k)的定义为

(15)

拉格朗日子集模拟优化方法在大多数情况下能够给出很好的优化结果，但在某些情况下，如果程序运行到最大迭代次数后仍未满足收敛准则，则最后一次迭代的最优解也可被看作是该优化问题的近似解。

3算例验证

将增广拉格朗日子集模拟优化方法用于求解桁架结构优化设计和机翼翼盒结构优化问题，并与其他著名优化算法进行对比。

桁架结构优化问题计算单层所用样本数为100、200和500，机翼翼盒结构优化问题单层所用样本数为100。所用条件概率p均为0.1。内部循环的子集模拟优化最大迭代次数选择为20，外部循环的最大迭代次数选择为50。子集模拟优化以及所有的约束容限都设定为ε=10-4。在桁架结构优化算例中，算例被运行30次来验证所发展优化算法的统计学性能，包括最好优化解、最差优化解以及平均优化解，并验证所发展算法的稳健性。

3.172杆空间桁架结构优化

72杆空间桁架结构如图3所示，桁架杆件材料的弹性模量为10 000ksi，材料密度为0.1lb/in3。

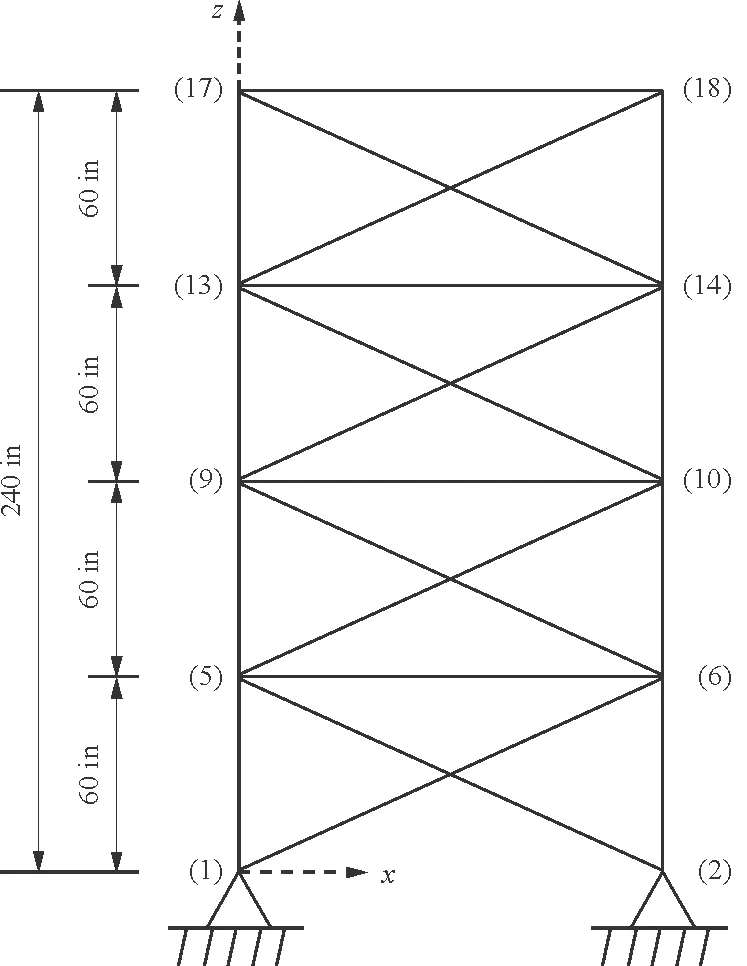
(a) 侧视图

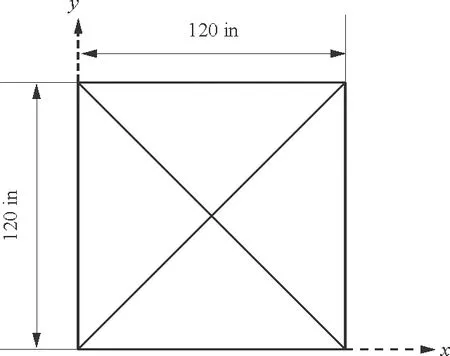
(b) 俯视图

(c) 斜视图

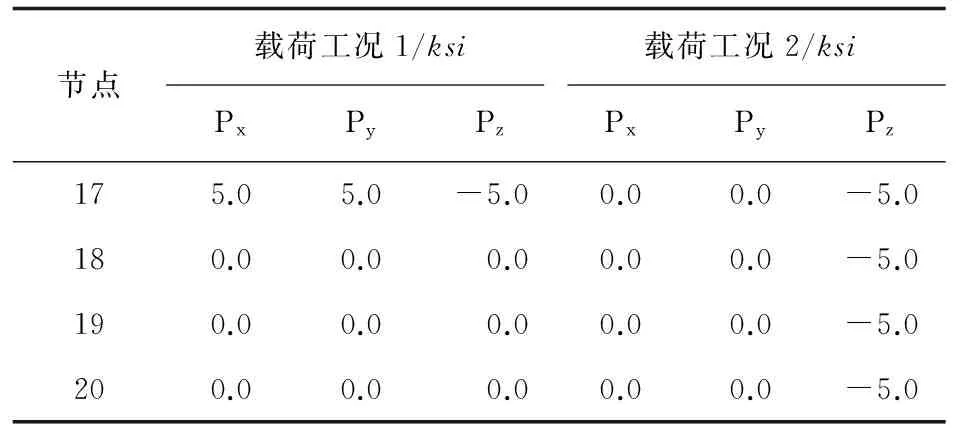
节点载荷工况1/ksi载荷工况2/ksiPxPyPzPxPyPz175.05.0-5.00.00.0-5.0180.00.0 0.00.00.0-5.0190.00.0 0.00.00.0-5.0200.00.0 0.00.00.0-5.0

72杆空间桁架结构优化问题已被遗传算法(GA)、蚁群优化算法(ACO)[14]、和声搜索算法(HS)[6]、粒子群优化算法(PSO)[15]及增广拉格朗日粒子群优化算法(ALPSO)[12]等多种优化算法求解过。增广拉格朗日子集模拟优化方法(ALSSO)的优化结果与上述优化算法优化结果的对比如表 2所示，表中同时给出了最优设计变量值、最小重量的优化结果、最大应力和最大位移的值。

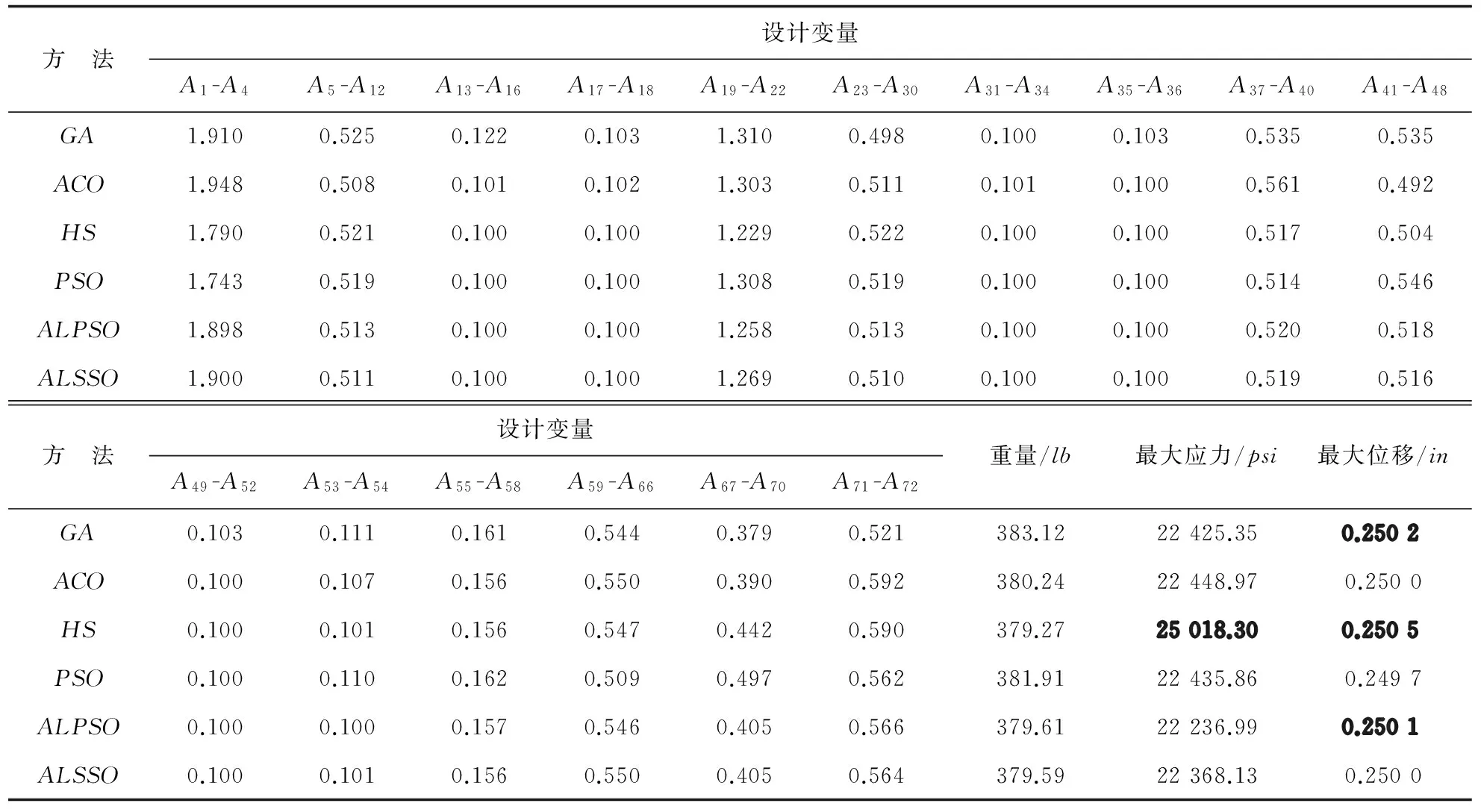
表2　72杆空间桁架结构优化结果对比

从表2可以看出：遗传算法、和声搜索算法、增广拉格朗日粒子群优化算法的优化结果均违反了位移约束条件，同时，和声搜索算法还违反了最大应力约束条件，故采用上述三种优化算法求解所得的最优解均为不可行解；在所有具有可行解的优化结果中，增广拉格朗日子集模拟优化方法的最终优化结果(379.59lb)优于蚁群优化算法的最终优化结果(380.24lb)和粒子群优化算法的最终优化结果(381.91lb)，表明增广拉格朗日子集模拟优化方法具有很好的寻优准确性。

随着优化迭代次数的增加，结构重量的优化过程如图4所示，优化过程所用单层样本数为500。

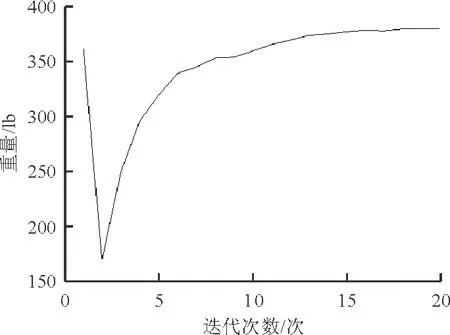
图4　72杆空间桁架结构迭代过程

从图4可以看出：在72杆空间桁架结构优化问题中，增广拉格朗日子集模拟优化方法在第17次迭代时便已收敛，得出的最优重量值为379.59lb，表明增广拉格朗日子集模拟优化方法的计算效率高、收敛快。

在72杆空间桁架结构优化问题中，增广拉格朗日子集模拟优化方法的统计学性能如表3所示，表中变异系数(COV)一列用来反映优化方法的稳健性。所有结果都是在30次独立运算后取得，所用单层样本数量分别为100、200和500。

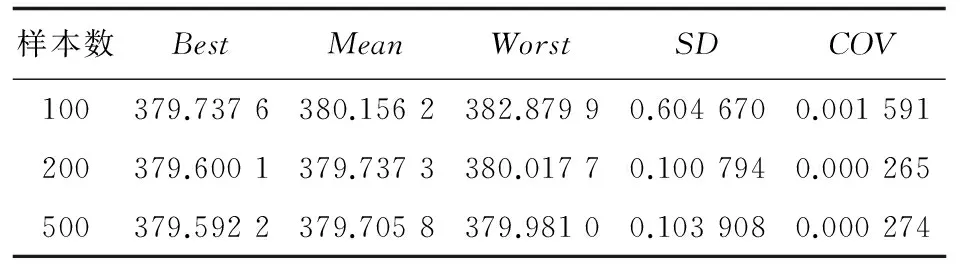
表3　72杆空间桁架结构统计学性能

从表3可以看出：三种样本量的变异系数值均很小，表明增广拉格朗日子集模拟优化方法具有很好的稳健性。

3.2机翼翼盒结构优化设计

机翼翼盒结构如图5所示，该结构关于x -y平面(结构中心面)对称。

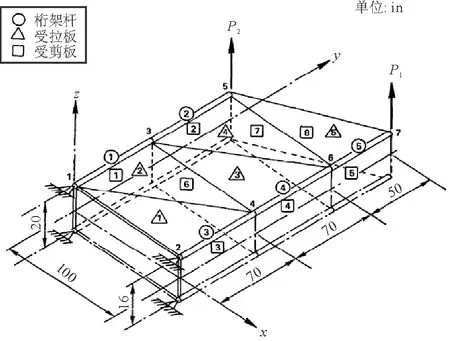
图5　机翼翼盒结构

选取机翼翼盒结构的上半部分作结构说明，在该结构的优化问题中，对于杆件单元，取杆件的横截面积为设计变量，横截面积的下限为0.1in2、上限为2.0in2。对于平面板，取板的厚度为设计变量，平面板分为受拉板(CST)和受剪板(SSP)，受拉板单元由矩形区域1243、矩形区域3465以及三角形单元567构成，其中两个矩形区域可分别看作由两个三角形受拉板构成，三个区域的受拉板厚度分别独立，受拉板厚度的下限为0.02in、上限为1.00in；受剪板厚度的下限为0.02in、上限为1.00in。机翼翼盒结构的节点坐标、桁架杆单元的编号与设计变量分组、受拉板单元的编号与设计变量分组以及受剪板单元的编号与设计变量分组参见参考文献[16]。整个机翼翼盒结构共16个设计变量，分别为5个杆件的横截面积，3个受拉板的厚度以及8个受剪板的厚度。在节点1和节点2处三个方向的位移边界条件为0。桁架杆、受拉板和受剪板所用材料相同，材料许用应力为10 000lb/in2，弹性模量为107lb/in2，密度为0.02lb/in3，泊松比为0.3。结构有两种载荷工况，分别为：在节点7处受沿z轴正向，大小为5 000lb的集中力；在节点5处受沿z轴正向，大小为10 000lb的集中力。机翼翼盒结构所受位移约束为各节点在z方向上的位移均不得超过2in，所受应力约束为各单元的许用应力是10 000lb/in2。

在Abaqus中通过参数化建模建立机翼翼盒结构的有限元模型。受拉板和受剪板采用S4R壳单元建立，桁架采用T3D2杆单元建立。整个模型结构通过共节点装配得到，边界条件设定为左边界四节点铰支。载荷工况设定为：在分析步1中设定模型结构受工况1中载荷作用，并在分析步2中取消工况1中的载荷作用；在分析步2中设定模型结构受工况2中的载荷作用。为了保证结构在两种工况下均达到最优设计，分别取分析步1与分析步2中的应力与位移分析结果，并设定两个分析步所得结果的最大值作为该优化问题的应力与位移约束结果。

利用增广拉格朗日子集模拟优化方法对该机翼翼盒结构进行优化设计，并与其他优化方法相比较，优化结果如表4所示，表中包括最优设计变量值和最小重量。ACCESS1优化方法[16]为NASA报告中提出的一种基于梯度的优化算法，Gallatly&Berke方法和Gallatly方法为R.A.Gallatly等[17-18]提出的优化算法。上述三种优化方法均为基于梯度的优化方法，并且所得出的最优解均满足结构所要求的位移及应力约束条件。

表4　机翼翼盒结构优化结果

从表4可以看出：增广拉格朗日子集模拟优化方法得出的最优设计明显优于其他方法所得的最优设计，表明增广拉格朗日子集模拟优化方法具有优秀的寻优能力。

机翼翼盒结构优化设计迭代过程如图6所示，所用单层样本数为100。

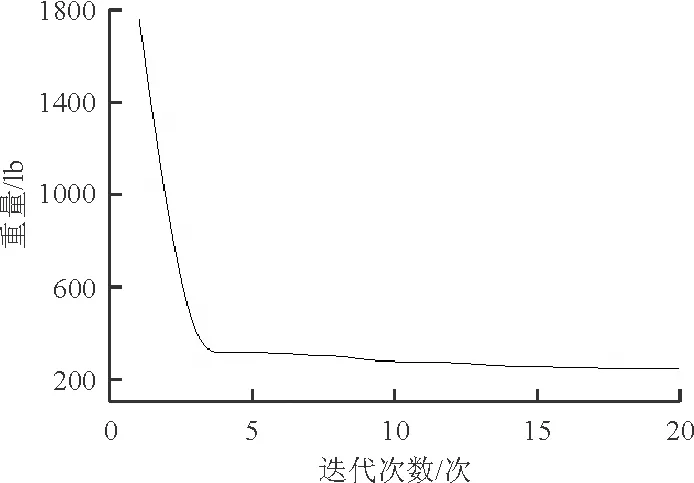
图6　机翼翼盒结构优化迭代过程

从图 6可以看出：在第15次循时该翼盒结构优化过程达到收敛，表明增广拉格朗日子集模拟优化方法具有较高的计算效率。

4结论

本文将拉格朗日乘子法与子集模拟优化方法结合起来，发展了一种可用于结构优化设计的增广拉格朗日子集模拟优化方法，并利用两个工程算例对该方法的寻优能力和稳健性进行了验证。增广拉格朗日子集模拟优化方法是对原始子集模拟优化方法的改进与拓展，在求解多设计变量、多约束条件的结构优化设计问题上，具有更为优异的性能。

参考文献

[1] 李为吉， 宋笔锋， 孙侠生， 等. 飞行器结构优化设计[M]. 北京： 国防工业出版社， 2005.

LiWeiji,SongBifeng,SunXiasheng,etal.Aircraftstructureoptimization[M].Beijing:NationalDefenseIndustryPress, 2005.(inChinese)

[2]AdeliH,KumarS.Distributedgeneticalgorithmforstructuraloptimization[J].JournalofAerospaceEngineering, 1995, 8(3): 156-163.

[3]LiLJ,HuangZB,LiuF.Aheuristicparticleswarmoptimizationmethodfortrussstructureswithdiscretevariables[J].Computers&Structures, 2009, 87(7/8): 435-443.

[4]LambertiL.Anefficientsimulatedannealingalgorithmfordesignoptimizationoftrussstructures[J].Computers&Structures, 2008, 86(19/20): 1936-1953.

[5]KavehA,TalatahariS.Aparticleswarmantcolonyoptimizationfortrussstructureswithdiscretevariables[J].JournalofConstructionalSteelResearch, 2009, 65(8/9): 1558-1568.

[6]LeeKS,GeemZW.Anewstructuraloptimizationmethodbasedontheharmonysearchalgorithm[J].Computers&Structures, 2004, 82(9/10): 781-798.

[7]AuSK,BeckJL.Estimationofsmallfailureprobabilitiesinhighdimensionsbysubsetsimulation[J].ProbabilisticEngineeringMechanics, 2001, 16(4): 263-277.

[8]LiHS,AuSK.Designoptimizationusingsubsetsimulationalgorithm[J].StructuralSafety, 2010, 32(6): 384-392.

[9]LiHS.Subsetsimulationforunconstrainedglobaloptimization[J].AppliedMathematicalModelling, 2011, 35(10): 5108-5120.

[10]SedlaczekK,PeterR.UsingaugmentedLagrangianparticleswarmoptimizationforconstrainedproblemsinengineering[J].StructuralandMultidisciplinaryOptimization, 2006, 32(4): 277-286.

[11]RockafellarRT.ThemultipliermethodofHestenesandPowellappliedtoconvexprogramming[J].JournalofOptimizationTheory&Applications, 1973, 12(6): 555-562.

[12]JansenPW,PerezRE.ConstrainedstructuraldesignoptimizationviaaparallelaugmentedLagrangianparticleswarmoptimizationapproach[J].Computers&Structures, 2011, 89(13/14): 1352-1366.

[13]LongW,LiangXM,HuangYF,etal.AhybriddifferentialevolutionaugmentedLagrangianmethodforconstrainednumericalandengineeringoptimization[J].Computer-AidedDesign, 2013, 45(12): 1562-1574.

[14]CampCV,BichonBJ.Designofspacetrussesusingantcolonyoptimization[J].JournalofStructuralEngineering, 2004, 130(5): 741-751.

[15]PerezRE,BehdinanK.Particleswarmapproachforstructuraldesignoptimization[J].Computers&Structures, 2007, 85(19/20): 1579-1588.

[16]SchmitLA,MiuraH.Approximationconceptsforefficientstructuralsynthesis[J].AIAAJournal, 1976, 14(12): 692-699.

[17]GellatlyRA,BerkeL.Optimalstructuraldesign[R].FlightDynamicsLaboratory, 1971.

[18]GellatlyRA.Developmentofproceduresforlargescaleautomatedminimumweightstructuraldesign[R].FlightDynamicsLaboratory, 1966.

Augmented Lagrangian Subset Simulation Optimization Method

Dong Qiaoyue, Li Hongshuang

(College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:In solving the structural optimization problems with multiple design variables and multiple constraints, traditional optimization design method of engineering structure has many disadvantages. A new structural optimization method, which is based on subset simulation optimization(SSO) and the Lagrangian multiplier method, is developed to solve structural optimization problems under constraints. The Lagrangian multiplier method is used to handle multiple constraints. Then, SSO is used to solve the transformed unconstrained problem and search for the global optimum. In order to guarantee the robustness of convergence, the updating method of penalty factor is modified for this purpose. The accuracy, robustness and efficiency of the proposed method are demonstrated by two examples. The optimization results of proposed method are compared with those obtained by other optimization methods available in the literature. It indicates that the proposed method has excellent performance on searching for the global optimum.

Key words:structural optimization design; subset simulation optimization; Lagrangian multiplier method; penalty factor

收稿日期：2016-03-01；修回日期：2016-04-01

基金项目：国家自然科学基金(U1533109,11102084)

通信作者：李洪双,hongshuangli@nuaa.edu.cn

文章编号:1674-8190(2016)02-165-09

中图分类号：V214.19

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.02.005

作者简介：

董乔月(1991-)，男，硕士研究生。主要研究方向：飞行器结构设计、飞行器结构优化设计。

李洪双(1978-)，男，博士，副教授。主要研究方向：飞行器可靠性工程、飞行器结构优化设计。

(编辑：马文静)

江苏高校优势学科建设工程资助项目