基于流固耦合的燃机压气机叶片结构动力学分析
史久志,覃海起,尹洪,邓小文, 吕玉坤
(1.广东电网有限责任公司电力科学研究院,广东 广州 510080; 2.华北电力大学 能源与动力工程学院,河北 保定 071000)
基于流固耦合的燃机压气机叶片结构动力学分析
史久志1,2,覃海起1,尹洪1,邓小文1, 吕玉坤2
(1.广东电网有限责任公司电力科学研究院,广东 广州 510080; 2.华北电力大学 能源与动力工程学院,河北 保定 071000)
摘要:采用流固耦合的方法对某压气机转子叶片进行气动弹性数值模拟计算,将定常计算结果与实验结果进行对比,验证计算方法的正确性。在此基础上,采用单向流固耦合计算对叶片进行结构动力学分析,把非定常计算得出的气动力载荷转化为结构动力学分析中的载荷压力场形式,分析叶片在气动力作用下的瞬态响应,并进行模态分析。所得结果表明:叶片在气动力作用下承受较大的交变应力幅值,容易发生高周疲劳;产生了较大的动应力,最大应力值位于叶根前缘。通过分析叶片的各阶模态振型和危险点的位置,可以为叶片的疲劳设计分析提供依据,加强压气机转子叶片运行的安全可靠性。
关键词:流固耦合;气动力;瞬态响应;模态分析;高周疲劳
叶片高周疲劳引起的断裂故障是严重影响压气机设计质量和研制定型周期的关键问题之一[1-3],而作用在叶片上的气流扰动力是激发振动的最主要因素。因此,对压气机叶片的非定常气动力分析是很有必要的。
叶片在气流激振力作用下的动力响应问题比较复杂,它涉及到空气动力学和结构动力学内容。目前分析方法主要有:弱耦合法,包括时域的瞬态响应法和频域的稳态响应法[4];强耦合法,包括顺序耦合法和任意拉格朗日坐标系法[5-6]。
弓三伟等[7]借助CFX和ANSYS分析软件,采用单向顺序耦合法对某汽轮机末级大展弦比叶片进行了流固耦合计算,结果表明在非设计状态下流场对结构的变形具有更强的敏感性。徐可宁等[8]采用双向流固耦合法对某压气机叶片进行气动弹性数值计算,结果表明交替迭代算法是可行的,能得到叶片的瞬态响应,从而判断叶片是否发生颤振。张大义等[9]研究了某叶片的瞬态动力响应,指出叶片最大变形位于叶尖前缘,最大应力点位于叶根前缘。
本文以某压气机叶片为研究对象,首先采用CFX软件对流体域进行计算流体力学分析,提取叶片表面气体激振力结果,然后采用有限元分析软件ANSYS将该压力载荷加载到固体域表面,对其进行结构动力学分析,获得叶片的模态振型,并进行强度计算。最后对该转子进行双向流固耦合计算,研究叶片的振动特性,为叶片的设计和应用提供分析依据。
1基本控制方程及数值算法
本文对NASA Rotor67转子的单通道进行单向流固耦合和双向流固耦合计算,并对两种计算结果进行分析。
1.1流体动力学模型
本文计算采用的湍流模型为剪切应力输运(SSTκ-ω)模型[10]。SSTκ-ω模型是由Menter提出和发展的一种二方程湍流模型,其在近壁面边界层采用κ-ω模型,边界层边缘和自由剪切层采用κ-ε模型,通过系数叠加统一成κ-ω形式。跨声速压气机流场存在附面层分离、激波、二次流等复杂流动,近壁面压力分布的模拟结果直接影响到流固耦合计算的准确性,而该模型能够充分发挥κ-ω方程对于边界层流动计算和κ-ε方程对于自由剪切层计算的优势,进而保证流固耦合计算的准确性。
SSTκ-ω湍流模型方程为:
(2)
式中:κ为湍动能;ω为比耗散率;Γκ、Γω分别为κ和ω的有效扩散率;Gκ为平均速度梯度产生的湍动能;Gω为ω产生的湍流耗散率;Fκ、Fω分别为κ和ω的耗散项;Dω为横向耗散导数项;Sκ、Sω为源项;xi、xj都是变量;ρ为密度;νi为速度。
1.2结构动力学模型
多自由度系统动力学方程为
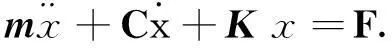
(3)
式中:m为质量矩阵;C为结构阻尼矩阵;K为刚度矩阵;x为位移矢量;F为力载荷量,如气动载荷、离心载荷等。
结构阻尼矩阵采用Rayleigh阻尼,表示为质量矩阵和刚度矩阵的线性组合,即
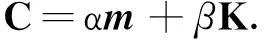
(4)
α和β是两个系数,可由两阶较重要的振型决定,取两阶振型阻尼比分别为ζ1和ζ2,动频分别为ω1和ω2,即
(5)
(6)
得出α和β后,可以确定任意第i阶振型的阻尼比
(7)
1.3流固耦合计算
1.3.1单向流固耦合计算
单向流固耦合计算不考虑变形叶片对流场的影响,流场计算得到的气动压力载荷在其内部进行迭代,当计算达到收敛容差后,把气动力加载到叶片上,得到了对应时刻下的叶片形变结果,再进行下一个时间步求解。本文研究叶片在气流激振力作用下的强迫响应,具体方法:将流场分析得到的叶片表面气动压力场分布结果加以处理,作为结构瞬态分析的力边界条件加载到有限元模型上,以此来求解叶片的瞬态响应。计算流程如图1所示。

图1 单向流固耦合计算流程
1.3.2双向流固耦合计算
双向流固耦合计算同时考虑了流场作用对固体结构的变形影响以及结构变形后对流场的反作用,结构变形改变了流体域的边界及耦合面上流体附面层的厚度和分离等。首先进行流体域求解,得到流场参数的分布结果,通过提取流体域耦合面上的压力载荷数据并将其加载至固体域的耦合面上,得到了该压力载荷下的固体形变结果,将固体结构变形后的节点位移反馈至流体域,修正流体域耦合面附近的网格后再次进行流场计算,如此反复求解。当流体域与固体域计算都达到收敛容差限后,再进行下一时间步的求解。计算流程如图2所示。
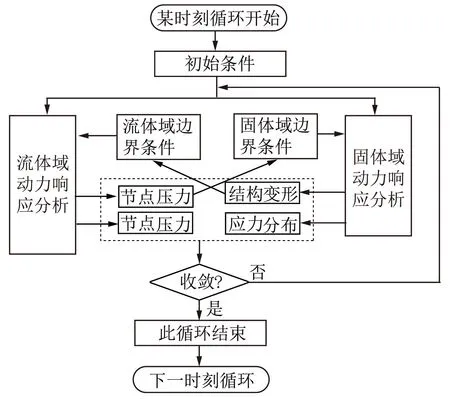
图2 双向流固耦合流程
2流固耦合数值模拟
2.1数值模拟
基于NASA Rotor67转子具有旋转周期对称性特性,选取转子全周区域的1/22(转子叶片有22个叶片)为研究对象,采用专业网格划分软件对流体域模型进行网格划分,网格节点数为63万,经网格无关性验证,该网格数量很好地兼顾了计算精度与计算时间的影响。叶片材料参数及压气机设计参数见表1。
表1材料参数和设计参数

名称数值杨氏模量E/Pa1.2×1011泊松比0.34密度ρ/(kg·m-3)4850转速n/(r·min-1)16043压比1.63
流场计算模型及叶片、轮毂表面网格分布如图3(a)所示。固体域单元类型选取8节点Solid 185单元,采用自由剖分四面体网格,单元总数为6 740个,节点总数8 218个,固体域计算网格如图3(b)所示。
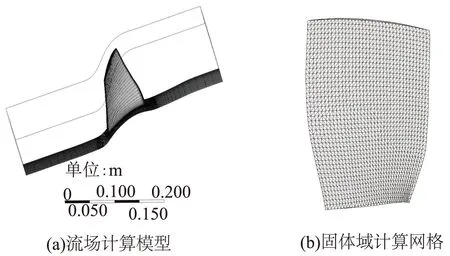
图3 流场及固体计算模型及网格
2.2计算方法的正确性验证
对NASA Rotor 67转子湍流SSTκ-ω模型做定常计算,计算参数设置见表2。
表2计算设置参数

名称数值时间步长/s1.7×10-5总时间/s0.017进口总温度T/K288进口总压pi/kPa101.325出口平均静压po/kPa115.325
将定常计算结果与NASA报告[11]中的实验结果进行对比分析,所得结果见表3。
表3定常计算结果与实验结果对比

名称计算值实验值相对误差/%质量流量/(kg·s-1)33.6633.660压比1.611.63-1.2绝热效率0.880.8780.2
由表3可知,在近设计工况下,定常计算结果与实验结果相对误差较小,结果符合良好,证明采用的计算模型和方法是可行的。
3叶片结构动力学分析
3.1模态分析
叶片根部采用固支约束,分别计算叶片的静频和在预应力作用下的动频,所得结果见表4。
表4叶片前6阶静频和动频计算结果

阶数静频/Hz动频/Hz振型1675.47764.33一阶弯振21832.11930.7二阶弯振32467.42496.9一阶扭转44075.04140.9复合振动55125.95195.9二阶弯扭66045.46116.5复合振动
将离心载荷加载到叶片的每个节点单元上,同时将气动力以预应力的形式加载到叶片表面每个网格节点上,得到叶片的固有频率和相应的模态振型,分析各阶振型下叶片的振动情况。图4为叶片的前六阶模态振型。

图4 叶片的前6阶振型
关注叶片前两阶的频率,提取前两阶的动频,求得Rayleigh阻尼系数分别为0.000 50、0.000 52, 依次将其带入方程(7)得到各阶的阻尼比。
由表4及图4可知,在气动力和离心力载荷作用下,叶片的固有频率变大。叶片第一阶和第二阶的振动形式为弯曲振动,第三阶振动形式为一阶扭转振动,第四、第五、第六阶振动形式为弯曲和扭转的复合振动。当叶片处于各阶共振模态时,随着共振阶次的增加,振动形式越来越复杂。
3.2单向流固耦合计算及强度分析
如何将非定常计算得到的气动压力分布数据转化成适合于结构动力学分析中的压力载荷形式并引入有限元分析,是强度计算中的一个难题。在ANSYS瞬态分析中,压力或者任何其他形式的表面力都不能直接加载到叶片单元节点上,因此必须把气动计算结果作一定形式的转化。本文首先在固体域表面创建一层面单元,将非定常计算得到的压力载荷输出到面单元的每个节点上,再以预应力的形式加载到叶片的每个单元上,分析叶片在某一时刻的强迫响应。
图5(a)为某一时刻面单元在流场中的模型,利用该面单元提取激振力并将其加载到叶片表面单元上;图5(b)为某一时刻叶片在气动力作用下的压力分布云图。

图5 面单元模型及叶片压力分布云图
在气动力的作用下,叶片会产生位移响应。t时刻叶片的位移、应力分布如图6所示。

图6 叶片的位移分布云图及应力分布云图
从图6可看到,t+nΔt为叶片位移和应力最大时对应的时刻。此时叶片最大位移为1.683 mm,位于叶尖前缘处,最大应力为354 MPa,位于叶根前缘处,如图6(a)所示。将图6(a)与图4中的模态振型进行对比可以看出,叶片的振动形式是一阶弯曲振动,最大位移发生在叶尖前缘处,沿径向逐渐减小,转子叶片在气动力作用下承受较大的交变应力幅值如图6(b)所示,容易发生高周疲劳;转子叶片在气流压力波动下产生了较大的动应力,最大应力值位于叶根前缘。通过分析叶片危险点的位置,可以为疲劳设计提供依据。
3.3双向流固耦合计算
通过双向流固耦合计算,可获取叶片在流场中的振动特性。在叶片表面近壁区选取6个监测点来监测叶片关键点的振动位移,节点分别为叶尖T1、T2、T3和叶片中部(M1、M2、M3点)共6个点,分布如图7所示。由于压力面和吸力面对应网格节点的位移基本相同,因此在弦向上只选取压力面上的节点进行监测。
图7 监测点的位置示意图
图8为双向流固耦合计算在近设计工况下得到的叶片关键点位移响应曲线。图9为叶片在近失速工况下关键点的位移响应曲线,时间步长设置为5.667×10-6s。
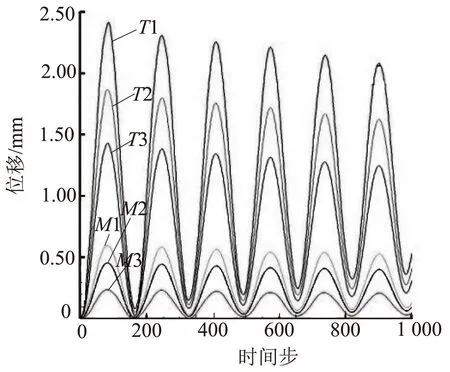
图8 叶片在近设计工况下关键点的位移响应曲线

图9 叶片在近失速工况下关键点的位移响应曲线
从图9可以看出,叶片在阻尼作用下,各个监测点的振动周期一致,振幅随时间逐渐减小趋于某一定值,通过各个测点最后的位移可以描绘出叶片的形状,得出叶片的振动频率为356.8 Hz,远小于叶片的固有频率,表明该工况下叶片不会发生共振。
4结论
a) 对压气机转子叶片进行分析,证明采用流固耦合计算方法对叶片进行气动弹性数值模拟可行。
b) 分析了叶片在预应力作用下的各阶振型,当叶片处于各阶共振模态时,随着共振阶次的增加,振动形式越来越复杂。
c) 采用流固耦合计算,可以获得不同时刻由气动力激振引起的叶片动应力分布,进一步进行结构动力学分析,得到叶片的瞬态位移响应和应力响应,可以确定叶片的振动形式以及该工况下应力集中的位置,作为进一步分析的依据。通过双向流固耦合计算,可以得到叶片位移响应曲线,在叶片阻尼的作用下,叶片的振动位移幅值随时间逐渐减小。
参考文献:
[1] SRINIVASAN A V. Flutter and Resonant Vibration Characteristic of Engine Blades[J]. Engineering for Gas Turbines and Power, 1997, 119(8): 742-775.
[2] KULKARNI A, TISSERANT D, HOSNY D. Turbine Wheel High Cycle Fatigue Reliability Prediction[C] //Proceedings of ASME Turbo Expo 2010. London: ASME, 2010:171-181.
[3] 宋兆泓,陈光,张景武,等.航空发动机典型故障分析[M]. 北京:北京航空航天大学出版社,1993.
[4] SHIPMAN W C, PALA ZOTTO A N. The Consideration of High Cycle Fatigue in a Turbine Blade [R]. Washington D.C.:AIAA, 2002.
[5] HIRT C W, AMSDEN A A, COOK J L. An Arbitrary Lagrangian-eulerian Computing Method for All Flow Speeds[J]. Journal of Computational Physsics, 1974(14): 227-253.
[6] RAMMAKRISHNAN K, LAWLESS P B, FLEETER S. Finite Element Simulation of Turbo Machine Blade Row Viscous Interactions Vane Vibratory Stress Predictions[R]. Washington D.C.:AIAA,2004.
[7] 弓三伟,任丽芸,刘火星,等.汽轮机末级转子叶片流固耦合计算[J]. 热力透平,2007,36(3):154-157.
GONG Sanwei, REN Liyun, LIU Huoxing, et al. Fluid Solid Interaction of Rotor Blade in Last Stage of Steam Turbine[J]. Thermal Turbine, 2007, 36(3): 154-157.
[8] 徐可宁,王延荣.压气机转子叶片的气动弹性数值模拟[J]. 航空动力学报,2010,25(10):2206-2210.
XU Kening, WANG Yanrong. Numerical Simulation of Aero-elastic Response in Compressor Rotor blades[J]. Journal of Aerospace Power, 2010,25(10):2006-2010.
[9] 张大义,马艳红,洪杰.气流激励下叶片动力响应分析方法[J]. 航空动力学报,2009,24(7):1523-1527.
ZHANG Dayi, MA Yanhong, HONG Jie. Dynamical Response Analysis on Blades Arisen by Aerodynamic Forces Through Sequential Method [J]. Journal of Aerospace Power, 2009, 24(7):1523-1527.
[10] MENTER F R. Two Equation Eddy Viscosity Turbulence Models for Engineering Applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.
[11] STRAZISAR A J, WOOD J R, HATHAWAY M D, et al. Laser Anemometer Measurements in a Transonic Axial-flow Fan Rotor [R]. Washington D.C.:NASA,1989.
Structural Dynamics Analysis on Gas Turbine Compressor Blade Based on Fluid-solid Coupling
SHI Jiuzhi1,2, QIN Haiqi1, YIN Hong1, DENG Xiaowen1, LÜ Yukun2
(1. Electric Power Research Institute of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510080, China; 2. School of Energy and Power Engineering, North China Electric Power University, Baoding, Hebei 071000, China)
Abstract:Fluid-solid coupling method is used for numerical simulating calculation on aeroelasticity of rotor blades of some compressor, and result of steady-state computation and experimental result are compared to verify veracity of this computation method. By means of one-way fluid-solid coupling calculation, this paper carries out structural dynamics analysis on blades which is to transfer aerodynamic load obtained from unsteady computation to the form of load pressure field for structural dynamics analysis. It analyzes transient response of blades under aerodynamic force and conducts modal analysis as well. Results indicate that blades may bear larger amplitude of alternating stress under aerodynamic force and be easy to produce high-cycle fatigue. In addition, larger dynamic stress is produced and the maximum stress occurs at the leading edge of blade root. Analysis on modal shape of each order and locations of dangerous points may provide basis for design and analysis on fatigue of blades as well as strengthen operational security and reliability of blades.
Key words:fluid-solid coupling; aerodynamic force; transient response; modal analysis; high-cycle fatigue
收稿日期:2016-01-22
基金项目:中国博士后科学基金面上资助项目(2015M570696);中国南方电网有限责任公司科技项目(GDKJ00000005)
doi:10.3969/j.issn.1007-290X.2016.05.001
中图分类号:V232.4
文献标志码:A
文章编号:1007-290X(2016)05-0001-05
作者简介:
史久志(1990),男,河南商丘人。在读硕士研究生,主要从事燃气轮机等发电设备研究工作。
覃海起(1990),男,广西柳州人。在读研硕士研究生,主要从事压气机稳定性研究。
尹洪(1987),男,重庆人。在站博士后,工学博士,主要从事燃气轮机等发电设备研究工作。
(编辑王夏慧)

