局部耦合双回输电线路故障分析计算方法

王维航，杜婉琳，梁远升

(华南理工大学 电力学院，广东 广州 510641)

局部耦合双回输电线路故障分析计算方法

王维航，杜婉琳，梁远升

(华南理工大学 电力学院，广东 广州 510641)

摘要：受耦合部分线路间互感的影响，现有的针对完全同塔的故障分析方法不再适用。为此，针对局部耦合双回输电线路的故障分析展开研究。根据局部耦合同塔双回输电线路的结构和特点，利用相分量法和端口网络理论建立局部耦合双回输电线路各区段方程，结合故障边界条件方程,实现了一种针对局部耦合双回输电线路的故障计算方法。最后，利用电磁暂态仿真软件ATP-EMTP构建局部耦合同塔双回输电线路模型并进行仿真验证，结果表明所提方法计算误差小，且不受过渡电阻和故障类型的影响。

关键词：局部耦合；同塔双回输电线路；故障分析；相分量法；端口网络理论

随着经济发展，架空线路走廊资源日益紧张，成为限制电力行业发展的制约因素。而同塔多回架设输电线路具有降低经济成本，提高土地利用率等特点，因此得到了广泛的应用[1]。然而，受架设时间和供电区域不同等因素的影响，全程同塔架设的线路应用较少，大多数同塔多回输电线路采用部分同塔方式建设。相比于全线同塔多回输电线路，局部耦合线路线间的互感耦合更加复杂，已有的针对全线同塔线路故障分析方法无法应用于这类结构。因此，对局部耦合线路故障分析方法进行研究具有重要意义。现有的故障分析方法主要有序分量法[2-6]和相分量法[7-13]。序分量法通过变换将耦合的相分量转换成无耦合的序分量，然后根据故障边界条件将各序网连成复合序网图进行故障计算。但由于同塔多回输电线路故障种类繁多，复合序网图的连接较为复杂，故很难形成一种通用的计算方法。而相分量法是根据各元件模型以各相电气量为基础构建方程，能直观准确的反应电力网络的问题，故较适用于局部耦合输电线路的故障分析。

随着同塔双回线路的增多，同塔输电线路成为专家学者的研究重点，针对同塔双回输电线路的故障分析方法陆续的被提出[2-11]。文献[3]讲述了如何用12序分量法对同电压等级下的完全同杆四回线进行故障计算，并用电磁暂态程序(electro-magnetictransientprogram，EMTP)验证了所提计算方法的准确性。文献[8]提出了一种虚拟网络加网络操作法的双回线故障计算方法，该方法不受故障类型的影响具有统一的计算模型；且无需形成复合序网，既适用于序坐标也适用于相坐标。但上述方法均以全程同塔线路为研究对象，现有针对部分同塔双回输电线路的故障分析方法的研究较少，若将传统故障分析方法应用于局部耦合线路的故障计算，由于其忽略局部耦合的影响，会产生较大误差，无法满足部分同塔线路的故障计算要求。文献[14]对不同电压等级部分耦合线路的单回线故障分析进行了研究，提出了一种改进的解耦序分量法。但是，并未对跨线故障进行故障分析且仅研究了两端无公共母线的线路模型。

为此，本文针对一端有公共母线的局部耦合双回输电线路故障分析方法展开了研究。根据局部耦合双回输电线路的结构和特征，利用变换矩阵对同塔段线路进行解耦，并将相分量法与端口网络理论相结合，建立了线路各段电压和电流接口方程。在此基础上，结合不同故障情况下的故障边界条件，构建出局部耦合双回输电线路故障计算方程组进行计算。最后利用ATP-EMTP软件搭建仿真模型，对所提故障分析方法的正确性进行验证。

1局部耦合双回输电线路线路方程

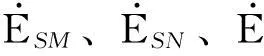
图1　三端系统局部耦合同塔双回输电线路模型

图1中，整个线路模型可看成由各段线路经母线和耦合分界点连接而成，故可用相分量法对每段列写方程，并通过端口网络理论将各段方程联系起来。输电网络中主要有三类线路模型：电源侧线路、双回耦合输电线路以及单回输电线路。

a) 电源侧输电线路。以电流流出电源方向为正方向，以SM段为例，其电压电流关系如下：

(1)

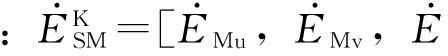
对于SN、SP段采用同样的方法可得：

(2)

(3)

b) 局部耦合部分MD段。由于双回线间存在线间耦合，需对其进行解耦。本文采用文献[1]所给出的平行双回线相模变换矩阵及反变换矩阵对其进行解耦：

(4)

利用式(4)对MD段解耦可得式(5)，双回线的各向量被分解为两个无线间互感的向量，从而消除线间互感。

(5)

其中：

式中：ZMDS为MD段双回线单位自感；ZMDm为单位相间互感；ZMDx为双回线之间的单位互感。

c) 单回输电线路。以DN段为例，其电压电流关系如下：

(6)

对于DP、NP段采用同样的方法可得：

在M、N、P三点，均有三条输电线路通过，根据基尔霍夫电流定律可得：

(9)

至此，线路各区段方程均列出，联立式(1)—式(3)，式(5)—式(9)，对方程组进行求解，即可求出各节点各相电压电流值。

2局部耦合双回输电线路短路电流计算

局部耦合双回输电线路的故障主要分为两类：耦合段线路故障和单回线路故障，分别如图2(a)和 (b)所示。当短路故障发生时，线路的结构发生了变化，新增了故障节点F，故针对原有结构列写的方程组需改写。

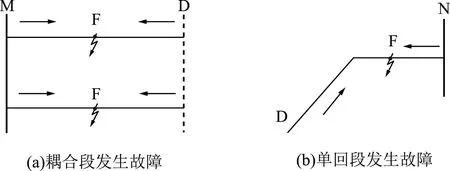
图2　短路故障示意图

2.1耦合双回线路故障计算

根据图2(a)所示，故障发生在耦合段时，可将耦合段拆分成两段分别列写方程组。以MD发生故障为例，采用式(4)分别对MF段和DF段电压电流方程解耦，可得：

(11)

由式(10)和(11)可知，由于故障节点的增加，根据故障后的线路结构列写的方程组增加了故障点电压和电流等未知量，故需根据故障类型添加故障边界条件方程，使方程数等于未知量个数，从而求解各节点电压电流量。

若耦合段MD上I回线发生U、V两相短路接地故障，接地过渡电阻为Rg，则其故障边界条件为：

(12)

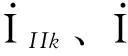
联立式(1)—式(3)，式(6)—式(12)，使方程数与未知数数量相等，从而可以求解线路各节点电压电流量。

2.2单回线路故障计算

如图2(b)所示，当故障发生在单回段时，也可将故障线路拆成两段线路列写方程组。以DN段F点发生故障为例，则有：

(13)

若耦合段ND上发生U相短路接地故障，则其故障边界条件为：

(14)

联立式(1)—式(3)、式(8)—式(11)、式(14)和式(15)使方程数与未知数数量相等，从而可以求解线路各节点电压电流量。

2.3无环网局部耦合故障计算

本文所提方法对不同结构的部分同塔局部耦合双回输电线路均适用。图3为三端局部耦合同塔双回输电线路模型，与图1所示模型相比，此模型N、P端无电气连接。

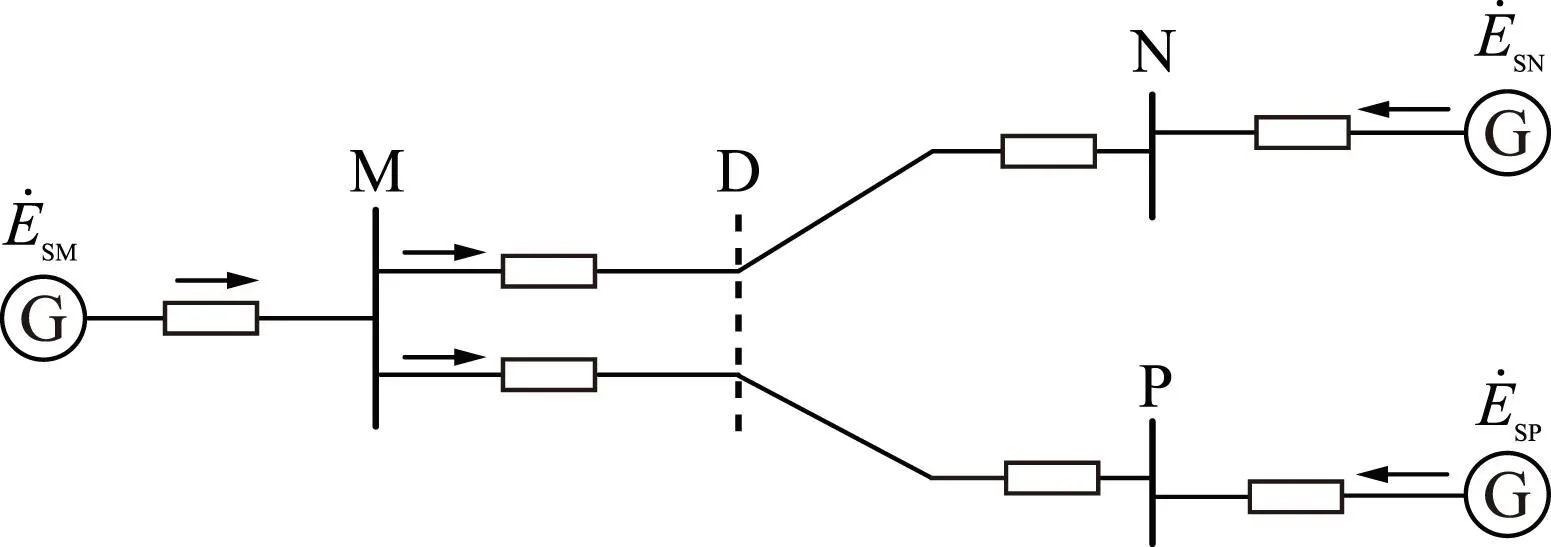
图3　无环网局部耦合同塔双回输电线路模型

3仿真分析及验证

设图1中MD中点处分别发生金属性接地故障和接地过渡电阻Rg=50Ω的故障，表1和表2给出了几项典型的故障的计算结果与仿真结果的比较。同时，设图3所示结构距M端80km处发生金属性短路故障，表3给出了计算结果与仿真结果的比较。

由表1可见，在金属性接地故障时，采用本文所提故障分析方法与仿真结果比较，最大绝对误差为0.042kA；由表2可见，当接地故障电阻为50Ω时，最大绝对误差为0.023kA；由表3可见，最大绝对误差为0.046kA；且各种故障情况下相对误差均在1%之内。由此可见，计算值与仿真结果相近，从而证明了所提方法的有效性及计算结果的精确性。

表1MD耦合段中点金属性接地故障

故障类型故障相计算值/kAEMTP仿真值/kA绝对误差/kA相对误差/%IUGIU7.6167.5740.0420.554IVWGIV14.11514.1020.0130.092IW14.30914.2960.0130.091IUIIVWGIU15.99215.9830.0090.056IIV16.21416.2000.0140.086IIW16.43516.4240.0110.067IUVIIVWGIU17.93117.9280.0030.017IV11.96111.9390.0220.184IIV11.96111.9390.0220.184IIW18.09318.0860.0070.039IUVWIIUVGIU13.65813.6420.0160.117IV13.96513.9490.0160.114IW18.91618.9110.0050.026IIU13.65813.6420.0160.117IIV13.96513.9490.0160.114IUVWIIUVWGI回14.89214.8800.0120.081II回14.89214.8800.0120.081

注：故障类型IUG表示在I回线U相发生接地故障，IUIIVWG表示在I回线U相和II回线V、W两相同时发生接地故障，其余故障类型表示方法与此类似，下同。

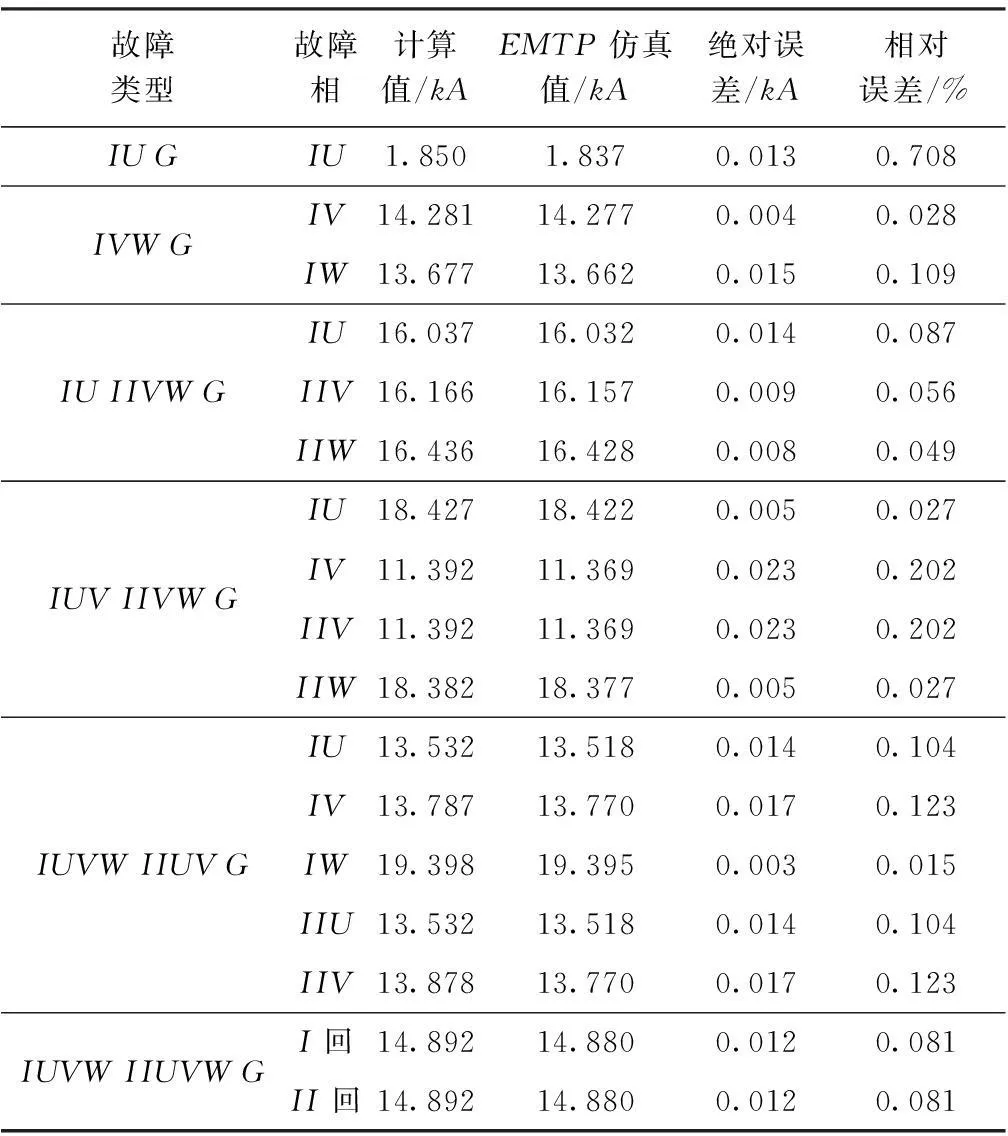
表2　MD耦合段中点存在50 Ω过渡电阻接地故障

表3距M端80km金属性接地故障

故障类型故障相计算值/kAEMTP仿真值/kA绝对误差/kA相对误差/%IUGIU5.4915.4450.0460.845IVWGIV9.1309.1100.0200.219IW9.3149.2850.0290.312IUIIVWGIU10.07910.0530.0260.259IIV10.53910.5160.0230.219IIW10.80910.7910.0180.167IUVIIVWGIU11.62711.6040.0230.198IV7.7777.7450.0320.413IIV7.7777.7450.0320.413IIW11.81311.7910.0220.187IUVWIIUVGIU8.9048.8790.0250.282IV9.2899.2640.0250.269IW12.35712.3380.0190.154IIU8.9048.8790.0250.282IIV9.2899.2640.0250.269IUVWIIUVWGI回9.8649.8400.0240.244II回9.8649.8400.0240.244

4结束语

本文针对部分同塔双回输电线路进行故障分析，根据输电线路结构，利用解耦理论及端口网络理论，提出了一种故障分析方法，此方法在不同故障类型下均保持较高计算精度，且不受过渡电阻的影响，此方法对拓展局部耦合双回输电线路的继电保护研究具有积极意义。

参考文献：

[1] 葛耀中．新型继电保护与故障测距原理与技术[M]. 西安：西安交通大学出版社，1996.

[2]FUNABASHIT，OTOGUROH，MIZUMAY，etal．DigitalFaultLocationforParallelDouble-circuitMultiTerminalTransmissionLines[J].IEEETrans.onPowerDelivery，2000，15(2)：531-537.

[3] 田羽，范春菊，龚震东．同杆4回线12序分量法[J]. 电力系统自动化，2007，31(21)：35-39.

TIANYu，FANChunju，GONGZhendong．Twelve-sequenceComponentMethodofFour-parallelLinesonSameTowers[J].AutomationofElectricPowerSystems，2007，31(21)：35-39.

[4] 刘玲，范春菊．基于六序分量法的跨电压等级的同塔四回线的故障计算[J]. 电力系统保护与控制，2010，38(9)：6-11.

LIULing，FANChunju．FaultCalculationforJointFourTransmissionLinesofDifferentVoltageGradesontheSameTowerBasedonSix-sequence-componentMethod[J].PowerSystemProtectionandControl，2010，38(9)：6-11.

[5] 范春菊，舒巧俊．序分量法在电力系统中的应用[J]. 电气电子教学学报，2010，32(5)：32-36，46.

FANChunju，SHUQiaojun．ApplicationofSequenceComponentMethodinPowerSystem[J].JournalofElectrical&ElectronicEducation，2010，32(5)：32-36，46.

[6] 邓孟华，范春菊，刘玲，等．基于12序分量的同杆4回线短路故障计算[J]. 电力系统自动化，2008，32(14)：64-67.

DENGMenghua，FANChunju，LIULing，etal．CalculationofShortCircuitFaultofFourJointedParallelLinesontheSameTowerBasedonTwelveSequenceComponents[J].AutomationofElectricPowerSystems，2008，32(14)：64-67.

[7] 王安宁，陈青，周占平．改进的相分量法求解电力系统复杂故障新算法[J]. 电力系统自动化，2008，32(18)：39-43.

WANGAnning，CHENQing，ZHOUZhanping．AnImprovedPhaseComponentsMethodforArbitraryComplicatedPowerSystemFaultAnalysis[J].AutomationofElectricPowerSystems，2008，32(18)：39-43.

[8] 曹国臣，张洪波．采用虚拟网络加网络操作法的双回线故障计算方法[J]. 中国电机工程学报，2006，26(2)：71-77.

CAOGuochen，ZHANGHongbo，AUnifiedMethodtoCalculateFaultsinDoubleCircuitTransmissionLinesBasedonFictitiousNetworkPlusNetworkOperationMethod[J].ProceedingsoftheCSEE，2006，26(2)：71-77.

[9] 王安宁，陈青，周占平，等．改进的相分量法求解同杆双回线故障新算法[J]. 电力系统自动化，2009，33(13)：58-62.

WANGAnning，CHENQing，ZHOUZhanping，etal．AnImprovedPhaseComponentMethodforCalculatingFaultsontheDouble-circuitTransmissionLinesonSameTower[J].AutomationofElectricPowerSystems，2009，33(13)：58-62.

[10] 刘为雄，蔡泽祥，邱健．融合对称分量法与相分量法的大规模电力系统跨线故障计算[J]. 电工技术学报，2007，22(5)：140-145.

LIUWeixiong，CAIZexiang，QIUJian．Inter-lineFaultCalculationUsingIntegratedSymmetry-componentandPhase-ComponentMethodforLargeScalePowerSystem[J].TransationsofChinaElectrotechnicalSociety，2007，22(5)：140-145.

[11] 刘为雄，蔡泽祥．基于相分量法的电力系统复故障计算[J]. 电力系统及其自动化学报，2007，19(3)：91-95.

LIUWeixiong，CAIZexiang．SimultaneousFaultCalculationforPowerSystembyPhaseCoordinates[J].ProceedingsoftheCSU-EPSA，2007，19(3)：91-95.

[12] 张云鹏，季田，魏华勇. 复杂结构输电线路接地短路及光纤复合架空地线电流计算[J].电力系统自动化，2015，39(16):132-137.

ZHANGYunpeng，JITian，WEIHuayong.AnalysisandCalculationofFaultCurrentforOptical-fiberCompositeOverheadGroundWireinPowerSystemFaultofComplexTransmissionLine[J].AutomationofElectricPowerSystems，2015,39(16):132-137.

[13] 许红断，周云海，胡翔勇，等. 浅谈电力系统复杂故障计算方法[J]. 河北工程技术高等专科学校学报，2004(4):26-29.

XUHongduan,ZHOUYunhai,HUXiangyong,etal.TheMethodofCalculationofComplexFaultinPowerSystem[J].J.ofHebeiEngineeringandTechnicalCollege，2004(4):26-29.

[12] 许侃，范春菊．不同电压等级部分耦合线路的单回线故障分析[J]. 电力系统自动化，2015，39(12):81-87.

XUKan，FANChunju．LineFaultAnalysisonParticalCouplingLinesatDifferentVoltageLevels[J].AutomationofElectricPowerSystems，2015，39(12)：81-87.

AnalysisandCalculationMethodforFaultofPartialCouplingDouble-circuitPowerTransmissionLines

WANGWeihang,DUWanlin,LIANGYuansheng

(ElectricPowerCollegeofSouthChinaUniversity,Guangzhou,Guangdong510641,China)

Abstract：Existing fault analysis method for double-circuit power transmission lines on the same tower is not applicable any more due to influence of mutual inductance among coupling lines. Therefore, this paper studies fault analysis on partial coupling double-circuit power transmission lines. According to structures and characteristics of partial coupling double-circuit transmission lines, sector equations for partial coupling double-circuit power transmission lines are established by using phase component method and port network theory. A kind of fault calculation method for partial coupling double-circuit power transmission lines is realized by combining fault boundary condition equation. Finally, electromagnetic transient simulation software ATP-EMTP is used for constructing a model for emulation proof and the result indicates that the proposed method has small errors in calculation and is not affected by transition resistance and fault types.

Key words：partial coupling; double-circuit power transmission line on the same tower; fault analysis; phase component method; port network theory

收稿日期：2016-01-06

基金项目：国家自然科学基金项目(51307065)；中央高校基本科研业务费专项资金(2013ZZ028)

doi:10.3969/j.issn.1007-290X.2016.05.018

中图分类号：TM855

文献标志码：A

文章编号：1007-290X(2016)05-0097-05

作者简介：

王维航(1991)，男，黑龙江大庆人。在读硕士研究生，主要研究方向为电力系统同塔多回线故障分析。

杜婉琳(1993)，女，广东潮州人。在读硕士研究生，主要研究方向为电力系统同塔多回线故障测距。

梁远升(1980)，男，广东广州人。副教授，工学博士，主要研究方向为电力系统故障分析与故障测距。

(编辑王朋)