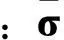基于混合高斯模型的配电网负荷伪量测权重优化算法

申定辉，于晓蕾，吴丹

(1.国网安徽省电力公司六安供电公司，安徽 六安237000；2.国网安徽省电力公司众兴电力设计院有限公司，安徽 合肥230000；3.国网江西省电力公司南昌供电公司，江西 南昌330000)

基于混合高斯模型的配电网负荷伪量测权重优化算法

申定辉1，于晓蕾2，吴丹3

(1.国网安徽省电力公司六安供电公司，安徽 六安237000；2.国网安徽省电力公司众兴电力设计院有限公司，安徽 合肥230000；3.国网江西省电力公司南昌供电公司，江西 南昌330000)

摘要：提出一种基于高斯混合模型(Gaussian mixture model，GMM)的配电网负荷量测权重优化算法，包括对GMM参数的优化和权重确定。首先采用引力搜索算法(gravitational search algorithm，GSA)对数据的最佳聚类个数进行判断，利用K-means算法获取数据的初始聚类中心、方差和混合权重；然后通过组合马尔科夫链蒙特卡洛期望最大化(Markov chain Monte Carlo-expectation maximum, MCMC-EM)算法对GMM的参数进行估计；最后根据优化的GMM，提出负荷伪量测权重优化方法，确定负荷伪量测的权重。以改进IEEE-12节点系统对所提方法进行验证，结果表明其合理、有效。

关键词：配电网；状态估计；伪量测权重；高斯混合模型；组合马尔科夫链蒙特卡洛期望最大化算法

近年来，分布式电源的大量接入使得配电侧的状态估计研究迎来了全新的机遇和挑战。状态估计作为未来构建配电管理系统(distribution management system，DMS)的底层核心应用，起到了关键的作用，但也面临着一定的问题，如配电网实时量测有限，低压用户的负荷没有实时量测等。研究指出，可以利用用户的负荷数据作为状态估计的伪量测，但人为设定的30%～50%的量测可信度存在不合理、与实际情况不符等问题，影响状态估计的准确性。负荷伪量测的权重与负荷本身的统计特性有很大的关系，所以充分利用用户负荷历史数据对负荷数据的统计特性进行研究，从而更好地确定负荷量测的权重，是十分重要和有意义的。

负荷建模通常采用高斯分布[1]的方法，但单一的高斯分布不能适应所有的负荷。文献[2]通过统计方法对负荷数据进行分析，认为电力负荷变化的统计特性不符合任何常见的概率分布函数。文献[3-7]通过不同的概率分布模型对负荷进行建模。Irwin等人[3]提出使用Weibull分布模型拟合消费结算数据，虽然分布足够灵活，能够很好地拟合北爱尔兰的能源消耗分布，但仅涵盖用户的计费数据；Seppala[4]建议采用对数正态分布模型；Herman和Kritzinger[5]对电网的负荷进行不同分布函数的拟合，并指出β分布具有较好的拟合性；在配电网状态估计问题中，Ghosh等人[6]作了类似的研究，通过卡方分布验证了正态分布、对数正态分布和β分布对测试数据的拟合性，指出系统对β分布具有明显的偏好，因为β分布具有很好的灵活性以及对分布偏度的适应性；文献[7]提出一种改进的β分布模型，但β分布对波动较大的负荷拟合性较差，且不能很好地嵌入基于最小二乘准则的状态估计程序中。文献[8]提出一种新的量测权重确定原则，但该原则仅针对输电网状态估计中关键的实时量测。

由以上分析可以得出，没有独特的方法能够模拟负荷的概率密度函数。一般情况下，负荷曲线的高斯模型因其简单和能够通过2种参数(均值、方差)来描述，许多计算工具(例如状态估计目标函数)可以很容易地嵌入高斯概率密度函数中，使得高斯模型成为负荷建模的很好选择。由前文可知，单一的高斯分布不能满足所有负荷分布的要求，而高斯混合模型(Gaussian mixture model，GMM)[9]为这一问题提出了解决方法。期望最大化(expectation maximum，EM)算法[10]是GMM参数估计的很好选择，在实际应用中，因在积分和求导上存在计算问题，常常采用近似算法估计模型参数。

基于以上分析，本文提出基于GMM的配电网负荷伪量测权重优化方法，采用组合马尔科夫链蒙特卡洛期望最大化(Markov chain Monte Carlo-expectation maximum, MCMC-EM)[12]算法优化GMM的组合参数，采用优化算法对负荷权重进行优化。以某电网的母线负荷曲线对所提算法进行分析，并通过改进IEEE-12节点系统验证所提方法的合理性和有效性。

1GMM与状态估计模型

1.1GMM

GMM是若干个服从高斯分布函数并通过有限加权获得的概率密度分布函数，其特性由M个高斯分布的均值、方差确定。GMM的数学表达式为

其中

1.2状态估计模型

在状态估计中，量测量z与状态量x之间的关系为

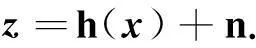
式中：n为量测噪声，h为量测函数。

最小二乘法状态估计目标函数和约束条件为：

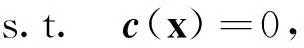
式中：J(x) 为状态估计目标函数，r为量测值与计算值之间的误差值，c(x)为约束条件，R为量测量权重矩阵。

在配电网中，负荷伪量测的误差大，统一设定为一个值不符合实际情况。本文通过建立负荷的GMM来计算负荷伪量测的权重，从而使计算结果更接近实际。

2基于组合MCMC-EM算法的GMM参数优化

组合MCMC-EM算法主要由3部分组成：基于引力搜索算法(gravitational search algorithm，GSA)[11]的数据最佳聚类分析；基于K-means算法的初始均值、方差和混合权重的确定；基于MCMC-EM算法的GMM参数确定。本文的K-means算法使用矩阵实验室(Matrix Laboratory，MATLAB)内嵌函数。

2.1GSA

设聚类个数为k，数据的聚类离散度为W(k)，参考分布集Wr(k)的平均值为E[lnWr(k)]，GSA的基本思想是通过比较数据集每次聚类的E[lnWr(k)]和lnW(k)来判断最佳聚类个数。GSA定义了k个聚类的间隙值

其中：

式中：|ca|为第a个聚类的数据个数，Da为第a个聚类中数据点间的距离之和，n为聚类的个数，F为参考分布集的组数，Wr,j(k)为参考分布集的第j个元素。

通过间隙量Hgap(k)来确定最佳聚类个数，判断公式为

(1)

式中sk+1为E[lnWr(k)]的标准差。

若聚类数k满足式(1)，则k为最佳聚类个数。

2.2MCMC-EM算法

MCMC-EM算法的步骤：

c)在q+1次迭代时，计算第t个加权权重

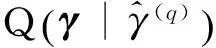
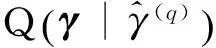
f)估计误差。若第j个样本的期望值

第j个样本的方差

g)取子取样的时刻tk。

i)对每一个j=1,...,m ，计算

其中

j)重复步骤c)至步骤i)直至收敛，收敛条件为

式中Lq为第q次迭代的极大似然函数。

3基于GMM的负荷权重优化

若根据MCMC-EM算法确定的配电网母线ρ的负荷GMM

则集合

式中：xρ(t)为时刻t母线ρ的负荷值，σj为第j个伪量测误差。

根据满足式(2)的Sρ(t)个数的不同，设定以下准则对负荷xρ(t)的权重进行确定：准则一，若满足式(2)的Sρ(t)唯一，则量测权重Rρ(t)=(uj/σj)2；准则二，若满足式(2)的Sρ(t)不唯一，则通过高斯分布重新进行优化组合。准则二的优化步骤如下：

a) 选取最大的组成成分为主要成分，并设置为wp,其期望值为up，方差为Σp。

b) 定义第j个量测距离

c) 通过卡方分布进行检验，设定99%的置信区间，形成阈值T。

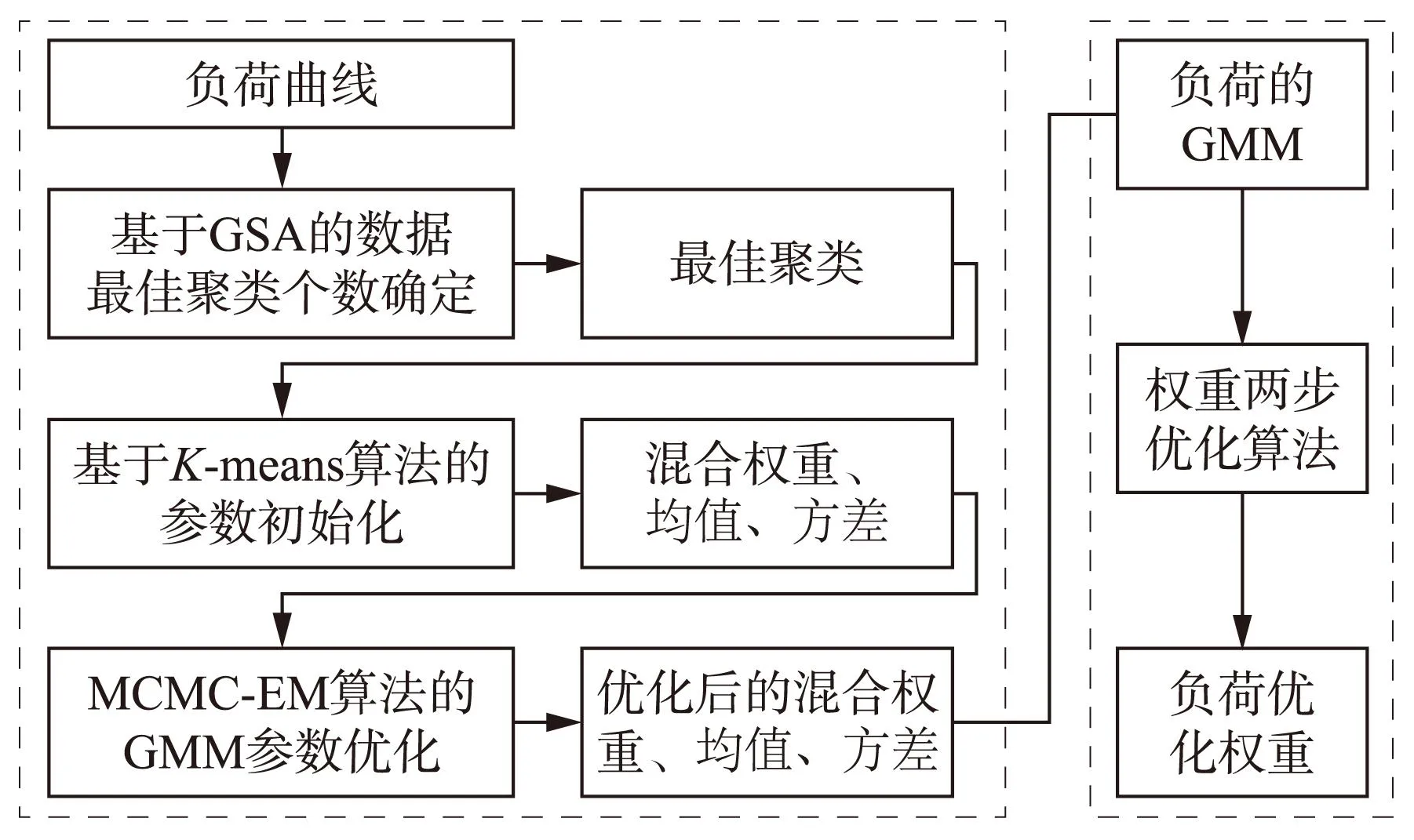
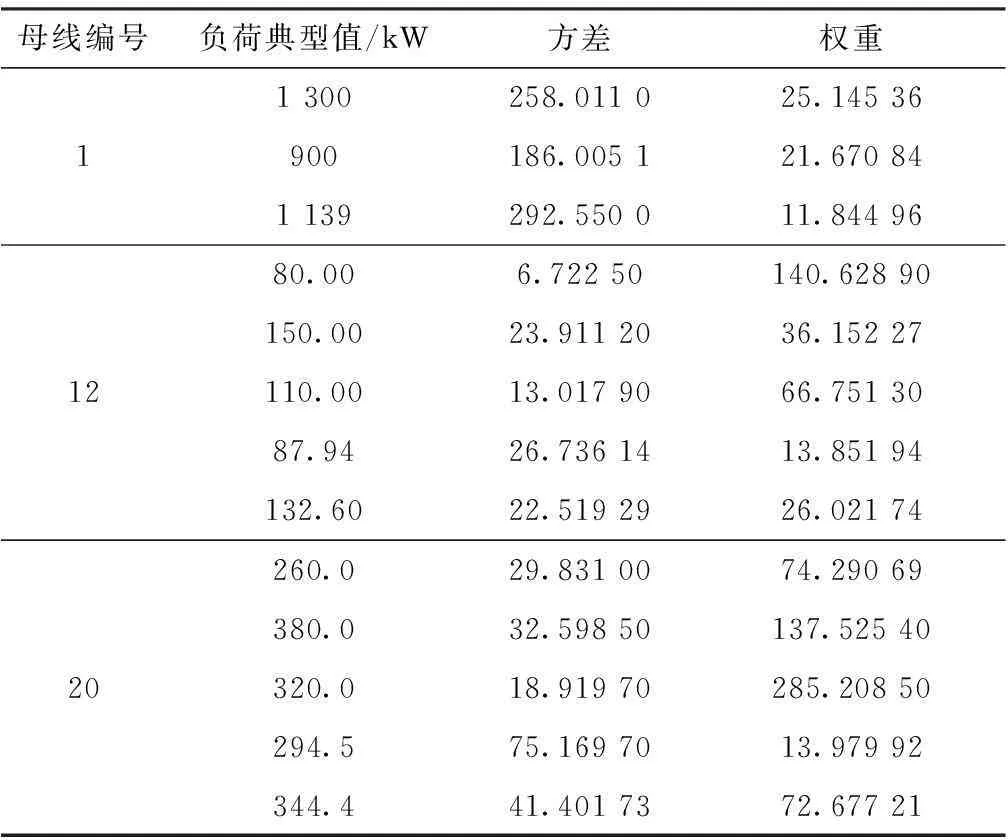
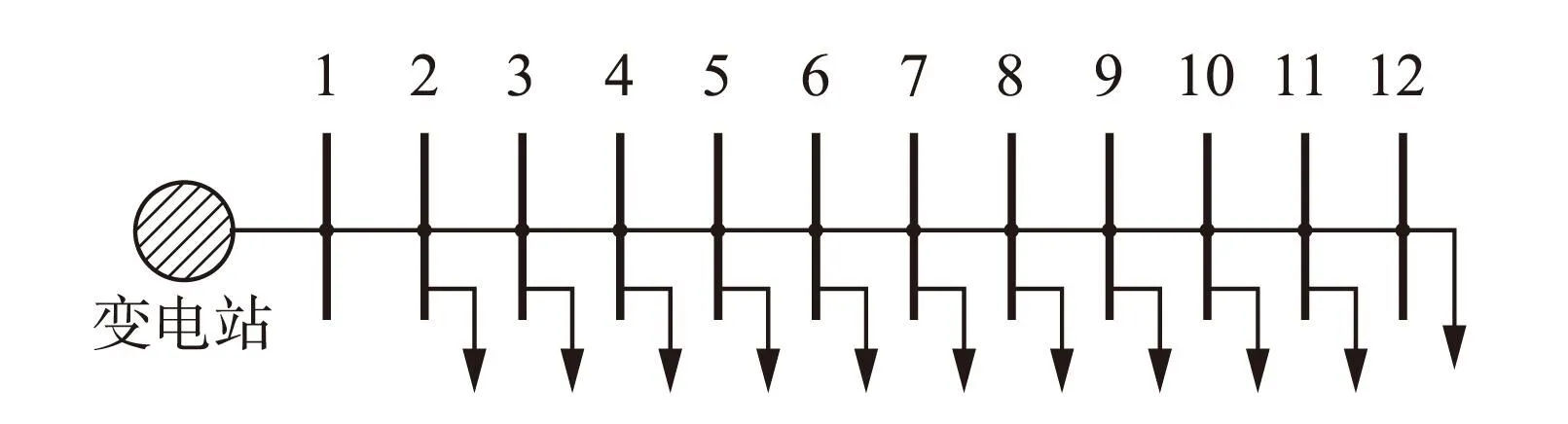
d) 将满足Dp,j

式中wm、um、Σm分别为优化成分权重、优化均值和优化方差。经过优化的负荷权重

为方便表述，准则一和准则二可总结为两步优化算法。通过前面分析，可以得出基于GMM的配电网负荷伪量测权重优化步骤，如图1所示。

图1　基于GMM的配电网负荷伪量测权重优化步骤

4算例分析

4.1权重优化

以某电网的若干条母线全年负荷为例，确定负荷量测的权重。每条母线的负荷数据以1 h为单位，全年共有8 760个数据点。图2给出了母线12的负荷概率密度分布估计结果，并对优化前后的GMM曲线作对比。

图2　母线12的负荷概率密度分布

从图2可以看出，优化后的GMM能够更好地拟合母线负荷观测值。表1给出了3条母线的GMM参数值。

表1不同母线的GMM参数

母线编号权重均值方差1(0.3295,0.6705)(1293.80,865.89)(258.0110,186.0051)12(0.2110,0.1796,0.6094)(79.72015,143.77030,106.35820)(6.7225,23.9112,13.0179)20(0.4285,0.3040,0.2667)(257.1195,382.2867,319.5181)(29.8310,32.5985,18.9197)

为了更好地说明所提GMM对负荷数据拟合的精确性，图3对几种常见分布类型的拟合结果进行了对比。

图3　母线12的不同分布拟合结果

从图3可以看出，相比于其他类型的分布，GMM对于负荷数据的拟合效果更好。表2给出了不同分布的拟合优度检验结果，可以更好地看出GMM的优越性。

根据负荷概率密度分布，选取母线负荷典型值。负荷典型值的选取原则是分别选取组合成分中均值附近的负荷值和组合叠加部分中间的负荷值。表3给出了不同母线在不同负荷值下的方差以及根据算法确定的权重。

表2　不同分布拟合优度检验

表3负荷典型值、方差和权重

母线编号负荷典型值/kW方差权重11300258.011025.14536900186.005121.670841139292.550011.844961280.006.72250140.62890150.0023.9112036.15227110.0013.0179066.7513087.9426.7361413.85194132.6022.5192926.0217420260.029.8310074.29069380.032.59850137.52540320.018.91970285.20850294.575.1697013.97992344.441.4017372.67721

由表3可以看出，GMM对不同母线在不同时刻确定的负荷伪量测权重都有一定程度的变化，比单一地将负荷伪量测权重设定为100(量测精度标幺值为0.3)更加合理。

4.2权重测试

本文基于支路电流的状态估计算法[13]，选取改进IEEE-12节点系统[14](如图4所示)，对经过优化的权重进行检验。选取实际运行负荷对母线负荷进行扩展，每条母线的负荷概率密度参数见表4。

图4　IEEE-12节点系统

状态估计的可靠性与估计值、真实值之间的偏差有直接的关系，偏差越小，可靠性越高，估计质量越好。以估计质量Qua衡量状态估计的质量，Qua越大，说明估计值与实际值偏差越小，估计质量越好。Qua的表达式为

其中

表4IEEE-12节点系统GMM参数

母线编号混合权重均值方差2(0.439,0.111,0.450)(25.8065,40.8720,59.4896)(2.6221,6.0284,7.1122)3(0.5211,0.2316,0.2473)(48.8898,62.4060,67.9136)(3.9552,3.6744,9.8798)4(0.8013,0.1987)(22.7843,49.8094)(9.0085,5.7466)5(0.3990,0.0474,0.5536)(68.4747,147.1932,158.9364)(21.7962,27.4489,35.7453)6(0.4333,0.4706,0.0961)(112.1427,53.8183,149.8037)(20.1555,25.8724,12.3098)7(0.5431,0.4390,0.0179)(43.1141,75.2489,114.2319)(11.4361,8.6408,11.2149)8(0.2690,0.5942,0.1368)(142.7637110.4933196.6833)(37.5280,24.8170,11.3136)9(0.2727,0.1703,0.5570)(66.4018,53.5852,82.9109)(4.0104,2.6423,6.4678)10(0.5431,0.4390)(43.1141,75.2489)(11.4361,8.6408)11(0.0685,0.2180,0.7134)(86.9408,41.4218,66.1209)(11.7523,3.7183,8.3164)12(0.8013,0.1987)(22.7843,49.8094)(9.0085,5.7466)

4.2.1不同实时量测误差下的权重测试

对实时量测添加不同的高斯噪声，比较不同实时量测误差下优化权重对状态估计的性能表现。算例1，实时量测误差1%，权重9×10-4；算例2，实时量测误差2%，权重2.25×10-4；算例3，实时量测误差3%，权重10-4。

图5对不同实时量测误差下权重优化前后的状态估计质量进行了对比。

图5　不同实时量测误差下的状态估计质量

从图5可以看出，在同一实时量测误差水平下，经过负荷伪量测权重优化后的估计质量高于优化前的估计质量，说明本文所提出的权重优化算法具有优越性；随着实时量测误差的增大，估计质量值减小，可靠性降低，说明实时量测的误差水平对配电网状态估计的可靠性起主导作用，而负荷伪量测的权重优化对状态估计的可靠性起改进作用。

4.2.2不同负荷伪量测误差水平的权重测试

对负荷伪量测添加不同的高斯噪声，比较不同负荷伪量测误差水平下优化权重对状态估计的性能表现。算例1，负荷伪量测误差10%，权重9×10-2；算例2，负荷伪量测误差20%，权重10-2；算例3，负荷伪量测误差30%，权重3.6×10-3。实时量测误差设定为1%。

图6对不同负荷伪量测误差下权重优化前后的状态估计质量进行了对比。

图6　不同伪量测误差下的状态估计质量

从图6可以看出：在同一伪量测误差水平下，经过权重优化的状态估计质量始终高于未经过优化的估计质量；随着负荷伪量测误差的增大，未经权重优化的状态估计质量值减小，而经过权重优化后的状态估计质量基本保持不变，说明人为统一设定负荷伪量测权重，不能准确地反映出当前的负荷伪量测误差水平，影响状态估计的可靠性，而通过负荷自身的GMM来确定负荷权重，是继承于负荷伪量测自身特征的数字量，能够很好地反映负荷的误差水平，提高状态估计质量，使估计结果具有较高的可靠性。

5结束语

本文提出了一种基于GMM的负荷伪量测权重优化方法。该方法首先通过组合算法(GSA、K-means算法和MCMC-EM算法的组合)对GMM的参数进行优化；然后通过权重优化两步准则确定某一母线的负荷方差，进而确定该负荷的量测权重。状态估计实例验证了本文提出的负荷伪量测权重优化方法的合理性和有效性，该方法最大程度地拟合了负荷自身的特性，但不适合特定时段的负荷特性。

本文提出的负荷权重确定方法能够很好地嵌入基于加权最小二乘法的配电网状态估计程序中。针对特定的电网母线负荷数据，首先建立母线负荷数据的GMM，然后预先计算和存储母线所覆盖的负荷量测权重，离线调用，也可根据本文提出的算法在线计算。

参考文献：

[1]FIKRIZ.StatisticalLoadAnalysisforDistributionNetworkPlanning[D].Sweden:RoyalInst.Technol.,Stockholm,1975.

[2]LIMAYEDR，WHITMOREC.SelectedStatisticalMethodsforAnalysisofLoadResearchData：EPRI-EA-3467[R].Bala-Cynwyd：UnitedStatesSynergicResourcesCorp.，1984.

[3]IRWINGW,MONTEITHW,BEATTIEWC.StatisticalElectricityDemandModellingfromConsumerBillingData[J].IEEEProceedingsC(Generation,TransmissionandDistribution),1986, 133(6): 328-335.

[4]SEPPALAA.StatisticalDistributionofCustomerLoadProfiles[C]//1995InternationalConferenceonEnergyManagementandPowerDelivery.[S.l.] :IEEE，1995: 696-701.

[5]HERMANR,KRITZINGERJJ.TheStatisticalDescriptionofGroupedDomesticElectricalLoadCurrents[J].ElectricPowerSystemsResearch, 1993, 27(1): 43-48.

[6]GHOSHAK,LUBKEMANDL,DOWNEYMJ,etal.DistributionCircuitStateEstimationUsingaProbabilisticApproach[J].IEEETransactionsonPowerSystems,1997, 12(1): 45-51.

[7]HEUNISSW,HERMANR.AProbabilisticModelforResidentialConsumerLoads[J].IEEETransactionsonPowerSystems, 2002, 17(3): 621-625.

[8] 李碧君，薛禹胜，顾锦汶，等. 状态估计中选取量测权值的新原则[J]. 电力系统自动化，2000(8)：10-14.

LIBijun,XUEYusheng,GUJinwen,etal.ANewCriterionofDeterminingMeasurementWeightsinPowerSystemStateEstimation[J].AutomationofElectricPowerSystems, 2000(8):10-14.

[9]REYNOLDSD.GaussianMixtureModels[J].EncyclopediaofBiometrics, 2008, 3(4):93-105.

[10]MOONTK.TheExpectation-maximizationAlgorithm[J].SignalProcessingMagazine,IEEE, 1996, 13(6): 47-60.

[11]TIBSHIRANIR,WALTHERG,HASTIET.EstimatingtheNumberofClustersinaDataSetviatheGapStatistic[J].JournaloftheRoyalStatisticalSociety:SeriesB(StatisticalMethodology), 2001, 63(2): 411-423.

[12]LEVINERA,CASELLAG.ImplementationsoftheMonteCarloEMAlgorithm[J].JournalofComputationalandGraphicalStatistics, 2001, 10(3): 422-439.

[13]WANGH,SCHULZNN.ARevisedBranchCurrent-basedDistributionSystemStateEstimationAlgorithmandMeterPlacementImpact[J].IEEETransactionsonPowerSystems,2004, 19(1): 207-213.

[14]DASD,NAGIHS,KOTHARIDP.NovelMethodforSolvingRadialDistributionNetworks[J].IEEEProceedings-Generation,TransmissionandDistribution, 1994, 141(4): 291-298.

Optimization Algorithm for Pseudo Measurement Weight of Power Distribution Network Load Based on Gaussian Mixture Model

SHEN Dinghui1, YU Xiaolei2, WU Dan3

(1. State Grid Anhui Electric Power Company Lu’an Power Supply Company, Lu’an, Anhui 237000, China; 2. State Grid Anhui Electric Power Company Zhongxing Electric Power Design Institute Co., Ltd., Hefei, Anhui 230000, China; 3. State Grid Jiangxi Electric Power Company Nanchang Power Supply Company，Nanchang, Jiangxi 330000, China)

Abstract：A kind of optimization algorithm for load measurement weight of power distribution network based on Gaussian mixture model (GMM) is presented which includes optimization and weight confirmation for GMM parameters. It firstly uses gravitational search algorithm (GSA) to judge optimal clusteringnumbers of data and K-means algorithm to obtain an initial clustering center, variance and mixed weight of data. Then it uses Markov chain Monte Carlo-expectation maximum (MCMC-EM) algorithm to estimate GMM parameters. Finally it presents the optimization method for pseudo measurement weight of load according to optimized GMM so as to confirm pseudo measurement weight of load. Improved IEEE-12 node system is taken for an example to verify the proposed method and the result indicates its reasonability and effectiveness.

Key words：power distribution network; state estimation; pseudo measurement weight; Gaussian mixture model (GMM); Markov chain Monte Carlo-expectation maximum (MCMC-EM)

收稿日期：2015-10-14

doi:10.3969/j.issn.1007-290X.2016.05.016

中图分类号：TM732

文献标志码：A

文章编号：1007-290X(2016)05-0086-06

作者简介：

申定辉(1989)，男，安徽六安人。助理工程师，工学硕士，主要从事电网状态估计、柔性交直流输配电、新能源并网等方面的研究工作。

于晓蕾(1989)，女，山东烟台人。工学硕士，主要从事柔性交直流输配电研究和电网规划设计工作。

吴丹(1985)，女，江西南昌人。高级工程师，工学学士，主要从事电网运行和规划设计工作。

(编辑李丽娟)