考虑风电置信水平的机组组合优化方法

王石，吴峰（河海大学能源与电气学院，江苏南京　211100）



考虑风电置信水平的机组组合优化方法

王石，吴峰
（河海大学能源与电气学院，江苏南京211100）

摘要：置信水平是将风电功率波动由概率形式体现的。随着节能减排的需求越来越大，考虑置信水平能够使系统机组不过多的安排机组备用，以免增加系统的运行成本。基于机组组合的方法，提出了一种考虑置信水平下的备用决策方法。通过考虑风电功率波动的概率分布和负荷波动的概率分布，建立联合概率密度函数，然后加入置信水平，得到不同置信水平下的系统基本发电成本和校正调度成本。采用IEEERTS算例，得出系统总成本。

关键词：置信水平；机组组合；概率分布；基本运行成本；校正调度成本

Project Supported by the National Natural Science Foundation of China（51422701）.

由于风电的间歇性和随机性，其输出功率随机波动[1]，电网必须维持足够的旋转备用保证电网的安全稳定运行。但由于正负旋转备用都具有一定的成本，过量的旋转备用总量会降低电网的经济性。因此，对备用总量的决策与优化是维持电网安全稳定运行、提高电网运行经济性的关键。

目前，针对旋转备用的决策与优化，相比于日内多级的有功调度[2]而言，日前机组组合方法的研究更为成熟[3-4]。为了应对风电的随机性和间歇性，常常过于频繁地调整机组出力，这对电网经济性带来巨大冲击。

为了防止不同时段机组调整出力过多，减少系统调度成本，本文通过考虑风力发电输出功率的置信水平[5-6]，将风电功率出力的不确定性以概率形式体现，研究在不同置信水平下，系统备用应对风电功率波动的分配与决策，以提高电网运行的经济性[7-8]。

文献[9]考虑风速波动与负荷波动的联合概率分布，确定备用决策与分配，但并没有考虑风速预测随时间越长越难以预测这一特点；文献[10]以发电成本与停电损失最小来决策出备用决策与安排，但没有考虑机组自身的爬坡约束；文献[11]通过对负荷波动、风电功率波动进行抽样统计，目标是为了使发电成本与停电损失最小，同样没有考虑机组爬坡约束和网络约束的影响。

本文考虑风电预测的置信度，采用风电功率区间预测，风电可能的波动区间随时间变长越来越大，同时，在考虑机组爬坡约束和网络安全约束的基础上，使得电网运行经济性达到最优。

1含风电系统不确定模型

电网运行时留有备用是为了应对系统中的不确定性，进而保持系统安全稳定运行。现在电网中的不确定性主要包括系统故障的不确定性，风电功率预测的不确定性和负荷预测的不确定性。本文着重研究后两者不确定性条件下，电力系统备用的安排和决策。

1.1风电功率概率模型

准确地预测风电功率，是保证含大规模风力发电电力系统安全、可靠和经济运行的关键。由经验可知，风速服从韦伯尔分布，但目前对风电功率并没有一个准确的模型。文献[12]得出风电功率服从正态分布，PW

为风电功率预测值，ΔPW为风电功率预

测误差，则实际风电功率PW=PW+ΔPW，实际风电功率概率分布函数为：

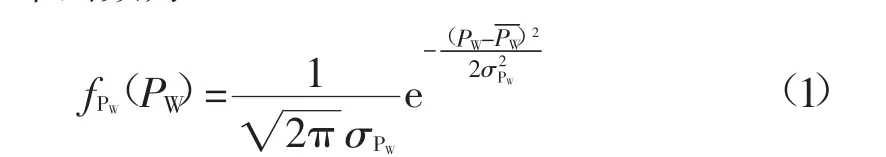
式中：PW为实际风电功率；σPW为风电功率的标准差。

1.2负荷预测误差概率模型

目前，负荷的预测已经比较准确，但还是存在一定的偏差，常采用正态分布来表示负合的预测误差[11]，ΔPL为负荷预测误差，其概率密度函数为：

式中：ΔPL为负荷预测误差；σL为负荷预测误差的标准差。

1.3风电功率和负荷的联合概率密度函数

本文综合考虑2种不确定性因素对电网运行的影响，设Z为系统功率偏差，即：

式中：PGΣ为所有常规机组出力之和。当Z＞0时，表示发电量过多，已经超过了系统需求，需要采取弃风的方式；当Z＜0时，表示发电量不足以满足系统需求，需要采用切负荷的方式。

由于风电预测功率和负荷预测误差之间相互独立，可对2部分的概率密度函数进行卷积，可得随机变量Z的概率密度函数为：

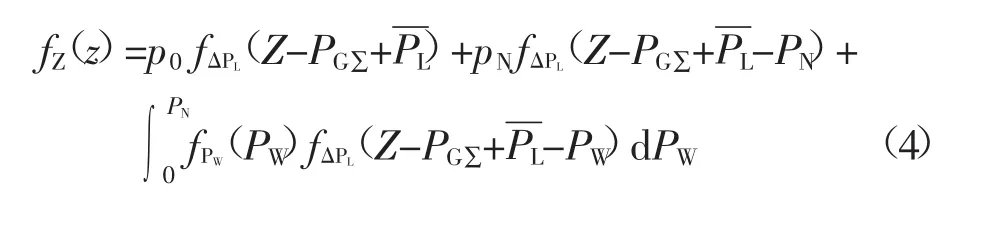
式中：p0为风电场输出功率为0时的概率；pN为风电场输出功率为额定功率PN时的概率；fPW（pW）为风电场输出功率为（0，PN）的概率密度函数。风电功率在（0，PN）之间波动，目前广泛采用变速恒频风机模型[12]，即：

式中：vin、vout和vN为切入、切出风速和额定风速。单纯风电功率点预测不能体现随时间变长越难以预测这一特点，通过采用区间预测的方式，不仅能直观地体现出时间特性，同时也能更好地表现出风电出力的概率形式。

2考虑风电功率置信水平的数学变换

2.1风电功率预测区间下的数学模型

伴随时间尺度的变大，风电功率预测区间也会变大，功率率波动PW在［PW分别为风电功率预测区间上、下限。由此，原先由点预测产生的随机变量Z的概率密度函数变为：，PW］之间，PW、PW

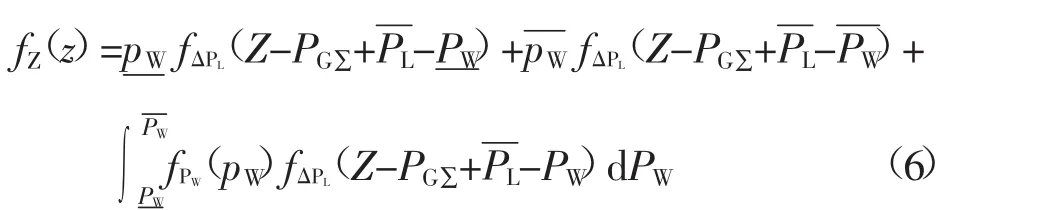
式中：pW为风电功率取PW为风电功率取时的概率；pWPW时的概率。由概率论[13-15]可知，在连续取值范围内，某一点取值的概率为0。则式（6）可变换成：

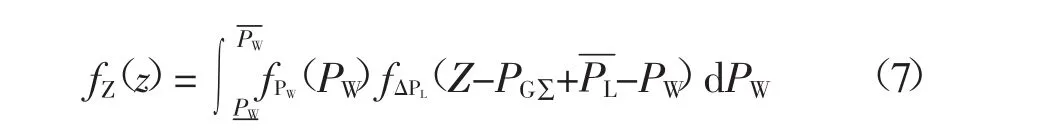
2.2考虑风电功率置信水平的数学模型变换

风电场不光提供风电功率基准值和风电功率预测区间，一般还会提供风电功率的概率密度函数，本文采用正态分布函数进行模拟。根据概率密度函数，取不同的风电置信水平要求，可以得到不同的风电功率允许区间。

假设已知风电功率的概率密度函数，根据文献[16]可知，通过基于Nataf变换的蒙特卡洛法可得到风电功率的累计概率函数。由此可得到风电功率的允许区间上下限：

式中：β为置信水平，ξt为风电功率在置信水平β下允许区间的边界值。由此，可得出24时段的风电功率预测区间，根据式（7），可将原式改成：

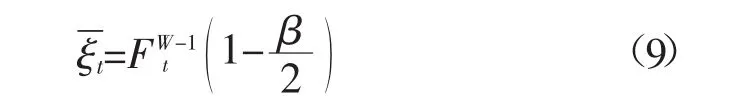
、ξt

3考虑风电置信水平下系统备用决策与安排

当正旋转备用全部投入时，功率仍有缺额，即Z+RU＜0时，需要切负荷，可得出失负荷期望为：

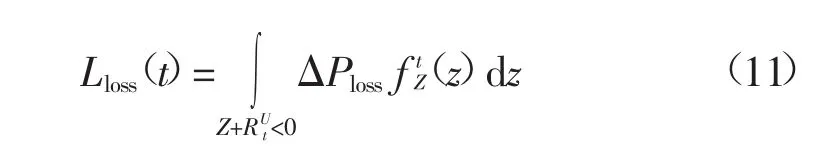
式中：ΔPloss=－（Z+RUt）；

当负旋转备用全部投入时，功率仍有富余，即Z－RD＞0时，需要弃风，可得出弃风期望为：

式中：ΔWloss=Z－RDt。

3.1备用决策

由于正旋转备用与失负荷相关，负旋转备用与弃风相关，而正负旋转备用、失负荷与弃风都存在一定的经济成本，可建立2个以正、负旋转备用为变量的函数：

式中：cU正负旋转备用成本；cL为失负荷成本；cW为弃风成本。将式（11）和式（12）代入式（13），可得：R、cDR为

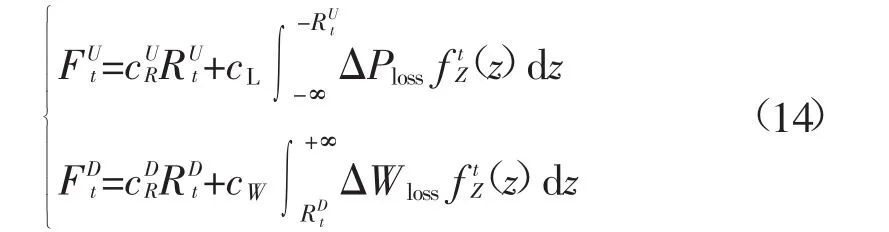
基于式（11）进行优化，即可得到经济最优时对应的总正负旋转备用RUt、RDt。

3.2备用分配

采用优先顺序法[17-18]确定机组启停状态，优先顺序法的指标为机组的满负荷平均煤耗率：

式中：ai、bi和ci为机组i的发电成本系数。根据满负荷平均煤耗率对机组进行排序，依次从大到小加入机组，且在各时段满足机组出力约束、机组爬坡约束、机组最小启停约束和网络安全约束，通过采用二分法的经济调度方式分配机组出力，流程图如图1所示。

4考虑风电置信水平下系统总成本

在电力系统运行中，成本分为基本运行成本和调度成本。基本运行成本S0指的就是发电机组出力成本之和，其中：

而校正调度成本SJ为重新调整机组出力成本、释放备用容量成本、再弃风和再切负荷成本成本，其中：

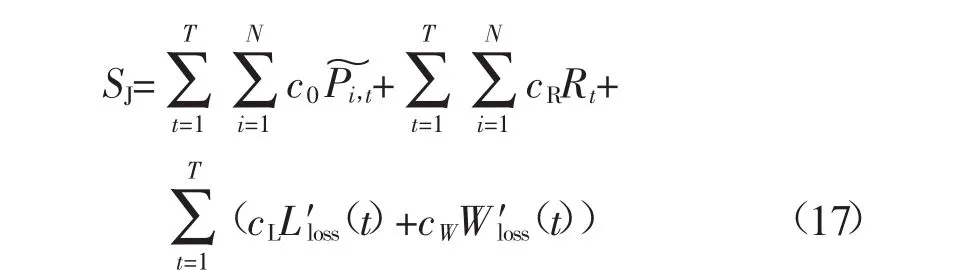
式中：c0为重新调整单位机组出力成本；～Pi，t为 第i机组第t时刻的出力变化量；cR为释放单位备用容量成本；Rt为第t时刻释放备用容量总和；L′los（st）和W′los（st）为第t时刻再切负荷与再弃风期望。

由本文目的可知，目标函数为：

式中：S为系统总成本，根据改变β的取值，找到系统最小总成本与此时对应β的取值。

5算例分析

本文中采用IEEE24节点系统负荷与风电预测区间数据，如图2所示，该风电场接在9号节点。由于各时段预测区间占u±3δ区间的99.7%[16]，由此可得到风电风电功率的累计函数。取置信水平β=0.5，

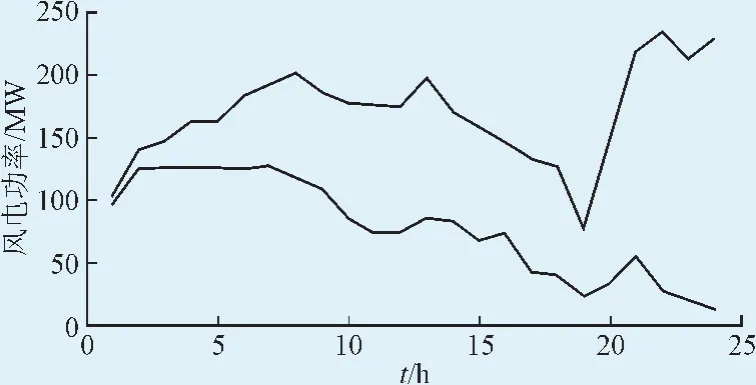
图2风电功率预测区间Fig. 2 Prediction interval of wind power

再根据式（25）和式（26），可得到此时风电功率的允许区间，如图3所示。由于当前对风电功率的概率密度函数没有一个确定的模型，本文主要考虑备用的决策与分配，取正旋转备用成本为20 $/（MW·h），失负荷成本为1 000 $/（MW·h），负旋转备用成本为11 $/（MW·h），弃风成本为50 $/（MW·h），再根据式（11）可得出风电预测区间下的正旋转备用与切负荷成本、负旋转备用与弃风成本。根据计算可得，随着正旋转备用的逐渐增加，失负荷期望逐渐减小，失负荷和正旋转备用成本先减小后增大，且随着负旋转备用的逐渐增加，弃风期望逐渐减小，弃风和负旋转备用成本先减小后增大。由此可得到各个时段的正负旋转备用总量，根据二分调度发对备用进行分配，且满足各约束条件。同理，求出允许区间下的备用决策与分配。由图4、图5可知，不同置信水平决策出的备用总量不一样，随着置信水平的增加，所需备用容量在减少，同时意味着调度中所需释放的备用容量在增加。

通过采用蒙特卡罗法，抽取1 000组在预测区间内、服从正态分布的风电功率出力曲线，算出各组数据下的调度成本，最后取均值，可得到校正调度成本。设重新调整机组出力成本为80 $/（MW·h），备用释放成本为50 $/（MW·h），切负荷成本为1 000 $/（MW·h）。对于不同的置信水平，可得到不同的调度成本，如图6所示。随着置信水平的增加，系统校正调度成本在逐渐增加。

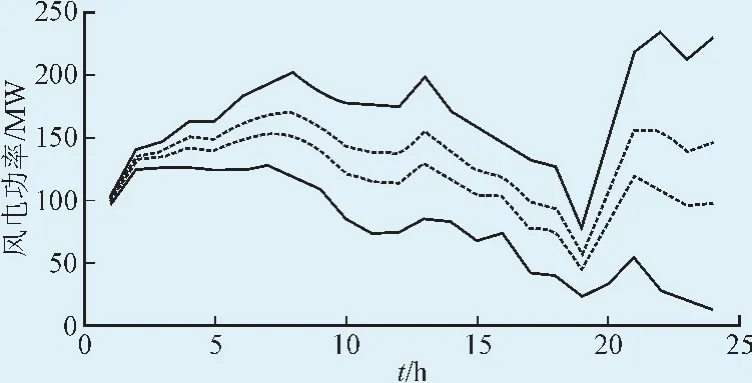
图3风电功率预测区间与允许区间Fig. 3 Prediction interval and allowable interval of wind power

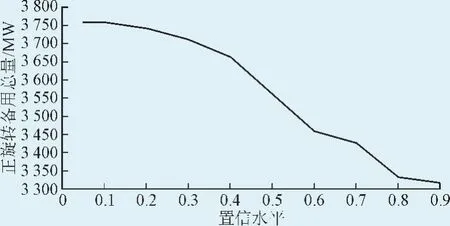
图4不同置信水平下的正旋转备用总量Fig. 4 Up spinning reserve amount in different confidence levels

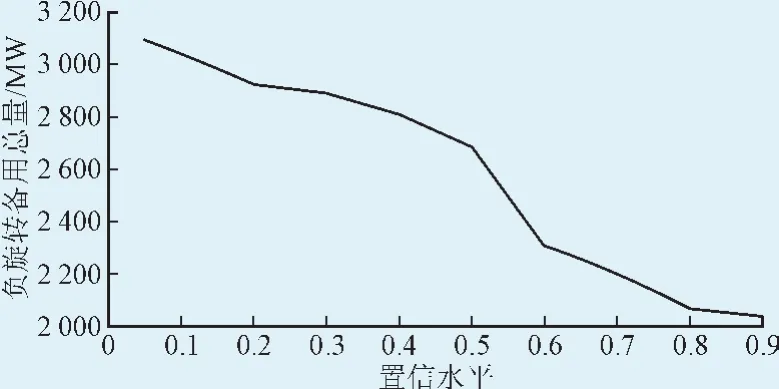
图5不同置信水平下的负旋转备用总量Fig. 5 Down spinning reserve amount in different confidence levels

图6校正调度成本Fig. 6 Calibration schedule cost

而系统基本运行成本在不断减小。由此可知，系统总成本如图8所示，在置信水平为0.6时达到经济最优。

图7基本运行成本Fig. 7 Basic operating cost

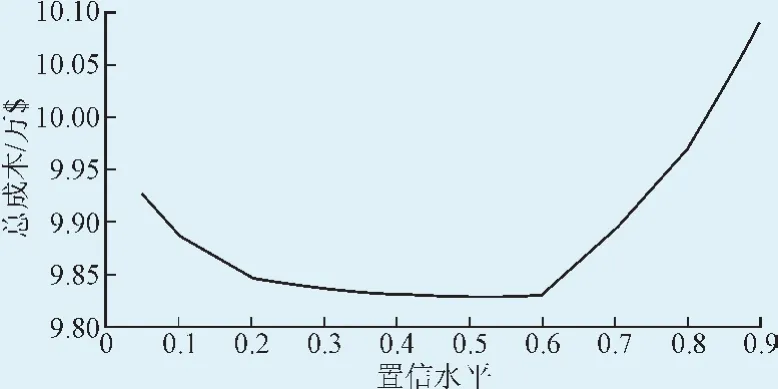
图8系统总成本Fig. 8 The system’s total cost

6　结语

本文针对风电功率的预测方式不同，由原先的点预测变成区间预测，可展现出风电功率随时间的增加，越来越难以预测的特点。加入置信水平之后，可通过改变风电功率区间，使波动变小。通过比较预测区间下和加入置信水平允许区间下的机组出力与备用决策和安排，可以看出，随着置信水平的增加，风电功率波动越来越小，但所需要付出的校正调度成本也在逐渐增加。由此可知，加入置信水平后，可以权衡系统基本运行成本和校正调度成本，使系统达到经济最优。

参考文献

[1] GU Yingzhong，XIE Le．Look-ahead dispatch with forecast uncertainty and infeasibility managemen[C]// IEEE Power Engineering Society General Meeting，July 22-26，2012，San Diego，USA：7p．

[2]张国强，吴文传，张伯明．考虑风电接入的有功备用协调优化[J].电力系统自动化，2012，40（13）: 110-114. ZHANG Guoqiang，WU Wenchuan，ZHANG Boming．Optimization of operation reserve coordination considering wind power integration[J]．Automation of Electric Power Systems，2012，40（13）：110-114（in Chinese）．

[3]陈皓勇，王锡凡．机组组合问题的优化方法综述[J]．电力系统自动化，1991，23（5）：51-56. CHEN Haoyong，WANG Xifan．A survey of optimizationbased methods for unit commitment[J]．Automation of Electric Power Systems，1991，23（5）：51-56（in Chinese）．

[4]杨朋朋．机组组合理论与算法研究[D]．济南：山东大学，2008．

[5]崔晓丹，李威，任先成，等．大规模风电接入的输电网规划研究评述[J]．江苏电机工程，2012，31（6）：1-6．CUI Xiaodan，LI Wei，REN Xiancheng，et al．Review of the research on transmission network planning with large scale wind power connected[J]．Jiangsu Electrical Engineering，2012，31（6）：1-6．

[6]朱雨彤，靳晶.多时间尺度相协调的电力市场价值评估[J].江苏电机工程，2015，34（5）：47-50．ZHU Yutong，JIN Jing．Evaluation on the value of multiple time-scale electricity market[J]．Jiangsu Electrical Engineering，2015，34（5）：47-50（in Chinese）．

[7]李智，张新松，郭晓丽．大规模风电接入火电系统的最优旋转备用容量研究[J]．电力系统保护与控制，2012 （13）：110-114．LI Zhi，ZHANG Xinsong，GUO Xiaoli．Study on the optimal spinning reserve in thermal power system with significant wind power penetration[J]. Power System Protection and Control，2012，40（13）：110-114（in Chinese）．

[8]张新松，袁越，傅质馨．基于隐性备用约束的机组组合模型[J]．电力系统保护与控制，2013（1）：136-142．ZHANG Xinsong，YUAN Yue，FU Zhixin．The unit commitment formulation with implicit reserve constraint[J]. Power System Protection and Control，2013，41（1）：136-142（in Chinese）．

[9]赵晋泉，唐洁，罗卫华，等．一种含风电电力系统的日前发电计划和旋转备用决策模型[J]．电力自动化设备，2014（5）：21-27．ZHAO Jinquan，TANG Jie，LUO Weihua，et al．Dayahead generation scheduling and spinning reserve decisionmaking model for power grid containing wind power[J]．Electric Power Automation Equipment，2014，34（5）：21-27（in Chinese）．

[10]李志刚，吴文传，张伯明．消纳大规模风电的鲁棒区间经济调度（一）调度模式与数学模型[J]．电力系统自动化，2014（20）：33－39．LI Zhigang，WU Wenchuan，ZHANG Boming．A robust interval economic dispatch method accommodating largescale wind power generation：Part one dispatch scheme and mathematical model[J]．Automation of Electric Power Systems，2014，38（20）：33-39（in Chinese）．

[11]李志刚，吴文传，张伯明．消纳大规模风电的鲁棒区间经济调度（二）不确定集合构建与保守度调节[J]．电力系统自动化，2014（21）：32－38．LI Zhigang，WU Wenchuan，ZHANG Boming．A robust interval economic dispatch method accommodating largescale wind power generation：Part two uncertainty set modeling and conservativeness adjustment[J]．Automation of Electric Power Systems，2014，38（21）：32-38（in Chinese）．

[12]范高峰，王伟胜，刘纯，等．基于人工神经网络的风电功率预测[J]．中国电机工程学报，2008，28（34）：118-123．FAN Gaofeng，WANG Weisheng，LIU Chun，et al．Wind power perdiction based on artificial neural network[J]．Proceedings of the CSEE，2008，28（34）：118-123（in Chinese）．

[13] JUAN M M，JUAN P R．Point estimate schemes to solve the probabilistic power flow[J]．IEEE Transactions on Power Systems，2007，22（4）：1594-1601．

[14] ZHAO W，CHEN Z，Blaabjerg F．Probabilistic capacity of a grid connected wind farm based on optimization method[J]．Renewable Energy，2006，31（13）：2171-2187．

[15]盛骤，谢式千，潘程毅．概率论与数理统计[M].北京:高等教育出版社，2004.

[16] CHEN Y，WEN J，CHENG S．Probabilistic load flow method based on Nataf transformation and Latin hypercube sampling[J]．IEEE Trans on Sustainable Energy，2013，4 （2）：294-301.

[17]黎静华．适合于机组组合问题的扩展优先顺序法[J]．电力系统保护与控制，2010，38（2）：1-7．LI Jinghua．Extended priority list method for unit commitment problem[J]．Power System Protection and Control[J]. 2010，38（2）：1-7（in Chinese）．

[18] PUKELSHEIM F．The three sigma rule[J]．The American Statistician，1994，48（2）：88-91．

王石（1991—），男，硕士研究生，研究方向为新能源接入备用容量优化；

吴峰（1977—），男，博士，教授，博士生导师，研究方向为可再生能源发电系统的建模与控制。

（编辑董小兵）

Optimization Methods of Unit Commitment Using a Confidence Levels’Method

WANG Shi，WU Feng
（College of Energy & Electrical Engineering，Hohai University，Nanjing 211100，Jiangsu，China）

ABSTRACT：Confidence levels reflect wind power volatility in the way of probability. With the growth of demand of energy conservation and emissions reduction，it is useful for avoiding too much unit reserve to consider confidence levels，so that it can avoid increasing the cost of system operation. This paper is based on unit commitment to come up with a way of considering confidence levels’reserve determination. Considering the probability distributions of the wind power volatility and the load volatility，it can establish the function of joint probability density，and add the confidence levels to the function，so as to calculate the system basic operation cost and calibration schedule cost in different confidence levels. IEEE-RTS is taken as the example to demonstrate the efficiency of the method proposed in this paper.

KEY WORDS：confidence levels；unit commitment；probability distribution；basic operating cost；calibration schedule cost

作者简介：

收稿日期：2015-10-17。

基金项目：国家自然科学基金项目（51422701）。

文章编号：1674- 3814（2016）02- 0116- 06

中图分类号：TM614

文献标志码：A