引信可靠性考核的系统性错误及统计检验方法

张龙山

(机电动态控制重点实验室，陕西 西安 710065)



引信可靠性考核的系统性错误及统计检验方法

张龙山

(机电动态控制重点实验室，陕西 西安 710065)

摘要:针对引信可靠性考核中可靠度单侧置信下限表仍在起决定性作用的乱象，再次证明查该表判断引信可靠性是否达标，或由该表确定抽样方案均为系统性错误，错在该表的“置信度”是拒止置信度，这样做没有法理依据。提出执行GJBz 20119时，将“可靠度-置信度”指标理解为“可靠性-通过置信度”。考核可靠性时，依据GJB 179A制定方案进行抽样检验，或依据GB/T 4088-2008进行假设检验；可靠度单侧置信下限表仅仅用作区间估计或查拒止指标。DRP系列等一些产品和文中实例表明，这样做是可行、可操作的。

关键词:引信；可靠性；置信水平；假设检验

0引言

可靠性要求达到0.93以上，置信度0.9，我们的方案是(54,1)；同样的要求，美军制定的抽样方案是(16,2)。如此简单的问题怎么会有如此悬殊的答案？文献[1]指出，是我们错了。

“不低于0.93则通过”与“低于0.93则拒止”，对于全数检验是同义语；但是对于抽样检验是完全不同的两个概念。抽样结果有随机散布，只要实际成功率不为0或100%，抽样中通过或拒止的可能性都存在。在高概率通过与高概率拒止之间有一个灰色中间地带，通过与拒止的概率都不太低，不确定。没有人喜欢灰色地带，但它是令人无奈的客观存在。灰色地带可以通过增加样本量压缩，但是直到产品全部抽完才能消灭。量变到质变，此时已经变成全数检验。

文献[1]指出我们的错误在于张冠李戴，以高概率拒止指标充当作高概率通过指标。采用方案(54,1)时，已知可靠性0.93的产品被拒止的概率是0.9——我们在认真、负责、广泛、持久地干着如此荒唐的事情。但是文献[1]也存在不足，有些道理没有讲透，策略有偏差，可操作性不够。因此发表两年来没有起到多大效果。为了实实在在地解决这一困扰引信界的痼疾，以免贻笑后人，特撰此文，换个角度证明我们的可靠性考核方法确实存在系统性错误，指出错误原因并提出纠正办法。

1相关文献概要

1.1《以成功率表述引信可靠性指标》[1]

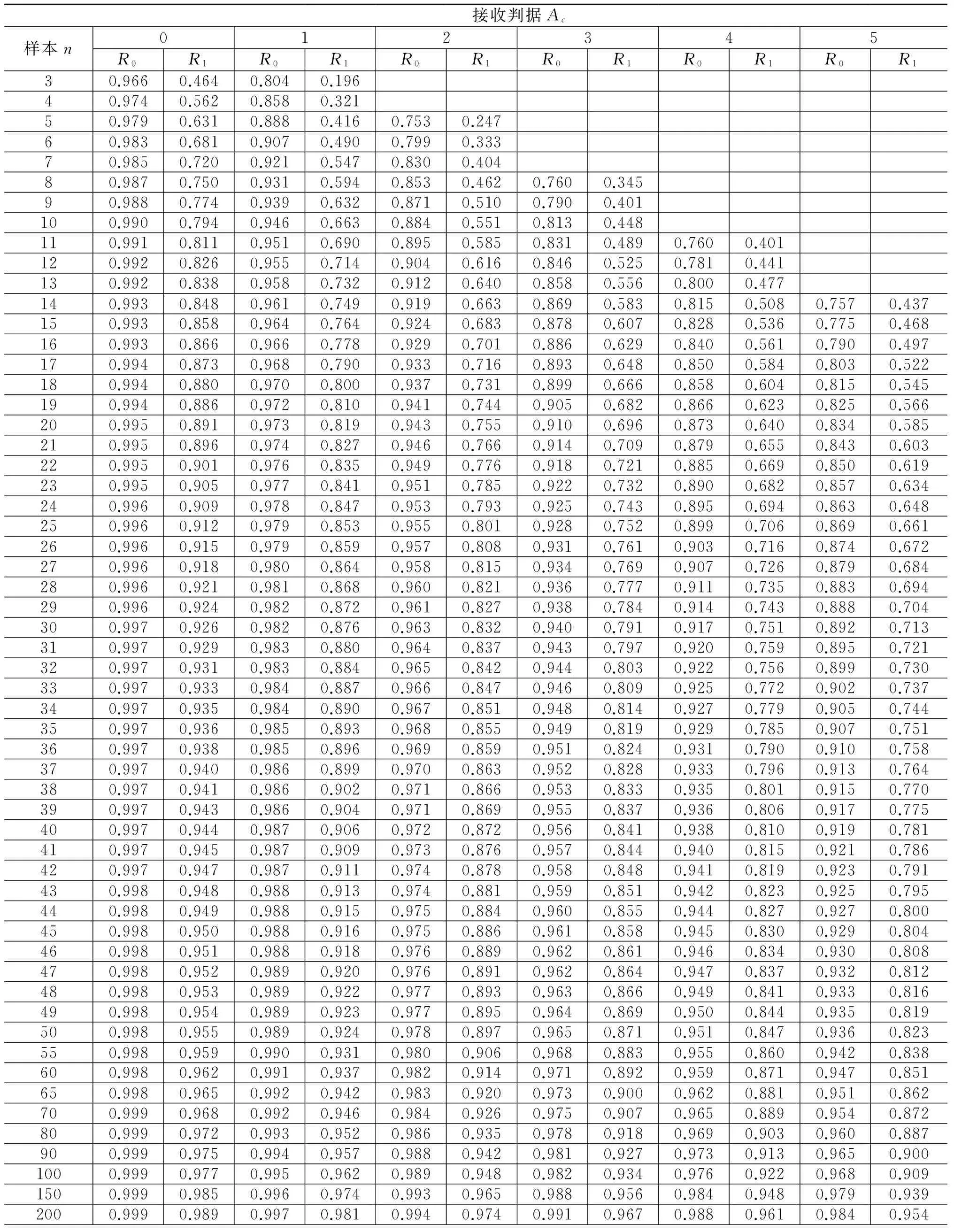
介绍了抽样检验基础知识，给出了有关概念的关系图，见图1。该图直观地示出失效率-接收概率、成功率-拒止概率两个坐标系以及其上参数的互补关系。

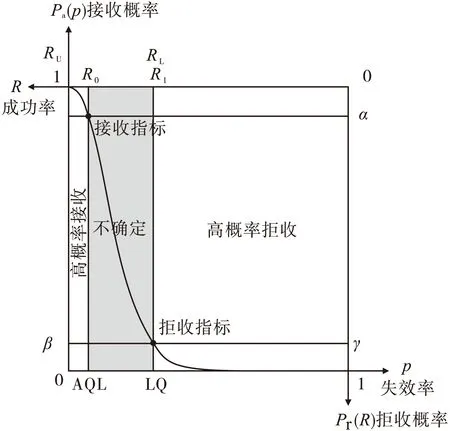
图1　抽样检验指标与可靠度性相关概念Fig.1　Sample index and reliability concept

文献[1]指出由可靠度单侧置信下限表查出的“可靠度”并不是常人心目中的可靠度下限，而只是抽样结果表现出的可靠性的可能区间，区间上限为1，下限值等于“拒止成功率”R1；其“置信度0.9”是拒止概率。当错以R1作为可靠性指标时，造成产品可靠性低下的假象，更可怕的是，无意中将真正的可靠度下限——“可接收的成功率”R0抬到了0.99附近，甚至更高。但是文献[1]也存在不足：

1) 把其中表1的GJB 450A[3]的“可靠性设计参数”说成“可靠性指标”，不确切。其实“可靠性评估”本身就是可靠性可能区间的估计方法，其“参数”是方法的指标，而不是产品的指标。

2) 尽管也说到抽样检验的指标不是产品的指标，是抽样方案的指标，但是只说到产品可靠性指标 “可以”用成功率或故障率，份量不够。不是可以，而是只能。

3) 指出了“置信水平”γ(=1-β)是拒止概率，但没有说出通过概率1-α是什么，不利于进一步认识错从何来。

4) 结论和摘要中都要求停用“可靠度”指标，给人以非修订标准无法纠正的印象，不够策略。

5) 提出的变通策略是保持可靠度-置信度指标不变，增添可接收成功率指标，但是论证的结果又是样本量过大，行不通。没有提供可操作的变通方法。

1.2GB/T 4088-2008《数据的统计处理和解释 二项分布参数的估计与检验》[4]

规定了由抽样结果对总体故障率参数作点估计、区间估计和假设检验的方法及示例。

给出了二项分布样本n抽到x个故障的概率计算式：

(1)

式中，n为样本量，x为故障数，p为故障率。

二项分布参数的检验中，给出了上限单侧检验方法。上限单侧检验拒绝域临界值c2的计算式：

(2)

式中α为显著性水平，1-α为置信水平，p0为故障率表达的可靠性指标。满足此式c2的最小整数为“单侧检验拒绝域上限”。为方便操作，该标准给出此式算出的E.1表。对于α=0.1，由样本为n=2～50，故障率0.01、0.02、0.03、0.05、0.10、…可查到相应c2。

该标准附录还介绍了假设检验的两种等效方法。其中的“置信区间法”的近似计算公式误差较大，式中参数要查χ2表，较麻烦，而且“上限”、“下限”很容易张冠李戴，这里仅摘录接收概率法。

原假设H0：p≤p0(即不合格率低于指标)，计算：

(3)

P>α，则不拒绝H0假设。

1.3GJBz 20119-93《炮兵引信战术技术指标通用要求》[5]

规定了对目标作用率以0.9置信度下的可靠度表述。

1.4GJB 376-87《火工品可靠性评估方法》[6]

主要内容为计量检验，也有计数检验。介绍了区间估计，定义了“计数数据估计可靠度”为“利用计数数据估计总体合格率的单侧置信下限”RL，置信水平为γ。给出了用用二项分布估计可靠度单侧置信下限RL的计算公式(4)，和超几何分布估计可靠度单侧置信下限的计算式(5)，以及用式(5)算出的可靠度单侧置信下限表。

(4)

=1-γ

(5)

式中N为总量，n为样本量，F为样本不合格数。

该标准部分术语与现行标准不同，例如将“参数估计”称为“数据估计”。特别是文中多处“可靠度”不是通用标准和常人心目中的“可靠性的概率度量”[2]，而仅仅作为“可靠度单侧置信下限”RL的缩略词，极易混淆。

但是其“可靠度”定义前面有定语“计数数据估计”，概念和用途明白无误。特别值得注意的是其示例，发火可靠度指标R≥0.999，批量N为 1 500，样本n为 416，不合格数F为0。查表得到可靠度单侧置信下限0.993 9。明明0.993 9低于指标0.999，但结论却是“满足可靠性指标”！没有错，该表的作用就是区间估计，估计结果并非产品可靠性为0.993 9，而是产品可靠性在0.993 9～1区间，0.999在此区间之内，无理由认为(416,0)不满足指标。

1.5GJB 179A-96《计数抽样检验程序及表》[7]

等效参照美军标MIL-STD-105E。规定了由批量、用途和可靠性检验指标AQL选方案和抽样方法。该标准也存在术语有异于现行标准的问题，但数表内容与新版国标和国际标准没有区别。

1.6美军可靠性指南[8]

该指南指出对于一次性产品的可靠性考核应当采用以故障率论可靠性的MIL-STD-105，或以成功率论可靠性的BS6001。

2可靠性考核的系统性错误

2.1错误所在

文献[1]已经指出我们的流行做法是错的。但是如果数理统计基础不足，一下子记不住那么多符号、概念，不容易看懂，至少是印象不深。本文换个角度再证明一次。

首先统一思想，“置信度0.9-可靠度0.93”的涵义到底是什么。大多数同志会回答：有90%的把握保证产品可靠性不低于0.93。但是文献[1]已证明，为了做到这一点，已知可靠性0.93的产品通过的概率只有0.1。(54,1)方案对于可靠性达到0.97的产品拒止概率都高达0.49。这显然不是我们的初衷，怎能容许如此败家？如果换个角度提问，对于已知可靠性0.93的产品，应当是“通过的概率为0.9”，还是“拒止的概率为0.9”？大多数同志会回答是通过的概率。对，美国人就是按此答案操作的。下面以方案(54,1)为例作核对。

当按样本n=54，已知可靠性0.93的产品抽到故障数为0、1、2、…的概率可以用(1)式计算，(1)式来自最浅显的组合统计，见之于所有数理统计教科书和手册，正确性毋庸置疑。

可靠性0.93换算为故障率p=0.07。分别算出抽到0、1、2、…9个故障的概率，列于表1。

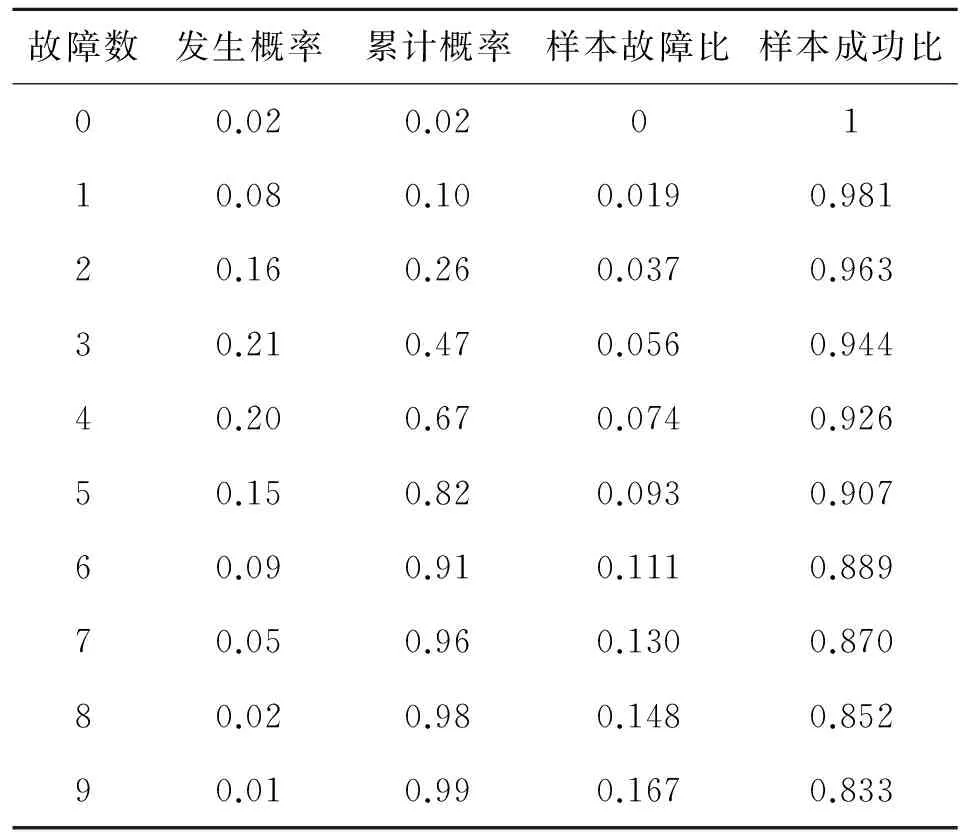
表1　可靠性0.93的产品样本54的故障数分布

图2的柱状图形象地画出了表1的第1、2列。故障数为0时，已知可靠性0.93的产品通过概率只有0.02；如果允许有0和1个故障，通过概率为0.02+0.08=0.1(表1第3列的累计概率)。

图2　置信度0.9，R0=0.93，(54,1)方案Fig.2　Confidence 0.9, R0=0.93,(54,1) scheme

结论出来了，本以为可靠性0.93的产品的通过概率是0.9，谁知算出通过概率只有0.1(拒止概率才是0.9)。与我们朴素的愿望正好相反，再次证实了文献[1]的说法，我们错了。

继续累加下去，允许有0、1、2个故障，通过概率为0.26……要到允许0～6个故障，通过概率才能达到0.9，得出的方案是(54,6)，见表1。即通过界限应当画在6，通过概率才能达到0.9，见图3。

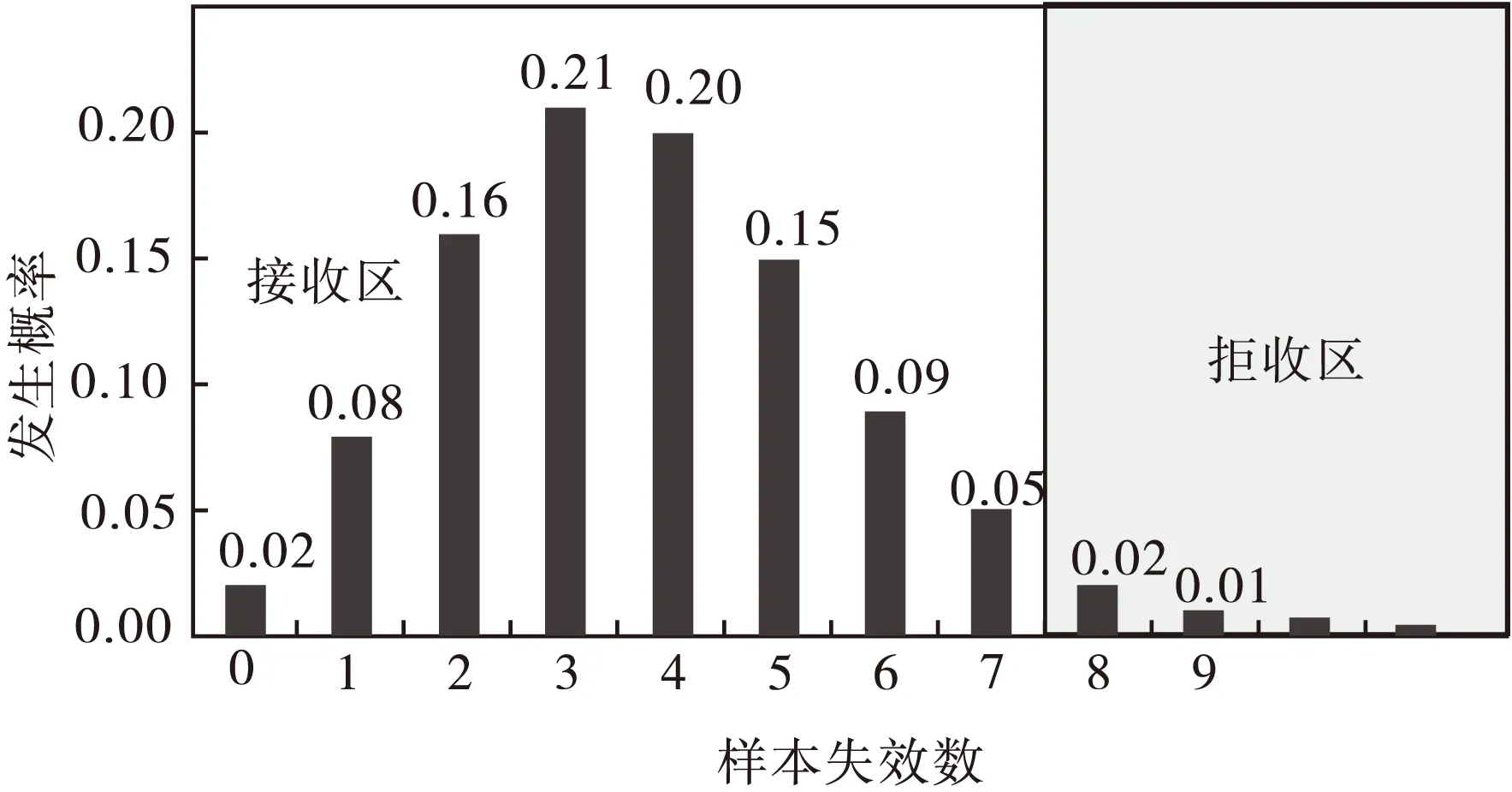
图3　置信度0.9，R0=0.93，(54,6)方案Fig.3　Confidence 0.9, R0=0.93,(54,6) scheme

2.2错从何来

一次性产品各种指标中，只有成功率(或故障率)是产品的可靠性指标。只要引入置信水平之类的概率概念，就一定涉及了抽样，变成了抽样检验的指标。而抽样检验的指标向来是成双成对的，有通过指标和拒止指标。

法院判案首先要指明适用法律、适用条款，考核可靠性一定要区分场合、选用适用标准。抽样作可靠性评估只在没有指标时才用。可靠性评估只适用于对可靠性一无所知的产品作粗略估计，对于从立项就有军代表跟踪、超过使用期出问题仍可追究的产品，并不适用。如果硬将抽样检验指标当作产品指标用，则如文献[1]所证明，在1-β和γ均被规定为0.9时，区间估计单侧置信下限RL与拒止指标R1相同。我们的错误正是将拒止指标当作通过指标使用。

最早把“置信度-可靠度”这一概率概念引入引信行业的是GJBz 20119[5]，但是该标准没有提及可靠度的涵义，起草者和执行者对“可靠度”的理解实际上是全数检验的“成功率下限”。而且，该标准也没有提及可靠度考核方法。

有计数抽样可靠度评估方法，并使用可靠度单侧置信下限表的国军标是GJB 376[6]，但是该标准中“可靠度”并非GJB 451A[2]及常人心目中的广义可靠度，而仅仅是区间估计中狭义的“单侧置信下限”，并且该标准只字未提查表可以选抽样方案。特别是该标准的示例，对于现行用法认为不达标的结果，下了达标的结论，从反面证明了现行用法是错的。

两个被认为是源头的标准实际上都不支持现行用法，可见查可靠度单侧置信下限表求产品可靠度，或以此选方案的现行用法没有法理依据，只是以讹传讹的错误习惯。

2.3认识置信水平，正确使用单侧置信下限表

文献[1]提出停用“可靠度”指标，容易被理解为必须修订标准，较难实现。不妨换一种思维，变通。可以按照大家“成功率0.93的产品的通过概率为0.9”的朴素概念解读可靠度-置信水平。

由文献[1]可知，错误在于不了解只要涉及抽样就有两对指标，不了解拒止指标不能单独使用，不了解“可靠度单侧置信下限”当作指标使用时是拒止指标，而将拒止指标当作通过指标使用。具体操作中，错在查了可靠度单侧置信下限表。

由文献[4]可知，1-α也是置信水平。原来，只要抽样，不仅指标有两种，“置信水平”也有两种，文献[1]介绍的置信水平γ(=1-β)只是“拒止置信水平”；此外还有“通过置信水平”1-α。而我们要查的恰恰是能通过的置信水平。

这样，执行GJBz 20119的变通方法就出来了：只要我们将“置信度”解读为“通过置信水平”(1-α)，将“可靠度”解读为“可接收成功率”(R0=1-AQL)，可靠度-置信度就变成了抽样检验的接收指标，从而与国际接轨，可以使用GJB 179A等标准，可以得出与美军相同的抽样方案。

但是可靠度单侧置信下限表只有拒止置信水平γ，没有通过置信水平(1-α)，张冠李戴，一查就错。本来只要概念清楚，知道通过置信水平0.9与拒止置信水平0.1的互补关系，数表是可以互相转换借用的。因此可靠度单侧置信下限表如果能查“置信水平”γ=0.1，也是可以的。但是可靠度单侧置信下限表的γ值只有0.50～0.99，查不到0.1，所以不能借用。

应该查什么表？该查GJB 179A的表10，不但给出了每一方案的指标，而且画出了OC曲线。如果嫌表10不直观，可以自己算，可靠度单侧置信下限表和抽样检验数表都是用公式(4)或(5)算出来的。公式不是解析式，要反复试凑，麻烦一些，可用可编程计算器编程计算，亦可找到PC机实用程序。本文附表用公式(4)分别算出了通过置信水平0.9的成功率R0、通过置信水平0.1的成功率R1，可供实用。查附表R1，或者查GJB 4087可靠度单侧置信下限表[9]γ=0.9的RL，结果相同，由此可以反证附表的正确性。

2.4引信可靠性考核方法

1)有可靠性指标，凭抽样判断是否达标

有可靠性指标，要通过抽样考核一次性使用产品的可靠性是否达标，有三种方法：

①全数检验。将整批产品全部投入试验，查看可靠性真值。对整批引信追踪统计可以做到全数检验，只是旷日持久，要到训练、演习消耗完之后才能完成，并且需要管理到位。鉴定试验应尽可能扩大样本，向全数检验靠拢。例如，鉴定批全部投入试验、以综合判据检查试验总量、采取序贯抽样或GJB 179A的七次抽样，以及加入同一技术状态下的鉴定前试验量等。

②制定抽样方案。使用GJB 179A提供的方法。亦可使用本文所附速查表，只有一页纸，更便捷。为了运用自如，需要吃透GJB 179A的表10，明白可靠度R0与接收质量限AQL的互补关系。例如AQL 2.5意味着可靠度0.975或正常作用率97.5%。

③统计检验。使用GB/T 4088提供的假设检验方法。

2)没有可靠性指标，凭抽样估计产品可靠性

在没有可靠性指标，仅凭抽样结果估计产品可靠性时才用参数估计。查可靠度单侧置信下限表作区间估计(只要概念清楚，GJB 179A表10亦用可作区间估计)，或用样本观察值作点估计。只是要明白，区间估计置信下限RL与可靠性下限R0不是一回事。查出来的不是产品可靠性，而只是其可能出现区间的下限RL(上限RU≡1)。区间估计结果只是图1中包含了灰色地带的可能区间，对区间估计的不靠谱要心中有数，当样本达到四五十以上时，莫如相信点估计。

2.5可靠性指标的精度

GJB 179A的可靠性常用档次只有0.990、0.985、0.975、0.960、0.935、0.900；GB/T 4088的可靠性常用档次只有0.99、0.98、0.97、0.95、0.90，很粗，这是因为抽样检验有概率散布，精度本身就很差。量衣服不需要卡尺，提指标按GJB 179的分档已足够，再“精确”无实际意义。

公式(1)(2)(3)(4)均为二项分布式，许多数表也由此算出，但批量很小和不满足总量N≥10n时，误差较大。如果要精确，应当用超几何分布式(5)代替，此式看似复杂，在x较小时，函数计算器即可轻易算出，要诀在于先充分约分。GJB 179A的数表也由二项分布式算出，GB/T 13264-2009[10]相当于GJB 179A的超几何分布版。

3可靠性考核实例

3.1抽样方案

只要有了抽样检验方案，可靠性是否达标按判据执行，不存疑义。GJB 179A是有关计数抽样检验的唯一国军标，美军可靠性指南[8]也要求用GJB 179A蓝本的105标准。

3.1.1仅知道总量、用途和可靠性指标订方案

已知：批量N=5 000；可靠度R0=0.95，置信度(1-α)=0.9。

1)以故障率表达可靠性检验指标R0，AQL=1-R0=5(%)；

2)将AQL靠入接近的档(10、6.5、4.0、2.5、1.5、1.0)：高靠到4.0(%)档；

3)查GJB 179A表1：对于大批交验按S-2或S-3档，对于鉴定试验按S-4档。对于N=5 000按 S-2选取字码D；

4)查GJB 179A表2-A，字码D行，AQL 4.0列，查得正常方案(13,1)，查表3-A、表4-A或表10-E-2还可查到等效的二次抽样及七次抽样方案。

5)如果需要加严，查GJB 179A表2-B，字码D，AQL 4.0列查得加严方案(20,1)……

说明：

1) 抽样检验本来要有两对指标才能制定方案(现行错误方法凭一对指标查可靠性单侧置信下限表居然能定方案，是缺乏常识的笑料)，GJB 179表面上只依据接收质量限AQL，未考虑拒止指标LQ。实际上该标准根据统计经验，已将LQ隐含在批量、检验水平、加严与放宽的选择中。AQL=1.5%时，LQ在10%左右；AQL=2.5%时，LQ在15%左右；AQL=4%时，LQ在20%左右；AQL=6.5%时，LQ在35%左右。此例中，正常与加严方案的通过指标均为AQL 4.0(R0=0.96)，正常与加严是在调整拒止指标LQ(R1)，由表10或可靠度单侧置信下限表可查出，拒止指标R1分别为0.73和0.82。

2) DRP系列的迫击炮触发引信等产品的实验室试验和靶场试验就全部按GJB179A列出了检验水平、AQL和正常、加严和放宽抽样方案，并且正确表述了二次抽样方案(不再称为“加试”、“复试”)。说明这样做是可行的。我们大部分产品的实验室试验也已经用了GJB 179A，但大多数同志却不知道AQL=4.0(%)已经是“置信度0.9-可靠度0.96”。

3) 本文所附速查表亦可胜任，但一对指标不能确定方案，可以查到满足可靠性指标的一系列备选方案，并且同时查到拒止指标：

由R0=0.95查速查表，可以找到的方案有(11,1)、(22,2)、(35,3)、(49,4)、(64,5)。并且可以查出其R1分别为0.690、0.776、0.819、0.844、0.860。

核对：用GB/T 4087可靠度单侧置信下限表查出的分别是0.689 737 2、0.775 767 7、0.818 983 9、0.843 473 7、0.859 910 9，除小数取位外，二者完全相同，表明本文附表无误。

3.1.2知道总量和成对抽样检验指标制定方案

在既有战技指标中的接收指标R0，又有鉴定大纲、生产技术条件等二级文件中提供的拒止指标R1时，依据GJB179A查表，这是国际通行做法。例如：

已知：批量N=5 000；可靠度R0=0.95，通过置信度(1-α)=0.9；拒止成功率R1=0.80，拒止置信度γ=0.9。

1)以不合格率表达指标：AQL=1-R0=5(%)，高靠为4(%)，接收概率Pa=(1-α)=0.9；LQ=1-R1=20(%)，接收概率Pa=(1-γ)=0.10。

2)翻阅表10-□-1各表，找到表10-G-1的AQL 4.0列、Pa0.10行有最接近20的19.7，选定表10的G系列。

3)查表10-G-2，由AQL 4.0列得到一次抽样方案(32,3)、二次抽样方案(20,1,4；40,4,5)以及七次抽样方案。

说明：本文附表亦可使用：由R0=0.95查表，最接近的是(35,3)；由R1=0.80查表，最接近的是(32,3)。

3.1.3由抽样方案查抽样检验指标

方案与指标是严格对应的，无论懂与不懂，方案一确定，指标早就确定了。已有抽样方案，欲知其接收与拒止指标，可查GJB 179A表10。例如：

已知抽样方案(13,0)。默认α=β=0.1，即AQL的接收概率Pa=0.90、LQ的接收概率Pa=0.10。

1)翻阅GJB 179A表10-□-2，寻找有(13.0)方案的表，找到表10-E-2，在AQL 1.0列。

2)查表10-E-1，AQL 1.0列，Pa0.90行查到AQL=0.807(%)≈1(%)、Pa0.10行查到LQ=16.2。

3)换算为方案的可靠性检验指标：通过置信度0.9-可靠度0.992；拒止置信度0.9-拒止成功率0.838。

说明：

1)本文附表用起来更直接：由n=13行Ac=0列查到R0=0.992，R1=0.838。

2)(5,0)、(8,0)、(13,0)是靶场试验中炮口安全性试验的常见方案。0.008 07远远不能满足考核延期解除保险距离内0.001解除保险(AQL=0.1%)的要求，(5,0)、(8,0)差得更远。所以一般试验表此项AQL栏都空着，以“致命缺陷一票否决”论蒙混过关。其实查附表，(70,0)才能满足AQL 0.1%。(13,0)的一票否决可信度不够，代替不了(70,0)的一票否决。舍不得加大样本，只能通过多批累计解决，应当写明AQL=0.1(%)，同时说明连续6批满足(13,0)，符合综合判踞才能下安全结论。安全性尚可如此，其他指标也不必追求一口吃个胖子，规定各组的综合判据、瞻前顾后地加严放宽等都体现累计的思想。

3.2拒止判据法假设检验

这是GB/T 4088推荐的方法，称为“单侧检验拒绝域上限c2”，即方案的拒止判据Re[1]。

已知：样本n=40，不合格数x=1，可靠性检验指标p0=0.01(AQL=1%)。

可以用公式(2)算出c2。查表更简便，查GB/T 4088表E.1，n=40行，p=0.01列，得c2=2，x

说明：

1)该表的涵义为样本40，故障2或更多，才能否定故障率不高于指标的假设，因此结论是达标。其实质是使用方案(40,1,2)检验可靠性是否达到0.987(≈0.99)。

2)表E.1样本量最多50，要查更大样本可使用本文所附速查表插值。方法：R0=1-p0=0.99，由速查表n=40行、找与R0=0.99最接近的列，得到通过判据Ac=1，拒止判据c2=Ac+1=2(与表E.1结果吻合)。

3.3接收概率法假设检验

已知指标：可靠度R0=0.94，置信度(1-α)=0.9；样本73发，故障4发。

首先按文献[4]要求将指标可靠度和置信度 “翻译”为故障率指标p0，显著性水平α为0.1。

将p0=1-0.94=0.06、n=73、x=4代入公式(3)，算出P=0.635；满足P>α，结论：产品达标。

4结论

本文再次证明引信可靠性考核中，由抽样判断引信可靠性是否达标或由可靠性指标制定抽样方案时，查可靠度单侧置信下限表是错的，系统性错误。错在该表的“置信度”是拒止置信度，查出的不是“接收置信度0.9的可靠度”，而是“接收置信度0.1的可靠度”，与能否达标无关。这种做法没有法理依据，只是以讹传讹的习惯性错误。

据此，本文提出执行GJBz 20119时，将“可靠度-置信度”指标理解为“可接收成功率-通过置信度”。考核可靠性时，依据GJB 179A制定方案进行抽样检验、依据GB/T 4088-2008进行假设检验，或者查本文附表。可靠度单侧置信下限表只适用于没有可靠性指标时作区间估计以及查拒止指标，不可张冠李戴。

DRP系列迫击炮引信验收试验的实例和本文的算例表明，将“可靠度-置信度”指标理解为“可靠性-通过置信度”是可行的，用GJB 179A和GB/T 4088考核引信可靠性是可操作的。算例还表明本文所附速查表数据无误，并且使用起来更便捷(见第8页附表)。

参考文献:

[1]张龙山.以成功率表述引信可靠性指标[J].探测与控制学报,2013,35(6):1-5.

[2]GJB 451A-2005 可靠性维修性保障性术语[S].北京：中国人民解放军总装备部,2005.

[3]GJB 450A-2004 装备可靠性工作通用要求[S].北京：中国人民解放军总装备部,2004.

[4]GB/T 4088-2008 数据的统计处理和解释 二项分布参数的估计与检验[S].北京：中华人民共和国质量监督检验检疫总局/中国国家标准化管理委员会,2008.

[5]GJBz 20119-93 炮兵引信战术技术指标通用要求[S].北京：中国人民解放军总参谋部,1993.

[6]GJB 376-87 火工品可靠性评估方法[S].北京：国防科学技术工业委员会,1987.

[7]GJB 179A-96 计数抽样检验程序及表[S].北京：国防科学技术工业委员会，1996.

[8]RAM Guide (DOD GUIDE FOR ACHIEVING RELIABILITY, AVAILABLITY, AND MAINTAINABILITY)[S].US：System Engineering for Mission Success，2005.

[9]GB/T 4087-2009数据的统计处理和解释二项分布可靠度单侧置信下限[S].北京：中华人民共和国质量监督检验检疫总局/中国国家标准化管理委员会，2009.

[10]GB/T 13264-2008 不合格品百分数的小批计数抽样检验程序及抽样表[S].北京：中华人民共和国质量监督检验检疫总局/中国国家标准化管理委员会，2008.

附表　抽样检验指标速查表

注：R0为可靠性指标“可接收成功率”，R0=1-AQL；R1为拒止指标“拒止成功率” (与“可靠度单侧置信下限”相同)，R1=1-LQ；α=β=0.1(置信水平0.9)。

*收稿日期:2016-03-22

作者简介:张龙山(1942—),男，江苏泗洪人，研究员，研究方向：引信技术。E-mail:tcykz@263.net。

中图分类号:TJ430

文献标志码:A

文章编号：1008-1194(2016)03-0001-08

Systematic Error of Fuze Reliability Test and Statistic Test Principles

ZHANG Longshan

(Science and Technology on Electromechanical Dynamic Control Laboratory, Xi’an 710065，China)

Abstract:Aiming at the fault using of the reliability one-side confidence lower limit table in fuze reliability test, the systematic error was testified when using the table to judge weather the fuze reliability is qualified. In fact, the “confidence” in this table meant “reject confidence”, the misusing of the concept was out of legal basis. It was proposed that taking the “reliability-confidence” index as the “reliability-passing confidence” when using GJB179A. The reliability test sample scheme and the hypothesis testing scheme should be made according GJB179A and GB/T4088-2008. The reliability one-side confidence lower limit was only used as interval estimation or rejecting index. This practice was testified in DRP serial products examples in this paper.

Key words:fuze; reliability; confidence level; hypothesis testing