基于改进GM(1，1)模型的引信系统贮存寿命预测方法

戴宗亮,李小兵,吴博文,曹　艳

(空军工程大学防空反导学院，陕西 西安 710051)



基于改进GM(1，1)模型的引信系统贮存寿命预测方法

戴宗亮,李小兵,吴博文,曹艳

(空军工程大学防空反导学院，陕西 西安 710051)

摘要:针对引信系统复杂、贮存样本量受限、测试数据波动性较大等问题，提出了基于改进GM(1，1)模型的引信系统贮存寿命预测方法。该方法在利用“指数-对数变换”对原始数据预先进行光滑处理的基础上，通过建立GM(1,1)模型和残差修正模型，推导出对引信系统贮存寿命预测的改进算法。实例分析表明，该方法具有预测精度高、适用范围广、通用性强等优点，可推广用于类似系统或设备的寿命预估。

关键词:引信；寿命预测；指数-对数变换；GM(1，1)模型；残差修正

0引言

对武器装备的可靠性和贮存寿命进行及时准确预测，是动态掌握武器系统使用性能和健康状态的主要途径，也是装备管理与维修领域研究的重要理论问题。引信作为导弹的重要组成部分，在弹目遭遇中发挥着举足轻重的作用，其性能的优劣直接影响着导弹的战技指标，进而影响战争形态。而引信系统的全寿命周期中，由于受周围环境应力和人为因素的影响，使设备性能参数发生变化，进而导致整个系统得可靠性降低甚至功能失效[1]。因此，对引信系统的贮存寿命进行及时准确有效地预测具有重要意义。

在引信的可靠性评估方面，国内外一直应用系统可靠性的评估方法。文献[2]的王宏洲博士应用了经典的统计和经验Bayes方法研究了引信环境因子以及可靠性评估。文献[3]应用了加速试验的方法研究了引信的可靠性评估，文献[4]应用了CMSR方法和混合的Bayes方法对引信的可靠性进行了评估，文献[5]应用了灰色理论对引信的贮存可靠性进行了预测。文献[6]根据灰色理论的特点，将灰色模型引入到了加速试验机理一致性判定。这些方法均在一定程度上对引信的可靠性进行了评估，但在对于整个引信系统的评估方面仍有一定的局限性，比如对于预测精度，小样本，特别是测试数据波动性等仍不能较好的满足要求。本文针对上述问题，提出了基于改进GM(1，1)模型的引信系统贮存寿命预测方法。

1改进的GM(1,1)模型

1.1原始GM(1,1)模型建立

根据GM(1,1)模型建模机理[7]，设有原始数据序列：

x0(t)={x0(1),x0(2)，x0(3)，…,x0(n)}

(1)

将原始数列做1-GAO(一次累加生成)，生成数列：

x1(t)={x1(1),x1(2)，x1(3)，…,x1(n)}

(2)

建立一阶线性微分方程模型为：

(3)

式(3)中，a,u为待求参数，其中a为发展系数，u为灰色系数。

利用最小二乘法求出式(3)中的a,u，其具体步骤可参考文献[8]。

(4)

式(4)中,

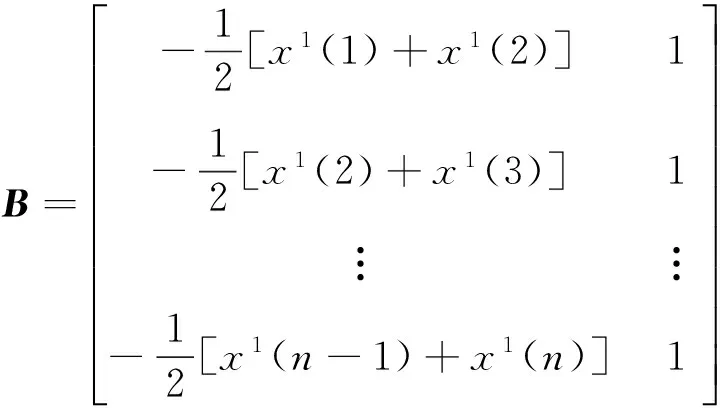
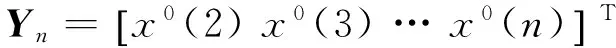
k=(1,2,…,n)

(5)

再作一次累减生成(1-IAGO)，得预测模型:

k=(1,2,…,n)

(6)

即：

k=(1,2,…,n)

(7)

1.2GM(1，1)模型的改进

对原始序列进行复合变换后的数据序列建立的灰色模型所得预测精度高于传统做法[9]。本文利用指数-对数变换处理原始数据，改善数据列的光滑程度，提高预测精度。

1.2.1对原始数据的“指数-对数变换”

引信的可靠性数据序列不是递增的，而是随着时间的推移，其数据递减的，则可以用

x″0(k)=ax′0(k),a>1

(8)

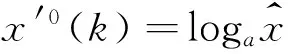
证明：设x(1)>x(2)>…>x(n)，则-x(1)<

-x(2)<…<-x(n),

∵-x(k)为递增数列,∴a-(-x(k))=ax(k)

(a>1,k=1,2,…,n)得证。

若定理条件不满足，可通过把整个序列同时加上一个合适的正常数，即x′0(k)=x0(k)+c，k=(1,2,…,n)，使x′0(k)>1，对x′0(k)进行预测，最后用x0(k)=x′0(k)-c还原即可。

1.2.2残差修正模型

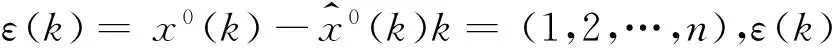
(10)

2贮存寿命预测方法

2.1引信系统贮存寿命预测方法建模

引信贮存可靠性是指引信在规定的储存条件下、规定的储存时间内,保持规定功能的能力。其中包含了三个方面,即规定的储存条件,主要是指储存状态(密封、非密封)和储存环境条件(温度和湿度);规定的储存时间,主要是指合格的引信从入库到准备使用为止的这段时间;规定的功能,主要是指引信原有的战技指标。

根据导弹引信的自身特点,可选择以下一些数量指标作为引信贮存可靠性的评估指标。如贮存可靠度，贮存失效率函数，平均贮存寿命，可靠贮存寿命等，本文选取贮存可靠度作为研究预测，其余方法类似。

根据上述GM(1,1,)模型的改进方法，结合引信可靠性数据，对引信系统贮存寿命预测方法建模，具体步骤如下：1) 利用式(8)对引信已知可靠性数据进行“指数变换”，进行光滑处理；2) 将进行光滑处理后的数据利用原始GM(1,1)模型进行建模计算，得到可靠性预测值及残差；3) 利用式(8)对残差进行指数变换后，建立残差GM(1,1)模型，得预测残差值，再利用式(9)进行还原；4) 利用式(10)去修正可靠性预测值；5) 利用式(9)对修正后可靠性预测值进行“对数变换”，即得最终预测结果；6) 根据引信的贮存可靠度下限来预测引信的贮存寿命。

2.2模型的检验

为确保所建立的GM(1，1)模型有较高的预测精度，还需要进行以下模型检验:

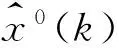
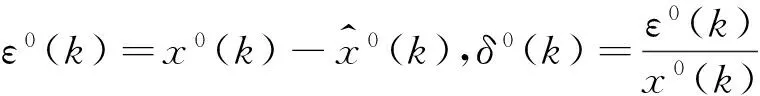
(11)

随着时间的推移，由于环境等各种因素影响，导致预测精度的降低，所以及时有效的补充灰平面，提高白平面至关重要。具体做法是，根据已知数列建立GM(1，1)模型，预测一个灰数值，然后将这个预测值补充在已知数列之后，构成新信息数列[11]，即

x0(t)={x0(1),x0(2),…,

x0(n),x0(n+1),…}

(12)

这种预测方法称为“增维灰数递补动态预测”。

3应用实例

连续五年定期测量的贮存可靠性如表1，引信的可靠度下限规定为0.90。

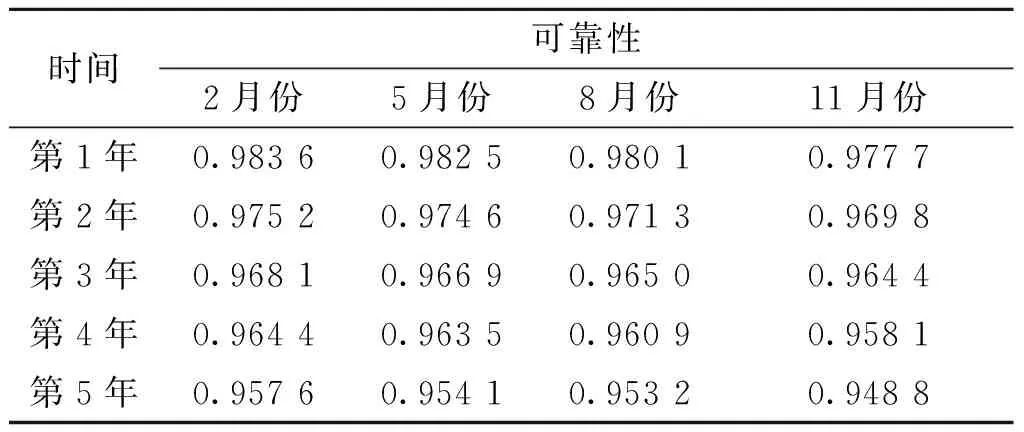
表1　连续五年定期测量的贮存可靠性

3.1原始模型预测

原始序列为：x0(k)={0.983 6,0.982 5,0.980 1,0.977 7,0.975 2,0.974 6,0.971 3,0.969 8,0.968 1,0.966 9,0.965 0,0.964 4,0.964 4,0.963 5,0.960 9,0.958 1,0.957 6,0.957 6,0.954 1,0.953 2,0.948 8}

根据灰色预测理论得：

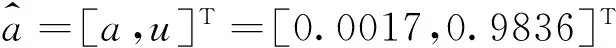
0.9827e-0.0017k,k=(1,2,…,n)。

(13)

3.2改进模型预测

由于原始序列0≤{x0(k)}≤1，k=(1,2,…,20)，则根据建模理论，将原始序列{x0(k)}k=(1,2,…,20) 均加个常数1， 得{x′0(k)}。

对{x′0(k)}k=(1,2,…,20) 作指数变换ax′0(k),a>1得{x″0(k)}k=(1,2,…,20)(取a=1.25)，再对{x″0(k)}k=(1,2,…,20)做一次累加。

根据前面讨论的灰色预测模型方法计算可得：

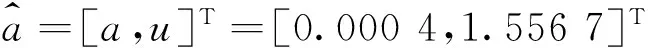
1.556 3e-0.0004k,k=(1,2,…,n)。

(14)

据式(8)计算得残差为ε={0 0.0011

根据残差修正模型对残差修正，建立残差模型如下：

1.250211e0.000012976k,k=(1,2,…,n)。

(15)

0.975 60.973 90.972 30.970 60.969 0

0.967 30.965 70.964 00.962 40.960 7

0.959 10.957 40.955 70.954 10.952 4

0.950 8}

3.3模型的检验

由此可得改进模型的预测精度更好，效果更好。将改进模型进行外推扩展仿真，以此预测该导弹引信的贮存寿命。

根据图3，由于引信的可靠度规定下限0.90，得出该引信的贮存寿命为12.50年，也就是引信还可能贮存7.50年。

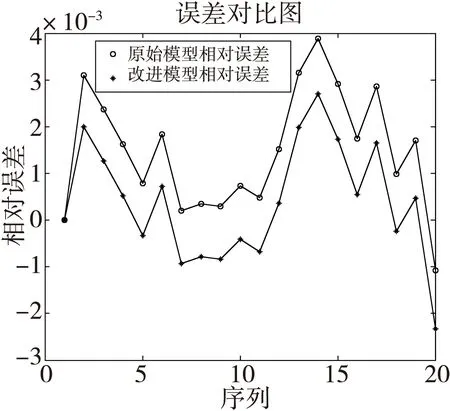
图1　各模型相对误差对比图Fig.1　Relative residuals of each model contrast figure

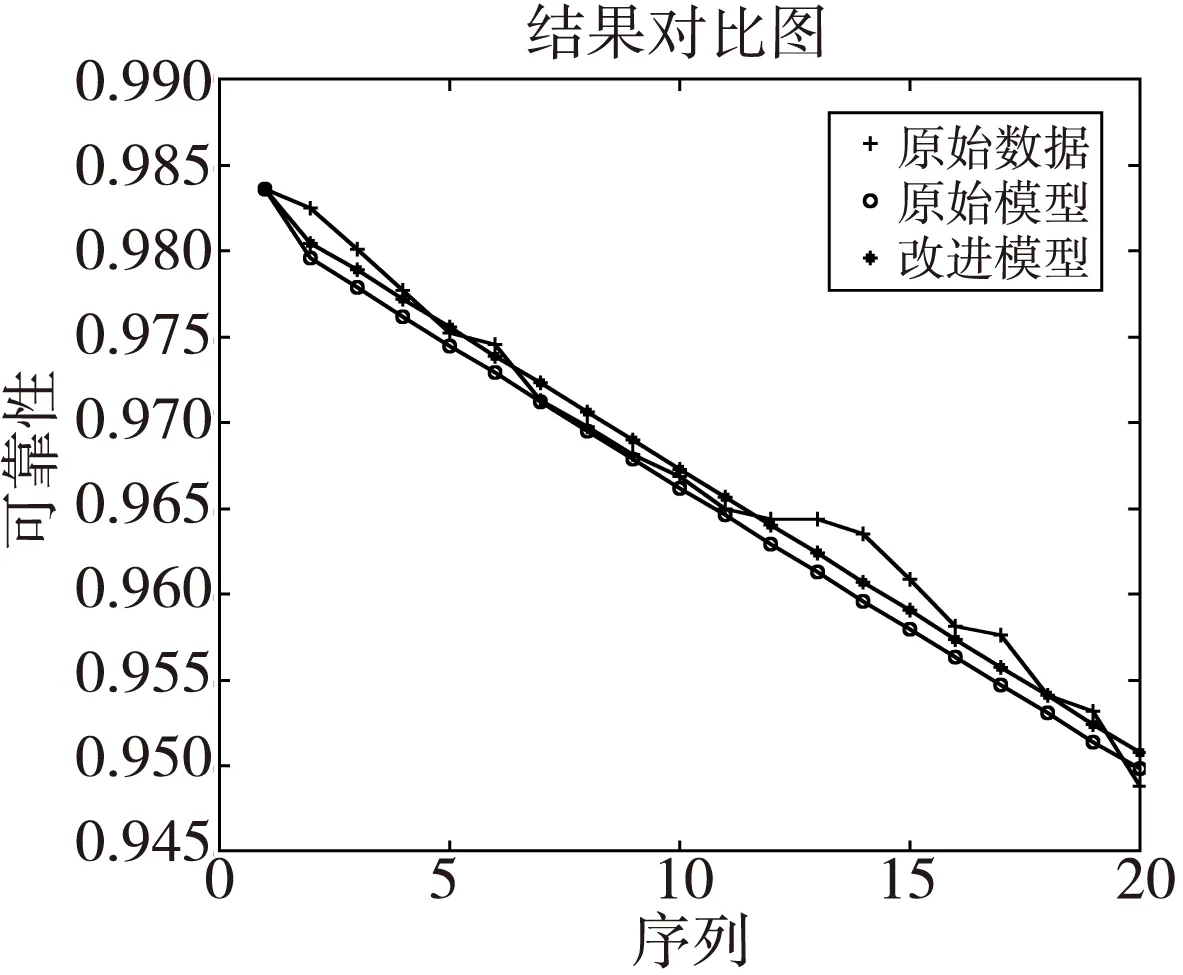
图2　各模型预测结果与原始数据对比图Fig.2　Each model predicted results compared with the original data

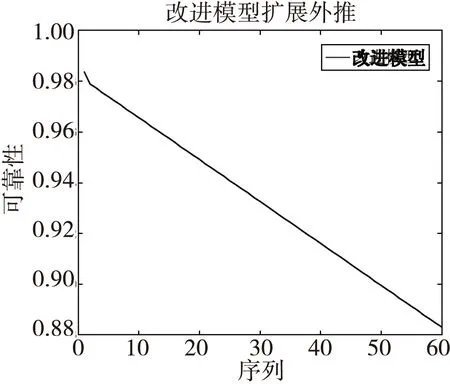
图3 贮存可靠性预测Fig.3　The forecasting of storage reliability

4结论

本文提出了基于改进GM(1，1)模型的引信系统贮存寿命预测方法。该方法在利用“指数-对数变换”对原始数据预先进行光滑处理的基础上，通过建立GM(1,1)模型和残差修正模型，推导出了对引信系统贮存寿命预测的改进算法。实例分析表明，该方法具有预测精度高、适用范围广、通用性强等优点，可推广用于类似系统或设备的寿命预估。

参考文献:

[1]张亚,徐建军,赵河明.弹药可靠性技术与管理[M].北京:兵器工业出版社. 2001.

[2]王宏洲.环境因子估计理论与引信可靠性评估研究[D].北京：北京理工大学，1991.

[3]张亚，赵河明，董少峰.无线电引信贮存寿命预测方法研究[J].探测与控制学报，2001,23(4):374-379.

[4]王玮.引信可靠性评估方法的研究[D].石家庄：军械工程学院，2006.

[5]赵铮,刘丽群. 基于灰色系统理论的引信储存可靠性预测模型[J]. 探测与控制学报,2013,35(5):46-48.

[6]潘晓茜,康锐. 基于灰色预测的加速试验机理一致性判定方法[J]. 北京航空航天大学学报,2013,39(6):787-792.

[7]Wang Yuhong,Liu Qin, Tang Jianrong, et al. Optimization approach of background value and initial item for improving prediction precision of GM(1,1) model[J]. Journal of Systems Engineering and Electronics, 2014, 25(2):77-82.

[8]刘玉梅,蒋寿生,袁文华. 锅炉过热器剩余寿命非等间隔灰色预测[J].中南大学学报(自然科学版)，2010,41(3):1202-1206.

[9]王聪.网络空间嵌入模型与应用研究[D].成都：电子科技大学，2013.

[10]何斌,蒙清.灰色预测模型拓广方法研究[J].系统工程理论与实践，2009，22(9):137-140.

[11]陈尚东，张琳，陈永革. 地空导弹武器系统维修费用灰色预测模型[J]. 空军工程大学学报(自然科学版)，2008，9(2)：72-75.

*收稿日期:2015-12-21

基金项目:陕西省自然科学基金项目资助(2012JM8020)

作者简介:戴宗亮(1992—),男，四川冕宁人，硕士研究生，研究方向：可靠性评估和贮存寿命预测。E-mail:dykylb511@163.com

中图分类号:TJ430.6

文献标志码:A

文章编号：1008-1194(2016)03-0086-04

Fuze Storage Life Forecasting Based on Improved Grey Model

DAI Zongliang，LI Xiaobing，WU Bowen，CAO Yan

(Air and Missile Defense College，Air Force Engineering University， Xi’an 710051，China)

Abstract:Considering fuze system reliability test data have the features of small sample and large random fluctuations, this paper introduced an improved grey model in fuze storage life forecasting. By smoothing the original data sequence, and building GM models to residuals for updating the forecasting data. The analytic results indicated that the methods were better than the original forecasting method, and were regarded of feasibility and high practice value.

Key words:fuze;life forecasting;power function-logarithm function compound transformation; grey forecasting model; update residuals