基于改进引力搜索的武器目标分配方法

李槟槟，何广军，张明亮，尤晓亮，田德伟

(空军工程大学，陕西 西安 710051)



基于改进引力搜索的武器目标分配方法

李槟槟，何广军，张明亮，尤晓亮，田德伟

(空军工程大学，陕西 西安 710051)

摘要:针对目前武器目标分配(WTA)问题所用引力搜索算法(GSA)存在着早熟收敛的问题，提出了基于改进GSA的武器目标分配方法。该方法首先将粒子群算法(PSO)的记忆信息和群体共享信息能力引入到GSA算法之中，再将混沌搜索(CS)的思想嵌入到改进的GSA算法之中，提出了CP-GSA算法；然后利用提出的CP-GSA算法直接求解WTA最小化问题，进行武器目标分配。仿真实验表明：所提出的方法能够有效解决WTA问题，提高分配性能，在4个地面防空作战单元抗击8个来袭目标的情况下，迭代41次即可得到最优解，适应度值为1.18，与枚举法所得的最优适应度值相等。

关键词:武器目标分配；引力搜索算法；粒子群算法；混沌搜索

0引言

武器目标分配(WTA)问题是现代信息化战争中十分重要的问题[1]，但是由于它的解空间大小随着武器和目标数量的增加而呈指数增加，因此是一个NP完全问题，需要寻求快速、有效的方法以满足实时需要。目前，智能算法被广泛应用到WTA的求解之中，如遗传算法[2](GA)、蚁群算法[3](ACA)、PSO算法[4-6]和人工免疫算法[7](AIA)等。

GSA算法[8]是伊朗的克曼大学教授EsmatRashedi等人于2009年提出的新型智能算法，其全局搜索能力明显优于现有PSO算法、GA算法等仿生智能优化算法，受到了人们的普遍关注和研究，因此，将GSA算法应用到WTA问题的求解之中具有较大潜力。但是，与其他进化算法一样，现有GSA算法不可避免地存在着早熟收敛问题，影响了利用GSA算法求解WTA问题的收敛速度和精度。本文针对上述问题，提出了基于改进GSA的武器目标分配方法。

1WTA问题模型和引力搜索算法

1.1WTA问题模型

假设J个地面防空作战单元联合抗击K个空中目标，WTA问题的求解是要确定分配给各目标的不同作战单元武器的数量，以使得所有目标的总期望生存值最小。因此，WTA问题可以描述求解X的最小化问题：

(1)

式(1)中，X是由xjk,j=1,2,…,J;k=1,2,…,K构成的矩阵；ωk为第k个目标的威胁值；xjk≥0为第j个火力单元分配给第k个目标的武器数；pjk为第j个火力单元对第k个目标的杀伤概率；Vk为分配给第k个目标的最大武器数目；Uj为给第j个火力单元可分配的最大武器数目。

求解WTA问题，首先需要确定模型中的各个参数，其中，目标的威胁值可以通过人工智能或者基于知识的专家系统等方法确定；武器对目标的杀伤概率与武器射击命中概率和目标防护能力等有关，可通过文献[7]给出的方法确定。

1.2GSA算法

假设引力系统有N个粒子，每个粒子的位置为：

Xi=(Xi1,…,Xid…,XiD), i=1,2,…,N

(2)

式(2)中，Xid为第i个粒子在第d维上的位置。

根据牛顿万有引力定理，在时刻t，第i个粒子在第d维受第j个粒子的作用力大小为：

(3)

式(3)中，Mi(t)和Mj(t)分别为粒子j和粒子i的引力质量，G(t)是在t时刻的引力常数，可以表示为：

G(t)=G0exp(-αt/T)

(4)

其中G0=100，α=20，T是最大迭代次数。

根据适应度函数，在引力质量与惯性质量相等的假设下，粒子引力质量可定义为：

(5)

其中，fiti(t)为t时刻粒子i的适应度值，fitbest(t)和fitworst(t)为群体最优和最差适应度值，对于求最小值问题，fitbest(t)和fitworst(t)定义为：

(6)

在实际中，引力质量一般单位化为：

(7)

因此，第i个粒子在第d维上受到总作用力是其他所有粒子作用力的总和：

(8)

根据牛顿第二定理，在时刻t，粒子i在第d维上的加速度aid(t)可以表示为：

aid(t)=Fid(t)/Mi(t)

(9)

在时刻t+1，粒子速度及位置更新为：

(10)

其中，rand是[0,1]之间的随机数。

假设最大速度为Vmax，最小速度Vmin，在迭代的过程中，所有粒子的速度Vid(t)都应该在[Vmin,Vmax]区间中，即满足

(11)

引力搜索算法根据式(10)不断更新自身所在位置，直至达到迭代终止条件，此时，粒子所在的最好位置即为问题的解。

2基于CP-GSA算法的武器目标分配方法

从GSA算法的基本步骤可以看出，GSA在位置更新的过程中，只有个体当前位置在起作用，并没有利用群体之间的信息共享，因此，学者们提出将PSO算法的位置更新方法与引力搜索算法相结合，改善了性能，但在迭代后期容易陷入局部最优，使得算法收敛速度下降，求解精度有待进一步提高。因此，利用早熟判断机制，在改进的CS算法陷入早熟收敛时，进行混沌搜索，以跳出局部最优，提高收敛速度和精度。

2.1PSO算法

PSO算法，也称为微粒群算法[9]，是由美国Kennedy和Eberhart于1995年提出的一种基于群智能的随机搜索算法。该算法模拟鸟类的觅食行为，将优化问题的搜索空间模拟为鸟类的飞行空间，将每只鸟抽象成一个没有体积和质量的微粒，代表问题的一个候选解，将寻找问题最优解的过程比作寻找食物的过程，进而求解复杂的优化问题。

PSO算法的数学描述如下，假设种群规模为N，在迭代时刻t，每个粒子在D维空间中的坐标位置可以表示为Xi=(Xi1,…,Xid,…,XiD)；粒子的速度表示为Vi(t)=(Vi1(t),…,Vid(t),…,ViD(t))。坐标位置和速度在t+1时刻，按照下式进行调整：

(12)

式(12)中，w(t)为惯性权值，c1和c2为加速系数，均为正实数；rand表示在[0,1]内均匀分布的随机数；Pi(t)表示第i个粒子经历过的最好位置，G(t)表示所有粒子经历的最好位置。

可以看出，式(12)由3部分组成，第1部分为“惯性”部分，表示粒子保持先前的速度；第2部分为“认知”部分，表示粒子本身的思考，所以c1又称为认知系数；第3部分为“社会”部分，表示粒子间的信息共享与相互合作，所以c2又称为社会系数。

2.2CS算法

混沌状态一般是由确定性方程导出的具有随机性的运动，是自然界广泛存在的一种非线性现象。混沌运动看似随机，却是由确定的方程导出的，因此具有遍历性、随机性和规律性等特性，能在一定范围内按其自身规律不重复地遍历所有状态。因此，学者们提出利用混沌运动的这些性质进行优化搜索，以跳出局部最优，提高算法收敛速度。

2.3CP-GSA算法

根据上述分析，我们采用CS和PSO算法的群体信息共享改善引力搜索算法的性能，提出CP-GSA算法，使得粒子即遵守运动定律，又具有记忆和群体信息交流能力，在算法后期能够快速收敛。在CP-GSA算法中，粒子位置和速度的更新方式为：

(13)

其中，Pid(t)表示第i个粒子在在第d维上经历过的最好位置，Gd(t)表示所有粒子在第d维上经历过的最好位置。

当判定算法早熟后，利用CS算法使得算法跳出局部最优，混沌搜索中用到的混沌方程是Logistic方程，其表达式为：

Yi+1=μYi(1-Yi)|i=1,2,…;μ∈(2,4]

(14)

其中，μ为控制变量，当μ=4，初始值取值在[0,1]时，系统进入完全混沌状态。

混沌搜索的实现过程为：首先随机产生一个在[0,1]区间内的初始变量Y0=[Y01,…,Y0d,…,Y0D]；然后利用式(14)产生混沌序列Y1,Y2,…,YQ(Q为混沌搜索的最大迭代次数)，并把混沌区间映射到优化变量的取值区间；最后，对每个混沌变量计算其适应函数值，得到性能最好的可行解，随机取代群体中的一个粒子。

2.4CP-GSA求解WTA问题

在确定WTA模型中的各个参数后，利用所提出的CP-GSA算法求解WTA问题，即求解矩阵X。由于GSA算法是对向量进行求解的，用来求解矩阵存在速度的表示问题，因此，按照文献[5]的方法，我们用一个长度为U1+U2+…+UJ的整数串P表示一个粒子，即粒子的维数为D=U1+U2+…+UJ，第j个火力单元的分配方案对应于元素组：

PU1+U2+…+Uj-1+1,PU1+U2+…+Uj-1+2,…,PU1+U2+…+Uj

(15)

式(15)中，元素的取值为0到K之间的整数。若某一元素等于0，代表这个元素对应的武器未分配给任何目标；若某一元素等于k，则代表这个元素对应的武器分配给了目标k。因此，第j个火力单元分配给目标k的个数等于元素组(15)的取值中出现k的次数。

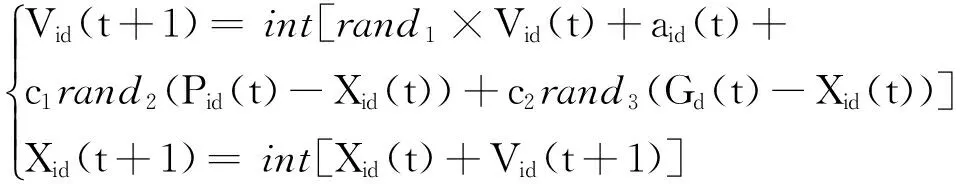
(16)

在利用CP-GSA算法求解WTA问题时，WTA问题的第一个约束条件在利用整数串P表示粒子的情况下已经得到满足；按照第二个约束条件，整数串P的元素值等于k的个数应不大于Vk，因此我们约定若大于Vk，则随机删除元素，使得元素值等于k的个数等于Vk，在这种情况下，最大速度和最小速度也是不需要设定的。

在上述条件下，WTA问题的求解等价于直接求解无约束最小化问题：

(17)

此时，利用CP-GSA算法求解WTA问题的适应度函数为：

(18)

其中，xjk是X的第(j, k)个元素。

因此，CP-GSA算法求解WTA问题的具体步骤为：

1)种群初始化：根据问题规模和变量个数确定种群大小N和维数D=U1+U2+…+UJ；随机设置粒子的初始位置X和初始速度V；设定最大迭代次数T、惯性权值w(t)、加速系数c1和c2以及混沌搜索的最大迭代次数Q。

2)粒子适应度评价：根据式(18)计算粒子的适应度值，更新每个粒子和种群在第d维经历的最好位置Pid(t)和Gd(t)。

3)早熟收敛判定：利用文献[10]的适应度方差方法对是否出现早熟进行判定，若出现早熟，转到步骤4)进行混沌搜索，否则，转至步骤5)。

4)混沌搜索：随机产生初始变量Y0，利用式(14)产生混沌序列，用性能最好的解随机取代群体中的一个粒子。

5)速度和位置更新：按式(16)对各个粒子的速度和位置进行更新。

6)约束条件判定：判断每个粒子的位置是否满足第二个约束条件，如满足转至步骤8)，否则，转至步骤7)。

7)删除多余元素：根据Vk, k=1,2,…,K随机删除多余的元素，使得粒子的各维取值等于k的个数等于Vk。

8)算法终止判定：根据算法终止条件或最大迭代次数对是否终止算法进行判定，若终止，则结束优化，返回全局最优解，否则，转至步骤2)。

利用CP-GSA算法求解WTA问题的流程图如图1。

3仿真实验

本部分对所提方法的有效性进行验证，并与利用PSO算法和GSA算法求解WTA问题的性能进行对比。

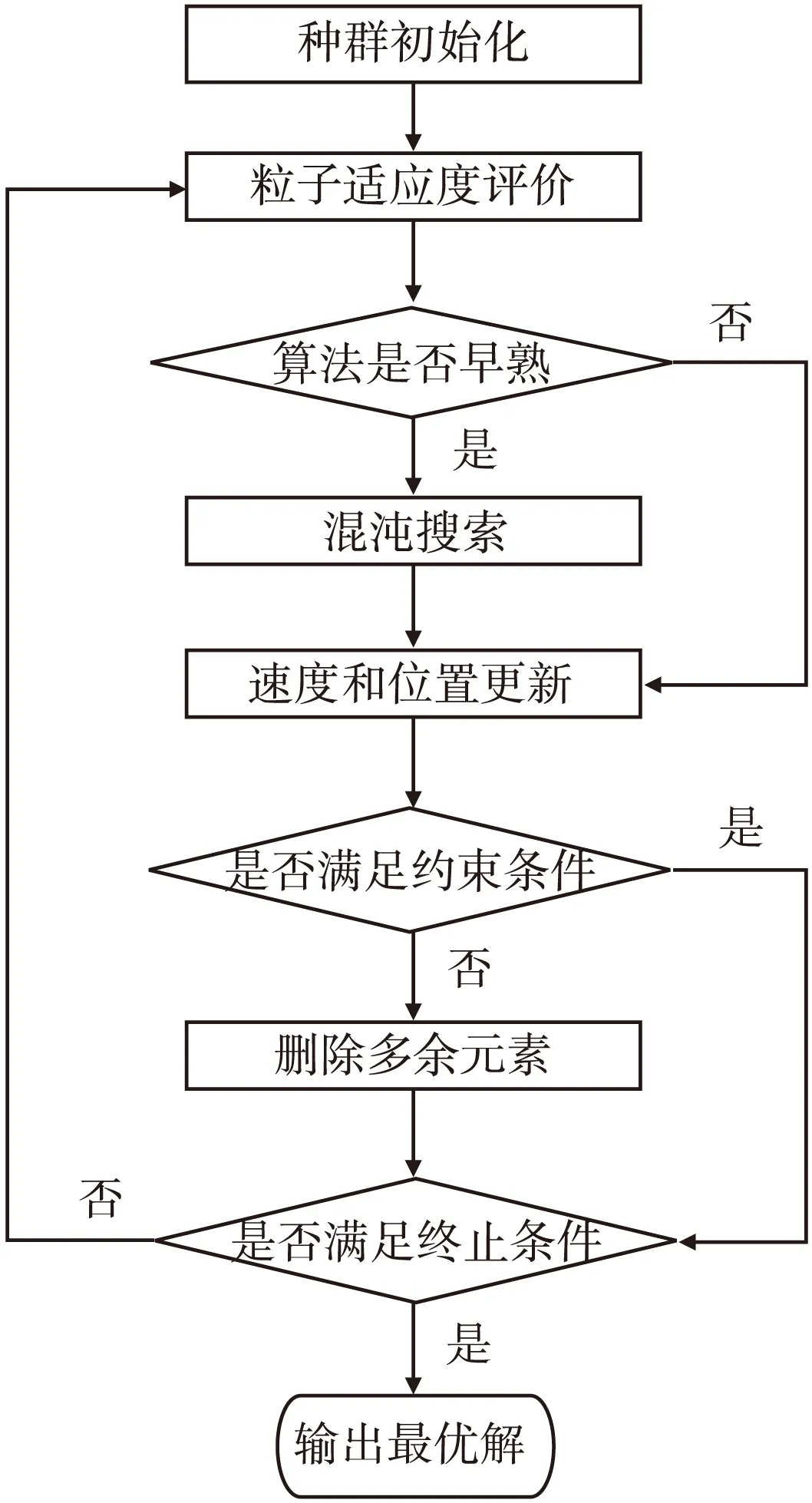
图1　CP-GSA求解WTA问题流程图Fig. 1　The flow chart of CP-GSA for solving WTA problem

假设由4个地面防空作战单元抗击8个来袭目标，4个作战单元具有的武器数分别为{3, 1, 2, 2}，每个目标最多可分配1个武器。目标的威胁系数和各类武器对各来袭目标的单发杀伤概率分别如表1和表2所示。

表1　目标威胁系数

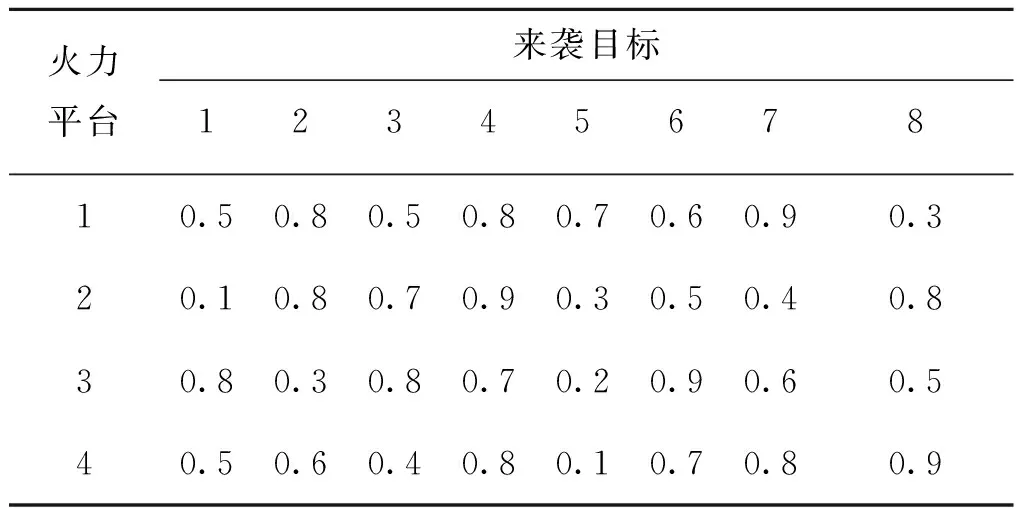
表2　武器对目标的杀伤概率

CP-GSA算法的参数设置为：粒子数N=50，最大迭代次数T=200，加速系数c1=c2=2，混沌迭代次数Q=50。利用CP-GSA算法求解WTA问题，在第41代得到最优解，适应度值为1.18，与枚举法所得最优适应度值相等，最优分配方案如表3所示。

表3　最优武器目标分配方案

表3中的分配方案表示：火力平台1的武器迎击目标2、目标5和目标7；火力平台2的武器迎击目标4；火力平台3的武器迎击目标1和目标3；火力平台4的武器迎击目标6和目标8。

对利用PSO算法、GSA算法和CP-GSA算法求解WTA问题分别运行50次，可以得到不同算法最优分配方案的适应度值情况如表4所示。运行200次，得到三种不同算法的收敛曲线如图2所示。

表4　不同分配方法的适应度值情况

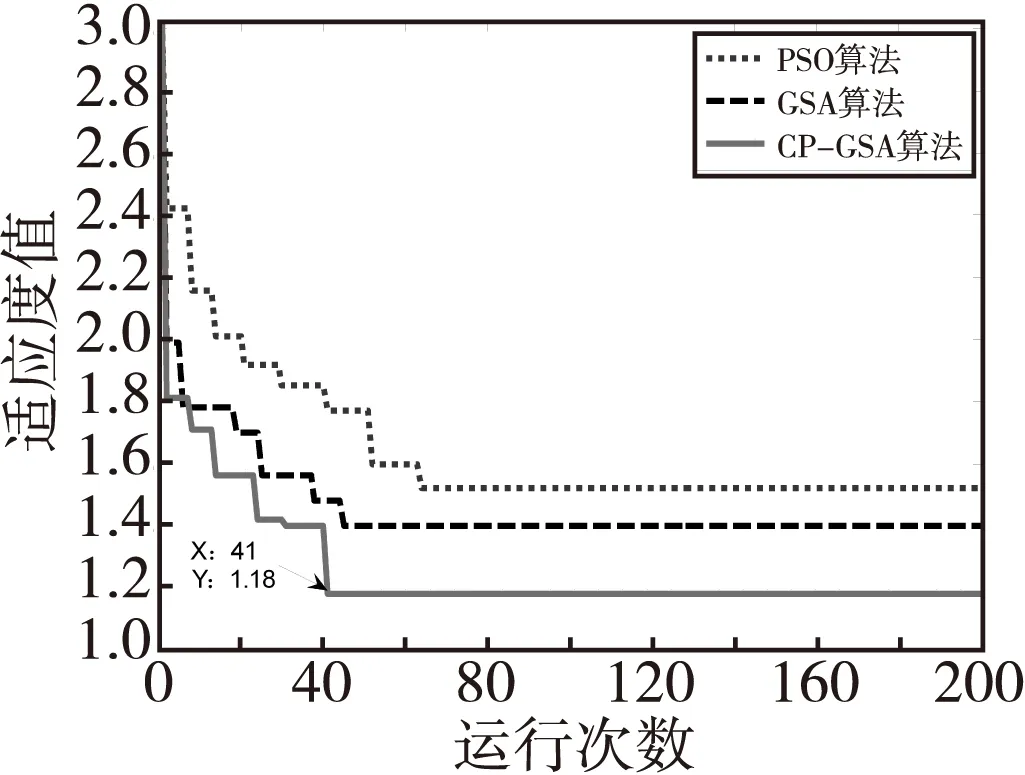
图2　算法收敛曲线Fig.2　The curves of algorithms’ convergence

从表4和图2可以看出，CP-GSA算法的性能最优，GSA算法次之，PSO算法最差。这是由于PSO算法和GSA算法的粒子在算法后期陷入了局部最优，算法性能有待提高，而CP-GSA算法中的粒子既遵守运动定律，又具有记忆和群体信息交流能力，在算法后期利用混沌搜索使得算法能够快速跳出局部最优、快速收敛，在保证全局搜索能力的情况下，提高了局部搜索能力。

4结论

本文提出了利用改进GSA算法求解武器目标分配问题的方法。该方法将PSO算法的种群信息共享和CS算法融入到引力搜索的迭代过程之中，解决了GSA算法易陷入局部最优的问题，提出了改进的GSA算法，并将其直接应用到WTA问题的求解之中。仿真实验表明，所提方法能够快速、准确求解WTA问题，以较少的迭代次数即可获得有效分配方法。

参考文献:

[1]Sahin M A, Leblebicioglu K. A standard expert system for weapon target assignment problem[C] //Proc. of the International Symposium on Performance Evaluation of Computer & Telecommunication Systems, 2009:221-224.

[2]王玮,程树昌,张玉芝.基于遗传算法的一类武器目标分配方法研究[J].系统工程与电子技术,2008, 30( 9) : 1708-1711．

[3]苏淼,钱海,王煦法.基于免疫记忆的蚁群算法的WTA问题求解[J].计算机工程,2008,34(4): 215-217．

[4]高尚,杨静宇.武器-目标分配问题的粒子群优化算法[J].系统工程与电子技术,2005,27(7): 1250-1252．

[5]刘爽英,韩燮.一种求解武器目标分配问题的量子粒子群算法[J].计算机科学,2013,40(2): 235-237.

[6]李欣然,靳雁霞.应用于武器-目标分配问题的量子行为粒子群优化算法[J].计算机应用与软件,2012, 29(12):206-209．

[7]徐克虎,黄大山,王天召.改进的人工免疫算法求解武器目标分配问题[J].系统工程与电子技术,2013, 35(10):2121-2127.

[8] Rashedi E, Nezamabadi H and Saryazdi S. GSA: gravitational search algorithm[J]. Information Science, 2009, 179(13) : 2232-2248．

[9]Kennedy J, Eberhart R. Particle Swarm Optimization [C]//Proc. of IEEE International Conference on Neural Networks. Perth, Australia: [s.n.], 1995.

[10]刘军民,高岳林.混沌粒子群优化算法[J].计算机应用,2008,28(2): 322-325.

*收稿日期:2016-01-17

作者简介:李槟槟(1990—)，男，江西上饶人，硕士研究生，研究方向：目标攻击决策关键技术。E-mail：983692659@qq.com。

中图分类号:TN953

文献标志码:A

文章编号：1008-1194(2016)03-0061-05

WeaponTargetAssignmentMethodBasedonModifiedGravitationSearchAlgorithm

LIBinbin,HEGuangjun,ZHANGMingliang,YOUXiaoliang,TIANDewei

(AirForceEngineeringUniversity,ShaanxiXi’an, 710051)

Abstract:Aimed at the problem of premature convergence in the weapon target assignment (WTA) when using gravitation search algorithm (GSA), a modified GSA was proposed in this paper. Firstly, the abilities to memorize information and share information of particle swarm optimization (PSO) algorithm were introduced into the process of GSA. Then, the operation of chaos search (CS) was also inserted into the improved GSA algorithm, and the modified GSA, named CP-GSA algorithm was proposed. At last, the CP-GSA algorithm was applied directly to solve the WTA minimization problem. The simulation results demonstrated that the proposed method could solve the WTA problem effectively. Specially, to attack eight targets using four air defense units, the proposed method could find the best solution by only 41 iterative operations, and the finest value was 1.18, which was equivalent to that obtained by enumeration method.

Key words:weapon target assignment, gravitation search algorithm, particle swarm optimization, chaos search.