基于灰色关联与量子粒子群寻优的光伏短期预测

贾逸伦，龚庆武，雷杨，林燕贞（武汉大学电气工程学院，湖北武汉　430072）



基于灰色关联与量子粒子群寻优的光伏短期预测

贾逸伦，龚庆武，雷杨，林燕贞
（武汉大学电气工程学院，湖北武汉430072）

摘要：光伏发电系统的功率受天气因素影响很大，结合温度、湿度及辐照强度3个气象因素，对短期光伏功率进行预测。首先阐明3种气象因素与光伏出力的相关关系，进而提出相似日理论，利用灰色关联度分析提取出与预测日气候条件相似的历史日。再将筛选出的历史日数据作为训练数据，利用支持向量机模型对预测日光伏出力进行预测。针对支持向量机中的惩罚系数、不敏感损失系数及核函数核宽度系数的选择，提出改进的量子粒子群算法进行寻优。最后，依据青海某光伏发电站的气候数据及光伏出力数据进行计算，并与带收缩因子的粒子群算法与带惯性权重的粒子群算法进行比较，从误差范围及计算时间等角度，证明了所提方法具有更高的准确性。

关键词：光伏预测；气候条件；灰色关联分析；量子粒子群

Project Supported by National Science and Technology Support Program（2013BAA02B01）.

随着人类对能源的需求逐渐增加，太阳能作为一种重要的可再生能源被广泛关注，光伏发电是利用太阳能的主要方式之一。近年来，光伏发电发展十分迅速[1]，但是光伏发电系统的功率随天气变化而变化，具有不确定性和周期性，大规模的光伏发电并网会对电网造成很大影响[2]。准确预测光伏发电系统的功率对光伏并网系统的安全稳定运行以及大规模发展光伏发电有着重要的意义。

在实际情况中，光伏发电的出力受到多方面因素的影响，主要可概括为两个方面：光伏发电系统部件的性能[3]和气候条件[4]。前者包括装机容量、光伏电池板的材质等，它决定了光伏发电系统自身的发电能力和发电效率，但一般不随时间改变而变化；外界的气候条件包括温度、湿度、气压、风向以及太阳辐照强度等，它是影响光伏发电的随机因素。现今一些专家学者结合上述因素对光伏出力进行预测。文献[5]采用L-M优化算法优化的反向传播算法建立了光伏发电系统出力和太阳辐照强度以及温度的关联模型，再利用神经网络法对光伏电站出力进行短期预测；文献[6]采集和分析了意大利里亚斯特地区的某光伏发电站的温度、太阳辐照强度和发电功率数据，利用2种改进的人工神经网络法对当地的光伏发电站的出力进行预测，得到的预测值与真实值比较接近；文献[7]利用卫星反演的太阳辐射数据来确定云的运动方式，并用以预测太阳能辐照强度，继而预测光伏发电系统的出力。

在上述各方法中，多以太阳辐射为单一变量来预测光伏出力情况，并未考虑温度、湿度及其他影响因素。基于此，本文首先利用灰色关联方法，整体分析各气象因素与光伏出力的相关性，并以此为依据确立相似日，再通过相似日光伏出力数据，利用基于量子粒子群寻优的支持向量机算法进行预测。最后，通过与其他算法所得结果比较，印证本文提出算法可以较好地预测光伏出力，有一定应用价值。

1光伏出力与气候因素间关系

光伏出力与许多气候因素有关，本文采用青海某公司2014年4月光伏出力监测数据和气候条件监测数据进行光伏功率预测，该公司监测的具体气候条件有温度、湿度、日照时长、大气压力、辐照强度等，通过研究观测数据发现，该地4月份每日的大气压力数据基本没有波动，查阅相关文献确认大气压力对光伏发电系统的出力基本没有影响[8]，在整月的监测数据中，每日的日照时长基本一致，而温度、湿度和辐照强度等量随时间变化较大，可能对光伏发电系统出力有影响，故分析这3种气象因素与光伏出力间关系。由于直接的日输出功率与监测到的气象数据不具备可比性，首先对所有功率数据以及气象数据进行归一化处理，再对气象因素和光伏发电系统出力的曲线作直观对比。

光伏发电系统受温度的影响体现在两方面：一是太阳能电池的开路电压、短路电流和峰值功率等受到温度的影响[9]；二是太阳能电池的的转换效率与温度相关。图1显示该发电站某日间隔5 min一次的温度与光伏出力归一化处理之后的相关性关系。由图可以看出，当温度升高时，光伏发电系统的输出功率也随之升高，当温度降低时，光伏发电系统的输出功率也随之降低，但是在时间上存在一定的滞后。

湿度对光伏发电系统的影响主要体现在对太阳辐射情况的影响，相对湿度增加时，空气中的水汽增加，将削弱光伏电池组接收到的太阳辐射强度，从而导致光伏发电系统的出力减弱。图2是湿度与光伏发电系统出力的相关关系，可以看出，当湿度升高时，光伏发电的输出功率降低，当温度降低时，其输出功率升高。两者的变化趋势基本相反。

图1光伏出力与温度相关关系Fig. 1 The correlation of photovoltaic outputpower and temperature

图2光伏出力与湿度相关关系Fig. 2 The correlation of photovoltaic outputpower and humidity

图3是太阳辐照强度与光伏发电系统出力的相关关系，可以看出光伏发电系统的出力与太阳辐照强度的相关度很高，不仅在太阳辐照强度增加或者减少时光伏发电系统出力相应变化，且两者的变化峰值与谷值也基本同时出现，在当日的7:10之前和20:10之后，太阳辐照强度基本为0，此时光伏发电系统的出力也基本为0。

图3光伏出力与辐照强度相关关系Fig. 3 The correlation of photovoltaic output power and irradiation intensity

由以上3图可以判断，太阳辐照强度仍然是光伏发电系统出力的主要影响因素，而温度与湿度也和其有着较强的相关性，故本文从此3方面共同入手，对光伏出力与气候因素进行关联分析，进而进行预测

2相似日理论与灰色关联分析

2.1相似日理论

在电力系统短期负荷预测中，人们发现若预测日在气候、类型上与某一历史日较为相似，预测日与历史日的负荷情况也比较接近，故把气候情况较相似的历史日称作相似日[10-11]。短期光伏发电出力与电力系统负荷预测相同，有着明显的日周期性。统计发现，在2个相似的天气状况下，光伏发电系统的出力曲线相近。因此可基于天气预报信息，选取与预测日天气相似的历史日作为相似日，对预测日的出力进行预测。相似日的选取可由相似度来确定，其表征历史日与预测日气候条件的接近程度，取值在0～1之间，越接近于1则表示2天的气候条件越接近。本文采用灰色关联分析，依据上述3个气候因素确定相似度。

2.2灰色关联度

灰色关联分析是灰色系统理论的一部分，其利用灰关联序来描述各个因素之间的影响程度或者各个因素对于主因素的贡献程度。客观世界中，人们在事物进行系统分析往往很难分清各种影响因素的主次关系以及各自的影响程度，而这恰巧是系统分析的重点与难点。灰色关联分析法是基于灰色系统理论提出来的进行多因素分析的方法，通过序列曲线的几何形状的相似程度来判断各个因素之间联系是否紧密，灰色关联度即各个因素之间的不确定性关联程度或者系统各因子对主因子的不确定性关联程度[12]。

传统的关联度分析通常采用回归分析和相关分析等方法，其都需要较大的样本并且待分析数据之间需要呈典型分布。与以往的数据分析方法不同，灰色关联分析的实质在于比较，而且是整体的、有测度的、有参考系的全面比较，该方法实质是比较各个序列数据所描绘出的曲线的相似程度[13]。常用的灰色关联度模型有邓氏关联度模型、广义关联度模型、灰色斜率关联度模型、欧几里德关联度模型等，本文中采用邓氏关联度模型进行分析，计算公式如下：

设系统的特性行为序列为

系统的相关影响因素行为序列为

若系统满足灰色关联分析四公理，则其邓氏灰色关联系数为

γ（x0（k），xi（k））=

式中：ρ为分辨系数，一般取0.5，相应地，其邓氏灰色关联度为

2.3基于灰色关联分析选取相似日

若n个影响因素的灰色关联度为γ1，γ2，…，γn，则第i项影响因素对于光伏发电功率的影响权重可由式（5）求得：

得到各影响因素对光伏出力的影响权重之后，对第i项因素，可利用式（3）、式（4）求出历史日与预测日的该项影响因素的灰色关联度，可以记为λi（i= 0，1，2，…，n）。逐一求出各项影响因素的灰色关联度，并利用式（6）计算各个历史日对于预测日的相似度值。

利用上述公式计算得到各历史日的相似度值后，按照相似度值从大到小排列，相似度值越大，则该历史日与预测日的光伏出力相关的气候状况越一致。

3基于量子粒子群寻优的支持向量机理论

3.1支持向量机算法

支持向量机方法（SVM）由Corinna Cortes和Vapnik等人在基于统计学理论的VC维和结构风险最小化原理提出[14]。基本思想有二：

1）利用核函数将非线性问题映射到高维线性特征空间中，从而可以利用线性方法对其进行分析。

2）利用结构风险最小化原则构建超平面，更有效、精确地找到全局最优值。

统计数学将回归问题描述为给定的训练样本T={（xi，yi）}，xi∈Rn，yi∈R，寻找Rn空间中的实值函数g（x），使能用决策函数f（x）=sgn（g（x））来推断出与任一输入值x相对应的输出值y。对非线性问题，引入2个松弛变量ξ，ξ*来反映样本点被错误划分的程度，同时引入惩罚系数C作为对错误划分的惩罚，不敏感损失系数ε控制支持向量的数量，并利用映射函数函数φ（x）将非线性问题映射到高维线性空间中去，将其在高维中转化为线性问题[15-16]。引入拉格朗日乘子αi后，其优化及约束函数为

式中：σ为核宽度系数，控制着数据的有效半径。

3.2基于量子粒子群算法寻优的支持向量机

选择合适的核函数后，构造支持向量机模型的关键在于参数的选择，非线性支持向量机模型中惩罚系数C和不敏感损失系数ε控制着模型的复杂程度与精度，对模型的计算时间及所得结果都有重要影响。本文又采用支持向量机核函数，核宽度系数σ的选择也决定了模型的优劣。故需要对（C，σ，ε）三者进行寻优。

许多规范的参数寻优方法被应用于支持向量机的参数寻优中[17]，其中粒子群算法凭借其搜索速度快、效率高、算法简单等优势已被大量应用。而针对其容易陷入早熟收敛和局部收敛的缺陷，一些改进措施被提出应用，其中主要两种为带收缩因子的粒子群算法（YSPSO）与带惯性权重的粒子群算法（SPSO）[18]，且后者的性能通常要优于前者。本文采用量子粒子群改进基本算法，并与前2种算法进行对比

式中，K（xi，xj）=φ（xi）φ（xj）为核函数。核函数定义为非线性映射的内积形式，其有多种选择类型，本文选择应用较为广泛的径向基核函数进行转化，为分析。量子粒子群算法首先由Sun提出，其将粒子群算法理论与量子力学的理论知识相结合，利用量子物理学中的量子运动方式描述粒子的运动，从而保证粒子的运动覆盖整个可行解区域，从而保证搜索到全局最优解[19]。

粒子群算法中粒子运动过程用量子力学来描述时，可以认为粒子群以点qi=（qi，1，qi，2，…，qi，m）为吸引势场中心进行运动。吸引势场中心点的坐标可以描述为

式中：j=0，1，…，m，m为粒子维数；φi，j（t）为[0，1]上均匀分布的随机数；pi，j（t）为粒子经历过的最优位置；pg，j（t）为种群经历过的最优位置。

量子空间中，使用波函数ψ来描述粒子的状态，波函数的模的平方值代表了粒子出现在空间某一点的概率密度，公式为

Q表示粒子在当前时刻在点（x，y，z）出现的概率。假设单个粒子在一维空间中运动时，粒子的位置为X。p是粒子的吸引中心，在多维空间中时即为式（9）中qi，j（t），在p处建立一维δ势阱，通过求解薛定谔方程得到概率密度函数Q，再通过蒙特卡洛随机模拟来测量量子的位置，可得算法的粒子基本进化方程：

式中：L为一维δ势阱的特征长度；u为[0，1]上均匀分布的随机数。在多维空间中的粒子，可对每一维的吸引中心分别建立一维δ势阱进行计算。故求解吸引中心qi，j（t）转化为确定Li，j（t）的值，定义平均最好位置P（t）为粒子群中个体最好位置的平均值，对于m维空间中的n个粒子，平均最好位置为

P（t）=［P1（t），P2（t），…，Pm（t）］=

则Li，j（t）值可由下式确定：

式中：ξ为收缩—扩张系数，也是算法中除了迭代次数和种群规模之外唯一的一个可控制的参数，可以取作一个固定值，也可按一定方式动态变化。带入方程（11），得：

收缩—扩张因子可按式（15）进行变化：

式中：ξmax为收缩—扩张因子最大值；ξmin为最小值；tmax为最大迭代次数。根据如上定义，在粒子群算法中，选定上述参数值后，随机初始化中群内所有粒子位置后，利用式（12）计算种群的平均最优位置P（0），计算每个粒子的适应度值，将当前各粒子的适应度值和当前位置储存于粒子最优解pbest中，当前种群的适应度值和当前最优位置储存于种群最优解gbest中。再用式（9）、式（13）、式（14）更新粒子位置与吸引中心后计算新的各粒子间适应度值，并与之前pbest所保存值相比较，取出更优值。在满足终止条件和最大迭代次数后，输出最优解。

4算例分析

本文利用matlab作为程序开发环境。首先依据青海某光伏发电站2014年4月4日到4月28日25天的监测数据进行相似度分析，取每日有效光照时间为7:10—20:10，将第i日的温度、湿度、太阳辐照强度和光伏发电出力数据序列输入灰色关联分析的matlab程序中，求得其三影响因素对光伏发电出力灰色关联度见表1。由于篇幅有限，本文列出4日、10日、16日、22日与28日数据。

表1每日各项气候条件与光伏发电系统出力的灰色关联度Tab. 1 The grey related degree of each climatic factors and photovoltaic power

取4月4日到4月27日共24日为历史日，4月28日为预测日，将前24日7:10—20:10气候监测数据进行整理，并以4月28日温度、湿度和太阳辐照强度作为参考数据序列，可求得历史日关于预测日各种气象状况的灰色关联度，见表2。

取与预测日气候相似度较高的日期，将其光伏发电数据作为相似日数据进行预测，并应用预测日发电系统出力作为检验。将4月4日至27日共24天的相似度由高到低排列，可得相似度较高的前6天分别为25日、16日、26日、15日、23日和27日，其相似度值见表3和表4。

表2各历史日与预测日各项气候状况的灰色关联度Tab. 2 The grey related degree of the climatic conditionbetween historical day and forecasting day

表3历史日与预测日光伏预测方面相似度Tab. 3 The similarity between historical day and forecasting day

表4相似度较高历史日及相似度值Tab. 4 The similarity value of similar historical days with higher similarity

整理好进行预测的光伏出力数据，便可利用量子粒子群算法寻优的支持向量机法对4月28日7:10—20:10的光伏出力进行预测。以间隔半小时为一点，共预测26个点进行比较。选择粒子群的规模n=20、最大迭代次数tmax=200、取ξmax=1，ξmin=0.5。本文的三参数向量（C，σ，ε），对于空间中第i个粒子，设定为

选取高斯径向基核函数作为支持向量机预测的核函数，以预测数据的平均相对误差作为粒子的适应度值，带入式（9）—式（14）找到最优参数，再将其输入支持向量机中进行预测，得到最终的预测结果。取预测结果与实际结果数据对比，得26个点的预测出力与实际出力如表5所示。

本次预测中，寻优得到的最优参数为C=18.950 7，σ=0.175 9，ε=0.011 5。预测过程耗时t=12.81 s，通过上表可求得预测误差有平均绝对误差MAE= 1.205 MW，平均相对误差MRE=14.15%，均方误差MSE=2.791 MW2，均方根误差RMSE=1.670 7 MW，满足实际工业需求。可以看出，在预测中有少数几个时刻预测误差值较大，是由于该时刻气候条件发生大幅波动。而首尾时刻由于出力基数较小，故相对误差较大。利用QPSO算法寻优的支持向量机预测结果见表5。

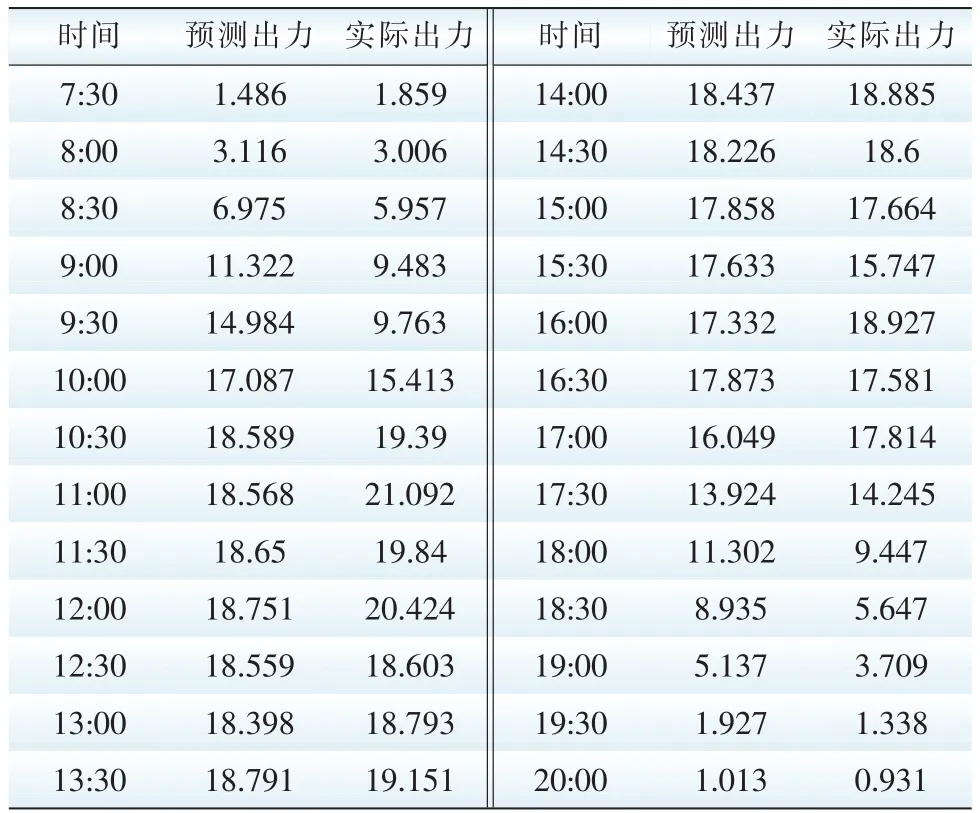
表5利用QPSO算法寻优的支持向量机预测结果Tab. 5 The SVM prediction result using QPSO

再利用带收缩因子的粒子群算法（YSPSO）与带惯性权重的粒子群算法（SPSO），用同样的历史数据对4月28日的光伏出力进行预测。YSPSO算法中，取学习因子c1=c2=2.05，收缩因子ξ=0.73，粒子群规模n=20，最大迭代次数tmax=200，交叉验证折数β=5。此时，寻优参数可得为C=24.484 9，σ=0.398 9，ε= 0.001 6，耗时29.67 s。再利用SPSO算法，取c1=c2=2，最大惯性权重wmax=0.9，最小惯性权重wmin=0.4，粒子群规模n=20，最大迭代次数tmax=200，交叉验证折数β=5。此时寻优参数为C=7.395 1，σ=0.279 0，ε= 0.001 1，耗时41.47 s。3种算法得出的预测结果与实际出力如图4所示。

图4光伏出力实际值与3种方法预测值比较图Fig. 4 The comparison of the actual photovoltaic output power value and the results of three predicting methods

3种算法的计算误差与计算时间比较如表6所示。

表6 3种计算方法误差及用时统计Tab. 6 The calculation error and total time of three predicting methods

从图4及表6可以看出，3种算法的预测精度差别不是十分明显，量子粒子群算法的各项误差略小于另2种算法，说明3种算法都具有一定的应用价值，且QPSO更为精确。在预测实践中，QPSO算法耗时明显优于另2种算法，仅有12.81 s，有着更强的实际应用价值。

由于算法在寻优过程中有一定随机性，为更好考察及比较3种粒子群寻优方法的稳定性与收敛性，本文对其分别进行10次计算，再对预测结果进行比较。分别列出3种算法10次寻优中剔除明显陷入局部收敛结果后平均相对误差最大、最小及用时最快、最慢的4次结果，如表7所示。

表7 3种计算方法10次计算误差及用时统计Tab. 7 The calculation error and total time of threepredicting methods in ten times

可以看出，带收缩因子的粒子群算法所求结果误差范围的波动性较大，平均相对误差波动范围在14.91%至23.01%之间，带惯性权重的粒子群算法的预测结果误差范围波动性相对较小，在14.58%～17.35%之间，但SPSO方法的所用时长要明显大于前2种方法，最高达到85.74 s。经过比较，利用量子粒子群的支持向量机算法所得结果波动性较小，稳定性较高，且精度更强，故有更强的实际应用价值。

5　结论

本文基于相似日理论，采用灰色关联分析进行相似日的选取，提高了预测的准确度，之后介绍了支持向量机算法并引入量子粒子群算法对其进行参数寻优，利用量子粒子群算法寻优的支持向量机算法对光伏发电系统的出力进行预测，通过与其他改进粒子群算法寻优的支持向量机算法比较证明了该方法的良好性能，有效的减小了预测误差。在以下方面，仍可以进行深入研究：

1）本文选取温度、湿度及太阳辐照强度3项指标予以研究，其为影响光伏发电的主要因素，但并不是完全影响因素。今后可研究其他影响因素，并加入相似日的选取过程中。

2）在部分气象数据大幅波动的时刻，光伏的预测值与实际值差距较大，对原始数据进行训练并不能有效地获取数据序列在数量级上的波动信息，故对该点的处理仍可以深入研究。

参考文献

[1] SEMI中国太阳能光伏顾问委员会，中国光伏产业联盟．2013中国光伏产业发展报告[R]．2013.

[2]彭春华，谢鹏，陈臣.大规模光伏电站接入电网可调节鲁棒优化调度[J].中国电机工程学报，2014（25）: 4324-4332. PENG Chunhua，XIE Peng，CHEN Chen. Adjustable robust optimal dispatch of power system with large-scale photovoltaic power stations[J]. Proceedings of the CSEE，2014（25）: 4324-4332（in Chinese）.

[3] FORREST S R. The limits to organic photovoltaic cell efficiency[J]. MRS Bulletin，2005，30（1）: 28-32.

[4]袁晓玲，施俊华，徐杰彦.计及天气类型指数的光伏发电短期出力预测[J].中国电机工程学报，2013（34）: 57-64，12. YUAN Xiaoling，SHI Junhua，XU Jieyan. Short-term power forecasting for photovoltaic generation considering weather typeindex[J]. Proceedings of the CSEE，2013，33 （34）: 57-64（in Chinese）.

[5] ALMONACID F，RUS C，PEREZ P J，et al．Estimation of the energy of a PV generator using artificial neural network[J]．Renewable Energy，2009，34（12）：2743-2750．

[6] ADEL MELLIT，ALESSANDRO MASSI PAVAN．A 24h forecast of solar irradiance using artificial neural network：Application for performance prediction of a grid-connected PV plant at Trieste，Italy[J]．Solar Energy，2010（84）: 807-821．

[7] HAMMER A，HEINEMANN D，HOYER C，et al．Solar energy assessment using remote sensing technologies[J]．Remote Sensing of Environment，2003，86（3）：423-432．

[8] Geoff Stapleton，Susan Neill.太阳能光伏并网发电系统[M].北京：机械工业出版社，2014.

[9]王建军．太阳能光伏发电应用中的温度影响[J]．青海师范大学学报，2005（1）：28-30．WANG Jianjun. The temperature influence on solar PV generation[J]. Journal of Qinghai Normal University（Natural Science Edition），2005（1）: 28-30（in Chinese）.

[10]莫维仁，张伯明，孙宏斌，等.短期负荷预测中选择相似日的探讨[J].清华大学学报：自然科学版，2004（1）: 106-109. MO Weiren，ZHANG Boming，SUN Hongbin，et al. Method to select similar days for short-term load forecasting[J]. Journal-Tsinghua University，2004，44（1）: 106-109（in Chinese）.

[11]李玉娜，马磊，秦光耀.郑州地区太阳辐射变化规律及分析[J].节能技术，2012（5）: 443-446. LI Yuna，MA Lei，QIN Guangyao. The change rule and analysis of sun radiation in Zhengzhou region[J]. Energy Conservation Technology，2012（5）: 443-446（in Chinese）.

[12]李元林，文跃秀，王子力.基于博弈论与灰色关联分析法的城市配电网安全综合评价[J].陕西电力，2013（10）: 5-9. LI Yuanlin，WEN Yuexiu，WANG Zili. City level power grid security comprehensive evaluation based on game theory and grey relational analysis[J]. Shaanxi Electric Power，2013（10）: 5-9（in Chinese）.

[13] WU D. Supplier selection in a fuzzy group setting: A method using grey related analysis and dempster shafer theory[J]. Expert Systems with Applications，2009，36（5）: 8892-8899.

[14] VAPNIK V. The Nature of Statistical Learning Theory[M]. NY: Springer，1995：120-123.

[15]张全明，刘会金.最小二乘支持向量机在电能质量扰动分类中的应用[J].中国电机工程学报，2008（1）: 106-110. ZHANG Quanming，LIU Huijin. Application of LS-SVM in classification of power quality disturbances[J]. Proceedings -Chinese Society of Electrical Engineering，2008，28（1）: 106-110（in Chinese）.

[16]刘英培，栗然，梁海平.基于最小二乘支持向量机优化自抗扰控制器的永磁同步电机直接转矩控制方法[J].中国电机工程学报，2014（27）: 4654-4664. LIU Yingpei，LI Ran，LIANG Haiping. Direct torque control for permanent magnet synchronous motor based on active-disturbance rejection control optimized by least squares support vector machines[J]. Proceedings of the CSEE，2014（27）: 4654-4664（in Chinese）.

[17]龚松建，袁宇浩，王莉，等.基于PSO优化LS-SVM的短期风速预测[J].可再生能源，2011，29（2）: 22-27. GONG Songjian，YUAN Yuhao，WANG Li，et al. Least squares support vector machine optimized by particle swarm optimization algorithm for short-term wind speed forecasting[J]. Renewable Energy Resources，2011（2）: 22-27（in Chinese）.

[18] EBERHART R C，SHI Y．Comparing inertia weights and constriction factors in particle swarm optimization[C]// IEEE Transactions on Evolutionary Computation，Indianapolis，2000：84-88．

[19] SUN J，FENG B，XU W B．Particle swarm optimization with particles having quantum behavior[C]// Proceeding of Congress on Evolutionary Computation，Portland，2004：326-331．

贾逸伦（1991—），男，硕士研究生，研究方向为电力系统负荷与新能源发电预测；

龚庆武（1967—），男，教授，博士生导师，主要从事电力系统继电保护和自动化方面的研究；

雷杨（1988—），男，硕士研究生，研究方向为电力系统运行与控制；

林燕贞（1991—），女，硕士研究生，研究方向为电力系统风险评估。

（编辑徐花荣）

Photovoltaic Power Short-Term Prediction Based on Grey Related Analysis and QPSO-SVM

JIA Yilun，GONG Qingwu，LEI Yang，LIN Yanzhen
（School of Electrical Engineering，Wuhan University，Wuhan 430072，Hubei，China）

ABSTRACT：The climatic factors have great influence on the output power of photovoltaic power system，this article combines three climatic factors-temperature，humidity and irradiation intensity to predict the short -term photovoltaic power. Firstly it illuminates the correlation of photovoltaic output power and these three factors，and then proposes the theory of similar day，which can be extracted by the grey related analysis. Secondly it uses the data of selected similar day as the training data to forecast the photovoltaic output power by support vector machine algorithm. Aiming at choosing the penalty coefficient，insensitive loss coefficient and kernel width coefficient，the article introduces the quantum-behaved particle swarm optimization to optimize. Finally，it uses the climate and photovoltaic output power data of a certain area in Qinghai Province to verify the validity of this algorithm，and compares the result by the method of constriction factors with inertia weights particle swarm optimization. In terms of the error range and computing time，the algorithm proposed by the article can be proved more accurate than the other two methods，and have certain practical value.

KEY WORDS：photovoltaic power prediction；climatic factors；grey related analysis；quantum-behaved particle swarm optimization

作者简介：

收稿日期：2015-08-03。

基金项目：国家科技支撑项目（2013BAA02B01）。

文章编号：1674- 3814（2016）02- 0109- 07

中图分类号：TM73

文献标志码：A