重载列车多目标优化操纵研究

王新培（西南交通大学电气工程学院，成都　611756）



重载列车多目标优化操纵研究

王新培
（西南交通大学电气工程学院，成都611756）

摘要：

关键词：

0　引言

随着世界铁路运输的迅猛发展，高速客运和重载货运成为目前发展的两大方向。按照铁路中长期路网规划，将加快大秦铁路等既有铁路的扩能改造，到2020年我国煤运通道运输能力将达到23亿吨以上。但在重载列车行车过程中，司机只能凭借操纵提示卡信息以及自身积累的行车经验来行车，又因我国客货混跑的现实条件，容易造成司机操纵失误及列车运行安全隐患。如何使得重载列车保证安全的前提下节能平稳运行一直是国内外专家学者非常关心的问题。

在重载列车货运中，降低列车运行能耗有着实际的经济意义。南澳大学SCG研究所在80年代后期已经证明出列车运行在平道或者坡度变化较小的线路上时，理论上存在着最优的操纵序列：“最大牵引—匀速运行—惰行—最大制动”[1-2]。列车在运行过程中必须满足手柄级位切换的规则，牵引工况与制动工况之间的切换必须有惰行工况来过渡，且每种工况必须保持一段时间后才能改变[3-4]。王自力[5-6]总结了列车节能操纵的原则：列车起动和加速过程中，应以最大牵引力加速列车；列车途中运行尽量匀速运行，当匀速运行不能实现时，用锯齿形操纵来逼近匀速；列车在长大下坡道上应采用不断制动、缓解的循环调速制动；列车制动停车时，应以最大制动能力制动停车。由于轮轨黏着的限制、平稳运行的需求，最优控制理论分析得出的结论在工程应用中受到限制，重载列车运行过程呈现多目标性。

重载列车的运行操纵是一个连续的过程，当前运行状态会影响下一状态的操纵，且对未来操纵的影响逐渐减弱。如果选取一定长度的预测区间，进行列车多目标优化，该区间第一步操纵可认为是最优操纵。通过预测区间滚动式的优化过程，得到的操纵序列近似认为是全局最优操纵序列[7-8]。

因此，以列车安全运行、节能运行、操纵平稳、准点到站为运行目标，建立列车运行多目标评价函数，通过各目标不同的权重取值来表征各目标的重要程度，运用矩阵推导和二次规划算法进行数值计算，获得兼顾多个运行目标的列车优化操纵曲线，可为重载列车优化操纵提供一定的理论基础。

1　列车多目标优化操纵模型

1.1模型假设

对列车模型做如下假设：①列车的牵引力和电制动力是连续的，可取其特性外包络线内的任意值，换言之，列车可通过手柄级位平滑调节牵引力和电制动力。②列车空气制动力可发挥的最大减压量为70kP。

1.2模型描述

列车在运行过程中受到各种外力作用，由司机直接操控的有机车牵引力和列车制动力，由各种原因自然发生的统称为列车运行阻力，包括列车基本运行阻力、坡道阻力、曲线阻力和隧道阻力[9]。

引起列车基本运行阻力的因素很多，本文仅考虑列车运行与周围空气发生相对运动产生的摩擦阻力，通常用下式表示[10]：

式中Cx为空气阻力系数；Ω为列车最大截面积，单位为m2；ρ为空气密度，单位为kg/m3；v为列车速度，单位为m/s。

坡道阻力在数值上近似等于坡道千分数：

曲线阻力一般采用综合经验公式计算：

式中R为曲线半径，单位为m；A为用试验方法确定的常数，我国标准轨矩取值为600。

隧道阻力通常采用由实验得出的经验公式计算，由于试验资料较少，本文暂不考虑。

根据牛顿第二定律，列车运动状态方程描述为：

式中m为列车质量，单位为t；F和B分别为列车牵引力和制动力，单位为kN。

预测模型可根据未来的状态确定当前的操纵工况和手柄级位，以Δs为预测步长，N为预测步数，建立目标函数：

式中，P与优化的目标有关，不同的优化目标，P的表达式不同。

1.3多目标评价函数

列车运行优化问题的求解，节能性是备受关注的目标，但对列车优化操纵而言其评价指标一般包含多个。重载列车运行过程中能否安全、节能、操纵平稳、准点到站是评价司机操纵优劣的重要指标。但是各个指标之间有优先级之分，列车安全运行是首要目标，节能运行、操纵平稳是列车优化操纵需要满足的目标，而能否准点到站对于重载列车而言往往受到铁路交通信号的影响。对于各目标的重要性，可用其权重值来体现。因此，离散形式的多目标评价函数J可以写成如下形式[10-11]：

列车牵引能量消耗是直接影响铁路运营成本高低的重要因素，权重w1越大，列车节约的能耗越多，列车在区间内以惰行工况运行的距离越长。列车运行图规定列车在某区段上的运行时间是有限制的，而运行时间与列车在该区段内的目标速度相关，在目标函数中，目标速度vdes越大，权重w2越大，列车的区间运行时间越短。因重载列车载重量大、编组长，其工况不能频繁切换，可通过修改权重w3来调整列车操纵的平稳性。

1.4约束条件

（1）工程投资与结构设计之间的关系。工程设计阶段需要确定材料的选择以及落实工程方案，这与整个建筑工程的投资成本有着重要联系。如果建筑结构设计不合理，建筑工程所需要的建筑材料就会增加，施工难度也会增大，增加施工过程中的人力物力财力损失，最终提高了工程投资。

（1）等式约束

优化区间中列车每步的动能变化受到牵引力、制动力和运行阻力的影响，根据运动学定律描述如下：

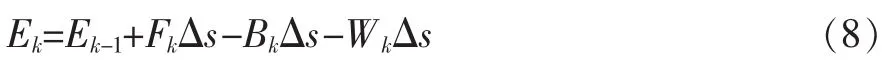
式中，Bk为列车等效制动力，是电制动力和空气制动力之和；Wk为列车运行阻力，是列车在运行过程中受到的坡道阻力、曲线阻力、空气阻力之和：

当k=1时，E0的值与上个优化区间计算出的动能有关：

式中，v0为上一个优化区间计算的列车速度值。

（2）不等式约束

优化区间中列车每步的速度值不能超过当前公里标位置的限速值vlimit，k，本文选取限速值下3km/h作为列车跟随的目标速度vdes，k，用列车动能描述不等式约束如下：

1.5二次规划求解算法

二次规划是指如下形式的优化问题[12]：

把列车动能、牵引力和制动力在优化区间中每步的数值作为矩阵元素：

E=[E1，E2，…，EN]T

F=[F1，F2，…，FN]T

B=[B1，B2，…，BN]T

将这三个矩阵作为优化变量矩阵x的元素：

x=[ET，FT，BT]T

再将多目标评价函数、等式约束条件和不等式约束条件写成二次规划形式进行列车状态的求解，从而得出列车优化操纵曲线。

2　算法结构

编写MATLAB代码对该算法进行仿真实现，该算法主要包括数据输入、仿真计算和数据处理三大模块，算法结构图如图1所示。数据输入模块的功能主要包括列车数据、线路数据（坡道数据和曲线数据）和限速数据的导入，并对数据进行处理；仿真计算模块的功能是对列车优化操纵模型进行二次规划求解，获取列车运行状态；数据处理模块的功能是对仿真计算得出的数据进行处理，包括列车优化操纵曲线、列车牵引力和制动力、线路纵断面图的显示，列车运行数据的Excel导出。

图1　列车优化操纵算法结构图

3　算例仿真

为验证上述算法的有效性，下面针对该算法在既有线上进行列车运行仿真计算，得到列车在该区间运行时每个计算步长的运行状态。本文选取计算步长Δs=50m和计算步数N=30，设置多目标评价函数的权重值为w1=1，w2=10-7，w3=10-5。二次规划算法将对目标函数J中的90个变量在满足30个等式约束和180个不等式约束的条件下进行迭代计算，求得优化变量矩阵。算法中选取第一个步长的计算值，作为该优化区间的最优解。

选取LKJ2000中记录的HXD1型机车运营于大秦线湖东～茶坞这一区间段的数据作为仿真数据。以LKJ2000中记录的限速数据作为限速数据，以湖东～茶坞段的坡道和曲线数据作为线路数据。列车基本参数如表1所示。

表1　列车基本参数

图2为采用列车优化操纵算法计算得到的大秦线湖东～茶坞区段列车优化操纵仿真曲线。图中AB段为列车起车阶段，该区段线路纵断面由一个较缓的下坡道和一个较缓的上坡道组成。列车在该区段运行过程中采用牵引工况使列车加速，处于下坡道时手柄位切换为惰行工况使列车受势能影响行车，处于上坡道时手柄位切换回牵引工况使列车加速运行。BE段为途中调速阶段，该区段纵断面由下坡道组成。其中CD段为长大下坡道区段，BC段和DE段相对于CD段而言坡度变化较小。BC段和DE段中，纵断面较为平缓区段列车使用牵引工况和惰行工况交替运行达到列车调速的目的，有利于列车节能运行；在下坡道区段采用制动工况运行，防止列车速度超过限速，保证列车运行安全；列车牵引工况和制动工况的转换都有惰行工况过渡。由于重载列车轴重大，在长大下坡道区段运行受势能影响列车速度容易超过限速，故CD段列车制动工况和惰行工况交替运行。EF段为列车制动停车阶段，该区段纵断面为下坡道，列车采用最大制动力制动停车。

4　结语

针对重载货运列车区间运行控制的多目标性，建立了基于预测控制的重载列车多目标优化操纵模型，并应用二次规划算法进行求解。通过仿真实例验证，该多目标优化操纵模型，能够满足牵引能耗、速度跟随性和操纵平稳性之间的多目标权衡，符合司机操纵的思想和习惯，满足重载列车优化操纵原则，可为重载列车司机行车提供一定的理论依据

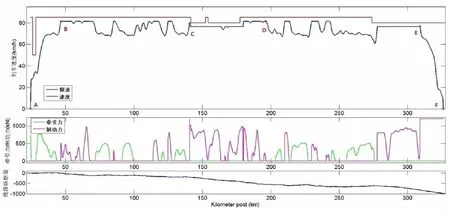
图2　列车优化操纵仿真曲线

参考文献：

[1]Milroy I P.Aspect of Automatic Train Control[D].Doctorial Thesis，Loughborough University，1980.

[2]Lee G H，Milroy I P，Tyler A.Application of Pontryagin's Maximum Principle to the Semi-Automatic Control of Rail Vehicles[C].Proceedings of the 2th Conference on Control Engineering，Newcastle，1982：233-236.

[3]冯晓云.模糊预测控制及其在列车自动驾驶的应用[D].博士学位论文，西南交通大学.2001.

[4]柏赟.内燃牵引货物列车节能操纵模型与实时优化算法[D].博士学位论文.北京交通大学，2010.

[5]王自力.列车操纵优化的离线研究[D].硕士学位论文，西南交通大学，1993.

[6]王自力.列车节能运行优化操纵的研究[J].西南交通大学学报，1994，29（3）：275-280.

[7]李会超，冯晓云，王青元.重载列车优化操纵算法设计与仿真[J].电力机车与城轨车辆，2007，30（6）：40-43.

[8]席裕庚.预测控制[M].北京：国防工业出版社，1993.

[9]张中央.列车牵引计算[M].北京：中国铁道出版社，2010.

[10]Henaler M，Buchholz M，Dietmayer.K.Online Velocity Trajectory Planning for Manual Energy Efficient Driving of Heavy Duty Vehicles Using Model Predictive Control[C].2014 IEEE 17th International Conference on Intelligent Transportation System（ITSC）October 8-11，2014：1814-1819.

[11]李爱娟.智能车辆运动轨迹规划方法的研究[D].博士学位论文，南京航空航天大学，2013.

[12]陈宝林.最优化理论与算法[M].北京：清华大学出版社，2005.

王新培（1991-），女，山东淄博人，硕士研究生，研究方向为列车运行控制技术

Research on Multi-Objective Optimization Strategy of Heavy Haul Train

WANG Xin-pei
（School of Electrical Engineering，Southwest Jiaotong University，Chengdu 611756）

Abstract：

Proposes an algorithm of multi-objective optimization strategy based on predictive model after analyzing the characteristics of heavy haul train operation.The algorithm considers the operation targets of safe，stable，energy saving，on time，and establishes multi-objective evaluation function of heavy haul train based on predictive model.The running state of the train and train optimization strategy running curve can be numerically calculated by using quadratic programming algorithm.In order to verify the validity of the algorithm，Daqin line data is used for simulation calculation.The result shows that multiple targets can be satisfied at the same time and train operation curve meet the optimization strategy principle of heavy haul train.The algorithm can provide certain theoretical basis for the driver driving.

Keywords：

根据电力牵引重载列车的运行特点，对重载列车的优化操纵问题进行分析研究，设计出一种基于预测模型的列车多目标优化操纵算法。该算法综合考虑列车安全、平稳、节能、准点的运行目标，建立基于预测模型的列车多目标评价函数，运用二次规划算法进行数值计算，求得列车的运行状态，得到列车优化操纵运行曲线。采用大秦线数据对算法进行验证，结果表明，该算法可同时满足多个目标，列车运行曲线符合重载列车优化操纵原则，能为司机行车提供一定的理论依据。

重载列车；预测模型；二次规划算法；多目标

文章编号：1007-1423（2016）14-0014-05

DOI：10.3969/j.issn.1007-1423.2016.14.003

作者简介：book=18,ebook=19

收稿日期：2016-03-17修稿日期：2016-04-27

Heavy Haul train；Predictive Model；Quadratic Programming Algorithm；Multi-Objective