电流反馈型 Buck 变换器分岔动力学分析及稳定性控制

李 哲，李颖晖，吴 辰，陈柄任

(空军工程大学航空航天工程学院，陕西 西安 710038)

电流反馈型 Buck 变换器分岔动力学分析及稳定性控制

李 哲，李颖晖，吴 辰，陈柄任

(空军工程大学航空航天工程学院，陕西 西安 710038)

针对电流反馈型 Buck 变换器电路参数波动引起分岔等非线性失稳动力学行为，研究了基于单值矩阵的动力学分析及稳定性控制方法。首先采用菲利波夫法得到了电流反馈型 Buck 变换器的一个线性化的周期轨道，并以单值矩阵的形式来描述。结合 Floquet 理论用单值矩阵的特征值(Floquet 乘子)分析了变换器的稳定性：根据Floquet乘子是否处于单位圆内，判定变换器是否发生分岔失稳。进一步考虑了多参数变化对变换器稳定性的影响，多参数变化条件下系统的稳定域比较狭窄，变换器很容易产生分岔，基于参数共振微扰法，在参考电流中添加小幅周期信号，使变换器模态之间的切换面发生了改变，有效地抑制了变换器的分岔行为，稳定域得到了明显的拓展。仿真和实验验证了该方法和结论的有效性。

Buck 变换器；分岔；菲利波夫法；单值矩阵；稳定性；稳定域

0 引言

在电力系统的实际设计和规划中，稳定运行的参数域一直是工程设计人员十分关注的问题[1-2]。由于分岔[3]与混沌[4]等行为的存在，从动力学的角度分析其稳定性就显得非常重要。电力电子变换器作为电力系统不可或缺的一部分，具有很强的非线性特性。它是一种切换动力学系统，由于开关的存在其被分割为几个线性子模块。对于它的稳定性分析，需要得出其周期轨道的稳定性而不仅仅是计算平衡点的稳定性。因此需要用到一些特殊的方法来获得一个线性化的周期轨道，在以往的研究中，通常是用庞加莱截面来描述整个周期的状态变化，然后在平衡点将其局部线性化，求取雅可比矩阵，通过判断雅可比矩阵的特征值是否处于夫洛开(Floquet)圆内来确定其稳定性[5-6]。遗憾的是，在很多变换器中，并不能得到一个闭合形式的庞加莱曲线，所以这一方法的使用受到了限制。

菲利波夫提出了一种可用于分析不连续系统的数学体系，开始这一方法被广泛应用于机械开关系统，近年研究发现其用于电力电子电路也同样有效[7]。这一方法所得出的单值矩阵与庞加莱截面的雅克比矩阵具有相似的性质。并且当庞加莱截面不能以闭合的形式得出时，这一方法依然有效，且更为直接(庞加莱截面的雅克比矩阵是通过判断受扰轨道的扰动是增强还是减弱来推测轨道稳定性，而单值矩阵的特征值直接与扰动相关)。单值矩阵由各个子系统的状态转移矩阵和用来连接两个子模块的跳跃矩阵组成，而变换器的稳定性正是由状态转移矩阵和跳跃矩阵决定。所以单值矩阵的特征值可以直接指示哪怕是很微弱的扰动下的周期轨道的稳定性[8]。用单值矩阵法来更准确地确定参数的稳定域以及稳定边界有着重要的现实意义。

1 系统模态分析及建模

一般而言，电流反馈型 Buck 变换器的模型如图1 所示当开关 S 和 D 导通或者关断时，系统是不连续的。以时钟脉冲的上升沿为周期起点，S导通，D 关断，电感电流 i上升，此时变换器工作在模态一；当 i上升到时，比较器给触发器一个上升沿触发，S关断，由电感电流 i给负载供电，i减小，D因承受正向电压而导通，此时变换器工作在模态二；若周期时间足够长，那么当 i减小到零时，S和D都关断，由电容给负载供电，此时变换器工作在模态三，直到下一个时钟脉冲的到来。

图1 电流反馈型 Buck 变换器模型Fig. 1 Current mode controlled Buck converter model

分析可知，这是一个典型的切换系统，对于切换系统，通常是建立其基于切换系统的模型，构造Lyapunov 函数分析其稳定性，并以此设计切换控制率。本文采用菲利波夫法在切换点处构造跳跃矩阵，将切换系统转化为一个线性化的周期轨道，用以分析其稳定性，更加形象直观。

表1 变换器数学模型Table 1 Mathematical model of the converter

切换面可分别表示为

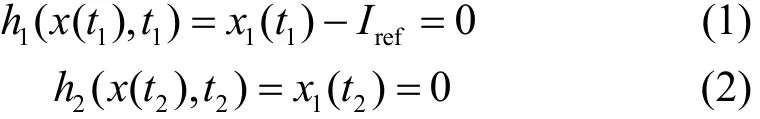
切换面的法向量为

变换器三个模态状态矢量之间的关系为

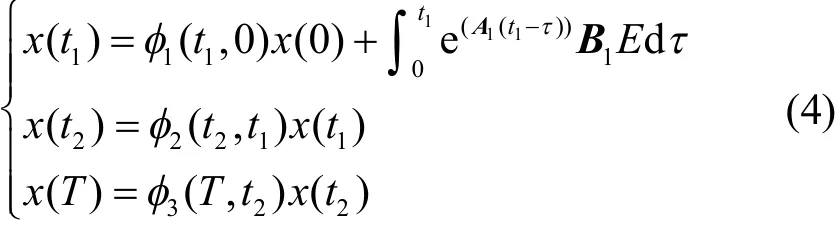
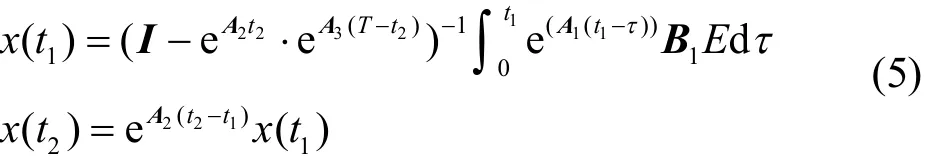
2 单值矩阵的确立

开关从闭合到断开是系统从一个状态到另一个状态的跳跃，且这一过程在很短的时间内完成(几乎无穷小)。可用菲利波夫法来确定跳跃矩阵和单值矩阵。

跳跃矩阵为

单值矩阵由各子系统状态转移矩阵和连接两个子模块的跳跃矩阵组成。电流反馈型 Buck 变换器由三个线性时不变系统组成，取两个切换面的时刻为，则其状态转移矩阵分别为：，

第一个和第二个切换面处的跳跃矩阵可由式(6)求得，而在t= T处还有一个跳跃矩阵，因其为时钟控制，所以跳跃矩阵可视为至此，可以求出整个周期的单值矩阵。

DCM模式下：

CCM模式下：

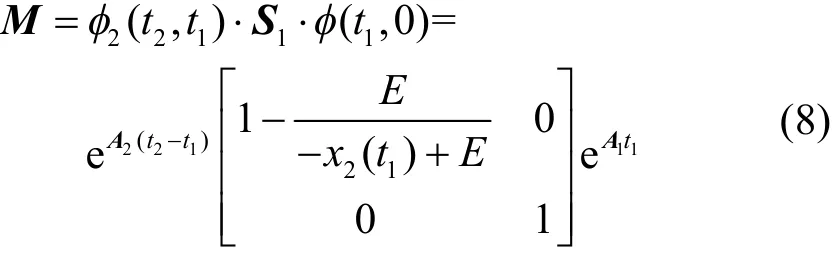
从式(7)、式(8)可以看出，单值矩阵本质上是对一个切换系统围绕其周期轨道的线性化，它的特征值称作 Floquet乘子，根据 Floquet理论，如果 Floquet乘子都处于单位圆内，则认为周期轨道是稳定的。

3 基于单值矩阵的分岔分析

系统初始参数可依表2取值。

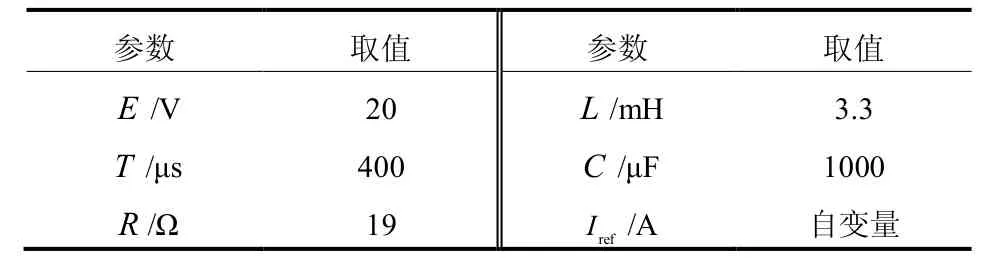
表2 变换器参数Table 2 Parameter values of the converter

一般说来，变换器围绕周期1轨道运行时，将工作在稳定状态。所以预测状态变量的周期1分岔点，显得非常重要。变换器各单元参数如表2所示，利用 Floquet理论，在参考电流变化的情况下，预测变换器的分岔点，如表3所示。

表3 变化对 Floquet乘子的影响Table 3 Floquet multipliers for various inputrefI

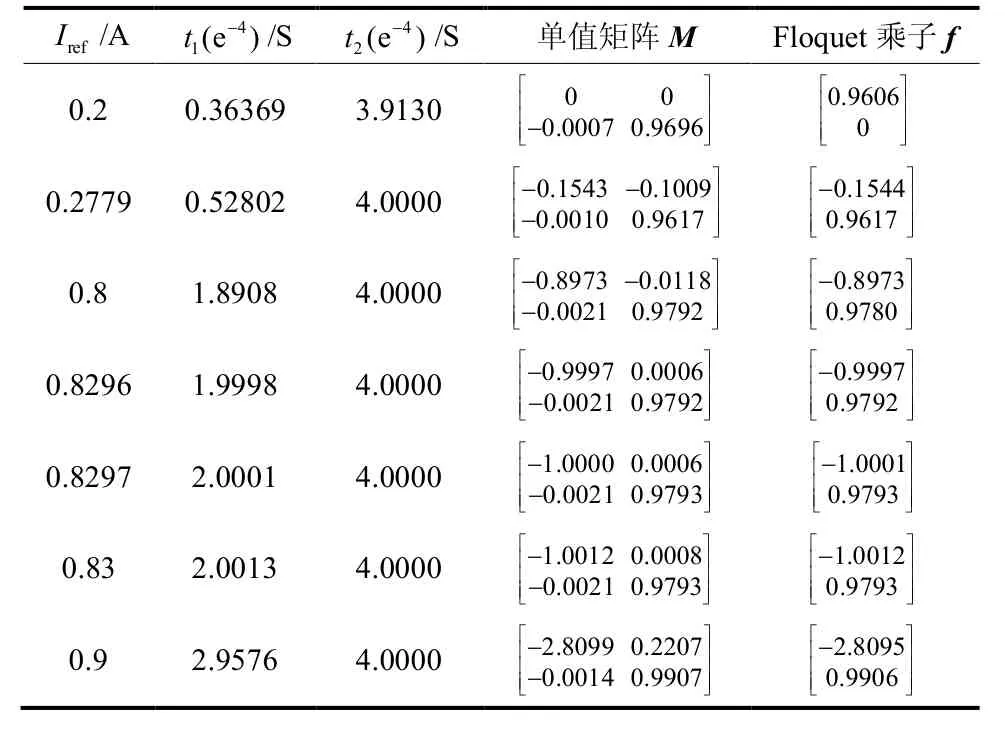
表3 变化对 Floquet乘子的影响Table 3 Floquet multipliers for various inputrefI

I / A 4r e f1( e ) t - / S 42( e ) t - / S 单值矩阵 M F l o q u e t乘子 f 0 . 2 0 . 3 6 3 6 9 3 . 9 1 3 0 0 0 0 . 0 0 0 7 0 . 9 6 9 6éêùêúêúë-úûéùêúêúêúëû0 . 9 6 0 6 0 0 . 2 7 7 9 0 . 5 2 8 0 2 4 . 0 0 0 0 0 . 1 5 4 3 0 . 1 0 0 9 0 . 0 0 1 0 0 . 9 6 1 7éêùéùêúêúêúêúë---úûêë-0 . 1 5 4 4 0 . 9 6 1 7úû0 . 8 1 . 8 9 0 8 4 . 0 0 0 0 0 . 8 9 7 3 0 . 0 1 1 8 0 . 0 0 2 1 0 . 9 7 9 2éêùéùêúêúêúêúë---úûêë-0 . 8 9 7 3 0 . 9 7 8 0úû0 . 8 2 9 6 1 . 9 9 9 8 4 . 0 0 0 0 0 . 9 9 9 7 0 . 0 0 0 6 0 . 0 0 2 1 0 . 9 7 9 2éêùéùê-úêúêúêúë-úûêë-0 . 9 9 9 7 0 . 9 7 9 2úû0 . 8 2 9 7 2 . 0 0 0 1 4 . 0 0 0 0 1 . 0 0 0 0 0 . 0 0 0 6 0 . 0 0 2 1 0 . 9 7 9 3éêùé-1 . 0 0 0 1 0 . 9 7 9 3-úêùêúêúêúë-úûêëúû0 . 8 3 2 . 0 0 1 3 4 . 0 0 0 0 1 . 0 0 1 2 0 . 0 0 0 8 0 . 0 0 2 1 0 . 9 7 9 3éêùéùê-úêúêúêúë-úûêë-1 . 0 0 1 2 0 . 9 7 9 3úû0 . 9 2 . 9 5 7 6 4 . 0 0 0 0 2 . 8 0 9 9 0 . 2 2 0 7 0 . 0 0 1 4 0 . 9 9 0 7éêùéùê-úêúêúêúë-úûêë-2 . 8 0 9 5 0 . 9 9 0 6úû

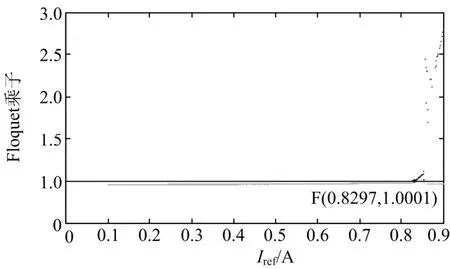
图2 Floquet乘子随参考电流的变化趋势Fig. 2 Values of Floquet multipliers for varyingrefI

图3 以为参数的系统分岔图Fig. 3 Bifurcation diagram of the system for varyingrefI

在实际电路中，变化的参量不止一个，输入电压、参考电压、负载电阻等的小幅变动都是需要考虑的因素，以 Floquet乘子等于-1 为边界条件，可得出在这些参量变化时变换器的稳定区域。图4所示为以参考电流和负载电阻 R 为变量时的变换器周期一轨道的稳定域。

图4 周期 1 轨道稳定域Fig. 4 Stable region of the period-1 orbit

图4 中浅色区域为变换器稳定运行的周期1轨道区域，深色区域为不稳定区域。由此可以看出，参考电流和负载电阻的参数范围非常窄，电路在受到干扰的情况下稍有波动，变换器便可能从稳定转变为不稳定状态。

4 基于参数共振微扰法的稳定性控制

4.1 参数共振微扰法

由式(4)可知，加入正弦信号后，做出改变的只有分母最后一项

则其单值矩阵变为

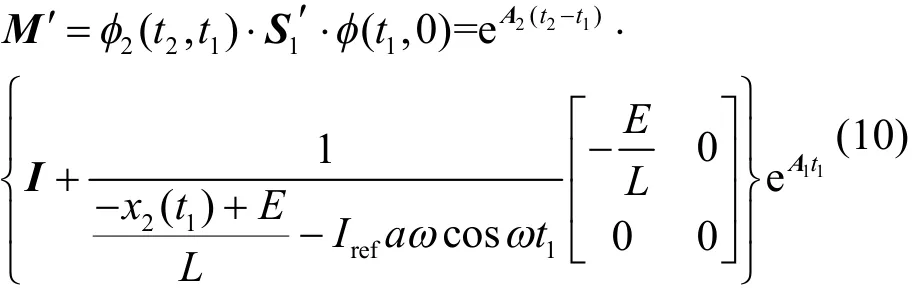
给参考电压加入一个小幅正弦信号之后，从模态一到模态二的切换面发生了改变，如图5所示。

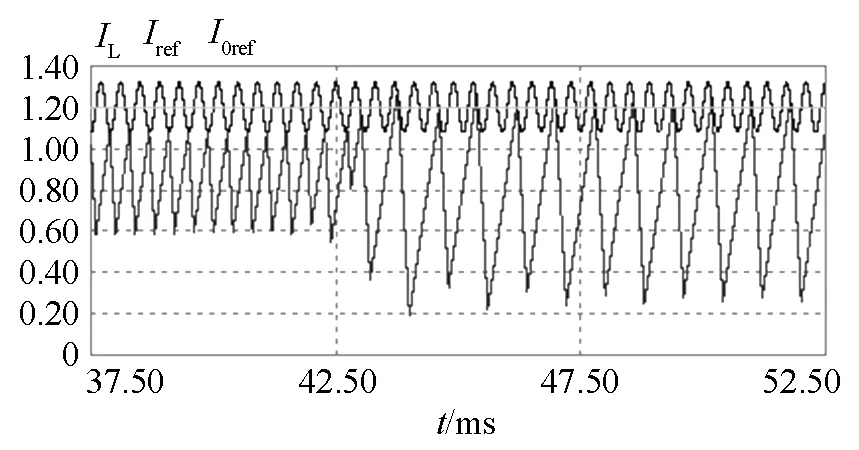
图5 电感电流与切换面原理图Fig. 5 Principle diagram of inductor current and switching hypersurface

由图5 可知，变换器在 t=41 ms 附近开始出现倍周期分岔，但由于小幅正弦信号的加入，电感电流与切换面的交点发生了变化，形成了一个新的切换面，系统在大约经过 14个周期的调整之后，进入了一个新的周期1轨道。这一方法之所以可行，是因为倍周期分岔并没有破坏变换器的周期1轨道，而仅仅是改变了它的稳定性。所以理论上，只要变换器还没有进入混沌状态，通过微小调整切换面，可以使其周期1轨道趋于稳定。

4.2 稳定性控制方法

给参考电流加入小幅正弦信号之后的电路如图6所示。

图6 改善之后的电流反馈型 Buck 变换器Fig. 6 Improved current mode controlled Buck converter

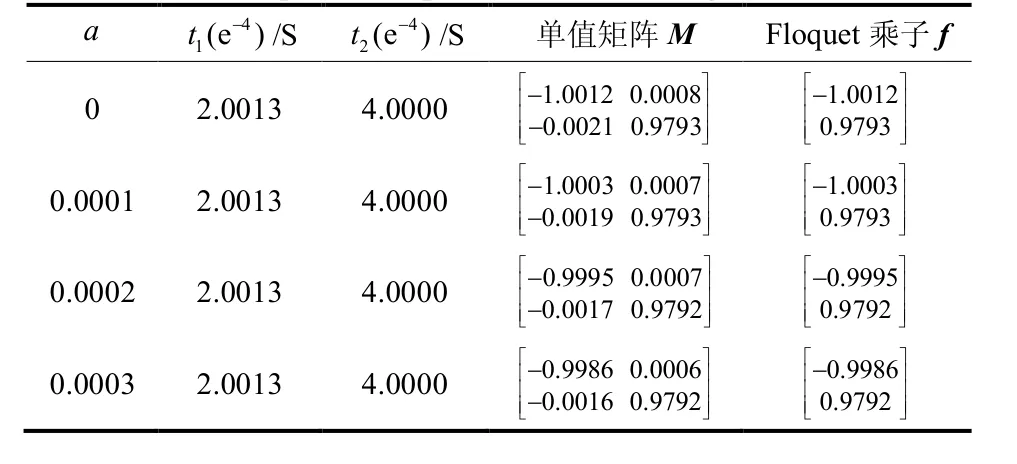
表4 a逐渐增大时的 Floquet乘子Table 4 Floquet multipliers for increasing values of a

由表4可知，一个非常微弱的周期信号的加入，甚至都不能检测到其对开关导通时间 t1所产生的影响，但已足以使原本不稳定的周期1轨道回到稳定状态。而且随着a的增大，变换器的稳定性会变得更好。

图7 电流反馈型 Buck 变换器电感电流波形Fig. 7 Inductor current of current mode controlled Buck converter

图8 电流反馈型 Buck 变换器稳定域Fig. 8 Stable region of current mode controlled Buck converter

通过以上仿真结果可以看出，加入小幅周期信号之后，电路周期1轨道的稳定域得到了明显的拓展。

5 实验验证

根据图1和图6以及本文的电路参数，建立相应的实验平台，其中电源用直流电压源，MOSFET开关管采用 IR2125 驱动，比较器采用 LM311 型集成运算放大器芯片，RS触发器采用或非门构成，时钟脉冲和小幅周期信号由双路输出信号发生器提供，负载电阻采用电子负载。参考电流refI 变化时电感电流的实验时域波形如图9所示。

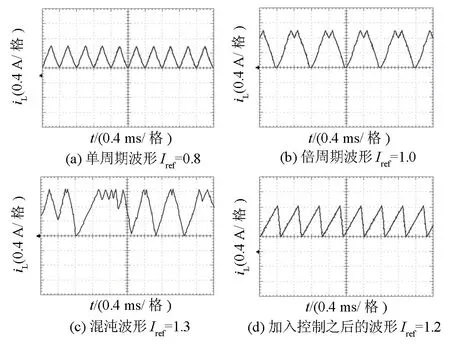
图9 电流反馈型 Buck 变换器实验波形Fig. 9 Experimental waveforms of the current mode controlled Buck converter

实验表明，随着参考电流的增大，电流反馈型Buck 变换器从稳定的周期 1 轨道发生倍周期分岔，最后进入混沌。在变换器未进入混沌之前，通过给参考电流加入一个小幅周期信号，对变换器进行稳定性控制之后，变换器又回到周期1状态，仿真和实验结果验证了本文所提理论的正确性。

6 结论

本文将菲利波夫法应用于电流反馈型 Buck 变换器，分析了变换器在工作过程中可能出现的三个模态，得出了可以指示变换器稳定性的单值矩阵。仿真验证表明，变换器周期一轨道的稳定性与单值矩阵的特征值——Floquet乘子密切相关，在电路参数发生波动时，Floquet乘子的绝对值也会随着增大并最终穿出单位圆，变换器发生倍周期分岔进入不稳定状态。在此基础上得出了在一些可变参量，如参考电压、负载电阻变化时，周期1轨道的稳定域。这一稳定域过于狭窄以至电路参数的选取变得非常苛刻。所以通过给参考电流加入一个小幅周期信号，有效地拓展了变换器电路参数的选取范围，扩大了系统工作的稳定区域。

[1]刘宿城, 周雒维, 卢伟国, 等. 通过小信号环路估计DC-DC 开关变换器的大信号稳定区域预测[J]. 电工技术学报, 2014, 29(4): 63-69. LIU Sucheng, ZHOU Luowei, LU Weiguo, et al. Prediction of large-signal stability region via small-signal loops for DC-DC switching converters[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 63-69.

[2]刘文颖, 徐鹏, 赵子兰, 等. 基于区间估计的风电出力多 场 景 下 静 态 电 压 安 全 域 研 究 [J]. 电 工 技 术 学 报, 2015, 30(3): 172-178. LIU Wenying, XU Peng, ZHAO Zilan, et al. A research of static voltage stability region in wind power scenario based on interval estimation[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 172-178.

[3]邓大上, 房鑫炎. 电压稳定极限曲面法向量在分布式电源选址中的应用 [J]. 电力系统保护 与控制, 2015, 43(5): 57-62. DENG Dashang, FANG Xinyan. Application of normal vector of voltage stability limit surface in distributed generation allocation[J]. Power System Protection and Control, 2015, 43(5): 57-62.

[4]马东娟, 李玲玲. 接触电阻时间序列的混沌特性识别与预测研究[J]. 电力系统保护与控制, 2015, 43(10): 57-61. MA Dongjuan, LI Lingling. Research on chaotic characteristics identification and prediction of contact resistance time series[J]. Power System Protection and Control, 2015, 43(10): 57-61.

[5]王刚, 范学鑫, 付立军, 等. 采用周期轨 Poincaré映射的非线性电力电子系统小干扰稳定性分析[J]. 中国电机工程学报, 2012, 32(1): 84-92. WANG Gang, FAN Xuexin, FU Lijun, et al. Small signal stability analysis of nonlinear power electronic systems based on Poincaré mapping of the periodic orbit[J]. Proceedings of the CSEE, 2012, 32(1): 84-92.

[6]GAVAGSAZ-GHOACHANI R, PHATTANASAK M., MARTIN J, et al. Predicting the onset of bifurcation and stability study of a hybrid current controller for a boost converter[J]. Mathematics and Computers in Simulation, 2013, 91(4): 262-273.

[7]GIAOURIS D, BANERJEE S, ZAHAWI B, et al. Stability analysis of the continuous-conduction-mode buck converter via Filippov’s method[J]. IEEE Transactions on Circuits and Systems, 2008, 55(4): 1084-1096.

[8]AHMET D, KEMAL A. Sensitivity of Schur stability of monodromy matrix[J]. Applied Mathematics and Computation, 2011, 217(15): 6663-6670.

[9]谢帆, 杨汝, 张波. 电流反馈型 Buck 变换器二维分段光滑系统边界碰撞和分岔研究 [J]. 物理学报, 2010, 59(12): 8393-8406. XIE Fan, YANG Ru, ZHANG Bo. Study on border collision and bifurcation of two-dimensional piecewise smooth systems in current mode controlled Buck converter[J]. Chinese Journal of Physics, 2010, 59(12): 8393-8406.

[10]高明远. 双向 DC-DC 变换器基于切换系统的建模与储 能 控 制 [J]. 电 力 系 统 保 护 与 控 制 , 2012, 40(3): 129-134. GAO Mingyuan. Modeling and energy storage control for bi-directional DC-DC converter based on switching system[J]. Power System Protection and Control, 2012, 40(3): 129-134.

[11]HASSAN HOSSEINNIA S, TEJADO I, VINAGRE B. Stability of fractional order switching systems[J]. Computers and Mathematics with Applications, 2013, 66(5): 585-596.

[12]田崇翼 , 李珂 , 张承慧 , 等. 基于切换模型的双 向AC-DC 变 换 器 控制策略 [J]. 电工 技术 学报, 2015, 30(16): 70-76. TIAN Chongyi, LI Ke, ZHANG Chenghui, et al. Control strategy for bi-directional AC-DC converter based on switched system model[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 70-76.

[13]倪福银, 李正明, 潘天红. 光伏微逆变器中 Boost变换器的混沌现象分析与控制研究[J]. 电力系统保护与控制, 2015, 43(17): 149-154. NI Fuyin, LI Zhengming, PAN Tianhong. Analyzation and control research of chaotic phenomena for Boost converter in photovoltaic micro-inverter[J]. Power System Protection and Control, 2015, 43(17): 149-154.

[14]张方樱, 杨汝, 龙晓莉, 等. V2 控制 Buck 变换器分叉与混沌行为的机理及镇定[J]. 物理学报, 2013, 62(21): 84-92.

ZHANG Fangying, YANG Ru, LONG Xiaoli, et al. Mechanism on of instability behaviors and stabilization Y2 controlled buck converter[J]. Chinese Journal of Physics, 2013, 62(21): 84-92.

(编辑 姜新丽)

Study on bifurcation behaviors and stabilization in current mode controlled Buck converter

LI Zhe, LI Yinghui, WU Chen, CHEN Bingren
(School of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi’ an 710038, China)

To restrain the nonlinear dynamical behaviors like bifurcation in current mode controlled Buck converter caused by variation of circuit parameters, a dynamic analysis and control method based on monodromy matrix is studied. First, Filippov’s method is applied to obtain a linearization around the periodic orbit of current mode controlled Buck converter, and it can be described as monodromy matrix; combined with Floquet theory, the eigenvalues of the monodromy matrix (Floquet multipliers) are used to analyze the stability of the converter: the state whether Floquet multipliers are within the unit circle is committed to determine whether the converter occur bifurcation. Meanwhile, the stability of the converter under condition in multi-parameter changes is considered, its stable region is relatively narrow, converter is easy to occur bifurcation and become unstable. Based on the method of resonant parametric perturbation, a slight period signal is added to the reference current, which can change the switching hypersurface between the state of converter, and the bifurcation behaviors can be effectively restrained, through this, stable region is obviously expanded. Finally, the simulation and experimental results show that the analysis method and conclusion proposed is effective.

This work is supported by National Key Basic Research Program of China (973 Program) (No. 2015CB755805).

Buck converter; bifurcation; Filippov’s method; monodromy matrix; stability; stable region

10.7667/PSPC151842

：2015-12-31

李 哲(1992-)，男，通信作者，硕士，研究方向为电力电子与电力传动；E-mail: lizheabcde@163.com

李颖晖(1966-)，女，博士后，教授，博士生导师。研究方向为非线性控制理论；E-mail: liyinghui66@163.com

吴 辰(1988-)，男，博士生，研究方向为先进控制理论。E-mail: chenwukgd@126.com

国家 973 计划(2015CB755805)