关于三角函数与二次函数交汇的值域问题的探究

福建省龙岩市连城一中 张涛生

对于三角函数的性质，包括有界性与单调性问题即-1≤sinx≤1及-1≤cosx≤1,与二次函数交汇，如何解决最值问题？历来都是高中教学的一个难点问题。

一、构建二次函数型的函数，转化为抛物线区间求值的问题

例1.求y = 2 cos2x + 2 sin x -1的最大值？

很多学生认为cos2x 取最大值时y最大，但没考虑此时sinx无法取最大值，怎么办呢？只能综合地考虑，整体化思想，把sinx化为cosx，还是把cos2x 化为sinx呢？显然sinx化为不利，而且还要考虑符号，cos2x = 1- sin2x 更有利，避免麻烦，要注意求sinx的值域。

解：y = 2 (1- s in2x) + 2 sin x -1=-2 sin2x + 2 sin x +1这时利用换元，令sin x=t∈[- 1 ,1]，

∴y = -2t2+ 2 t+1利用配方，

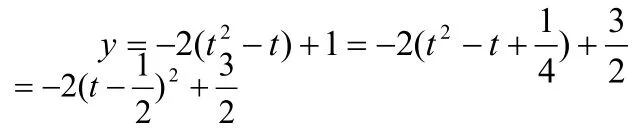
二、对于角度x有限制条件的问题，仍须构建二次函数模型

但要利用t=sinx的单调性来求取值范围,通过对称轴来确定最值。

例2.求的最大值与最小值之和

先转化为y = 1- s in2x + sin x

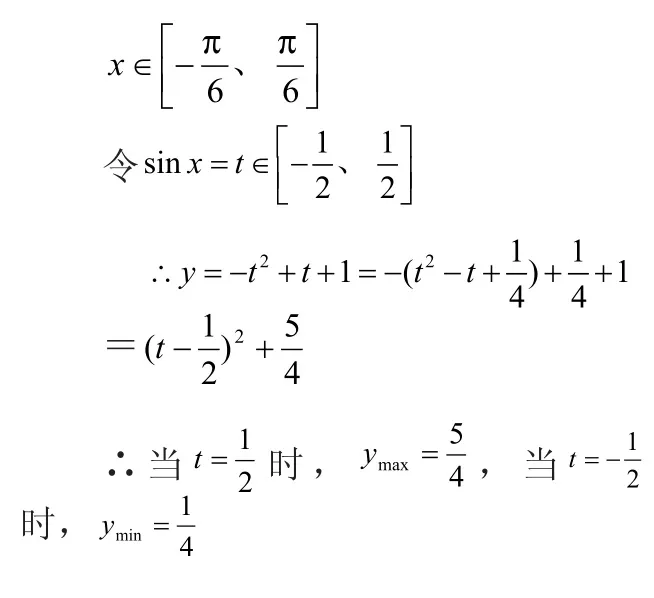
此时要考虑t的范围。

三、内化联系，化归二次函数

例3.求函数y=cosα+ s in α+sinαcosα的最值。

对于学生来讲，该题目可论是未知的，通过转化，将此种未知转化为已知，将原本复杂的问题为学生熟悉，并容易的二次函数问题进行求解。

解：可以引入代换t=cosα + sinα，则

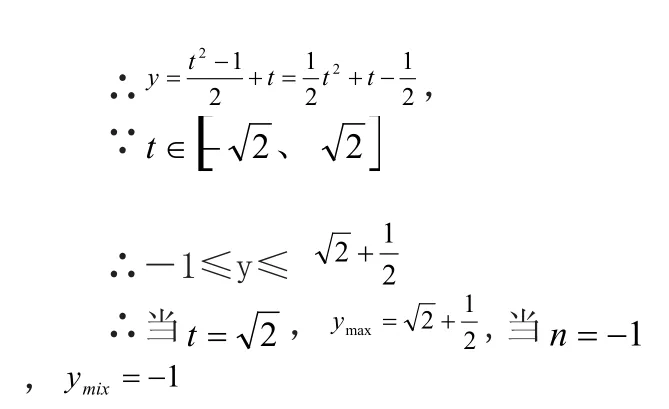
这种将三角函数问题化归为二次函数，可以帮助学生快速对未知问题进行解决，提高学习成绩，建立学习信心。

变式，求函数y =(simx +a)(cosx+a)的最值

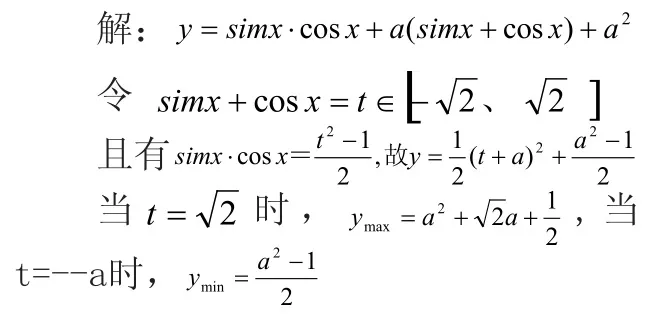
小结，遇到sinx+cosx ，sinx-cosx ，sinx⋅cosx相关的问题，常采用换元法，但要注意范围的确定。通过平方关系知一求二。可以转化为二次函数，由区间端点与对称轴距离来确定最值。

四、含字母参数的二次函数型三角函数问题，按对称轴与区间关系合理分类

挖掘三角函数的有界性问题，结合二次函数的对称性，可以解决最值的问题。

例4．设关于x的函数y = 2 cos2x - 2 a c os x - ( 2 a +1)的最小值为f(a)，试确定满足f( a) =的a值，并对此时的a值求y的最大值．

解：由=及cos x ∈[-1,1]得：

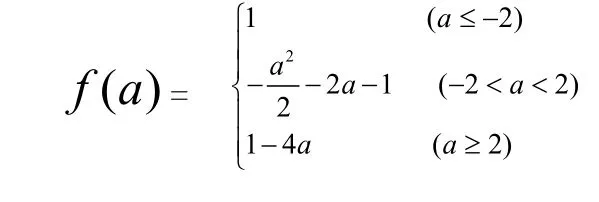
∵,∴当时得，故-,解得：a=－1,此时, 当cosx=1,即x = 2 k π,k ∈ Z 时，ymax=5.

(1)当即－2≤m≤2时，由得函数f(x)的最小值为－4m＋1，由－4m＋1＝19，得

(2)当即m＞2时，由sinx＝－1，得函数f(x)的最小值为得m＝结合m＞2得

(3)当－m2＞1即m＜－2时，由sin x＝1得函数f(x)的最小值为m22－2m＋3，由得m＝－4或m＝8，结合m＜－2得m＝－4.

由(1)、(2)、(3)得m的值为－4或

构建二次函数模型，结合区间与对称轴的关系，通常区间是定的，如果有字母参数，则对称轴是动的，因此分类讨论思想起到引领作用。利用二次函数图象的对称性，有效地确定曲线段，合理确定最高点和最低点，合理解决问题。

因此，解决这类问题基本上先把三角函数换元，转化为二次函数型问题，根据轴与区间的关系。如果含字母参数的，分类讨论为基本框架，就可合理地解决此类问题。