平面内可相交直线序列的遍历算法研究

任　重

（河南检察职业学院，河南　郑州　451191）



平面内可相交直线序列的遍历算法研究

任重

（河南检察职业学院，河南郑州451191）

摘要：平面内可享交直线的算法是几何学中一个经典课题，文章结合国内外的研究现状，提出了几种切实可行的算法，及运用平面内两点和直线的位置关系、两条直线位置关系算法、对称点算法、凸包算法等。同对上述计算方法进行研究和推导，最终得出结论。

关键词：对称点；相交直线；科学算法

自20世纪70年代，由于空间区域研究的需要，几何学诞生。几何学最早是由欧洲数学家欧几里得创造的，几何最早是用来丈量土地。在现代，几何学普遍应用于交通路线图的规划、网络大数据分析、旅行路线安排、GPS导航等领域。通过对大数据信息的分析，算出路程的最短距离，其核心是解ESP问题。

在现实生活当中最短路程问题随处可见，例如，一个学生上课、吃饭再到寝室，需要每天来回重复走到这几个地点，这个学生可以有很多路可选，那么，怎么走那条路路程最近呢？由于这个学生每天都会走，所以他必然懂得走那条路是最近的，然而如果将这三点换成3个国家呢？那恐怕就需要大数据的支持，采用平面内可相交直线序列的算法进行科学的计算，并找出相似的路程方可找到最短距离。

1　国内外研究现状

针对平面图的算法而言，国际上Dijkstra 和Floyd是应用最普遍的两种算法。但是这两种方法也有其自身局限性，就是只能解决点与点之间的最短路线问题。而本文所介绍的ESP问题的算法不局限于点，好包括直线和线段。传统的算法已经不能满足现阶段的计算。

针对简单多边形算法问题，1984年提出Funnel算法，其基本思路是：首先对给定的简单多边形三角剖析，经过计算分析，招到远点P到达Q的对角线，以此找到最短路径。

论文的组织结构

本文根据想要研究的内容，将其分成了6章进行讨论。第一章：研究现状。

这一章主要是对平面内直线能够相交的最近路径进行了讨论，并对其意义和背景进行了阐述，还分析了国内和国外在这个问题上的研究，从而将本文的组织结构以及研究内容引导出来。

第二章：相关基本算法以及基础知识。

这一章主要是在研究中需要通过什么样的基础知识进行了阐述，并讨论了相关的概念，还分析了一些比较经典的算法，给予了可相交直线序列的问题一些理论基础。

第三章：可相交直线序列的遍历以及算法。

这一章主要是对可相交直线序列的最近路线的思路做出了阐述，并对其提出凸多边形的构造，证明了其包含凸多边形的构造，这使得可相交直线的问题有了解决方法。通过这些基础，将几种算法进行对比分析，找出其最短路径的算法。

第四章：算法的设计以及实现。

这一章主要按照实际的操作，给出一些比较详细的算法，通过伪代码描述这些算法，最终将其实现。

第五章：验证算法并分析其结果。

这一章重点对实际运行的结果进行了分析，通过随机的一种序列当做测试数据，利用分析法去验证其求解算法，并给出一定的曲线方程。

第六章：结论。

这一章主要是总结，将文章的结论表明，并描述一些应该加以改进的问题。

2　相关基本算法以及基础知识

2.1计算几何学的概念

在20世纪70年代，就出现了计算几何学，这在计算机科学当中，是非常重要的一个分支，它的起源是根据对算法的分析和设计，在慢慢深入的研究中，其研究成果也慢慢的从最开始的外形发展到了模式识别、统计分析以及地理数据等很多地方。在现如今的大规模集成电路、机器人技术、数学领域以及工程当中，都已经开始广泛使用。

2.2计算几何学的算法简介

针对本文研究的平面可相交序列的遍历算法，在计算几何学中，rubber-band算法与贪婪算法较能针对性的提供计算依据。其他算法如在某些程度上也能为本文研究做出一些贡献。

首先，围绕平面上两条直线的位置关系判定，采用直线斜率的求取，得出两条直线平行或者相交状态。

其次，对于平面点集的凸包的求解，主要有20世纪70年代出现的卷包裹法与graham算法。前者是出现较早的解决凸包问题的基础算法，后者是在平面点集凸包问题上的最优解决算法。在卷包裹的实际演算过程中，在一个点集中取坐标最小的点，即凸包的某个顶点。之后做一条过该点的直线并让直线绕顶点逆时针旋转。

rubber-band算法是俗称的橡皮筋算法，他可以被形象的描述为在起点，和终点相互连接的皮筋。皮筋在绷直状态下就是最短路径。euclidiean最短路径问题的求解的过程中该种算法的应用非常形象直观。Rubber-band算法的具体算法流程以程序判断图示意为：开始→初始路径的长度计算→专门针对路径点集合进行处理→得出处理结果后，计算两次路径长度之差并与精度标准对比→如果求差结果大于精度则重新开始路径点集合的处理步骤。反之基于整个路径点得出最短路径。

贪婪算法被称为登山法，其进行原理一般如同登山一样的步步为营。逐步的将全局的问题转化为小部分的问题，并保证局部实现最优化解决方案，当一部分出现无解或者不能进行时，全部算法过程就会停止。其特点就是简单。便捷。并能同时进行。贪婪算法在求解某些问题上具有自身的优越性，诸如拓扑排序问题，背包问题以及本文中多次涉及到的路径最短问题。

3　可相交直线序列的遍历以及算法

平面内可相交直线序列的遍历算法研究三、平面内可相交直线序列的遍历及求解算法平面内可相交直线序列的遍历已经受到国内外几何领域学者的广泛关注。目前，学者对于平面内可相交直线序列的遍历的算法的研究非常的少。笔者就在目前几何领域的研究成果上，分析平面内可相交直线序列的遍历的几何特征，将其转换成可相交线段的问题并通过其算法，来研究平面内可相交直线序列的遍历的求解算法。（1）总体思路对于平面内可相交直线序列的遍历问题，首先，笔者根据直线的起点和终点的相交来获得一个凸多边形，其次，遍历途径必定包含在直线构造的凸多边形中，因此，笔者将平面内可相交直线序列的遍历的问题转换成多边形内可相交线段的遍历的问题。最后，笔者通过对Rubberband算法的研究来解决平面内可相交直线序列的遍历的问题。（2）凸多边形F的构造。如图1所示，如果图中的虚线部分是一条遍历途径，虚线在凸包边缘的内部并且凸包的边缘和所有的遍历直线相交，那么这条虚线所代表的遍历途径将不是最短的直线。因此，如果直线的起点和终点相同，那么计算出的便是一个凸多边形。反之，则不是。（3）多边形内相交线段的遍历问题在多边形内相交线段的遍历的算法中，Rubber-band算法是其中最经典的算法之一。Rubber-band算法是从局部最优达到全局最优。在Rubber-band算法的算法中，主要是通过最短路径差来考虑下一步的进行。当线段存在相交时，Rubber-band算法则会出现退化的现象。如图2所示。在Rubber-band算法的过程中，当两条线段相同时，下一步的进行就会停止不动，导致Rubber-band算法提前结束，这将使算法得不到正确的答案。

因此，交换线段顺序的算法能够更好的求解平面内可相交直线序列的遍历问题。

4　算法设计与实现

4.1算法流程

在分析平面内可相交直线序列的遍历算法流程时，可以将其分为求凸包和求多边形，以及用改进Rubber-band算法求最短遍历路径这几个步骤。其中在求凸包的步骤中，主要采用的是Graham算法来进行相应点集的计算。而在求多边形的过程中，则需要现根据已经计算出的凸包切线，通过对顶点处的切线进行构建，建立包含这些凸包的多边形。构建处的多边形如图3所示。

图1　凸多边形F的构造

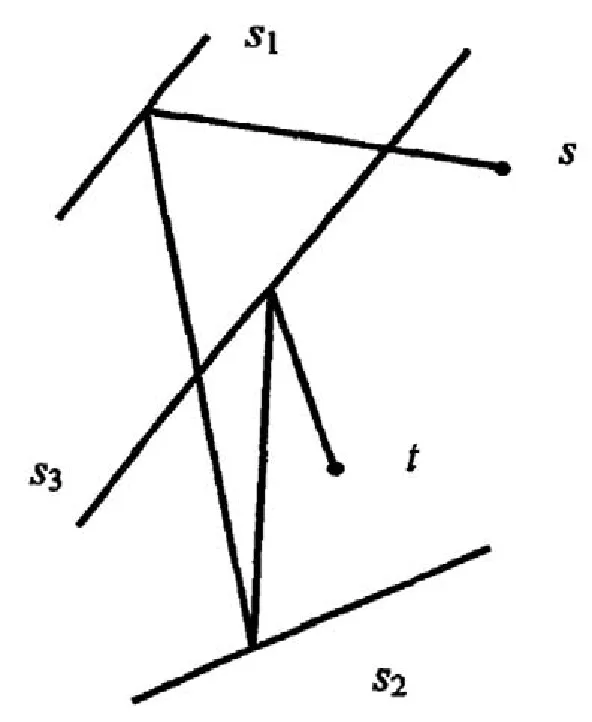
图2　凸多边形F的构造

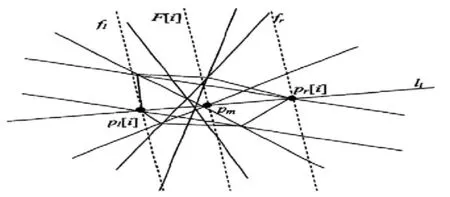
图3　构建处的多边形

最后是用改进Rubber-band算法求最短遍历路径，就是依靠算法的基本思想和理念，设计出更加高效科学的便利算法，以提高对平面内可相交直线的算法。

4.2基本数据结构

在进行平面内相交直线的算法中，基本的数据结构其实就是点线面这三种类型。其中点是最常见的基本类型，也是最基础的数据结构组成部分。而直线则是关系算法研究的重要部分，既可以用ax+by+c=o的方式进行表现，也可以通过y=k*（x-pt.x）+py.t的结构来表示，除此之外在遍历算法中还有依靠判断直线是否属于相等函数的算法。

4.3算法实现

算法实现指的就是对平面内可相交直线序列算法的实现过程，最主要的就是主流算法的计算过程，如图4所示。

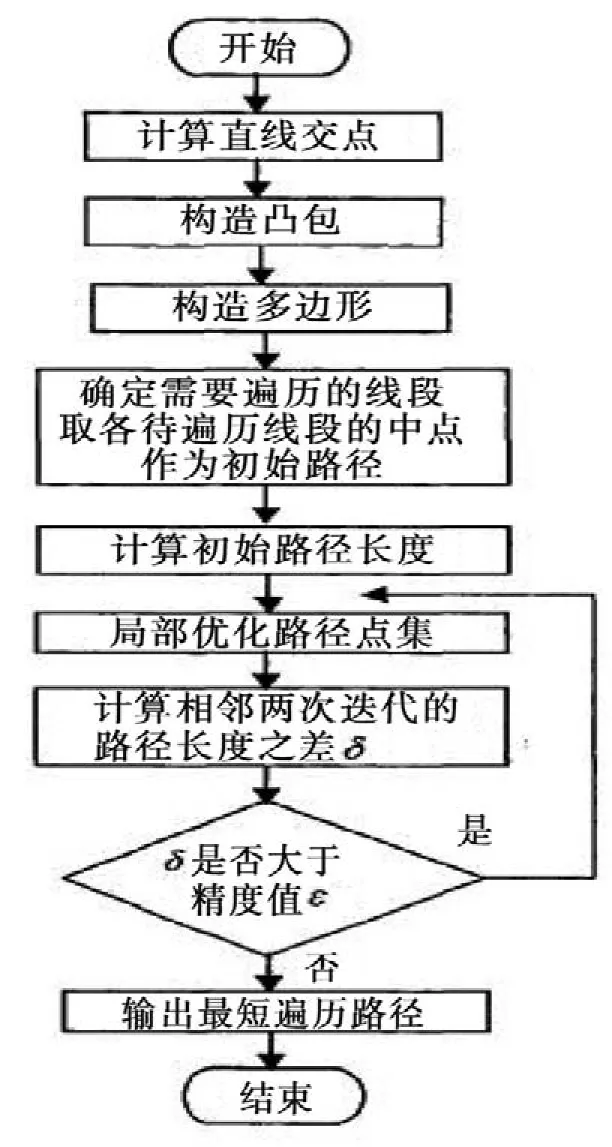
图4　主流算法的计算过程

5　算法验证及结果分析

算法验证和结果分析，主要针对的就是对分析验算的结果继续测试和分析，通过使用事后分析法，对算法的有效性进行科学的验证，其中可以分为测试数据生成和运行结果分析两部分。

测试数据生成就是为了验证算法的正确性，可以借助随机生成的大量数据进行验证，并对计算的结果进行分析，通过对数据的VC++实现处理，对遍历算法的各个步骤进行详细的结构分析，通过将其同理论数据相比较，进而验证算法的正确性和时间复杂度，进一步加强对平面内可相交直线序列的便利算法研究。

6　对未来遍历算法的预测

上文已经细致研究了平面内相交直线序列存在的遍历算法，同时也探索出了另一种改进Rubber-band算法的思路，实现平面内相交直线序列的遍历算法，以及求解出其遍历问题，这也是该文研究成果精髓所在。可是，由于本文实际的内容还不够完善，致使在研究方面所涉及的相关内容还存在一些小的缺陷，这些曲线对遍历算法未来的发展还存在一定的影响，因此，对对未来遍历算法的预测，可以从以下几个方面问题难点着手。

（1）本文虽提出的算法因其条件的限制，还只适用于对两条直线相交于一点的情况进行分析、求解及处理，而涉及3条或3条以上的直线相交同一点的情况，因为还没有对其做针对性的研究，该算法是否适用将无从得知，这也使得该问题成为遍历算法未来要攻克的一个方面。

（2）本位只涉及了构造多边形算法中的部分方式进行了运用，而对更复杂、更优化的时间算法还没有涉及到，因此在未来遍历算法的研究中，可以运用此算法，从而减少算法的整体执行时间，实现高效的遍历算法。

7　结语

本文对平面内可相交直线序列中存在的遍历问题进行了较为深切的分析和研究，讨论了最短路径的求解方式在几何学计算中的有关基础理论知识，研究了直线之间存在的位置关系，并例举出以构造多边形的方式，对直线的初始访问顺序进行确认与肯定。同时将构造多边形的内部添加进最短遍历路径，实现了构造多边形内部相交线段的遍历算法，也对其进行了相当深入的对比与研究。而从遍历算法的几种不同性质的线段中，对其思路的改进也使得Rubber-band的运用适应了可相交直线序列，其共同作用使可相交直线序列的遍历算法最终得以实现及证明。此外构造测试数据，证明了在实际运行中其设计的算法所得出运行结果的准确性。

［参考文献］

［1］谭锦彪.遍历平面内Partial-Order线段集的ESP求解算法研究［D］.大连：大连海事大学，2013.

［2］郑毅.访问平面内线段序列的ESP问题求解算法研究［D］.大连：大连海事大学，2012.

［3］孙立晓.访问平面内不相交线段的ESP问题求解算法研究［D］.大连：大连海事大学，2012.

［4］兰明.平面内经过若干不相交线段的L1问题求解研究［D］.大连：大连海事大学，2011.

［5］徐丽丽.基于flip的Delaunay三角剖分算法研究［D］.大连：大连海事大学，2010.

［6］任保营.基于Delaunay三角剖分的TSP问题求解研究［D］.大连：大连海事大学，2010.

［7］侯斌.简单多边形内Euclidean最短路径问题算法研究［D］.大连：大连海事大学，2010.

［8］邓礼礼.求图中受限制的所有最短路径算法的分析与研究［D］.上海：华东师范大学，2009.

Research on the Traversal Algorithm of Intersecting Lines in Plane

Ren Zhong
(Henan Procuratorial Vocational College, Zhengzhou451191, China)

Abstract：Plane eligible AC linear algorithm is a classical topic in geometry, this paper research status at home and abroad, and puts forward several feasible algorithm and using plane two points and a straight line position, two linear position relation algorithm, symmetric algorithm， convex hull algorithm. The calculation method is studied and deduced， and fnally the conclusion is drawn.

Key words：symmetry point； intersection line； scientifc algorithm

作者简介：任重（1981-），男，河南郑州，本科；研究方向：算法设计和分析。