教学中旋转矢量法的应用
——以简谐振动为例
陈 新,王 赵,唐 敏
(海南大学 材料与化工学院,海南 海口570228)
教学中旋转矢量法的应用
——以简谐振动为例
陈新,王赵,唐敏
(海南大学 材料与化工学院,海南 海口570228)
摘要:高等院校工科学生在大学物理和电工学学习中的一个难点:旋转矢量法,阐明了旋转矢量法与简谐振动各物理量的对应关系,还通过运用旋转矢量法处理简谐振动中一些具体问题,旋转矢量法在实际解题中灵活运用, 可将一些复杂分析和运算转化为简单的几何运算,有助于简化在简谐振动研究中的数学处理,使各物理量之间关系更清晰、具体、直观、形象地呈现在学生面前,帮助其熟练掌握“简谐振动”等有关概念和规律,提高解决有关问题效率。
关键词:旋转矢量;简谐振动;相位;初相
引言
作为自然科学基础学科之一,大学物理是研究客观物质世界基本运动规律的科学,是基于工程实践教学和工程技术的支柱学科之一,是高等院校理工科学生的必修课。
振动是物质基本运动形式,是物理学中常见现象,而简谐振动是机械振动中最基本最简单振动,任何一个复杂振动都可以看成是若干个谐振动的合成[1][2][3]。谐振动的基本物理量有三个:振幅A、周期T/角频率ω、相位φ/初相φ0,其中A由初始条件决定,T/ω由振动系统本身的性质决定,均比较容易求出,而难点是φ/φ0的求解。简谐振动和交流电相位和初相位两个物理量对理解相关概念和规律有很大帮助,在大学物理和电工学教学中,对于简谐振动和交流电教学重点主要是掌握上述两个基本物理量,这也是考查重点。
一般来讲,可通过两种方法来求解简谐振动方程相位;解析法和旋转矢量法。对大部分学生来说,相对于新知识——旋转矢量法,他们倾向于用高中熟悉的解析法——多个方程联立求解。但是解析法面对三角函数,必然要面对多值选择问题,许多同学通常在这个问题上犯错误。
相比于解析法,旋转矢量法是研究谐振动的更为简便、更有效的几何方法,它的实质就是把周期性的简谐振动与我们非常熟悉的匀速圆周运动有机结合起来,避免多值选择的困难。本文将在简要介绍旋转矢量法的基础上,重点介绍该法在求解简谐振动的一些具体问题中的应用技巧。
我们首先来看看旋转矢量与矢量图。
一、旋转矢量与矢量图
用旋转矢量表示谐振动的图称为旋转矢量图(如图1),把这种描述简谐振动的方法称为“旋转矢量法”。由于矢量图直观形象、清晰明了,富有启发性,且应用十分灵活,所以在教学中有着相当重要地位。对于旋转矢量图,首先要明确它与简谐振动各物理量的对应关系,这样才能在旋转矢量法中熟练运用[4]。

图1 谐振动的旋转矢量图

4.矢量旋转所围绕的点O即圆心是坐标原点,又是简谐振动的平衡位置;
5.圆上某点绕逆时针的切线方向为该点的速度方向,从图1可以看到,上半圆圆周上各点的速度在X轴上投影为负,而下半圆圆周上各点的速度在X轴上投影为正(相比较于OX轴正方向)。
前三者是决定谐振动的基本物理量,教材和文献中讲的较多,后面两点则少有专门论述,其实这两点对于理解旋转矢量法的物理意义是很重要的,尤其是第5点在用旋转矢量法解题时的应用至为关键。
可见,用旋转矢量图可以把简谐振动的特征量(如相位)形象反映出来。
二、利用旋转矢量法解决简谐振动问题的基本步骤
1.根据观察点的位移正负在旋转矢量图中找到位移对应的一个或两个位置;
2.根据观察点的速度方向,结合前面内容一中的第5点,在1中寻找唯一正确的位置;
3.根据2中找到的位置和题目其他条件进行问题求解。
三、实例运用
下面我们通过一些示例来实践一下。
(一)对比旋转矢量法和解析法,确定相位和初相位
前述,在振幅A,角速度ω已确定情况下,由式1可知,简谐振动方程可以由相位ωt+φ0决定。在一次全振动过程中,每一时刻的运动状态都不相同,而这种不同就反映在位相的不同上。这表明,相位φ是确定质点振动状态(位移、速度)的关键物理量φ0,φ0而t=0确定相位首先要确定初相位。是t=0时的相位,其数值由初始条件决定,它决定物体起始时刻的振动状态〔2, 4, 6〕。
由于振动方程1中,cos为偶函数,因此±(ωt+φ0)都能使方程成立。究竟选取正值还是负值,一般是根据某一时刻物体的运动方向,即速度(v=-Aωsin(ωt+φ0)))的方向来帮助确定相位。

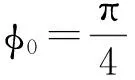
但是用解析法解题,如对三角函数不熟悉,往往容易造成错误。而借助于旋转矢量图问题会变得直观、清晰,如例2,可以方便地解决相位不定问题。


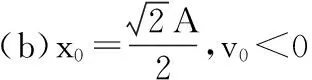


图2t=0时各位置的旋转矢量图
解:根据题意,做出矢量图2-(a)-(d),由旋转矢量法可知:
(1) t=0时,旋转矢量端点在X轴上投影在A,由于该点对应只有一个点,没有多值问题,φ0=0(见图2-(a),类似的有x0=-A这个点,x0=π,或-π),x=Acos(ωt);

由上解题过程中可以发现,相位、初相与振动质点的振动状态一一对应,一目了然,十分形象。
(二)比较相位关系
要利用旋转矢量法,先根据振动图形判断质点的振动速度方向,法则如下:在振动图形中,观察点的下一个点在观察点上面,速度为正;观察点的下一个点在观察点下面,速度为负。
例3,有两个同频率的谐振动的x—t曲线。如图3(a)所示,求两者的相位差。

图3 (a) x—t曲线 图3 (b)两谐振动在t=0时的旋转矢量图

(三)求运动的时间间隔Δt
简谐振子的运动是变速直线运动,而旋转矢量的转动是匀速率的,所以利用旋转矢量法在求解简谐振动的某些问题,如振动时间及质点运动的时间间隔等的计算得以简化,学生更容易接受[4-7]。

解:根据题意,ω=π,旋转矢量如图所示。


结论
综上所示,旋转矢量作为描述简谐振动的一种方法,灵活运用它,可将一些复杂分析和运算转化为简单的几何运算,有助于简化在简谐振动研究中的数学处理,使各物理量之间关系能更清晰、具体、直观、形象地呈现在学生面前,帮助他们熟练掌握“简谐振动”等有关概念和规律,提高解决有关问题的效率。
教学中,我们不但要注意简谐振动基本理论讲述,还要加强学生用矢量图解题的强化训练,使学生在掌握基本概念的同时能熟练利用旋转矢量法对谐振动进行分析和运算,从而取得比较好的教学效果。
参考文献:
[1]张三惠.大学物理学(第3版)[M].北京:清华大学出版社,2000.
[2]张文杰,曹阳主.大学物理教程(第1版)[M].北京:中国农业大学出版社,2009.
[3]程守洙,江之永.普通物理学(1)[M].北京:高等教育出版社,1982.
[4]徐纯辉.旋转矢量法的问题归类教学法[J].高等函授学报(自然科学版),2007 (1).
[5]刘新.旋转矢量法确定相位不定问题[J].江苏农学院学报,1998(4).
[6]管永精,王慧娟,冯禄燕.利用旋转矢量法求解简谐振动中的位相[J].广西大学学报(自然科学版),2009(Z1).
[7]朱青.旋转矢量法在“简谐振动”教学中的应用[J].中山大学学报论丛,2006(1).
(责任编辑:赵峰)
Application of Rotation Vector on Teaching of Harmonic Vibration ——Taking Simple Harmonic Vibration as an Example
CHEN Xin,WANG Zhao,TANG Min
(School of Material and Chemical Engineering, Hainan University, Haikou 570228, China)
Abstract:Initial phase angle is the most difficult to be obtained among three characteristic scalars in Harmonic Motion.We approach the initial phase angle by the analytical method,revolving vector method,and analysis & revolving vector method.Then we offered some convenient and fast methods to determine the initial phase angle.
Key words:rotation vector;harmonic vibration;phase;initial phase;
收稿日期:2015-12-29
作者简介:陈新,男,汉族,四川成都人。工学硕士。海南大学材料与化工学院讲师。主要研究方向:高校实践教学、生物物理统计;王赵,男,汉族,海南海口人。理学博士。海南大学材料与化工学院副教授。主要研究方向:原子、分子物理;通讯作者:唐敏,女,汉族,河南滑县人。理学博士。海南大学材料与化工学院副教授。主要研究方向:高校实践教学、水生生物。
基金项目:2012年海南大学教育教学研究项目“材料科学与工程专业“卓越工程师培养计划”教学模式初步探讨“(编号:hdjy1208)成果之一;2013年海南省高等学校科学研究项目“材料科学与工程专业‘卓越工程师培养计划’教学模式初步探讨”(编号:hjjg2013-05)成果之一。
中图分类号:O411
文献标识码:A
文章编号:1009-9743(2016)01-0116-05
DOI:10.13803/j.cnki.issn1009-9743.2016.01.024

