发展学生运算能力应当“法理并重”

◇潘可可 唐彩斌

发展学生运算能力应当“法理并重”

◇潘可可 唐彩斌

运算能力在《数学课程标准（2011）》中被作为核心概念重提，再次受到大家的广泛关注。当然重提并不意味着回到从前，不应该被解读为 “重新恢复那些复杂烦琐的计算，追求高速度、高效率的计算”（刘坚，2012）。会算法、懂算理，是运算能力的两个重要组成部分，所以当前培养学生的运算能力应当“法理并重”。

笔者在2014年从四年级的2500多名学生中随机选取300名，作“除数是两位数的除法”计算能力的测查。A卷主要是考查学生对计算方法的掌握情况，有92÷30、196÷39、288÷32、134÷ 26、945÷45等14道不同类型的算式题；B卷则主要是考查学生对算理的理解情况，题如：怎么计算945÷32？写下你的思考过程。测试结果是，A卷的正确率高达99%，而B卷的正确率只有20%。“会算法不会说算理或者说不好算理”的现象比比皆是。从归因来看，除这两种能力本身不在同一思维水平，因此学生掌握情况有差异外，也反映出我们平时的计算教学的确“重算法轻算理”。本文试图罗列不同数域中一些典型的算理，以此来强调，在小学数学教学中，要让学生会“算术”更会讲“算理”，通过“讲理”进一步提升学生的运算能力。

一 不同数域运算能力中需要说明的若干“算理”

1.整数四则运算的顺序，为什么有时从低位算起，有时又从高位算起？

从数学史中可以发现，在笔算形成的初期，加、减、乘、除都是从高位算起的，只是在笔算加法、减法和乘法遇到进位时，需要改写前面的数字，才逐步改为从低位算起。12世纪印度沙盘上的数学就是如此。（如图1）

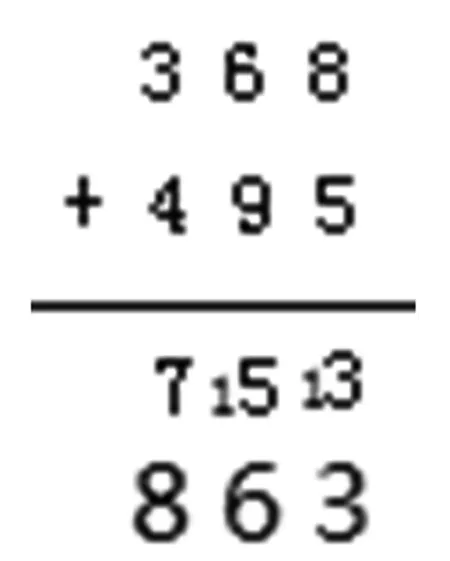
图1

因此在课堂教学中，学生顺着从高位到低位的思路进行计算是完全可以理解的，只有让学生经历从高位算起，感受到因低位的进位要调整高位上的数而带来的麻烦时，他们才会得到从低位算起比较方便的深切体验，而不需要强制加以“规定”，这样的“法”才是“理”之下学生愿意接受的。（当然，如果学生能够把高位的计算结果暂时记在脑子里，然后根据低位的计算结果来确定，那么从高位算起也是可以的。就像在口算中所倡导的从高位算起那样）

整数的加、减、乘三种运算在列竖式计算时，一般都从低位算起，偏偏除法特殊，除法竖式的格式本身也和其他三种运算不一致，这些外形的不同都源自除法本身的意义和竖式的要求。如果我们把乘法定义为连加，那么除法就是连减了。竖式计算的实质是，将当前对于两个数的计算归结为它们各个数位上数的计算，以求出得数的各个数位上的数。（如图2）要把计算的中间过程与最后的结果都记录下来，除法的竖式发展到今天就是从高位算起了。如果从低位除起，那么高位除后余下的数退到低位继续除，就会影响原来低位上的商，自然增加了高位有余退位后再除的麻烦。

图2

2.小数四则运算中，相同数位为什么有时要对齐，有时不要对齐？

小数的出现，是基于十进制表示数量的需要，它的计数原则与整数的计数原则相同，所以小数四则计算在很大程度上仿照整数四则计算进行。就像整数的四则计算强调相同数位对齐，小数加减法也一样，需要把相同数位对齐，显著的标志是小数点对齐。但这个看上去顺理成章的规则，在小数乘法里就遭遇了“负迁移”。为什么小数乘法不需要相同数位对齐，而只要把末位对齐就可以了？下面两个学生的错例就是其中的典型。（如图3）

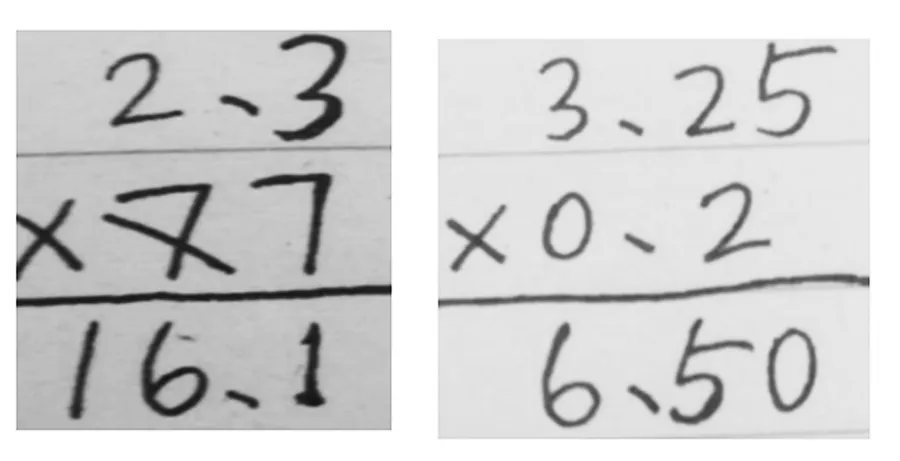
图3

2.3×7中的7为什么要和3对齐？应用积的变化规律，如果先把2.3看成23，那么学生就能理解7要和3对齐了，只不过算出的结果是161个0.1。小数乘小数也一样，3.25×0.2，就是先把它看成325×2，所以竖式中只要末位对齐，其实也就是整数计算中的相同数位对齐，得出结果650，但这是650个0.001，所以正确结果是0.65。

在教学中，也可以借助横式来说明竖式的算理：先让学生充分理解 0.1×0.1=0.01的意义，进而理解0.3×0.2=2×3×0.1×0.1=0.06的意义，再讨论3.25×0.2=325×2×0.01×0.1，大部分学生应该能够逐步理解。

3.分数四则计算中，为什么有的要通分，有的却不要？

在分数的四则计算中，两个分数相加减，先把计数单位转化为相同的，计算时先通分，这样分母不变，分子相加减即可。而表面上看来，对于分数的乘除法来说，却不需要通分：两个分数相乘，分子相乘的积作分子，分母相乘的积作分母；一个数除以分数，等于这个数乘以分数的倒数。其实，在不同的算法表征的背后，也有着相同的算理。所有分数的四则计算都可以看成是分数单位转化为相同的以后的整数运算。（张天孝，2012）

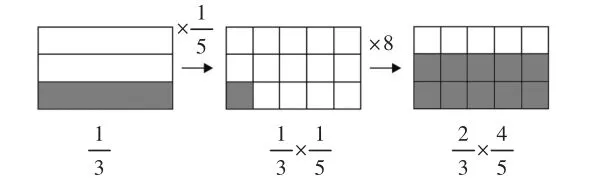
图4

分数除法的算理，可以理解的途径是比较多的，大致有四种。（如图5）第一种是通过把有关分数的运算转化为整数的运算，来解释计算程序的合理性；第二种的依据是商不变规律，把除数部分转化为1；第三种的依据是分式基本性质。基于算理的一致性，本文特别推荐第四种：先把分数单位转化为相同的，即分母相同后，只需把分子相除即可，这又被转化成为分子的运算了，与前面的方法一脉相承。把所有的分数运算都用一个基本的算理沟通起来，便于学生在较低的认知负荷下深入理解。

图5

二 运算能力培养中 “算理”的教学建议

1.创设一个安全的环境让学生自由表达。

语言是思维的外衣。在课堂上，不但要让学生明算理，更要重视让学生说算理。说算理是数学理解和语言表达的综合体现，加强算理的表达也是在培养学生缜密的思维。在日常教学中，我们要着力营造安全的环境，让学生有想说的意愿，有敢说的勇气，还要有会说的能力。很多时候，学生会算，心里也知晓，但就是说不出来。千万不要在一个学生说不清楚的时候，就把他“按”下去，我们要慢慢地启发每一个表达有困难的学生，当众指导一个人，其实受益的是一批人。教学中，还要创造更多的锻炼机会，在小组内提供更多表达的机会，让每一个人都能表达自己的想法。必要的时候，甚至可以提供表达的框架，哪怕是一些关键的字词或短语，如“先……再……最后……”。这能为学生表述算理提供帮助。

2.发生错误时恰是驱动学生说理的最好时机。

正确的解答，有时候可能只是模仿；而错误的解答，却有可能是学生原生态的思考，是宝贵的学习资源。当学生出现错误时，不应急于告诉学生怎么算，矫正比告诉更有意义。抓住学生犯错的时机，及时让学生去辨析、去说理，充分展现学生的思维过程，帮助学生清理阻碍，形成正确的算理。

比如，在两位数乘两位数的竖式计算中，图6中的算法是学生初学时很容易出现的错误，学生不明白为什么第二个“36”要移位。如果简单地告诉学生这个“36”应该写在哪里，那么学生只能模仿，机械计算。

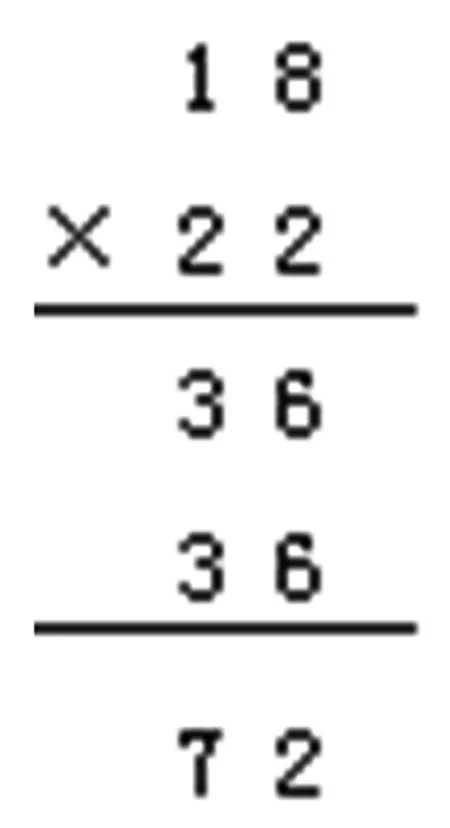
图6

但要帮助学生理解算理，就要从“位值”的角度去引导：十位上的“2”表示2个十，十位上的“2”乘18，结果就是36个十，表示360。教学时，也有学生把乘积个位上的0写出来的，既然用十位上的数去乘结果一定是几个十，个位上一定是0，为了竖式的简洁可以省略不写。这一算理，也可以用乘法分配律去解释，18×22=18×(20+2)=18×20+ 18×2=396。这样做，既可以沟通横式的每一步与竖式之间的联系，也可以多角度理解计算的算理。

3.改变评价方式，增加考核学生理解算理内容的权重。

评价是导向。总有老师错误地认为“算理有什么好说的，还不如多做几道题”。现在的评价改革已悄然转向，命题不仅关注计算技能，而且关注算理理解了。朱乐平老师在“三位数乘两位数”教学中就设计了一系列指向说理的练习题，在说理题的设计方面做了示范。如：根据图7中的乘法算式，可以直接解决下面的问题吗？836×7=（ ）；50160÷60=（ ）；836×7+836×（ ）=（ ）。 还能知道哪些结果？

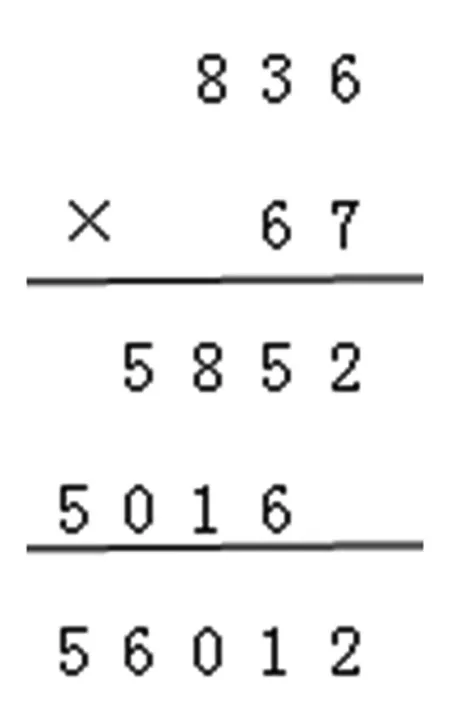
图7

总而言之，理想的数学课堂不仅要让学生“知其然”，还要让学生“知其所以然”，使学生把对法则的演练转变成对算理的思考，把运算从操作层面转向思维层面，从而真正发展学生的运算能力。

（作者单位：浙江金华市金师附小荣光国际学校，杭州市时代小学）