某四塔斜拉桥不同约束体系的动力特性研究

李志山，陈伟明

（广州大学工程抗震研究中心，广州510405）

某四塔斜拉桥不同约束体系的动力特性研究

李志山，陈伟明

（广州大学工程抗震研究中心，广州510405）

依托于琼州海峡大桥的四塔斜拉桥设计方案，研究了在不同塔梁连接方式下结构的自振特性和地震作用下的弹性反应。根据地震分析结果，发现不同频谱特性的地震波对各约束体系影响不同，从而可能会得出不一致的结论。就一般意义而言，全漂浮体系动力性能优于半漂浮体系，而与约束体系相比，其主梁和边塔顶纵向位移都明显更大；全约束体系的抗震性能优于局部约束体系，且对主梁纵向位移约束最强，但与漂浮体系相比其桥塔内力和主梁竖向挠曲都更大。

四塔斜拉桥；约束体系；动力特性；地震响应

Key works：Four-tower cable-stayed bridge；Constraint system；Dynamic property；Seismic response

0 引言

多塔或多跨斜拉桥具有跨越能力强、造价低（与大跨度悬索桥相比）、外形美观等优点，近年来在实际工程中得到了广泛应用[1]，并成为众多大型通道计划中极具考虑价值的结构跨越方案之一。与传统的独塔和双塔斜拉桥相比，在静力性能方面，多塔斜拉桥的中塔两侧没有辅助墩和端锚索限制中塔位移和主梁挠度，因而结构刚度问题突出[2]，另外多塔斜拉桥主梁通常较长，温度变形效应显著；在动力性能方面，多塔斜拉桥整体刚度较小，长周期振动明显，且振型较独塔和双塔斜拉桥更为复杂。在不改变主梁和桥塔截面设计以及全桥立面布置的前提下，通过改变主梁和桥塔的连接方式和在跨中设置伸缩缝或“刚性铰”可以改善全桥刚度和主梁变形性能，从而改善结构的静力、动力性能[3-5]。

多塔斜拉桥塔梁连接方式与其动力性能的关系存在一些普遍性的规律[6]，然而对于不同的桥跨、拉索和索塔的布置，力学行为差异明显，因而动力行为不可一概而论，对于具体的结构方案往往需要具体地分析才能确定合理的塔梁连接方式。本文依托于琼州海峡大桥四塔斜拉桥设计方案，对该结构在不同塔梁连接方式下地震动激励的动力性能进行了研究，并针对不同频谱特性地震波对各约束体系影响不同从而可能得出相矛盾结论的问题进行了简单探讨。

1 动力分析模型

琼州海峡大桥四塔斜拉桥设计方案，立面布置见图1，桥梁全长3 984 m，四塔四索面，其中三主航道斜拉桥部分跨度为1 020m，边墩距辅助墩间跨度为150 m，辅助墩与相邻索塔间跨度为312米，1#、4#边塔由双肢塔柱组成，塔高202 m，2#、3#中塔由四肢塔柱组成，塔高256m，中跨跨中设置刚性铰。主梁采用分离式箱型截面，即将两个扁平钢箱梁平行并列布置，中间采用钢横梁连接，主梁梁高4 m，单幅钢箱梁宽20 m，两幅总桥宽54m，采用正交异性钢桥面板，顶板、下斜腹板及底板均采用U形加劲肋。过渡墩、辅助墩用纵向相对自由、横向约束主梁位移的铰支座模拟，各桥塔与主梁间设置横向抗风支座约束主梁横向位移。各塔、梁、索的材料均采用线弹性的本构模型。假设结构阻尼为瑞利阻尼，第一阶模态的阻尼比为2%。

根据主梁与桥塔在纵向和竖向连接方式的不同，建立5种动力分析体系：①全漂浮体系，即各桥塔与主梁在竖向和纵向均无约束；②半漂浮体系，即各桥塔与主梁仅在竖向有位移约束；③各桥塔与主梁在竖向有位移约束，且在1#、4#桥塔处设主梁纵向位移约束；④各桥塔与主梁在竖向有位移约束，且在2#、3#桥塔处设主梁纵向位移约束；⑤全约束体系，即各桥塔与主梁在竖向、纵向均有位移约束。

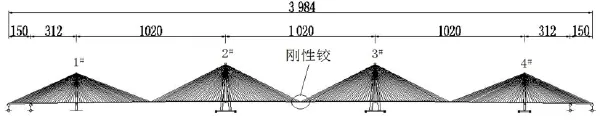
图1 琼州海峡大桥方案动力分析模型Fig.1 Dynamic analysismodel of Qiongzhou Strait Bridge program

2 自振特性分析

由于本文仅研究结构在弹性阶段的动力性能，而弹性阶段的动力反应是各模态动力反应的叠加，因而自振特性分析显得更为重要。按照上节所述的动力分析体系，对5种塔梁连接体系的结构进行了模态分析，结构的前10阶自振周期与振型特征列于表1。根据自振特性的分析结果，可得出以下结论：

（1）整体来看，随着纵向约束的增加，结构纵向刚度变大，各阶纵向自振周期减小。

（2）桥塔与主梁在竖向和纵向的约束情况对结构的横桥向振动影响较小，可近似认为在5种约束情况下主梁和桥塔的横桥向振动模态相同。故对这5种不同约束的结构体系，比选重点在纵桥向振动模态上。

（3）全漂浮与半漂浮体系由于在纵桥向对主梁无直接约束，其第一、二阶模态都呈现出主梁纵漂的长周期振动形式。半漂浮体系在桥塔横梁与主梁相交处设有竖向约束，虽然该约束无法直接限制主梁的纵向位移，但其对与主梁纵漂伴随的主梁竖向弯曲和挠曲有约束作用，该约束作用反过来对主梁纵向位移有一定的限制。上述机理反映到自振特性上就是半漂浮体系纵漂模态的自振周期比全漂浮体系的略短，半漂浮体系各阶主梁竖弯模态的自振周期也比全漂浮体系的略短。而随着纵向约束的引入，纵漂模态消失，且第一阶振型转变为主梁侧弯。

（4）1#4#桥塔设主梁纵向位移约束的结构体系（体系3）与2#3#桥塔设主梁纵向位移约束的结构体系（体系4）的自振周期与振型形状都较接近。两体系的差异在于体系3对边塔区域振动的约束较强，而体系4正好相反。不过从全桥整体刚度特性来看，体系4的刚度要略大于体系3，这是由于体系3在靠近结构两端且刚度较小的两边塔处设置约束，而位于中跨跨中的刚性铰可以释放主梁纵向位移从而削弱了体系3两约束的联系和整体性，因而对全桥整体纵向振动的约束力不及在刚度较大且位于中部的两中塔处设置约束，模型的自振特性也反映了这一观点，体系4的前两阶纵向振动模态的自振周期要小于体系3。

（5）全部桥塔处均设置主梁纵向位移约束的体系5显然对主梁的纵向振动约束最强，表现在自振周期上为其各阶纵向振动模态的周期都小于其它体系相应模态的自振周期。

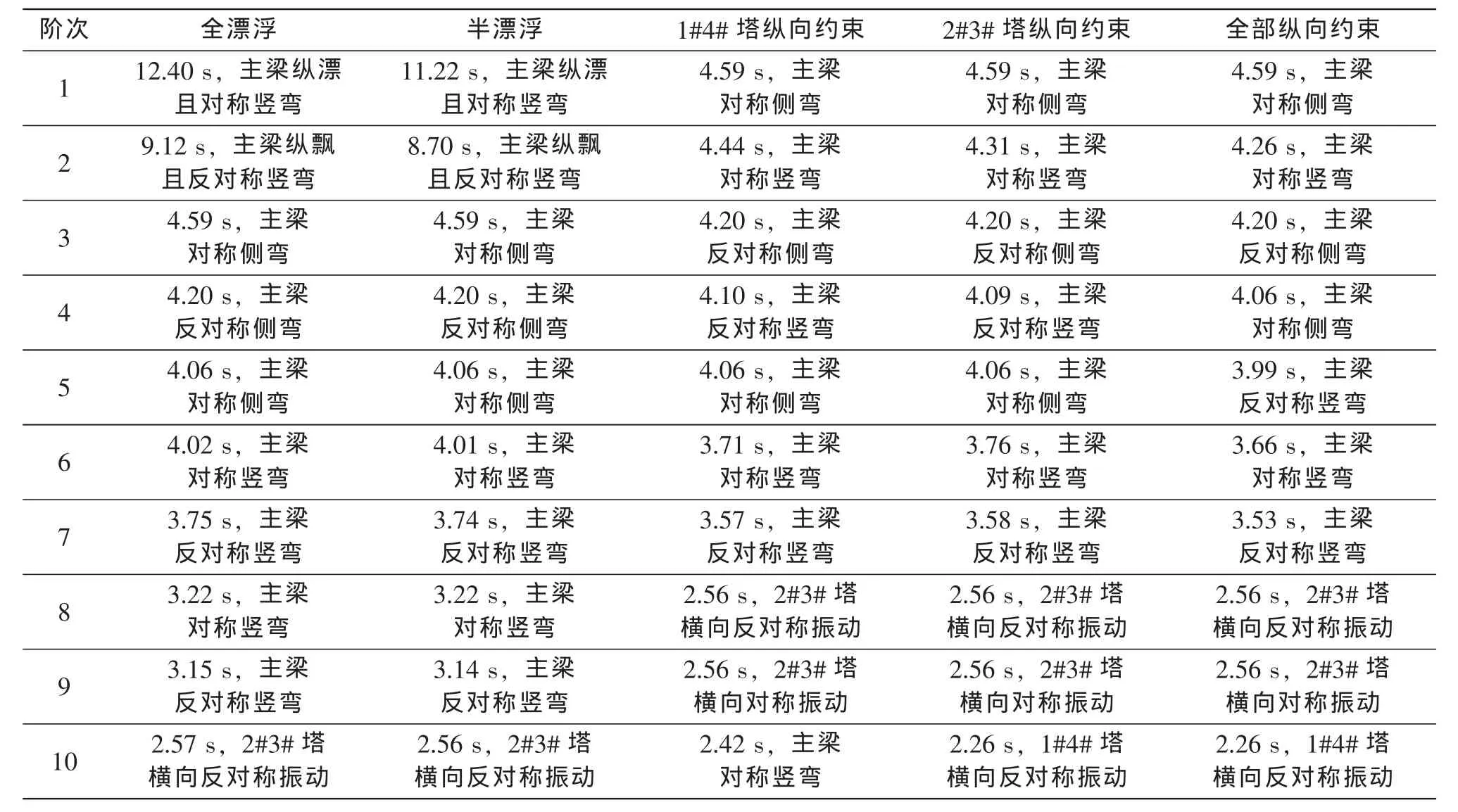
表1 模型自振特性Table 1 Vibration characteristic of themodel

3 一致激励下的动力反应分析

根据上一节的结论，方案比选的重点在纵桥向振动上，因而仅对各结构方案进行纵桥向地震动加载。由于场地条件等情况不明，本文任意选取两条峰值加速度0.35 g、持时20 s的地震波[7，5]分别对5种约束方案进行纵桥向加载。动力时程分析结果表明结构的塔梁连接方式对主梁、各墩顶、塔顶的位移分布与极值，各桥塔塔底轴向力、剪力、弯矩的分配与极值都有显著影响（对于多肢桥塔，以下各内力图所示均为单肢塔柱内力的最大值），在主梁各跨的1/2、1/4、1/8处设置观测点并记录各自的弯矩值。

从各墩塔顶部位移、各桥塔底部受力的角度来看，全漂浮体系和半漂浮体系的动力反应量极值较为接近，无显著差异。然而由图3可以看出，无论在哪个地震波作用下，半漂浮体系都使主梁在2#、3#塔处区域的弯矩极值明显增大。因而如果仅考虑动力性能，全漂浮体系要优于半漂浮体系。

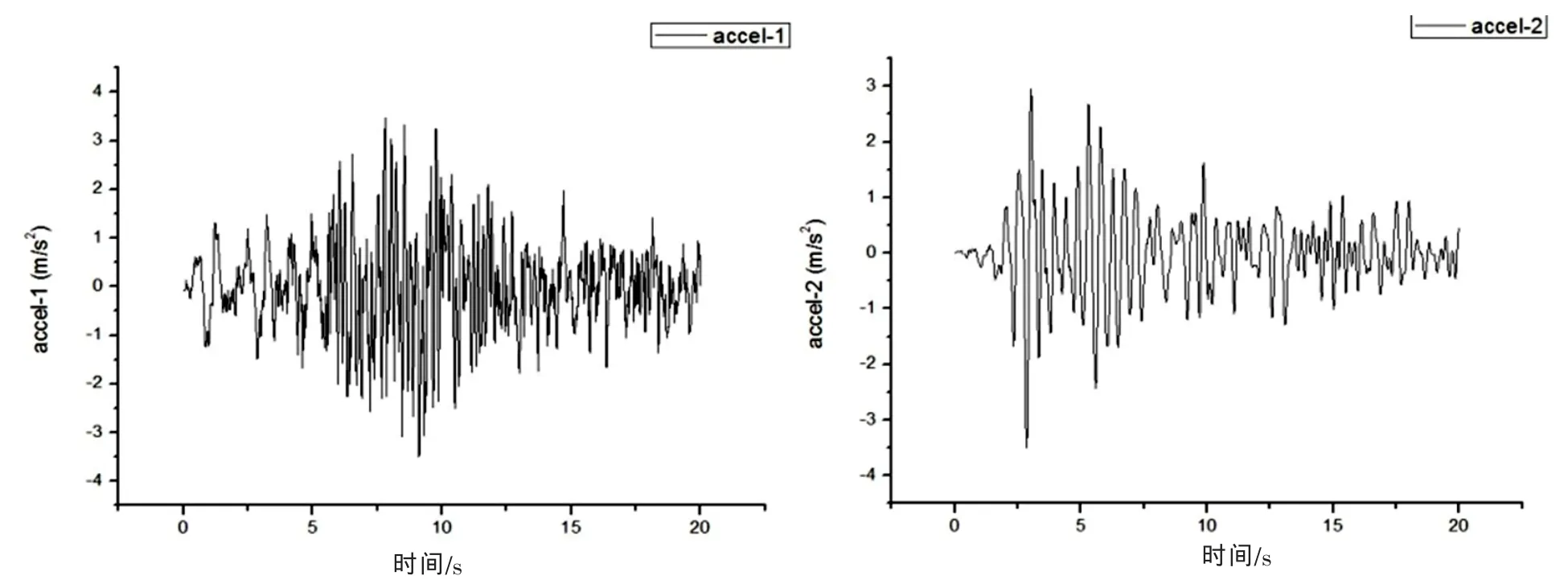
图2 地震波加速度时程Fig.2 Time history of seismic ware acceleration

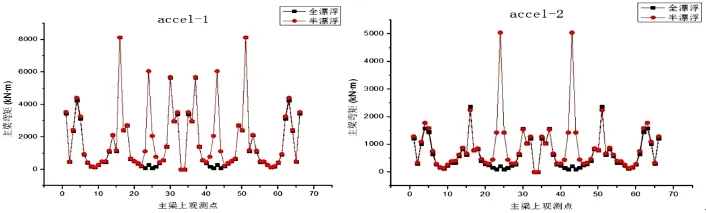
图3 体系1和体系2的主梁弯矩极值Fig.3 The bendingmomentextremum of themain beam in system 1 and system 2

根据两条地震波分别作用下结构的动轴力反应分析结果（见图4），发现随着纵向约束的引入1#、4#边塔的塔底截面轴力极值有所增加。对于由双肢塔柱构成的1#、4#桥塔，其轴力产生的过程是由主梁的振动带动索的变形，而索力的竖向分量产生了桥塔底部的动轴力。不同的纵向约束对主梁在边塔附近纵漂形式位移有不同程度的限制，而对主梁在该处的竖弯振动有不同程度的加强（对于第一条地震波尤为明显），二者联合作用在本桥表现为边塔塔底轴力极值有所增加。而2#、3#中塔的轴力规律较为复杂，2#、3#桥塔由四肢塔柱构成，除去索力竖向分量对桥塔底轴力的贡献外，桥塔的纵向变形也会产生轴力，且这部分轴力因桥塔整体抗弯而产生，其变化规律与桥塔底截面弯矩的变化规律相同。然而对比图4和图7可以发现各种约束方案下2#、3#桥塔底轴力极值曲线与弯矩极值曲线并无明显的相似性，由此可以判断索力竖向分量对轴力极值的影响是很大的。综合来看，从桥塔底部抗轴力的角度，全部桥塔均设置主梁纵向约束的体系5最为合理，其它体系的中塔塔底轴力极值都大于体系5且各桥塔轴力差异也更大。值得一提的是，除了约束体系的差异外，本桥的中塔刚度显著大于边塔刚度也是导致各桥塔内力分配不均的原因之一，然而由于中塔截面强度也大于边塔，故一定范围内的较大内力差异也是可以接受的。

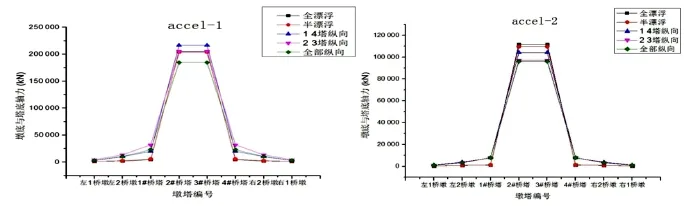
图4 不同约束下各墩塔底动轴力极值Fig.4 The dynamic axial force extremum on the bottom of each pier under different constraints

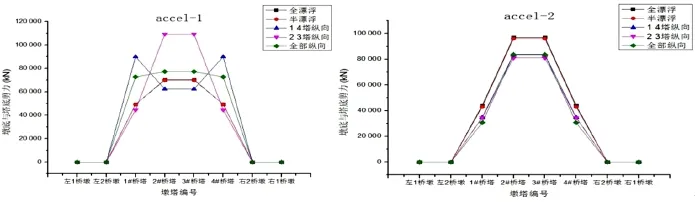
图5 不同约束下各墩塔底剪力极值Fig.5 The shear force extremum on the bottom of each pier under different constraints

由图5中第一条地震波作用下的剪力极值曲线可知释放纵向约束可减小释放约束处的桥塔底部剪力极值，而增加未释放处的剪力，如果纵向约束全部释放成为漂浮体系，则各桥塔底部剪力均减小。对于第一条地震波，只约束1#、4#桥塔处主梁纵向位移的体系3对结构抗剪最不利，因为它将导致较弱的边塔塔柱截面承受比中塔更大的剪力。漂浮体系整体受剪力最小，全约束体系各桥塔所受剪力更大但分配较为均匀。然而结构对第二条地震波的反应却与上述结论相矛盾，在第二条地震波作用下漂浮体系的剪力反应最大，其它约束体系的剪力反应都较小，通过考察两条地震波的频谱（阻尼比为2%的拟加速度反应谱，见图6）可以定性地估计产生上述现象的原因。在长周期区域，第一条地震波的拟加速度反应谱谱值明显更大，这表明整体来看结构对第一条地震波的内力和位移反应较第二条地震波大（各内力图也印证了这一点）。更重要的是注意到第二条地震波在9 s附近（对应漂浮体系的第一阶纵向反对称自振周期）的谱值与4 s附近（对应各纵向约束体系的第一阶纵向反对称自振周期）的谱值大小相当，因而可以推测漂浮体系的第一阶纵向反对称振动模态的剪力反应与约束体系相当，而漂浮体系含有更丰富的频谱构成，故多模态叠加后剪力反应更大也完全可能。对于第一条地震波，9 s左右超长周期对应的谱值远小于4 s左右的谱值，因而约束体系的剪力反应更大。

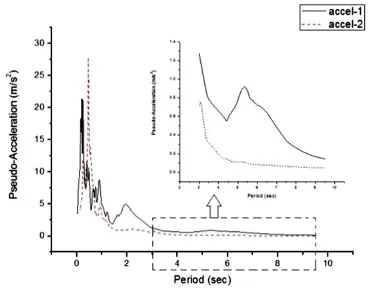
图6 地震波拟加速度反应谱Fig.6 Pseudo-acceleration response spectrum of seismic wave

弯矩的规律与剪力类似，对于第一条地震波，漂浮体系的截面弯矩极值总体最小，且在各桥塔的分布非常均匀，因而对抗弯最为有利。对于剪力显著不均匀分布的约束2#、3#中塔处主梁位移的体系4，其弯矩极值在各桥塔的差异也变小了。上述现象并非偶然，其主要原因是2#、3#中塔各塔柱截面的动轴力对桥塔整体抗弯有一部分贡献，因而中塔各塔柱截面分配到的弯矩有所“降低”。在第二条地震波作用下，类似前面对剪力的分析，由于该地震波的频谱特性，漂浮体系的各塔底弯矩极值大于约束体系。另外由于中塔塔柱动轴力对抗弯的贡献，各体系中塔与边塔弯矩的差异与剪力相比也有所减小。在该地震波作用下，体系4和体系5对抗弯都较为有利（图7）。

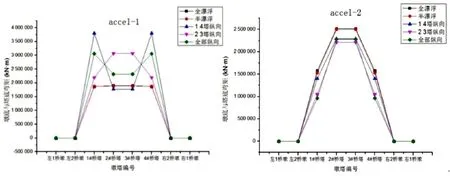
图7 不同约束下各墩塔底弯矩极值Fig.7 The bendingmomentextremum on the bottom of each pier under different constraint

纵向约束的增加对主梁和各塔顶纵向位移的限制作用明显，两条地震波的分析结果都反映了这一点。全部桥塔处均设约束的体系5显然对纵向位移限制最大，而不约束的漂浮体系限制最小。只约束1#、4#桥塔处主梁纵向位移的体系3对边跨区域主梁位移限制较大，而中塔塔顶位移有所加强；只约束2#、3#桥塔处主梁纵向位移的体系4正好相反，而由于全部约束的体系5中塔塔顶位移比边塔大，故放松边塔约束转化为体系4时位移分布变得更为均匀。从限制结构两端墩顶主梁位移的角度，体系3与体系5都较好（图8）。

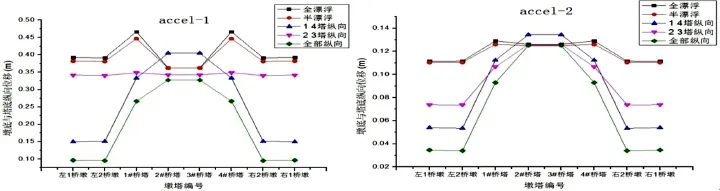
图8 不同约束下各墩塔顶纵向位移极值Fig.8 The longitudinal displacementextremum on the top of each pier under different constraints

两条地震波的分析结果都表明施加了主梁纵向约束后，主梁竖向位移明显变大，尤其是在第一条地震波作用下，纵向约束体系的主梁最大竖向位移超过1m。增加了纵向约束后，结构纵向主要振型由主梁纵漂转变为主梁竖弯，且在边塔附近最为明显，故主梁整体竖向位移随之增大，而边塔附近增量最大。与纵向位移不同，从限制主梁挠曲角度，漂浮体系最为有利（图9）。

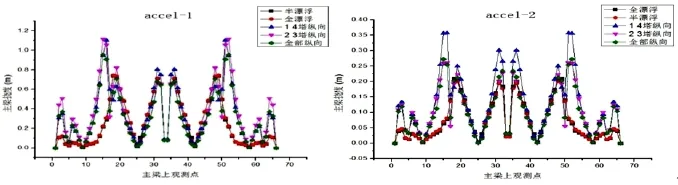
图9 不同约束下主梁竖向位移极值Fig.9 The vertical displacementextremum on the top of themain beam under different constraints

4 结论

根据前文对某四塔斜拉桥动力性能的讨论，归纳出以下结论：

（1）结构的动力响应是由其自身刚度、阻尼等属性和动力激励的幅值、频谱所共同决定的，对本文所讨论的四塔斜拉桥在不同约束体系下的动力响应问题，采用不同频谱特性的地震波可能得出不一致的结论。为消除这种不一致性，可选择多条地震波（调幅后）对结构加载并对反应结果做平均化处理，但是这种调幅和平均的做法缺乏严格的理论基础。更恰当的做法是选择适合结构场地条件的地震波，不过即便是对同一地点的两次地震动记录，频谱特性也可能存在较大差异。因此在实际桥梁抗震设计中选择恰当的地震动输入是需要特别关注的问题。

（2）漂浮体系与半漂浮体系的各桥塔位移、内力反应极值相近，半漂浮体系可能对主梁的纵向位移有不明显的约束，但其使主梁局部受弯矩增大。因而如果仅考虑动力性能，漂浮体系要优于半漂浮体系。

（3）漂浮体系与其它约束体系相比，各桥塔受内力可能最小，但主梁纵向位移最大，且各桥塔尤其是边塔的塔顶位移最大。因而如果要采用漂浮体系，需要特别关注主梁和边塔的纵向位移。

（4）仅约束1#、4#边塔处主梁纵向位移的局部约束体系对边墩顶主梁位移约束较大，但其可能会使边塔承受比中塔更大的内力，而考虑到边塔截面本身就弱于中塔，这种受力模式是不合理的；而仅约束2#、3#中塔处主梁纵向位移的局部约束体系对边墩顶主梁位移约束较小，且中塔静力阶段就承受更大内力，而通过局部约束将有可能把动力也集中于中塔；综上，两种局部约束体系都不理想。

（5）整体来看，全部约束体系无论是在桥塔受力还是主梁纵向位移方面都优于局部约束体系，然而与漂浮体系相比，全部约束体系各桥塔受内力可能更大，更为明显的是其主梁在边塔附近的竖向挠曲显著增大。因而如果采用全部约束体系，需要特别关注主梁在边塔附近的竖向位移。

[1]金立新，郭慧乾.多塔斜拉桥发展综述[J].公路，2010（7）：24-29.

[2]喻梅，李乔.结构布置对多塔斜拉桥力学行为的影响[J].桥梁建设，2004（2）：1-4.

[3]宗霏，周凌远.多塔斜拉桥刚性铰动力分析[D].成都：西南交通大学，2012.

[4]叶爱君，胡世德，范立础.斜拉桥抗震结构体系研究[J].桥梁建设，2002（4）：1-4.

[5]喻梅，李乔.多塔斜拉桥结构特性分析[D].成都：西南交通大学，2003.

[6]彭伟，彭天波，李建中.多塔斜拉桥纵向约束体系研究[J].同济大学学报（自然科学版），2009，37（8）：1 003-1 009.

Research on the Dynam ic Properties of One Four-tower Cable-Stayed Bridge Under Various Constraint System s

LIZhishan，CHENWeiming

（Earthquake Engineering Research&TestCenter，Guangzhou University，Guangzhou 510405，China）

Based upon the design plan of a four-tower cable-stayed bridge for Qiongzhou Strait Bridge,the paper investigates its modal properties as well as its elastic seismic responses under various pylon-girder constraint systems.In terms of the seismic analysis，different seismic waveswith various frequency contentsmay influence bridgemodels differently,and then inconsistent conclusions can be drawn for the cable-stayed bridge under those constraint systems.In general,the dynamic performance of bridge with total floating system is better than bridge with semi-floating system，but compared with pylon-girder longitudinal constraint systems,it has larger girder and pylon longitudinal displacement；the system with all pylons constrained by girder has superior dynamic performance than partial constraint systems，also it has the highest constraint on girder displacement. But compared with floating system，the forces in pylons and the vertical displacementof girder are larger.

P315.9

A

1001-8662（2016）04-0084-07

10.13512/j.hndz.2016.04.013

李志山，陈伟明.某四塔斜拉桥不同约束体系的动力特性研究[J].华南地震，2016，36（4）：84-90.[LIZhishan，CHENWeiming.Research on the Dynamic Properties of One Four-tower Cable-Stayed Bridge Under Various Constraint Systems[J].South china journal of seismology，2016，36（4）：84-90.]

2016-08-26

广州市科技计划项目（2013Y2-00054）

李志山（1966-），男，教授，博士生导师，主要从事结构抗减震数值分析、高性能计算研究.

E-mail：lizhishan@gzhu.edu.cn.