取整函数

张建平

我们看高三模拟考的这道选择题：个案1：对于任意实数x，[x]表示不超过x的最大整数，如[1.1]=1，[-2.1]=-3.定义在R上的函数f（x）=[2x]+[4x]，若A={y|y=f（x），0≤x≤1}，则中所有元素的和为（ ）

A.10 B.14 C.15 D.13

这道题，学生望而生畏，大部分学生都是通过猜来完成解答的.“畏”产生在取整函数模糊、不熟悉，遇到这类问题无从下手，找不到破解的方法.本题答错的学生多，教师如何解决，若再碰到取整函数问题又如何应对，教师在讲题时不能就题讲题，否则今后学生碰到此类题型做对的学生不会增多，如何引申拓展教学，我在教学中探究设计如下.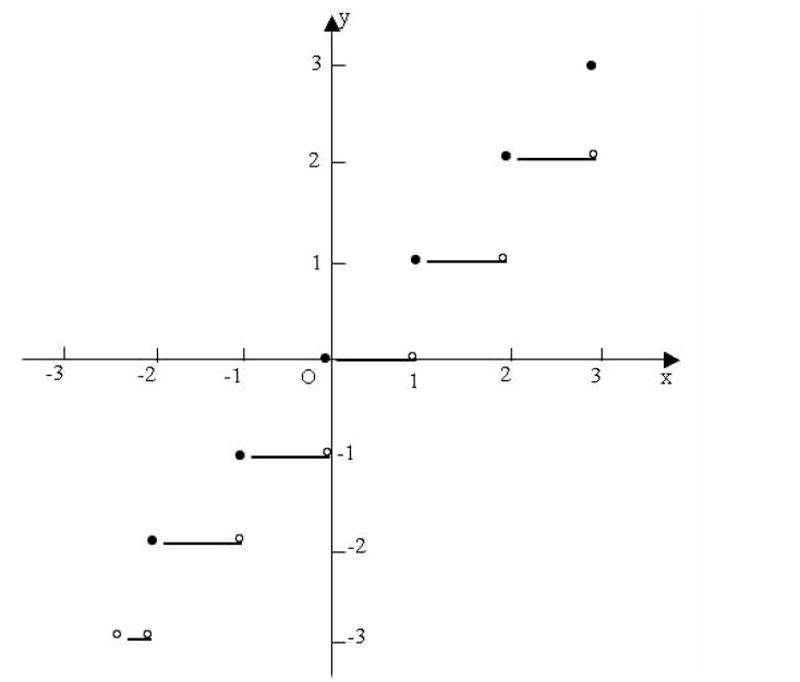

1.题目背景

找到取整函数在课本中的“影子”复习基本概念和解题方法，为解个案2打开学生的思路.

课本必修一第一章第25页有这样一道习题：

个案2：函数f（x）=[x]的函数值表示不超过x的最大整数，例如，[-3.5]=-4，[2.1]=2.当x∈（-2.5，x]时，写出函数f（x）的解析式，并作出函数的图像.

从取整函数的意义可知f（x）=[x]的定义域是R，值域是Z.教师分析时注意题中给出的定义域x∈（-2.5，3]，联系取整函数的意义，从“例如”告诉我们可以将取整函数f（x）=[x]用分段函数来表示，并且每段的定义域区间的长度都是1，这是解有关取整函数问题的关键点.这样很快得到解析式，图像也可以画出，图像呈阶梯状.

我们就可以从中得到启发，学生也许就有思路了.

这时再给时间让学生思考，然后通过提问师生共同解决.

解：个案1给出的函数是与取整函数有关联的函数，由集合的意义和已知本题即是求在定义域所有函数值的和.

解题的关键点是将0≤4x≤4分成区间长度为1的5段进行讨论.

综上可知，A中所有元素的和为：0+1+3+4+6=14.

2.拓展引申

继续巩固现有成果，再扩大战果，看下面与取整函数有关的题型.

Ⅰ、取整函数与不等式：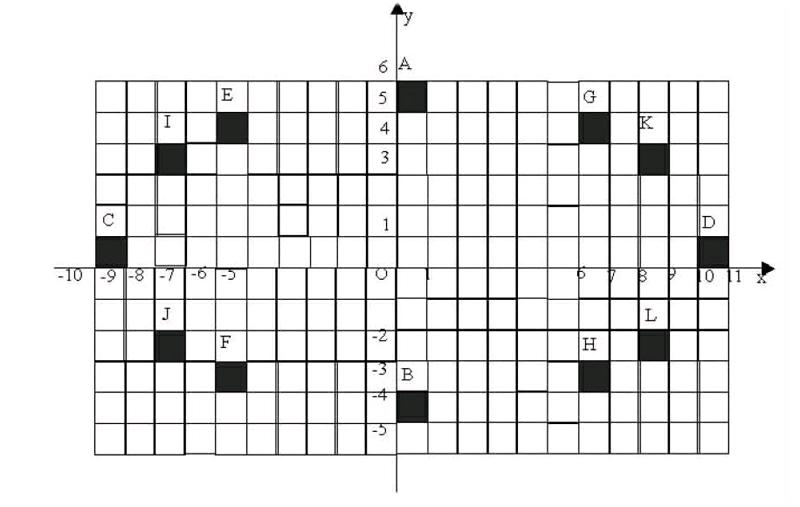

个案3：若[x]表示不超过实数x的最大整数，则不等式[x]≥x-1的解集是（ ）

分析：可利用图像法解，令y=[x]，y=x-1，

问题等价于当函数y=[x]的图像在抛物线y=x-1的上方时，

求横坐标x的取值范围.

如下图，两个函数图像的交点为A（x，1）.

Ⅱ.取整函数与数列：

个案4：若x∈R，记不超过x的最大整数为[x]，

令{x}=x-[x]，则（ ）

A.是等差数列但不是等比数列

B.是等比数列但不是等差数列

C.既是等差数列又是等比数列

D.既不是等差数列又不是等比数列

分析由取整函数的意义，

三数构成等比数列.

Ⅲ.取整函数与方程：

个案5.设[m]表示不超过实数m的最大整数，则在直角坐标平面xOy上满足[x]+4[y]=100的点P（x，y）所形成的图形的面积为（ ）

A.10 B.12 C.10π D.12π

分析：我们在解决这个方程：[x]+4[y]=100，不考虑正负，[x]，[y]的整数解有四组，

（0，5），（10，0），（6，4），（8，3）

（1）当|[y]|=5时，5≤y<6或-5≤y<-4，由[x]=0，∴0≤x<1，围成的区域是两个单位正方形A，B；

（2）当|[x]|=10时，10≤x<11或-10≤x<-9，由[y]=0，∴0≤y<1，围成的区域也是两个单位正方形C，D；

（3）当|[x]|=6时，6≤x<7或-6≤x<-5，再由|[y]|=4，4≤y<5或-4≤y<-3，围成的区域是4个正方形E，F，G，H；

（4）当|[x]|=8时，8≤x<9或-8≤x<-7，再由|[y]|=3，3≤y<4或-3≤y<-2，围成的区域也是4个正方形I，J，K，L.共12个单位正方形，图中阴影部分的正方形所环绕的图形是一个椭圆，故点P（x，y）所形成的图形的总面积为12，答案选B.已知方程就是由焦点在x轴上的椭圆变式而来.本题从给定方程，利用取整函数的意义，确定出满足方程的整点，对整点进行分类讨论，化归转化为函数图形，以形助数通过图形确定出面积.

3.归纳小结

取整函数（高斯函数）的性质：

我们再看下面一道高考题（2013年陕西卷理科选择题最后一题第10题）.

个案6.设[x]表示不大于x的最大整数，则对任意实数x，y，

设[x]表示不大于x的最大整数，则对任意实数x，y，有（ ）

故C错；由排除法知，选D.

从以上6个案，学生对取整函数会有新的认知，解有关取整函数问题的解题思路是抓住取整函数的意义，根据已知条件，抓住所问，或利用特值法或利用化归为分段函数（合理划分区间长度为1的每段是解题的关键点）或图像法或利用其性质解题等，学生通过积累，今后再碰到取整函数问题，至少可为解此类题型提供思路和方向，同时也有利于在考试时增强自信心.

参考文献：

[1]杨炼.直角三棱锥的一个存在条件——从一道模考错题谈起.数学教学研究，2004（05）.