燃气文丘力空气引射器的数值模拟研究
李成明,徐江荣
(杭州电子科技大学能源研究所,浙江 杭州 310018)
燃气文丘力空气引射器的数值模拟研究
李成明,徐江荣
(杭州电子科技大学能源研究所,浙江 杭州 310018)
摘要:在原有自行设计的多引射旋转预混燃烧器基础上,利用FLUENT软件对该燃烧器的引射器的喷嘴入口长度参数进行优化.综合考虑引射器的引射系数、混合燃气在出口处的一次空气系数和混合当量比系数,优化精度达到1 mm.采用二分搜索法搜索引射系数为最佳的工况——最佳的喷嘴入口长度;再以最佳工况为中心,选取5个工况分析出口的一次空气系数和混合当量比系数,综合考虑并最终得出最优喷嘴入口长度参数.结果表明,最优喷嘴入口长度为距空气入口5 mm处,并分析了此时各横截面和中心轴线上的速度、压力分布情况.
关键词:引射器;最优喷嘴入口长度;引射系数;一次空气系数
0引言
引射器是大气式燃烧器和全预混燃烧器中最重要的几何结构.国内外许多学者都对燃气灶的引射器进行了相关研究,文献[1]采用实验方式和数值模拟方式对某上进风燃气灶进行了研究,得到了数值模拟结果与实测的气相色谱分析数据基本一致的结果,验证了利用数值模拟方式来分析引射器的引射能力的可行性和可靠性.文献[2]通过实验研究了喷嘴位置对小容量喷射式制冷的影响,结果表明,对于不同的工况条件,喷嘴的最佳位置是不一样的.文献[3]研究了喷嘴位置对大气式燃烧器的引射器的一次空气系数的影响,得出喷嘴入口长度为1 mm时,引射器引射性能最佳,但并未考虑引射器的引射系数和混合气体的混合当量比系数.文献[4]对上海林内2M2F燃烧器的引射器进行了数值模拟和实验研究,分析了引射器的引射系数、一次空气系数和中心轴线上的混合燃气的当量比系数,但并未进行引射器的参数优化.鉴于前人对引射器的研究,本文使用实验和数值模拟相结合的方式,采用二分搜索法对引射器的喷嘴入口长度参数进行优化,从而实现改进和优化原自行设计的燃烧器的目的.
1实验装置及原理
本文实验时会消耗大量的燃气(甲烷),出于成本和安全性考虑,实验时使用空气代替燃气作为工作流体,实验系统由供气系统、质量流量控制系统、喷嘴、文丘力管(引射器)、测量系统组成,如图1所示.

图1 实验系统图
引射器的引射能力主要由引射系数来描述,引射系数α为:

(1)
式中:mg为引射流体入口质量流量,mw为工作流体入口质量流量.
喷嘴安装在导轨上,实验时,根据不同的喷嘴入口长度调整导轨的进给长度,利用SYT-2000微电脑数字压力计和S型毕托管测出引射器出口风速,通过计算得到出口质量流量,出口质量流量减去工作流体入口质量流量即为引射流体的入口质量流量,再根据式(1)计算得到引射系数.
2几何模型及数值计算
引射器的工作流体(燃气)为甲烷,入口速度为25.5L/min(一般实验工况).引射流体为空气,压力为标准大气压,其他参数见图2.图2中,L为喷嘴入口长度参数,为可变参数(研究对象),截面1-1为喷嘴出口截面,单位为mm.
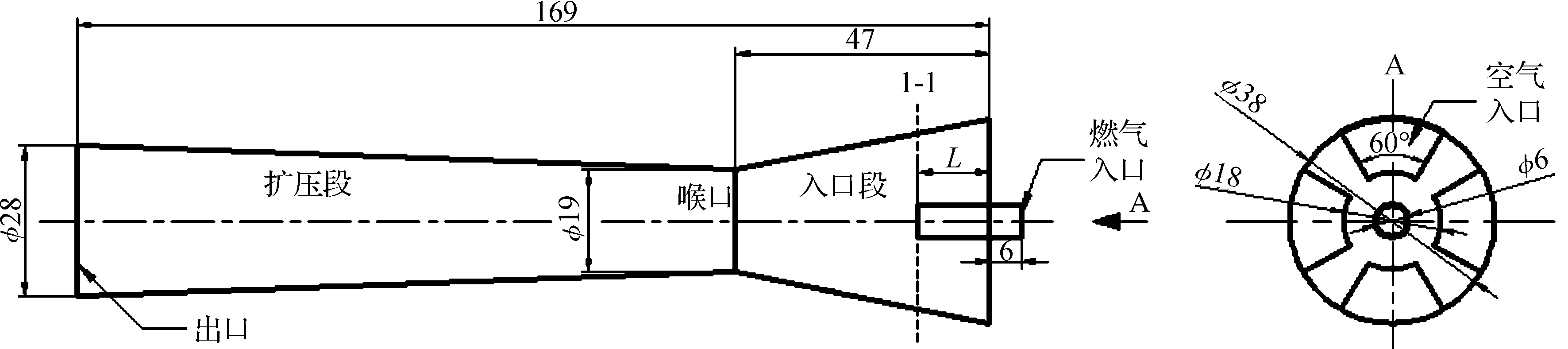
图2 引射器几何结构截面图
划分网格时,由于引射器入口段结构比较复杂,而其他结构比较简单,因此为了提高网格质量、降低网格数量和节约计算时间,采用混合网格方式划分网格,入口段使用喷嘴出口截面切分,首先对喷嘴出口截面的喷嘴口划分线网格,再对喷嘴出口截面划分面网格,对入口段靠近空气入口部分采用非结构网格划分体网格,其他部分均采用结构网格划分体网格,各工况网格数量均在68万个节点以上,网格单元大小的歪斜度(EquiSize Skew)在0°~0.4°之间的网格数均大于95.82%,网格质量很好.
燃气入口定义为速度入口边界,速度大小设为11.789 m/s(由实验工况换算而来),水力直径为6 mm;空气入口定义为压力入口边界,全压设为0 Pa,水力直径为11.89 mm;出口定义为压力出口边界,根据文献[5],出口全压设为1.4 Pa,水力直径为28 mm.
引射器的主要原理是:工作流体经喷嘴高速喷出,形成射流,通过卷吸流动将引射流体卷入,在引射器内部工作流体和引射流体进行动量交换,速度逐渐趋于均匀.甲烷入口截面处的雷诺数为4 346.204>4 000,引射器内的流动为湍流,引射器内涉及到两种流体的输运,故在利用Flunt求解器进行数值计算时,需要用到湍流模型和输运方程模型.
为了简化实际问题,便于分析,本文做出如下基本假设:1)由于燃气压力较低,甲烷可视为不可压缩流体;2)流动温度为常温,密度可视为常数;3)引射器内流体的流动为稳态湍流,引射器壁面上满足速度无滑移边界条件.
标准κ-ε湍流模型应用广,能满足一般的收敛性和精度要求,计算时间较短,适合于完全湍流模型.本文引射器内部为完全湍流,对收敛性和精度要求不高,计算时间要求尽量短,因此湍流模型采用标准κ-ε湍流模型.
FLUENT求解器设为压力基和稳态,组分输运混合物为甲烷—空气(methane-air),甲烷入口边界组分中甲烷设为1,空气入口边界组分中氧气设为0.21,控制方程使用SIMPLE求解公式,离散格式使用二阶差分迎风格式.
为了节约计算时间,首先,对L=2 mm,6 mm,10 mm,14 mm,18 mm,22 mm,26 mm,30 mm,34 mm,38 mm,42 mm,47 mm(喉口)的12个初始工况进行计算,得出此时引射系数最大时的喷嘴入口长度工况,并记为Lmax0;再次,以Lmax0为中心,采用二分搜索法搜索出引射系数为最大的喷嘴入口长度工况,并记为Lmax.最后,以Lmax为中心,选取5个工况进行综合考虑.实际计算所用工况为L=2 mm,3 mm,4 mm,5 mm,6 mm,7 mm,10 mm,14 mm,18 mm,22 mm,26 mm,30 mm,34 mm,38 mm,42 mm,47 mm,共为16个工况.
3结果分析
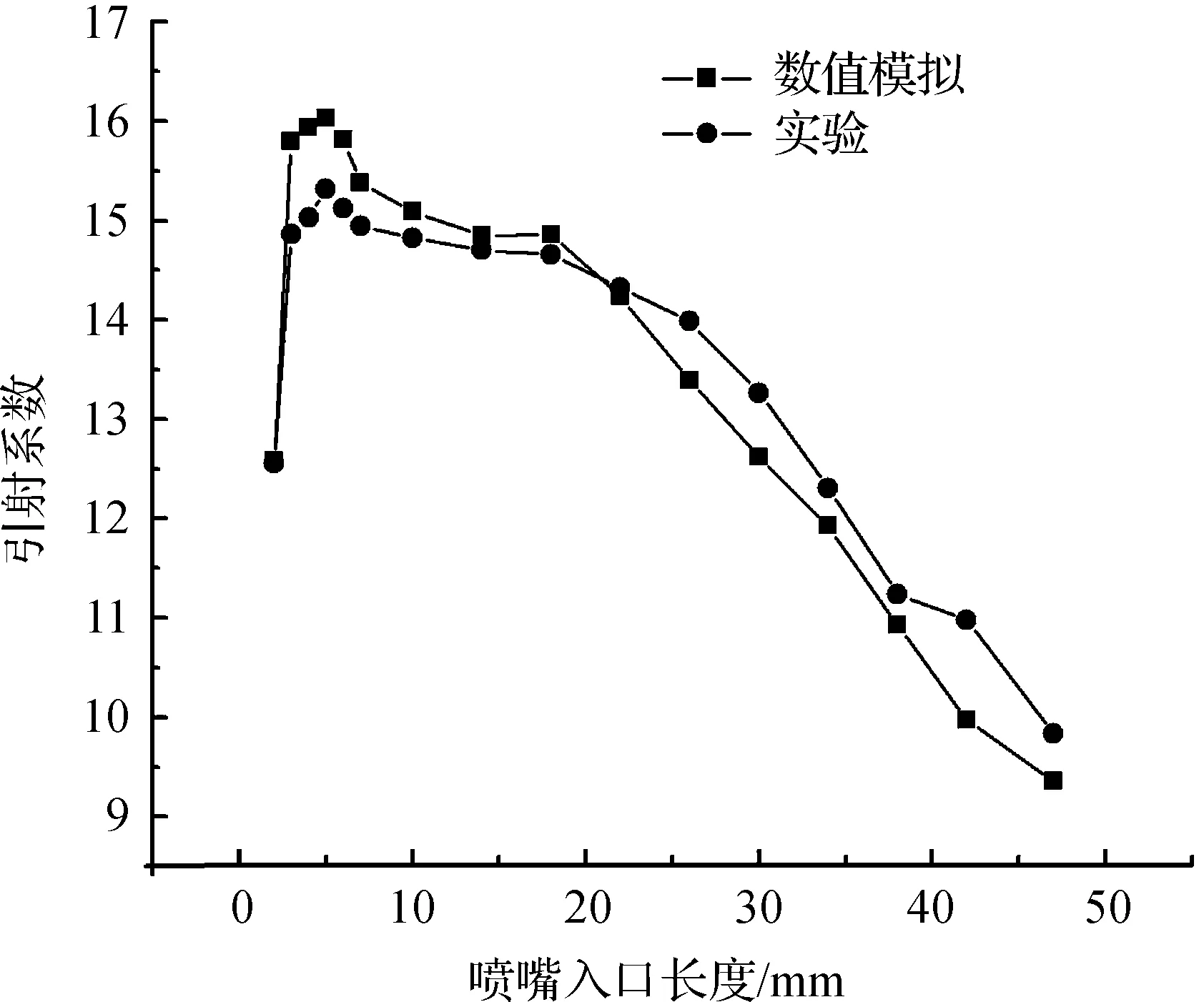
图3 不同工况下引射系数关系图
图3为不同喷嘴入口长度工况下引射系数关系图.由图3可以看出,实验结果与数值模拟结果基本一致,表明数值模拟具有很好的可靠性.当L=5 mm时,引射系数最大,为16.024,α与L近似为抛物线分布,这也是本文使用二分搜索法的前提.原因是:当L为0~5 mm时,虽然甲烷流速随着L的增加而有所降低,但空气入口的有效面积却快速增加,此时空气入口有效面积的增大比甲烷流速降低对引射器的影响作用更大,α增大;但当L>5 mm时,空气入口有效面积增长缓慢,同时甲烷流速降低明显,此时甲烷流速降低对引射器的影响作用更大,α开始减小.
为了减少分析次数,以Lmax为中心(最优工况在Lmax附近),首先选取5个工况进行一次空气系数和混合当量比系数分析,一次空气系数β和混合当量比系数φ为:
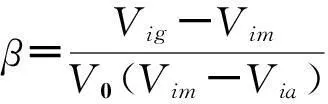
(2)
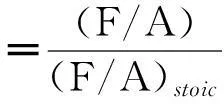
(3)
式中:Vig为燃气中i组分的体积分数,Vim为空气中i组分的体积分数,Via为混合气体中i组分的体积分数,V0为标准状态下1m3的燃气燃烧所需的理论空气量,对于甲烷则为9.555 4,(F/A)stoic为化学恰当反应时燃料—空气摩尔体积比,对于甲烷为0.5,F为燃料甲烷的体积流量,A为空气体积流量.
根据式(2)和式(3),分别计算出5个工况下出口的β和φ,分别如图4和图5所示.由图4和图5可知,当L=5mm时,β最大,为0.411,但是此时的φ最小,为1.352 192 088>1,表明此时甲烷与空气混合完全均匀,且甲烷过剩.参数优化时最理想的情况是在某喷嘴入口长度工况下,引射系数最大,一次空气系数最接近1,混合当量比系数最接近1.本文中在L=5mm时即为最理想的情况,因此,此时即为引射器的最佳喷嘴入口长度,并将此工况视为最优工况.
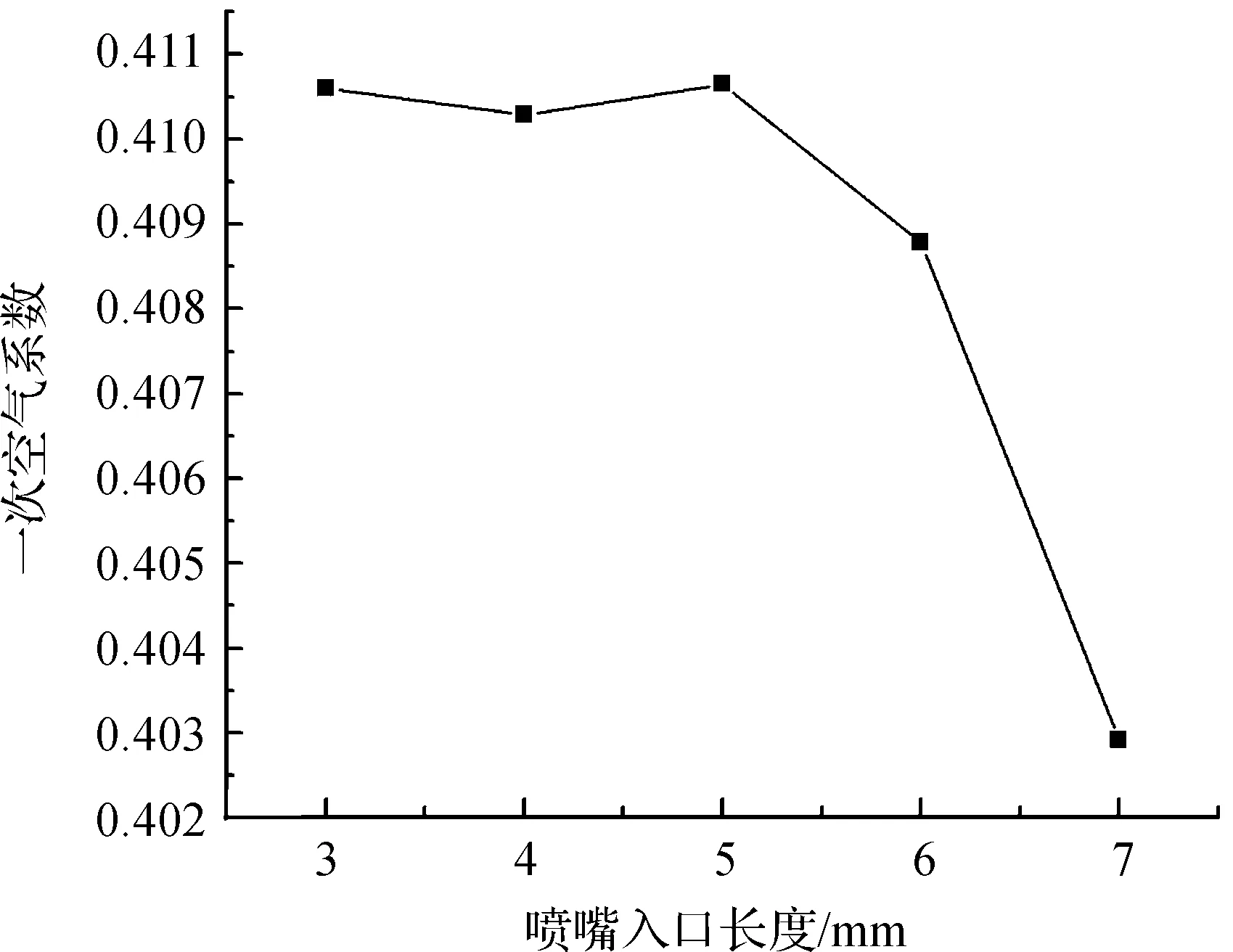
图4 不同工况下出口的一次空气系数关系图
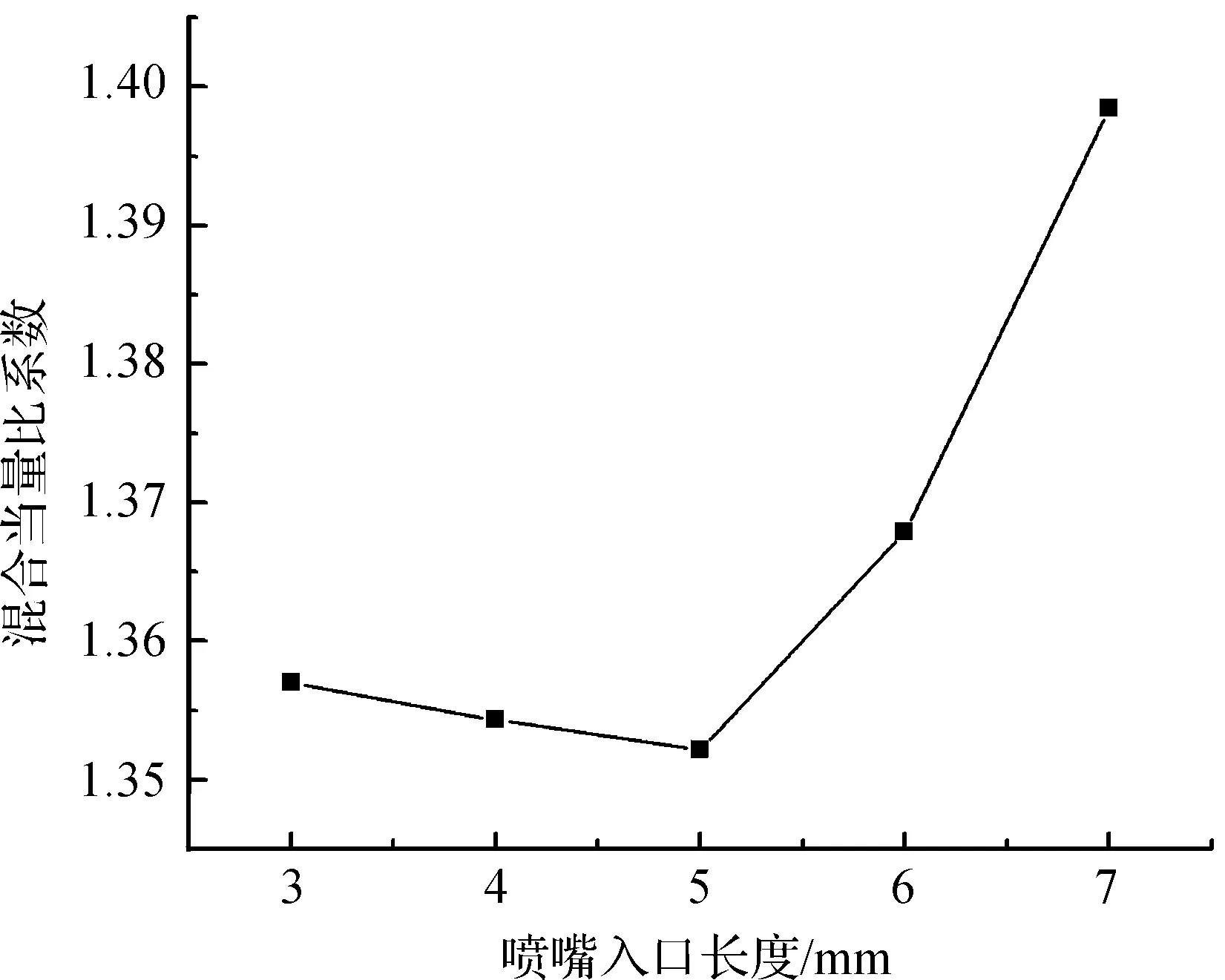
图5 不同工况下出口的混合当量比系数关系图
图6为最优工况下的速度分布,图6中,(a)为不同横截面x(初始位置为空气入口,x=0)的速度分布,(b)为中心轴线上速度分布.由图6可以看出,甲烷引射空气后,混合燃气的速度在喉口截面处(x=-47 mm)附近先上升后下降;空气入口截面(x=0)在-0.019~-0.009 m和0.009~0.019 m(空气入口)之间具有很明显的速度分布,这说明引射器将空气从空气入口引到射器内;同时,混合燃气的速度在扩压段后段逐渐趋于缓和,表明甲烷与空气充分混合了.
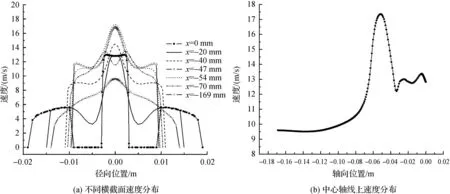
图6 最优工况下的速度分布
图7为最优工况下的压力分布,图7中,(a)为不同横截面的压力分布,(b)为中心轴线上速度分布.由图7中可以看出,甲烷经喷嘴喷出后,在引射器内部形成负压且压力不断降低,并在喉口截面附近压力降到最低,表明引射器内部与空气入口产生了正压差,并通过压差作用将空气压入引射器内,最大压差为-66.320 1 Pa,表明引射器的抽吸力很强,在扩压段,压力不断回升,并最终趋于平均,表明甲烷与空气充分混合了.

图7 最优工况下的压力分布
4结束语
本文经实验和分析得出,燃烧器的引射器喷嘴入口长度的最佳参数为5 mm,优化了原自行设计的燃烧器的引射器结构参数,提高了引射器的工作性能.与其他文献不同,本文在优化时采用引射系数来衡量引射器的引射能力,混合燃气在出口截面的一次空气系数和混合当量比系数来衡量引射器的混合特性,在考虑最优参数时,综合考虑引射器的引射能力和混合特性.由于本文将引射器单独建模,并进行冷态分析,因此结果与实际的工程应用会有一定的偏差.在今后的研究工作中,将对整个燃烧器进行建模,并引入燃烧模型,更加精确地模拟燃烧器的实际工作过程.
参考文献
[1]郭甲生,秦朝葵,孙秀丽.上进风燃气灶引射性能的数值模拟[J].工业加热,2008,37(2):12-15.
[2]RUANGTRAKOON N,APHORNRATANA S,SRIVEERAKUL T. Experimental studies of a steam jet refrigeration cycle:effect of the primary nozzle geometries to system performance[J]. Experimental Thermal and Fluid Science,2011,35(4):676-683.
[3]方媛媛,郭全.喷嘴位置对引射器性能影响的数值模拟[J].煤气与热力,2007,27(7):42-44.
[4]倪娟娟,张海军.大气式燃烧器内引射器的数值模拟与实验研究[J].上海煤气,2012(2):22-25.
[5]冯良,刘鲲,韩国园,等.大气式燃气燃烧器引射器的CFD研究[J].上海煤气,2003(2):13-16.
Parameter Optimization of Domestic Gas Burner Injector
LI Chengming, XU Jiangrong
(InstituteofEnergy,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Abstract:This paper optimizes parameter of the nozzle inlet length of a self-designed ejector that was installed in a multi ejector tangential premixed burner by using FLUENT software. 3 parameters are considered comprehensively: the ejecting ratio, primary air coefficient and mixed equivalence ratio coefficient. Optimization precision is 1 mm. Firstly, searching the best working condition—the best nozzle inlet length that the ejector coefficient is best by using the binary search; once again, analyzing primary air coefficient and mixed equivalence ratio coefficient of the mixed gas in the outlet section of the 5 conditions that is selected centering on the best working condition, and obtaining the optimal parameter of the nozzle inlet length by considering comprehensively the ejecting ratio, primary air coefficient and mixed equivalence ratio coefficient of the mixed gas in the outlet section of the 5 conditions. The results show that the optimal parameter of the nozzle inlet length is 5 mm from the air inlet section, and analyzing the velocity and pressure distribution of the cross section and the central axis of the condition, which is the optimal nozzle inlet length.
Key words:ejector; the optimal nozzle inlet length; the ejecting ratio; primary air coefficient
DOI:10.13954/j.cnki.hdu.2016.02.019
收稿日期:2015-10-08
基金项目:浙江省自然科学基金资助项目(LY15E060007)
作者简介:李成明(1990-),男,贵州施秉人,硕士研究生,动力机械热流理论与数值模拟研究.通信作者:徐江荣教授,E-mail:jrxu@hdu.edu.cn.
中图分类号:TK16
文献标识码:A
文章编号:1001-9146(2016)02-0089-04

