基于跨组生长与生态平衡种群模型的最优收获

郭冬雪，何泽荣，李晨晨

(杭州电子科技大学运筹学与控制论研究所，浙江 杭州 310018)



基于跨组生长与生态平衡种群模型的最优收获

郭冬雪，何泽荣，李晨晨

(杭州电子科技大学运筹学与控制论研究所，浙江 杭州 310018)

摘要：考虑一类跨组生长的离散尺度结构种群模型，个体按照尺度由小到大被分为3个小组，既考虑跨组生长也顾及生长迟缓情形.在生态平衡约束下研究最优收获问题，应用凸集上的函数极值理论导出了两阶段模式的最优收获策略，具体收获比例由模型参数确定.研究结论表明，资源管理领域的“双窗原理”在一定条件下对非正常演化的尺度结构种群仍然成立.

关键词：尺度结构；跨组生长；离散种群模型；最优收获策略

0引言

对许多种群而言，用差分离散模型描述其演化是很方便的[1-2]，近半个世纪以来，离散年龄结构生态模型的研究取得了显著成就，比如，文献[3]针对一类Leslie矩阵模型，讨论生态平衡制约下各年龄组个体的最优收获问题，获得了两阶段策略；而文献[4]则研究McKendrick种群模型的收获问题，结果显示，最优策略是至多收获3个不同的年龄段.尺度结构模型比年龄结构更加接近实际.文献[5]探究了具有跨组生长现象的尺度结构种群的演化行为，文献[6]研究了投放环境下的种群演化，文献[7]研究了一类离散尺度结构模型的最优收获问题.本文进一步考虑个体跨组生长行为，探讨一类离散尺度模型的最优控制问题.

1种群模型

考虑如下具有3个尺度小组的种群模型：

N(t+1)=AN(t),t=0,1,2,…,

(1)

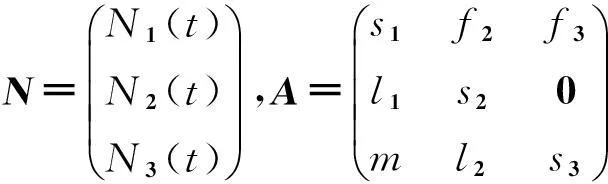
再令yi(0≤yi≤1,i=1,2,3且y1≠1)表示对第i组个体的收获比率，用收获矩阵Y表示如下：

(2)

为了资源的可持续利用，人类对种群收获后依然要保持生态平衡，则种群要满足条件：

(E-Y)AN=N,

(3)

(4)

2最优收获策略

令1-yi=λi,i=1,2,3，则方程(E-Y)AN=N即为：

(5)

由式(5)知：

(6)

将式(6)代入式(5)中的第1个式子，得：

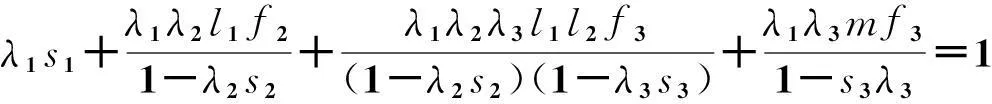
(7)

(8)

记(A-E)v=b，即b1=(s1-1)v1+l1v2+mv3,b2=f2v1+(s2-1)v2+l2v3,b3=f3v1+(s3-1)v3.

由式(6)和式(8)得：

(9)

记

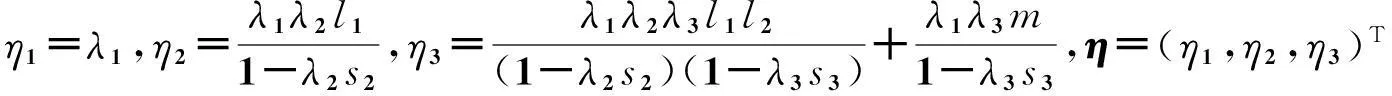
(10)

得出：

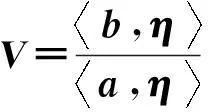
(11)

由于向量a,b是已知的，因此要求V的最大值只需确定η.记

ζ1=s1,ζ2=f2,ζ3=f3,ζ=(ζ1,ζ2,ζ3)T.

(12)

综上所述，最优收获问题的容许变量集合为：

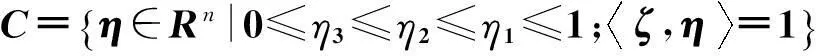
(13)

文献[7]证明了如下结果：首先对n个尺度小组种群定义，Di=ζ1+ζ2+…+ζi=s1+f2+…+fi,Bi=a1+a2+…ai,i=1,2,…,n.

引理如果Dn>1,li-1+si=1,i=2,…,n,且满足以下条件中任一条件：

1)Bi≥0,i=1,2,…r-1;Bi>0,i=r,r+1,…n.

则种群的最优收获策略存在，最优收获策略为：

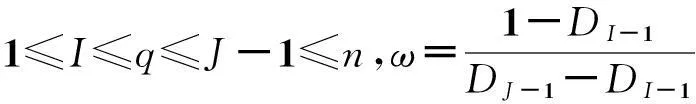
应用以上引理可得如下最优收获策略：

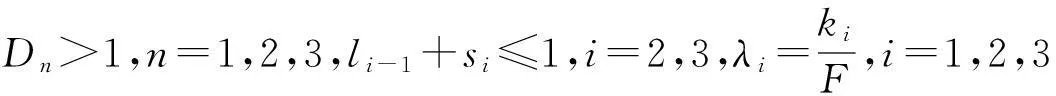
3结束语

本文采用的模型有两个主要特点：一是跨组生长，二是保持平衡.种群个体分为3个小组，研究结果表明，两阶段策略仍为最优，第一组个体不予收获.这既有理论依据，也与实践经验吻合，故幼体应该保留.另一方面，分组数目多于3时，相应的跨组生长模型收获问题无法运用本文的思路，需要进一步探索其它途径.关于模型的实际应用，由于经过对个体的收获以后，单位时间内种群数量应该复原，因此时间单位的选择不能太短，一般以年为单位为宜.

参考文献

[1]BRITTON N F. Essential Mathematical Biology[M].Beijing: Tsinghua University Publishing, 1990：30-34.

[2]陈兰荪,宋新宇,陆征一.数学生态模型与研究方法[M].成都：四川科学技术出版社, 2003：55-88.

[3]RORRES C, FAIR W. Optimal harvesting policy for an age-specific population[J]. Mathematical Biosciences, 1975, 24(1)：31-47.

[4]MURPHY L F, SMITH S J. Optimal harvesting of an age-structured population[J]. Journal of Mathematical Biology, 1990, 29(1)：77-90.

[5]周娟,何泽荣,郑敏.跨组生长与离散尺度下的种群模型的演化行为[J].杭州电子科技大学学报,2013,33(3)：89-92.

[6]邹世平,何泽荣,杨立志.具有投放和选择性捕捞的种群模型研究[J].杭州电子科技大学学报,2014,34(5)：43-47.

[7]何泽荣,吴鹏,周娟.生态平衡制约下离散尺度结构种群的最优收获[J].高校应用数学学报A辑,2015,30(2)：171-179.

Optimal Harvesting of Discrete Size-dependent Population Based on Ecological Balance and Group-crossing Growth

GUO Dongxue, HE Zerong, LI Chenchen

(InstituteofOperationalResearchandCybernetics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Abstract：This paper considers a class of discrete size-structured population model with group-crossing growth, and the individual is divided into three groups from small to large. Both the cross and slow growth are taken account. Also, it investigates an optimal harvesting problem under the constraint of ecological balance. By means of the extreme theory of functions on convex sets, the optimal strategy is obtained and the specific harvest ratio is determined by the model parameters. The conclusion shows that “double windows principle” in the resource management field is still established for the non-normal evolution of size-structured population under certain conditions.

Key words：size-structure; group-crossing growth; discrete population model; optimal harvesting strategy

DOI：10.13954/j.cnki.hdu.2016.02.016

收稿日期：2015-10-12

基金项目：国家自然科学基金资助项目(11271104)

作者简介：郭冬雪(1990-)，女，河南濮阳人，硕士研究生，运筹学与控制论.通信作者：何泽荣教授，E-mail：zrhe@hdu.edu.cn.

中图分类号：O175.1

文献标识码：A

文章编号：1001-9146(2016)02-0077-03