基于灰色马尔可夫模型的钱塘江高潮位预测

王瑞荣，陈浩龙，薛　楚，孙映宏

(1.杭州电子科技大学生命信息与仪器工程学院，浙江 杭州 310018；2.杭州市水文水资源监测总站，浙江 杭州 310014)



基于灰色马尔可夫模型的钱塘江高潮位预测

王瑞荣1，陈浩龙1，薛楚1，孙映宏2

(1.杭州电子科技大学生命信息与仪器工程学院，浙江 杭州 310018；2.杭州市水文水资源监测总站，浙江 杭州 310014)

摘要：钱塘江高潮位符合海潮变化规律的同时，更容易受到水文、气象等因素影响.针对潮位预报难、预报精度低的问题，通过对2001—2010年钱塘江历史高潮位数据的分析和研究，将灰色系统理论与马尔可夫链结合，建立了灰色马尔可夫潮位残差修正预测模型.利用灰色预测模型对未来的潮位进行预测，并对预测结果用马尔可夫链进行修正，以提高预测精度.该模型预测了钱塘江盐官水文站2011—2012年农历八月十八的高潮位，并与实测高潮位数据和现用的预报方法进行对比，验证了灰色马尔可夫模型在钱塘江高潮位预测中具有较高的精度.

关键词：灰色系统；马尔可夫链；灰色马尔可夫模型；潮位预测

0引言

钱塘江因其喇叭形的河口和河道的泥沙淤积，当东海潮波进入杭州湾后向上游推进的过程中形成了涌潮，涌潮会引起潮位陡增现象[1].准确地预测高潮位为钱塘江水资源优化管理、航运安全管理及防潮减灾管理提供了科学的决策依据.目前，国内外学者提出的应用于海洋潮位预测的方法有调和分析法、支持向量机、混沌理论、卡尔曼滤波法等[2-5].由于钱塘江高潮位受水文、气象等不确定因素影响较大，上述方法不适合于钱塘江潮位预报.对于钱塘江的潮位预测，有传统的基于统计规律的预测方法[6]和基于BP人工神经网络的预测方法[7].前一种方法预测精度低，后一种方法存在网络的初始权值、网络结构难于确定等不足，并且随着训练次数的增加出现预测值过拟合的现象.文献[8-9]应用灰色马尔可夫模型分别对于桥水文站的水位和杭州湾风暴潮引起的极端潮位变化进行了预测，取得了较高的预报精度.钱塘江高潮位变化是受多种因素影响的复杂过程，无法准确定量地判断各种因素对高潮位的影响，故可将钱塘江高潮位视为没有物理原型、信息不完全的灰色系统，可以用灰色理论加以研究[10].本文通过对钱塘江盐官水文站历史高潮位数据的研究，寻找规律，将灰色GM(1,1)模型和马尔可夫链结合起来，建立了高潮位灰色马尔可夫预测模型，利用GM(1,1)模型预测高潮位的发展趋势，用马尔可夫链确定状态转移规律，提高了钱塘江高潮位的预测精度，为钱塘江的高潮位预测提供了一种值得探讨和实践的新途径.

1灰色马尔可夫模型

1.1GM(1,1)模型建立

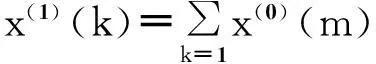
(1)

按照最小二乘法求出式(1)的结果为：

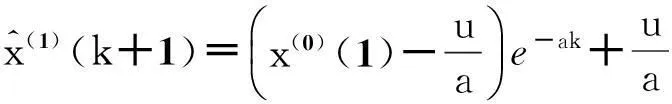
(2)

还原数列可得到预测模型为：

(3)

1.2灰色马尔可夫模型的建立

马尔可夫模型是根据事物各个状态的起始概率和状态转移规律来预测事物的发展变化，该模型准确度高、适应性强[12].变量t是固定值，函数x(t)为随机变量，在时刻t=i的状态已知，t=i+1位于的状态和ti时刻的状态有关，而和ti时刻之前的状态无关.

对于随机过程{Xn，n∈T}，若对于任意的整数n∈T和任意的状态i0,i1,…,in+1∈I，条件概率满足：

P(Xn+1=in+1|X0=i0,X1=i1,…,Xn=in)=P(Xn+1=in+1|Xn=in),

(4)

称{Xn，n∈T}为马尔可夫链.马尔可夫链的转移概率为：

pij=P(Xn+1=j|Xn=i)，

(5)

系统状态转移概率矩阵为：

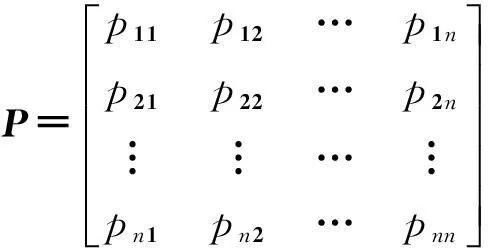
(6)

式(6)为n个状态相互转移的概率分布，pij由马尔可夫链状态si转移到sj的概率.其中0≤pij≤1，实际计算中由状态转移的频率作为状态转移的概率.状态sj出现的次数为ni，有状态si转移到sj的状态次数为nij，便有：

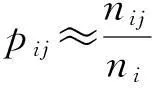
(7)

灰色马尔可夫模型预测过程如下：

1)通过高潮位实测值与灰色GM(1,1)模型预测值的残差范围确定状态的划分标准；

2)由公式s1=s0P1,s2=s0P2,…,sn=s0Pn，确定出经过n步转移后残差出现的状态，其中s0为残差初始状态概率向量，P为转移概率矩阵；

3)最后确定出残差状态概率最大的范围区间的中位数加上灰色GM(1,1)模型预测值进行修正，得到更加准确的预测结果.

2钱塘江高潮位预测实例分析

笔者以钱塘江盐官水文站2001—2012年农历八月十八高潮位数据为例(数据来源：杭州市水文水资源监测总站，数据如表1所示)，其中以2001—2010年农历八月十八的高潮位数据建立模型，并以2011—2012年同期的高潮位数据作为检验模型优劣的标准.

表1　2001—2012年农历八月十八钱塘江盐官水文站高潮位数据

2.1GM(1,1)模型求解

由表1中的数据根据1.1节中建立灰色预测模型的步骤得到GM(1,1)模型如下：

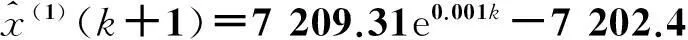
(8)

累减还原得到：

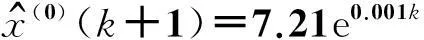
(9)

其中，a=-0.001，u=7.202 4，由式(9)得到GM(1,1)模型高潮位预测值.

2.2灰色马尔可夫模型预测

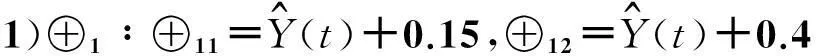
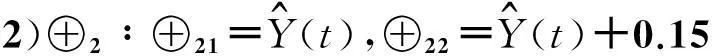
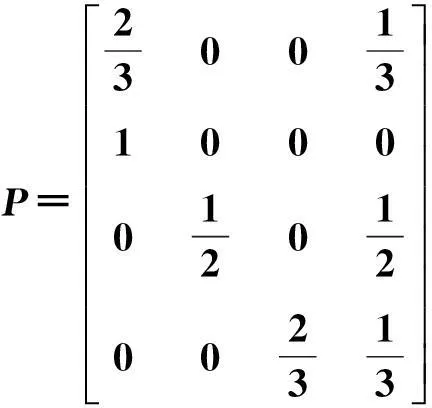
(10)

由式(10)知，4种状态的中位数分别为0.275，0.075，-0.075和-0.275，由状态转移矩阵及各个年份所处的状态，可以确定灰色马尔可夫预测值.方法如下：选取的数据2001年为初始数据，其高潮位灰色马尔可夫预测值基于灰色模型预测值.以2002年为例，因为2001年的数据处于状态4，由状态转移矩阵可知2002年的高潮位处于状态3的概率为2/3，处于状态4的概率为1/3，因此，2002年的灰色马尔可夫预测值=灰色预测值+2/3×(-0.075)+1/3×(-0.275)=7.08 m，同理可求出其它年份的高潮位的灰色马尔可夫预测值.

灰色预测模型和灰色马尔可夫模型得到的高潮位预测值、残差及相对误差绝对值如表2所示.

表2　灰色预测模型与灰色马尔可夫预测模型预测结果对比

从表2中可以看出，计算灰色GM(1,1)预测模型的平均相对误差绝对值为3.18%，灰色马尔可夫模型的平均相对误差绝对值为2.98%，改进后模型的预测误差低于灰色GM(1,1)高潮位预测模型.

两种模型对高潮位的拟合结果对比如图1所示.灰色GM(1,1)预测模型呈现一条平滑的曲线，而灰色马尔可夫模型能较好地预测出高潮位数据的波动性，精度较高.

由于表2的预测数据是在已知年份数据基础上建立的模型，对已知年份的预测准确度高，然而利用已知数据对未知数据预测并不一定准确.根据上述两种模型，再分别对钱塘江盐官2011—2012年农历八月十八的高潮位进行预测，进行进一步地检验.由表2可知，初始状态向量为s0=[0.3,0.1,0.2,0.4]，再根据马尔可夫模型s1=s0P1,s2=s0P2,…,sn=s0Pn，得到2011—2012年预测状态向量如表3所示.

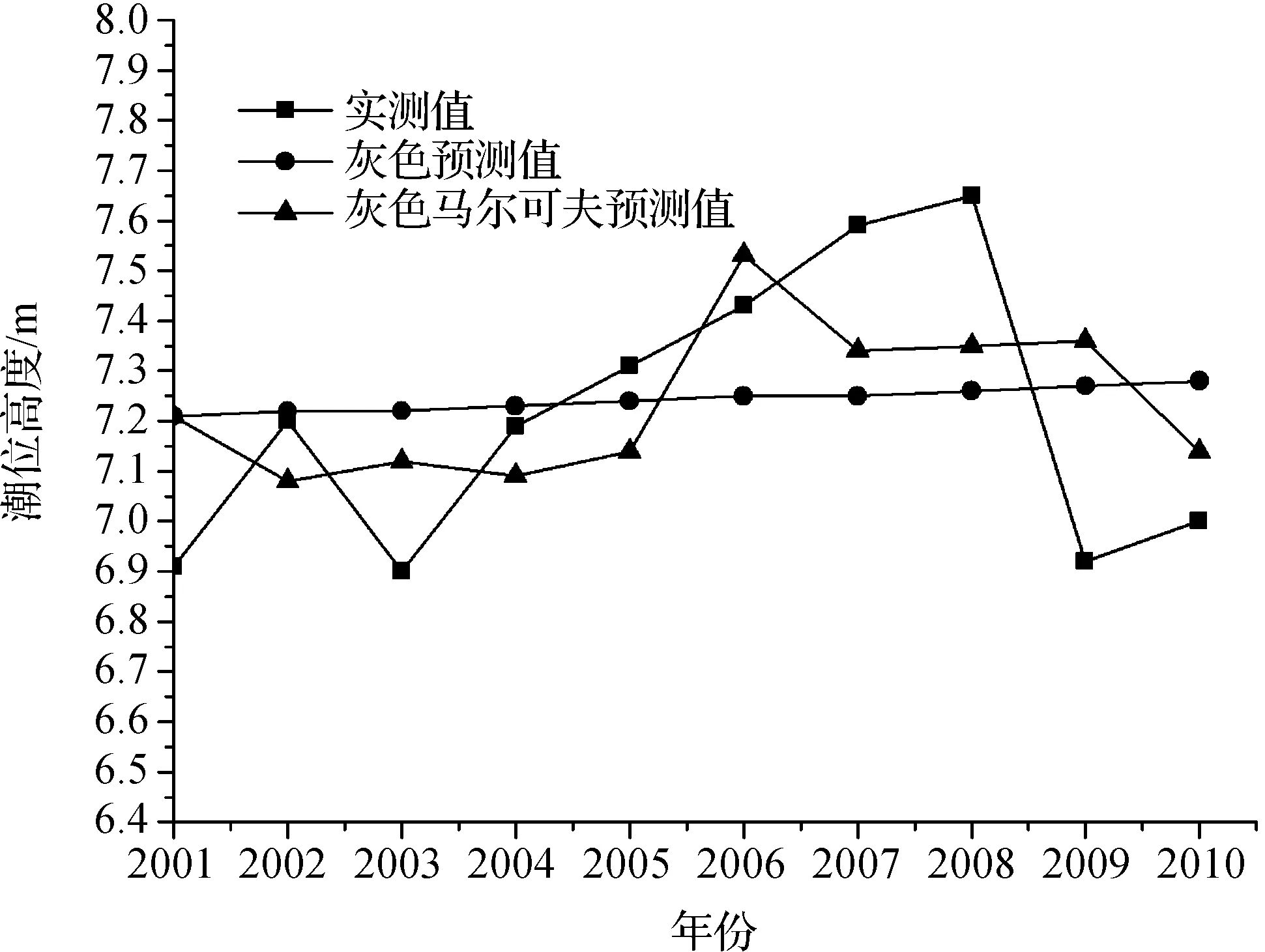
图1　两种模型拟合结果对比

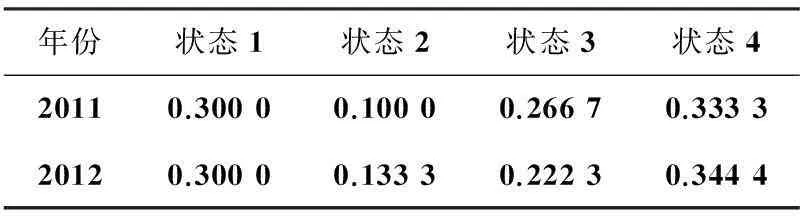
年份状态1状态2状态3状态420110.30000.10000.26670.333320120.30000.13330.22230.3444

由表3可知，2011—2012年农历八月十八的高潮位预测的残差分别处于4和4的概率最大，因此对2011—2012年农历八月十八的高潮位在灰色预测模型的基础上进行修正得到灰色马尔可夫预测值，结果如表4所示.

根据文献[13]提出的现有预报方法预测了盐官水文站2011—2012年农历八月十八的高潮位值及残差相对误差分析，分析比较结果如表4所示.结果表明，灰色马尔可夫预测模型比现有的方法在钱塘江高潮位中预测中有更高的精度.现有的预报方法选用的原始数据序列长度短、预测结果的可靠性和精度和预测步长不能满足要求.

表4　灰色预测模型、灰色马尔可夫模型与现有预测模型预测结果对比

3结束语

本文利用历史高潮位数据建立了GM(1,1)预测模型，并对残差使用了马尔可夫链修正，最终建立了灰色马尔可夫高潮位预测模型.同时，对钱塘江盐官水文站2011—2012年农历八月十八的高潮位进行了预测，并与实际潮位数据和现用预报方法比较，其结果验证了灰色马尔可夫模型预测精度高于单一的灰色预测模型和现用预报方法.目前对于钱塘江潮位预报的3种方法(人工神经网络、现用预报方法、灰色马尔可夫法)中，后两种方法简单、可操作性强，并且灰色马尔可夫法预测精度更高，为钱塘江的高潮位预测提供了全新的方法，可用于今后的实践中.

参考文献

[1]潘存鸿,鲁海燕,曾剑.钱塘江涌潮特性及其数值模拟[J].水利水运工程学报,2008(2):1-9.

[2]张凤烨,魏泽勋,王新怡,等.潮汐调和分析方法的探讨[J].海洋科学,2011,35(6):68-75.

[3]HESJ,ZHOUWJ,ZHOURY,etal.Studyoftidepredictionmethodinfluencedbynonperiodicfactorsbasedonsupportvectormachines[J].ActaOceanologicaSinica,2012,31(5):160-164.

[4]SANNASIRAJSA,ZHANGH,BABOVICV,etal.Enhancingtidalpredictionaccuracyinadeterministicmodelusingchaostheory[J].AdvancesinWaterResources,2004,27(7):761-772.

[5]YENPH,JANCD,LEEYP,etal.ApplicationofKalmanfiltertoshort-termtidelevelprediction[J].JournalofWaterway,Port,Coastal,andOceanEngineering,1996,122(5):226-231.

[6]周黔生.钱塘江涌潮简析与预报[J].水文,1994(6):12-16.

[7]何峰,王瑞荣,王建中,等.一种基于BP神经网络的江河潮位短期预测[J].长江科学院院报,2011,28(1):21-24.

[8]DONGS,CHIK,ZHANGQ,Yetal.TheapplicationofaGreyMarkovModeltoforecastingannualmaximumwaterlevelsathydrologicalstations[J].JournalofOceanUniversityofChina,2012,11(1):13-17.

[9]刘德辅,姜昊.台风诱发暴潮极端潮位的预测方法[J].中国海洋大学学报(自然科学版),2009,39(3):516-520.

[10]DENGJL.Controlproblemsofgreysystems[J].SystemsandControlLetters,1982,1(5):288-294.

[11]刘思峰,杨英杰,吴利丰,等.灰色系统理论及其应用[M].北京:科学出版社,2014:140-146.

[12]臧文亚,周仲礼,龚灏,等.基于灰色马尔科夫模型的重庆市水运货运量的预测[J].水运工程,2012(1):30-33.

[13]徐翠飞.基于数据和黑箱建模理论的钱塘江涌潮自动检测与实时预报方法[D].杭州:杭州电子科技大学,2014．

Prediction on Qiantang River’s High Tidal Level Based on Grey Markov Model

WANG Ruirong1, CHEN Haolong1, XUE Chu1, SUN Yinghong2

(1.SchoolofLifeInformation&InstrumentEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China;2.HangzhouHydrologyandWaterResourcesMonitoringStation,HangzhouZhejiang310014,China)

Abstract：The tidal level of Qiantang River has the same feature as the tidal level of ocean, but the former is more easily affected by hydrology and meteorology. To deal with difficulty and low accuracy in prediction of the tidal level of river, according to the study and analysis of hydrological data of Qiantang River from 2001 to 2010, with low accuracy using GM(1,1) model to the high tidal level, grey-Markov model is established to predict the Qiantang River’s tidal level by combining the grey model with Markov chain. In order to improve the accuracy, the grey model predicts the tidal level, and the prediction results are corrected by Markov chain. The model predicts the high tidal level of august eighteenth of Lunar calendar and tendency of a month in YanGuan hydrographic station from 2011—2012. Based on the practical prediction, the prediction accuracy of this model is significantly higher than that of grey prediction model and prediction method of using.

Key words：grey system; Markov chain; grey-Markov model; tidal level prediction

DOI：10.13954/j.cnki.hdu.2016.02.012

收稿日期：2015-07-29

基金项目：国家自然科学基金资助项目(61374005)；浙江省自然科学基金资助项目(LY14F030022)

作者简介：王瑞荣(1973-)，男，浙江义乌人，教授，钱塘江潮汐检测和预报.

中图分类号：P33

文献标识码：A

文章编号：1001-9146(2016)02-0057-05