一类3值逻辑2元Sheffer函数
杜 国 平
一类3值逻辑2元Sheffer函数
杜 国 平
【摘要】3值逻辑Sheffer函数研究是多值逻辑重要的基础理论之一。通过给出严格的相互可定义性,54个3值2元S型函数可分为相互定义的10个组,并且可分为3种类型:117型、135型和333型。其中,117型6个,135型36个,333型12个。通过严格的定义可以证明:只有333型中的6个不是Sheffer函数,其余48个均为Sheffer函数。在此基础上,可以进一步发现并证明大量的其他类Ci型和类Di 型Sheffer函数。
【关键词】3值逻辑Sheffer函数S型函数类Ci型Sheffer函数
一、3值2元Sheffe函数的类型
3值逻辑Sheffer函数研究是多值逻辑重要的基础理论之一。*Lou Goble. The Blackwell Guide to Philosophical Logic, Wiley-Blackwell, 2001.本文不讨论一般的多值逻辑函数集中的准完备集问题,而是通过给出严格的相互可定义性来分析某些特殊函数之间的关系,并证明相关结果。n值m元逻辑函数共有nnm个,3值2元逻辑函数共计有332,即19 683个,将近两万个。如果对所有这些函数一个一个地讨论其是否是Sheffer函数,那将是一项艰苦而繁琐的工作。因此我们将选择其中的一类特殊函数对其进行分析、归类。
取E3={0, 1, 2},一个3值2元逻辑函数G(x,y)的真值表是如下的一个九宫格:
一个3值2元Sheffer函数的真值表其V1位置上不可能是0。因为如果这个位置是0,意味着G(0,0)=0,因此G(x,y)就不可能定义出3值一元函数~x:
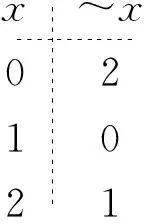
同样,一个3值2元Sheffer函数的真值表其V5位置上不可能是1,V9位置上也不可能是2。一个3值2元逻辑函数G(x,y)如果是Sheffer函数,那么其真值表可能是如下情形之一。
一个3值2元Sheffer函数要能定义出所有的3值逻辑函数,当然包括诸如max(x,y)、min(x,y)这样的逻辑函数,考虑到max(x,y)和min(x,y)的真值表其中的变元具有对称性(即在真值表中,V2和V4、V3和V7、V6和V8位置上的值相同),因此下面我们研究这类真值表中的变元具有对称性的3值2元函数。*杜国平:《单独函数完全的算子》,载《哲学研究》2000年第6期。这样的函数共有54个(我们称之为3值2元S型函数),其真值表如下。
……
……
已经证明,其中的D4,D5,D7,D23,D25,D26,C10,C13,C15,C19,C21,C24等12个是3值2元Sheffer函数。*杜国平:《三值逻辑Sheffer函数》,载《哲学动态(逻辑学研究专辑)》2005年。

那么,由上述结果可得:

容易证明:
[1]D14pq=C1C1pqC1pq
[2]D1pq=C1C1ppC1qq
[3]C1pq=D1D1pqD1pq
[4]C1pq=D1D1ppD1qq
[5]C1pq=D14D14pqD14pq
[6]C14pq=D14D14ppD14qq
[7]D1pq=C14C14pqC14pq
[8]D27pq=C14C14ppC14qq
[9]C14pq=D27D27pqD27pq
[10]C27pq=D27D27ppD27qq
[11]D27pq=C27C27ppC27qq
[12]D1pq=C27C27pqC27pq


















这样,C1、C14、C27、D1、D14和D27构成了可以相互定义的一个组。
容易证明:
[13]D15pq=C2C2pqC2pq
[14]D10pq=C2C2ppC2qq
[15]C2pq=D15D15pqD15pq
[16]C17pq=D15D15ppD15qq
[17]C9pq=D10D10pqD10pq
[18]C2pq=D10D10ppD10qq
[19]D21pq=C17C17pqC17pq
[20]D15pq=C17C17ppC17qq
[21]C17pq=D21D21pqD21pq
[22]C9pq=D21D21ppD21qq
[23]D10pq=C9C9pqC9pq
[24]D21pq=C9C9ppC9qq







这样,C2、C9、C17、D10、D15和D21构成了可以相互定义的一个组。
容易证明:
[25]D13pq=C3C3pqC3pq
[26]D19pq=C3C3ppC3qq
[27]C3pq=D13D13pqD13pq
[28]C11pq=D13D13ppD13qq
[29]C18pq=D19D19pqD19pq
[30]C3pq=D19D19ppD19qq
[31]D24pq=C11C11pqC11pq
[32]D13pq=C11C11ppC11qq
[33]C11pq=D24D24pqD24pq
[34]C18pq=D24D24ppD24qq
[35]D19pq=C18C18pqC18pq
[36]D24pq=C18C18ppC18qq







这样,C3、C11、C18、D13、D19和D24构成了可以相互定义的一个组。
容易证明:
[37]D17pq=C4C4pqC4pq
[38]D2pq=C4C4ppC4qq
[39]C25pq=D2D2pqD2pq
[40]C4pq=D2D2ppD2qq
[41]C4pq=D17D17pqD17pq
[42]C23pq=D17D17ppD17qq
[43]D9pq=C23C23pqC23pq
[44]D17pq=C23C23ppC23qq
[45]C23pq=D9D9pqD9pq
[46]C25pq=D9D9ppD9qq
[47]D2pq=C25C25pqC25pq
[48]D9pq=C25C25ppC25qq







这样,C4、C23、C25、D2、D9和D17构成了可以相互定义的一个组。
容易证明:
[49]D18pq=C5C5pqC5pq
[50]D11pq=C5C5ppC5qq
[51]C7pq=D11D11pqD11pq
[52]C5pq=D11D11ppD11qq
[53]C5pq=D18D18pqD18pq
[54]C26pq=D18D18ppD18qq
[55]D11pq=C7C7pqC7pq
[56]D3pq=C7C7ppC7qq
[57]C26pq=D3D3pqD3pq
[58]C7pq=D3D3ppD3qq
[59]D3pq=C26C26pqC26pq
[60]D18pq=C26C26ppC26qq







这样,C5、C7、C26、D3、D11和D18构成了可以相互定义的一个组。
容易证明:
[61]D16pq=C6C6pqC6pq
[62]D20pq=C6C6ppC6qq
[63]C6pq=D16D16pqD16pq
[64]C20pq=D16D16ppD16qq
[65]C16pq=D20D20pqD20pq
[66]C6pq=D20D20ppD20qq
[67]D20pq=C16C16pqC16pq
[68]D6pq=C16C16ppC16qq
[69]C20pq=D6D6pqD6pq
[70]C16pq=D6D6ppD6qq
[71]D6pq=C20C20pqC20pq
[72]D16pq=C20C20ppC20qq







这样,C6、C16、C20、D6、D16和D20构成了可以相互定义的一个组。
容易证明:
[73]D12pq=C8C8pqC8pq
[74]D12pq=C8C8ppC8qq
[75]C8pq=D12D12pqD12pq
[76]C8pq=D12D12ppD12qq



这样,C8和D12构成了可以相互定义的一个组。
容易证明:
[77]C12pq=D22D22pqD22pq
[78]C12pq=D22D22ppD22qq
[79]D22pq=C12C12pqC12pq
[80]D22pq=C12C12ppC12qq



这样,C12和D22构成了可以相互定义的一个组。
容易证明:
[81]C22pq=D8D8pqD8pq
[82]C22pq=D8D8ppD8qq
[83]D8pq=C22C22pqC22pq
[84]D8pq=C22C22ppC22qq



这样,C22和D8构成了可以相互定义的一个组。
通过上述研究,可以看出54个3值2元逻辑函数可以分为内部可以相互定义的10组:










我们可以按其首元分别将其称之为C1组、C2组等等。按照真值表中3个值的个数不同,又可以将54个3值2元逻辑函数分为3种类型:117型(即真值表中3个值的数目分别为1个、1个和7个)、135型和333型。其中117型只有C1组;333型包括C6组、C8组、C12组和C22组;其余5组均为135型。
二、3值2元逻辑函数的表达能力
上述54个3值2元逻辑函数共分成了10种类型,这10种类型之中的函数是相互可定义的,那么它们的表达能力是相同的。下面我们来研究这10种类型之间的可表达性。当然,首先我们已经知道下述12个Sheffer函数其表达能力是最强的:

下面讨论其他类型之间的可表达性。

[1]E1pq=C2D10pqD15pq
[2]C5pq=C2E1pqE1pq
[3]E2pq=C2D10pqD21pq
[4]C26pq=C2E2pqE2pq
[5]E3pq=C2D15pqD21pq
[6]C23pq=C2E3pqE3pq
[7]E4pq=C9D10pqD15pq
[8]C4pq=C9E4pqE4pq
[9]E5pq=C9D10pqD21pq
[10]C7pq=C9E5pqE5pq
[11]E1pq=C9D15pqD21pq
[12]C5pq=C9E1pqE1pq
[13]E5pq=C17D10pqD15pq
[14]C7pq=C17E5pqE5pq
[15]E6pq=C17D10pqD21pq
[16]C25pq=C17E6pqE6pq
[17]E2pq=C17D15pqD21pq
[18]C26pq=C17E2pqE2pq



下面进一步使用已经获得定义的逻辑函数来考察C2组的表达能力:
[19]C11pq=C2E1pqE2pq
[20]C14pq=C2E1pqE3pq
[21]C4pq=C2E1pqE4pq
[22]C1pq=C2E1pqE5pq
[23]C10pq=C2E1pqE6pq
[24]C20pq=C2E2pqE3pq
[25]C10pq=C2E2pqE4pq
[26]C16pq=C2E2pqE5pq
[27]C25pq=C2E2pqE6pq
[28]C13pq=C2E3pqE4pq
[29]C10pq=C2E3pqE5pq
[30]C19pq=C2E3pqE6pq
[31]C1pq=C2E4pqE5pq
[32]C10pq=C2E4pqE6pq
[33]C16pq=C2E5pqE6pq




更为关键的是,由[23][25][29][30]和[32]可以看出C2组可以定义出Sheffer函数C10和C19,因此可以得出C2、C9、C17、D10、D15和D21都是Sheffer函数。

[34]F1pq=C3D13pqD19pq
[35]C6pq=C3F1pqF1pq
[36]F2pq=C3D13pqD24pq
[37]C2pq=C3F2pqF2pq
[38]F3pq=C3D19pqD24pq
[39]C14pq=C3F3pqF3pq



更为关键的是,由[37]可以看出C3组可以定义出Sheffer函数C2,因此可以得出C3、C11、C18、D13、D19和D24都是Sheffer函数。

[40]G1pq=C4D2pqD9pq
[41]C26pq=C4G1pqG1pq
[42]G2pq=C4D2pqD17pq
[43]C16pq=C4G2pqG2pq
[44]G3pq=C4D9pqD17pq
[45]C14pq=C4G3pqG3pq




下面进一步使用已经获得定义的逻辑函数来考察C4组的表达能力:
[46]C8pq=C4G1pqG2pq
[47]C2pq=C4G1pqG3pq
[48]C11pq=C4G2pqG3pq


[49]H1pq=C5D3pqD11pq
[50]C18pq=C5H1pqH1pq
[51]H2pq=C5D3pqD18pq
[52]C17pq=C5H2pqH2pq
[53]H3pq=C5D11pqD18pq
[54]C9pq=C5H3pqH3pq
由[50][52]和[54]可以看出C5组可以定义出Sheffer函数C9、C17和C18,因此可以得出C5、C7、C26、D3、D11和D18都是Sheffer函数。

[55]J1pq=C6D6pqD16pq
[56]C12pq=C6J1pqJ1pq

[57]J2pq=C6D6pqD22pq
[58]C21pq=C6J2pqJ2pq
由[58]可以看出C6组可以定义出Sheffer函数C21,因此可以得出C6、C16、C20、D6、D16和D20都是Sheffer函数。

[59]0=C1C1pqD14pq
[60]M1pq=C1p0
[61]M2pq=C10p
[62]M3pq=C1M1pqM2pq
[63]M4pq=D14D14pqD14pq
[64]M5pq=D14M3pqM3pq
[65]D2pq=C1M4pqM5pq

而前文已经证明D2是Sheffer函数,因此可以得出C1、C14、C27、D1、D14和D27都是Sheffer函数。
三、几个主要结论
定理1333型中的C8组、C12组和C22组,即C8、C12、C22、D8、D12和D22均不是Sheffer函数。
下面予以证明。
由C8的真值表不难验证:
ΘΘC8pq=C8ΘΘpΘΘq
ΘΘC12pq=C12ΘΘpΘΘq
ΘΘC22pq=C22ΘΘpΘΘq*Θ的定义见杜国平:《三值逻辑Sheffer函数》,载《哲学动态(逻辑学研究专辑)》2005年。
由此可见,C8、C12和C22是自对偶函数。*朱梧槚、肖奚安:《数理逻辑引论》,第51—62页,大连理工大学出版社2008年版。所以,C8、C12和C22不是Sheffer函数。
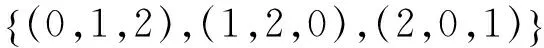
由此可得:D8、D12和D22也均不是Sheffer函数。
定理2上述54个3值2元逻辑函数均可以定义出3值1元逻辑函数Θ。
下面予以证明。
Θp=edfCiCippCipp(i=1,…,27)
Θp=edfDipp(i=1,…,27)
前述我们研究的54个函数都是其真值表中的变元具有可交换性的3值2元函数,那么是否存在其真值表中的变元不具有可交换性的3值2元Sheffer函数呢?答案是肯定的。
定理3除上述48个Sheffer函数外,还存在其他3值2元Sheffer函数。
下面予以证明。
可以定义出函数D11:

因为:
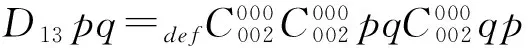
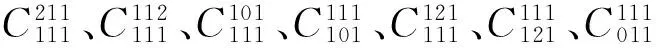
下面予以证明。
容易验证:

类似地有:

下面予以证明。
容易验证:


下面予以证明。
容易验证:

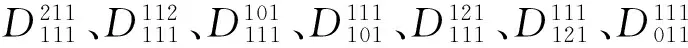
下面予以证明。
容易验证:
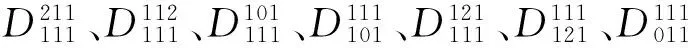

下面予以证明。
容易验证:

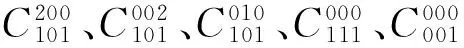
下面予以证明。
容易验证:

按照如上方法,我们还可以进一步得出其他类Ci和类DiSheffer函数。
【责任编辑:赵小华】
【基金项目】国家社会科学基金重点项目“提高国民逻辑素质的理论和实践探索研究”(13AZX019);国家社会科学基金重大招标项目“应用逻辑与逻辑应用研究”(14ZDB014)
【收稿日期】2015-10-29
【中图分类号】B81-0
【文献标识码】A
【文章编号】1000-5455(2016)01-0169-07
(作者简介:杜国平,江苏盱眙人,中国社会科学院哲学研究所教授、博士生导师。)

