薄壁方管结构在爆炸荷载作用下动力响应及破坏模式分析

宋克健， 龙　源， 纪　冲， 高福银， 李兴华

(解放军理工大学 野战工程学院，南京　210007)

薄壁方管结构在爆炸荷载作用下动力响应及破坏模式分析

宋克健， 龙源， 纪冲， 高福银， 李兴华

(解放军理工大学 野战工程学院，南京210007)

摘要：采用数值模拟与实验相结合的方法研究了薄壁方管结构在爆炸荷载作用下的动力响应。将壁厚3 mm、截面边长为100 mm的薄壁方管结构置于200 g TNT产生的爆炸场中进行冲击实验，实验表明当装药距离大于等于14 cm时，结构仅呈现局部凹陷变形，当装药距离为10 cm和12 cm时，结构除局部凹陷变形外，还呈现出整体变形模式，同时，方管迎爆面两侧边产生长条状破裂损伤。利用动力有限元程序LS-DYNA及流固耦合算法对薄壁方管变形及破坏过程进行数值模拟，得到了结构关键单元处压力分布、挠度时间曲线等参数。同时分析了结构宽厚比对试件动力响应的影响，结果表明迎爆面变形量随着宽厚比的减小而减小。

关键词：薄壁方管；爆炸荷载；动力响应；破坏模式

薄壁结构具有刚度大、质量轻、成本低、易于加工和优异的吸能特性等，广泛应用于化工、能源、航空航天等领域，研究其受爆炸荷载作用下的瞬态响应具有重要的军事和民用背景，也引起越来越多的学者的重视。Jones[1]对理想刚塑性薄壁结构受冲击荷载作用下的塑性变形进行了试验和理论研究；Wegener等[2]对简支薄壁方管受冲击荷载作用下的永久变形进行预测分析；Bambach[3]对铝合金方管受到爆炸冲击荷载作用下的局部和整体变形进行试验研究，并根据试验结果得到了计算变形的经验公式；Jama等[4]对三种不同尺寸的方管受爆炸荷载作用下的动力响应进行了理论和试验研究，并推导了方管整体变形和局部变形过程中的吸能公式。国内关于薄壁结构的研究大多集中薄壁圆柱壳体在冲击荷载作用下的动力响应研究[5-8]，而对于薄壁方管的动力响应问题涉及较少。

在前人工作的基础上，本文拟进行薄壁方管结构受到侧向爆炸荷载作用下动力响应的实验与数值模拟研究，以获得薄壁方管在不同爆炸荷载作用下的变形破坏模式。首先进行了薄壁方管结构受爆炸荷载作用的实验研究，通过调整炸药到管壁的距离，得到方管在不同荷载作用下的变形形态；进而运用有限元方法，建立数值计算模型，对薄壁方管受爆炸荷载作用的变形过程及破坏形态进行数值计算，通过数值模拟和实验结果的比较分析，获得影响薄壁结构变形形态的因素，为结构的抗爆性和变形失效模式的提供参考。

1实验研究

1.1实验设置

实验试件为Q235钢质薄壁方管，轴向长度为1.0 m，壁厚为3.0 mm，横截面外径为100 mm；以200 g压装TNT装药为爆炸源，装药尺寸为10 cm×5 cm×2.5 cm，爆炸冲击实验现场布设如图1所示，其中R为装药距离，实验主要通过调整不同装药距离，获得不同爆炸载荷作用下薄壁方管的变形模式。

图1　实验设置示意图Fig.1 Sketches of experimental layout

实验在野外靶场进行，实验前首先需要平整场地，固定两端支架，使其保持水平，然后将方管固定放置于支架上，装药悬挂于装药正上方，采用电雷管对装药进行中心起爆。通过调整装药距离，得到不同强度冲击荷载作用下方管变形形态及变形参数值。共进行了6组不同工况下的爆炸实验，装药距离分别为10 cm、12 cm、14 cm、16 cm、18 cm和20 cm，实验结果和测量参数如表1所示，其中d为方管迎爆面中心点处最大挠度，r1为方管凹陷区宽度，r2为凹陷区轴向长度，变形参数如图2所示。

图2　变形参数说明Fig.2 Sketches of the deformation parameters

1.2实验结果分析

6种不同工况下实验结果数据如表1所示。

薄壁方管结构件在爆炸冲击荷载作用下会产生整体变形和局部变形。整体变形是指结构整体产生弯曲，其测量值可以取为试件底部从初始位置到最终变形位置之间的变形量，如图3(a)所示。局部变形是指结构横截面产生局部凹陷，其值可表示为从横截面顶部初始位置最终位置之间的变形量，如图3(b)所示。

表1　薄壁方管受爆炸荷载的冲击变形模态

图3　方管试件整体变形和局部变形示意图Fig.3 Sketches of global and local deformation of square tubes

图4给出了薄壁方管结构在不同工况下受爆炸载荷作用下的变形模态。从图4和表1等实验结果可以看出，当薄壁方管受到爆炸荷载作用时，方管迎爆面壳壁会产生不同程度的内凹屈曲变形，中心点处变形挠度最大，由中心点向四周变形挠度依次减小，方管迎爆面两侧边在爆炸荷载作用下会发生向内弯折变形。当装药距离较大时，薄壁方管迎爆面各点处变形量均较小，随着装药距离的减小，迎爆面中心点的挠度逐渐增大，凹陷区宽度逐渐减小。当装药距离减小到12 cm时，方管迎爆面两侧边在强爆炸荷载作用下产生冲击损伤，在中心部位处形成了破裂缺口，缺口长度为4.2 cm，最大宽度为0.8 cm。随着装药距离继续减小，方管破裂缺口和损伤面积持续增大，当装药距离减小到10 cm时，缺口长度达到6.4 cm，最大宽度为2.2 cm。由此表明，薄壁方管迎爆面两侧边处最容易受到冲击损伤破坏，在进行工程防护及结构设计时应重点关注。由实验结果还可以看到，当装药距离较大时，薄壁方管结构仅发生局部变形而没有整体变形，随着装药距离的减小，结构整体变形逐渐增大。

图4　薄壁方管冲击变形模态Fig.4 Deformation modes of thin-walled steel square tubes

2数值模拟

为了深入研究结构在爆炸荷载作用下的动力响应过程及失效特性，采用LS-DYNA有限元程序对薄壁方管结构受侧向爆炸荷载作用过程进行数值模拟研究。

2.1数值计算模型及边界处理

图5所示为数值模拟的1/2有限元模型。根据爆轰产物与结构相互作用问题的特性，采用多物质ALE算法，即将气体爆轰产物、空气等与薄壁方管等固体结构的相互作用进行耦合计算。定义炸药、空气为Euler网格，方管结构为Lagrange网格，将空气侧面定义为透射边界。采用SOLID164六面实体单元划分网格，对称面上的节点设置对称约束，并采用cm-g-μs单位制。

图5　有限元计算模型Fig.5 The finite element model

2.2材料模型及参数

TNT装药采用高能炸药模型，爆轰产物的膨胀采用JWL状态方程来描述[9]，并假定爆轰前以常速度传播。以炸药爆轰产物的压力p表示的状态方程为：

(1)

式中：η=ρ/ρc，ρ为爆轰产物密度；A1、B1、R1、R2、ω为实验拟合参数。计算中，TNT炸药C-J参数和JWL状态方程参数为：炸药密度ρe=1.60 g/cm3，爆速D=6.93 km/s，爆轰波阵面压力pcj=21.0 GPa，单位体积炸药内能E0=7.0×109J/m3，A1=371.2 GPa，B1=3.231 GPa；R1=4.15，R2=0.95；ω=0.30。

空气采用空白材料模型(NULL)。空气的状态方程采用理想气体状态为p=(γ-1)ρe0/ρ0。其中空气初始密度ρ0=1.29×10-3g/cm3，绝热指数γ=1.4，气体比内能e0=0.25 MPa。

薄壁方管材料采用Johnson-Cook模型[10]。对Von Mises屈服应力模型，材料屈服应力表示为：

(2)

(3)

式中：σ*=p/σe，p为压力，σe为Von Mises等效应力。当损伤参数D=∑Δε/εf值为1.0时，断裂发生。其中Δε为积分循环期间的等效塑性应变增量。Q235钢的材料模型参数见参考文献 [10]。

3数值计算结果及分析

3.1壳体局部凹陷变形过程及结果分析

图6所示为薄壁方管结构在装药距离R为14 cm的侧向爆炸冲击荷载作用下的变形过程。由图可知，装药在结构中心正上方起爆后32 μs时，爆轰产物及冲击波开始作用到薄壁方管的迎爆面上。当壳体迎爆面所受到的作用力大于壳体材料的极限静止压力，迎爆面中心点处会产生塑性变形。当t=56 μs时，方管结构迎爆面两直角边受冲击载荷作用，开始产生变形，随着爆轰产物及冲击波的持续作用，塑性变形区面积逐渐增大，当t=124 μs时，迎爆面侧壁发生明显向内弯折，且随着时间变化，变形量逐渐增大。薄壁方管的塑性变形可以简化为三塑性铰模型：其中一个塑性铰位于方管迎爆面中心点处，另外两个塑性铰位于迎爆面两侧壁位置处，方管的塑性变形即壳体在塑性铰处发生转动所致。

图6　方管的变形过程Fig.6 Deformation of the square tubes

爆炸荷载作用下方管迎爆面中心点相关参数能准确反映变形过程，通过数值模拟计算可以得到不同装药距离下薄壁方管迎爆面中心点处挠度变化曲线以及压力变化曲线，如图7、图8所示，由图7可以看出，不同装药距离下薄壁方管迎爆面中心点挠度均首先急剧增大，然后逐渐趋于平稳。当装药距离为20 cm时，方管迎爆面中心点处挠度最小，为5.12 cm；随着装药距离的减小，方管迎爆面中心点处挠度值逐渐增大，当装药距离为10 cm时，中心点处挠度值为9.65 cm。图8所示为装药距离分别为10 cm、16 cm和20 cm时薄壁方管迎爆面中心点处压力-时间曲线，其峰值超压分别为18.8 MPa、13.33 MPa和9.13 MPa。装药空气中爆炸产生的冲击波超压可采用亨利奇公式[11]进行验算：

(4)

图7 不同装药距离下方管中心点挠度-时间曲线Fig.7Deflectionversustimecurveofmiddlepointatdifferentchargedistance图8 不同装药距离下方管中心点压力-时间曲线Fig.8Pressureversustimecurveofmiddlepointatdifferentchargedistance图9 不同装药距离下冲击波超压理论与数值模拟对比曲线Fig.9Comparisionofpeakpressurebetweennumericalsimulationandtheoreticalcalculation

为研究薄壁方管表面不同位置处的位移和压力分布规律，选取薄壁方管迎爆面上若干关键节点进行分析。其中节点A为方管迎爆面中心点位置，节点B、C、D、E位于迎爆面中心轴线上，各节点之间间距5 cm，节点F、G位于迎爆面中面径向位置处，距离节点A分别为2 cm和5 cm，节点位置示意图如图10所示。

图10　节点选取示意图(cm)Fig.10 Sketches of node selection(cm)

图11(a)、11(b)分别给出了轴向及径向各节点处的挠度-时间曲线。图中可以看出，薄壁方管迎爆面中心点A处变形挠度值在所有节点中最大，其余各节点随到A点距离的增大，变形挠度逐渐减小。从图中还可以看出，节点A处变形速率先增大，后逐渐减小，而随着距离的增大，节点D、E处变形速率则一直较小，节点E处的挠度-时间曲线近似为直线。图12(a)、12(b)分别给出了各节点处的压力-时间曲线，由图所示，节点A处的峰值压力最大，各节点随着到A点距离的增大，峰值压力急剧降低。

图11　各节点处挠度-时间曲线Fig.11 Deflection-time curve of different nodes

图12　各节点处压力-时间曲线Fig.12 Pressure-time curve of different nodes

薄壁方管结构迎爆面中心点位移的数值计算结果与实验结果对比如图13所示。通过对比可以看出，数值模拟结果与实测数据具有良好的一致性。图14所示为装药距离14 cm时，数值模拟与试验的最终变形模态对比，数值模拟结果与试验吻合较好，表明本文数值模拟模型和参数选取合理，结果可信，可以用于薄壁方管的塑性变形分析。

图13　方管迎爆面中心点变形挠度实验与数值模拟结果比较Fig.13 Comparison of central point deflection between numerical and experimental results

图14　变形模态数值模拟与实验对比Fig.14 Numerical deformation compared with experimental deformation

3.2薄壁方管破裂响应分析

通过现场试验可知，当装药距离较小时，薄壁方管结构迎爆面壳壁产生较大的塑性变形。当壳壁材料的塑性应变超过极限断裂强度时，会在壳壁处产生裂纹，随着裂纹的扩展，逐渐形成破裂口。选取装药距离为10 cm，通过数值模拟验证此变形过程，如图15所示。

图15　方管破裂损伤数值模拟Fig.15 Numerical simulation of square tubes’ damage process

图16　方管破裂数值模拟与实验对比Fig.16 Comparison between numerical damage deformation and experimental result

由图15可以看出，装药被引爆后24 μs，爆轰产物开始作用到薄壁方管迎爆面上，当t=110 μs时，迎爆面中心点两端产生初始裂缝，裂缝沿方管轴向向两端扩展。随着爆轰产物作用的进一步作用，裂缝长度和宽度逐渐增大，形成长条形破裂缺口。数值模拟结果与实验结果的对比如图16所示，由图可知，数值模拟结果与实验吻合较好，表明所选取的材料模型及数值模拟方法可用于薄壁方管的破裂损伤分析，结果可信度较高。

3.3结构宽厚比对试件破坏及动态响应的影响

从3.1和3.2节的分析可以看出，装药距离对薄壁方管结构的动力响应及破坏模式影响较大。此外，试件的材料强度、外形尺寸等因素对结果也有较大的影响。本节采用上述数值模拟方法，对薄壁结构的宽厚比对试件破坏及动态响应的影响进行分析。数值模拟分析采取固定结构宽度、调整壁厚的方法来调节宽厚比。方管结构宽度w固定为10 cm，壁厚t分别为2 mm、2.5 mm、3 mm、4 mm和5 mm等，从而得到结构宽厚比w/t分别为50、40、33.3、25和20。5种不同宽厚比条件下方管迎爆面中心点位移时间曲线如图17所示。

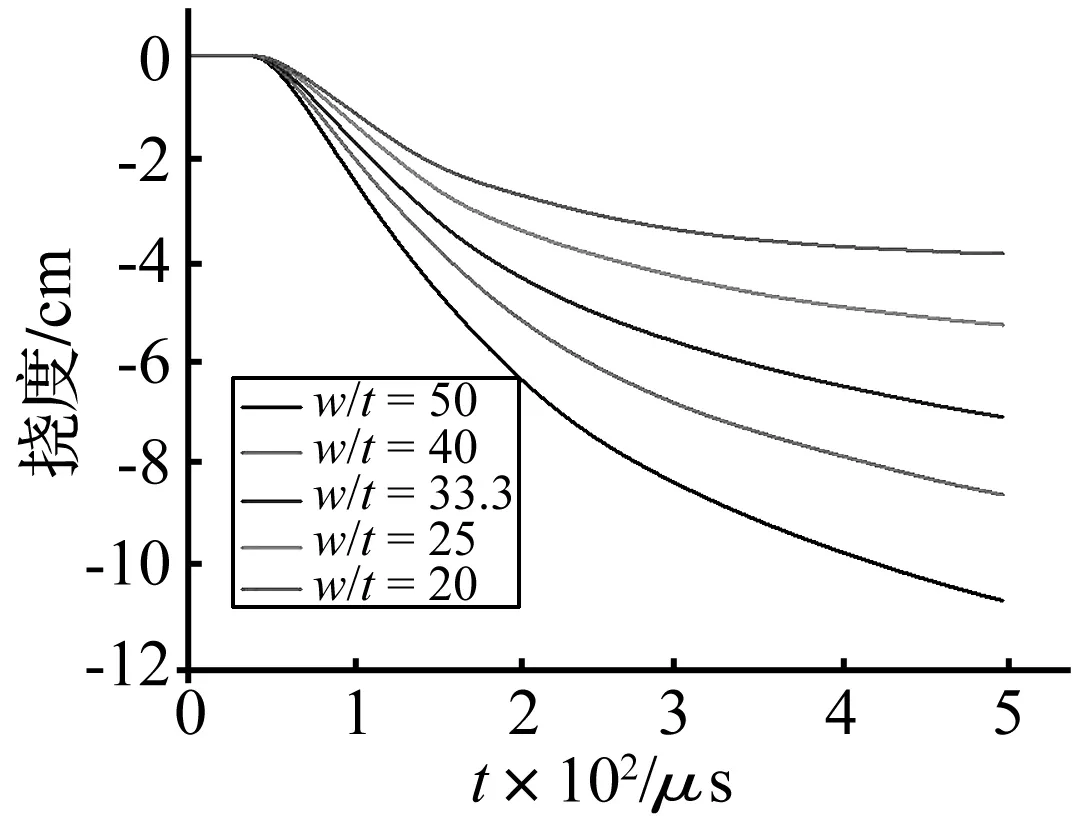
图17　不同宽厚比条件下结构中心点挠度-时间曲线Fig.17 Deflection-time curves of central points at different width to thickness ratio

从图中可以看出，方管迎爆面中心点垂直方向位移在宽厚比为50(壁厚为2 mm)时最大，达到10.64 cm。随着宽厚比的减小，迎爆面中心点位移也逐渐减小。当宽厚比为20(壁厚为5 mm)时，垂直方向位移为3.86 cm。实际上，宽厚比的减小表示结构横截面“变厚”，可以承受更大的载荷作用。在相同荷载作用下，宽厚比较大的方管结构更容易产生塑性变形。

4结论

(1) 薄壁方管在200 g压装TNT装药产生的爆炸场中的冲击实验表明：薄壁方管在不同载荷强度下呈现出不同的变形模态，当装药距离大于等于14 cm时，结构仅发生局部凹陷变形，当装药距离小于14 cm时，结构开始产生整体变形，随着装药距离的进一步减小，结构迎爆面甚至产生冲击损伤；

(2) 当装药距离为10 cm和12 cm时，薄壁方管迎爆面侧边均产生冲击损伤，损伤部位形状呈长条形缺口，当装药距离为12 cm时，缺口长度和宽度分别为4.2 cm和0.8 cm，当装药距离为10 cm时，缺口长度和宽度分别为6.4 cm和2.2 cm，通过研究还可以看出，薄壁方管迎爆面两侧边部位最易产生冲击损伤，在进行结构设计和工程防护计算时应增强此部位的防冲击性能；

(3) 通过数值模拟的方法研究了方管结构的宽厚比对试件破坏及动态响应的影响，研究表明，方管迎爆面变形量随着宽厚比的减小而减小；

(4) 论文采用的数值模拟方法能准确模拟载荷在薄壁方管迎爆面上的分布规律，结构变形模态及参数与实验结果比较误差在工程允许的范围内，为薄壁方管结构的抗爆及安全性评估提供分析依据。

参 考 文 献

[1] Jones N. Structural impact[M]. Cambridge, UK: Cambridge University Press, 1997.

[2] Wegener R B, Martin J B. Predictions of permanent deformation of impulsively loaded simply supported square tubes steel beams [J]. International Journal of Mechanical Science, 1985, 27(1/2): 55-69.

[3] Bambach M R. Behaviour and design of aluminium hollow sections subjected to transverse blast loads [J]. Thin-Walled Structures, 2008, 46: 1370-1381.

[4] Jama H H, Nurick G N, Bambach M R. Steel square hollow sections subjected to transverse blast loads [J]. Thin-Walled Structures, 2012, 53: 109-122.

[5] 孙韬，冯顺山.自由圆柱壳在侧向非对称脉冲载荷下的塑性破坏[J].爆炸与冲击，1998, 18(2): 103-111.

SUN Tao, FENG Shun-shan. Damage of free plastic cylinders under lateral impulsive loading [J]. Explosion and Shock Waves, 1998, 18(2):103-111.

[6] 路胜卓，张博一，王伟，等.爆炸作用下薄壁柱壳结构动力响应实验研究[J].南京理工大学学报：自然科学版，2011，35(5)：621-626.

LU Sheng-zhuo, ZHANG Bo-yi, WANG Wei, et al. Experimental research on dynamic response mechanism of thin cylindrical shell under blast loading [J]. Journal of Nanjing University of Science and Technology, 2011, 35(5):621-626.

[7] 刘理，刘土光，张涛，复杂载荷作用下圆柱壳的弹塑性动力屈曲研究[J].爆炸与冲击，2002，22(2)：119-125.

LIU Li, LIU Tu-guang, ZHANG Tao. Elastic-plastic dynamic buckling of cylindrical shells under combined loading [J]. Explosion and Shock Waves, 2002, 22(2):119-125.

[8] 纪冲，徐全军，万文乾，等.钢质圆柱壳在侧向爆炸荷载下的动力响应研究[J].爆炸与冲击，2014，34(2)：137-144.

JI Chong, XU Quan-jun, WAN Wen-qian, et al. Dynamic response of steel cylindrical shells under lateral explosion loading[J]. Explosion and Shock Waves, 2014, 34(2):137-144.

[9] 章冠人，陈大年.凝聚炸药起爆动力学[M].北京：国防工业出版社，1991.

[10] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperature[C]∥Proceedings of 7th Symposium on Ballistics. Hegue, Netherlands: International Ballistics Committee, 1983: 541-547.

[11] 宁建国，王成，马天宝.爆炸与冲击动力学[M].北京：国防工业出版社，2010：110-128.

Dynamic responses and damage modes of thin-walled square tubes subjected to explosion loading

SONG Ke-jian, LONG Yuan, JI Chong, GAO Fu-yin, LI xing-hua

(Engineering Institute of Engineering Corps, PLA University of Science and Technology, Nanjing 210007, China)

Abstract:Numerical simulations and experimental tests were carried out on the dynamic responses of thin-walled steel square hollow tubes subjected to explosion loading. The impact experiments of explosion loading caused by 200 g TNT charge on the steel square tubes were carried out. The deformation modes and damage modes were obtained under different conditions. The experimental results show that when the charge distance is greater than or equal to 14 cm, the structures will undergo local deformation only. When the charge distance is equal to 10 cm or 12 cm, the structures will undergo both local and global deformations. The experimental results also show that the two side walls facing explosion display long strip rupture damage. By using LS-DYNA, the deformation and damage processes of thin-walled tubes subjected to explosion loading were numerically simulated with Lagrangian-Eulerian coupling method. The deformation processes of thin-walled tubes as well as the deflection-time curves at some key points were also obtained. The dynamic responses of the square tubes affected by the width to thickness ratio were analysed. The results show that the deformation decreases with the decreasing of the width to thickness ratio.

Key words:thin-walled square tube; blast loading; dynamic response; damage mode

基金项目：国家自然科学基金(11102233)

收稿日期：2015-08-13修改稿收到日期：2015-10-17

通信作者纪冲 男，博士，副教授，1981年生

中图分类号:O383

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.021

第一作者 宋克健 男，博士生，1987年生