小型高光谱分辨率光栅单色仪的研制
杨增鹏,唐玉国,巴音贺希格,崔继承,杨 晋
1. 中国科学院长春光学精密机械与物理研究所,吉林 长春 130033 2. 中国科学院大学,北京 100049
小型高光谱分辨率光栅单色仪的研制
杨增鹏1, 2,唐玉国1,巴音贺希格1,崔继承1,杨 晋1
1. 中国科学院长春光学精密机械与物理研究所,吉林 长春 130033 2. 中国科学院大学,北京 100049
单色仪是成像光谱仪进行光谱连续定标的必备设备,为了对高光谱成像光谱仪进行连续光谱定标,设计了一种轻小型高光谱分辨率的光栅单色仪。采用水平式Czerny-Turner光路结构,以高光谱分辨率为出发点,通过推导计算,从光栅选型、焦距计算、狭缝尺寸的确定等方面详细论述了光栅单色仪的设计思路,给出仪器的重要必要结构参数,并论述了这些结构参数对仪器光谱分辨率和体积的影响。根据光栅单色仪的光路特点,对入射狭缝组件、准直物镜组件和成像物镜组件、扫描结构、机身等进行轻小型机械结构设计,并给出正弦杆扫描机构的结构参数与仪器输出波长和波长扫描精度的数学关系,完成了仪器的整体结构设计和装调。应用汞灯可见光光谱进行波长定标,采用最小二乘法得到定标曲线,并提出步进数极限误差与定标曲线相结合的方法,求得仪器的波长重复性和波长准确度;仪器在400~800 nm波长范围内,光谱分辨率优于0.1 nm,波长重复性达±0.096 6 nm,波长准确度达±0.096 9 nm。
光栅单色仪;高光谱分辨率;光学设计;正弦机构;波长定标
引 言
成像光谱仪是集精密光学和精密机械于一体的光学设备,是获取目标图像信息和光谱信息的必备设备,同时也是诸多领域进行科学研究的基础设备,如航空航天遥感、地质矿藏勘探、军事侦查、环境监测、医学研究等[1-5]。
成像光谱仪在使用之前,必须进行光谱定标。单色仪因能够提供连续、高稳定、高精度、高光谱分辨率的准单色光,成为成像光谱仪光谱定标的必备设备[6],所以非常有必要对单色仪进行研究。成像光谱仪进行光谱定标时,通常要求单色仪输出的准单色光光谱带宽小于成像光谱仪光谱带宽的1/10[7],即单色仪的光谱性能要高于成像光谱仪的光谱性能。目前,有关单色仪的文献[8-10]多数仅对仪器的某一指标进行讨论,未对影响仪器性能指标的各参数之间的关联性进行综合考虑。
为了对自主研发的棱镜-光栅成像光谱仪进行光谱定标,提出一种高性能、小型轻量化的光栅单色仪的详细设计思路,主要有三方面的研究:第一,以高光谱分辨率为出发点,通过理论计算,确定仪器的重要必要参数并完成仪器的光学设计;第二,从工程实现角度考虑,通过优化扫描结构及倾斜放置扫描机构,并采用分层设计的方法,在保证高光谱分辨率的同时,实现单色仪的小型化设计;第三,完成光栅单色仪的装调和光谱定标工作,使仪器达到技术指标。
1 光学设计
1.1 工作原理及主要技术指标
高光谱分辨率单色仪的整体结构如图1所示。复色光信号通过光纤跳线传入到仪器入射狭缝S1处形成点发散光束,发散光束经装有滤光片的光阑滤光,再由平面反射镜1折转光路后照射到球面准直物镜M1上,平面光栅G对经准直物镜M1反射后的平行光束进行色散分光,色散后的平行光束照射到球面成像物镜M2上会聚,会聚光束经平面反射镜2折转光路后成像于出射狭缝S2处,通过扫描机构转动光栅实现在出射狭缝S2处输出不同波长的光,探测器将准单色光转换为数字信号并将数据发送至计算机,从而得到相应光谱信息。
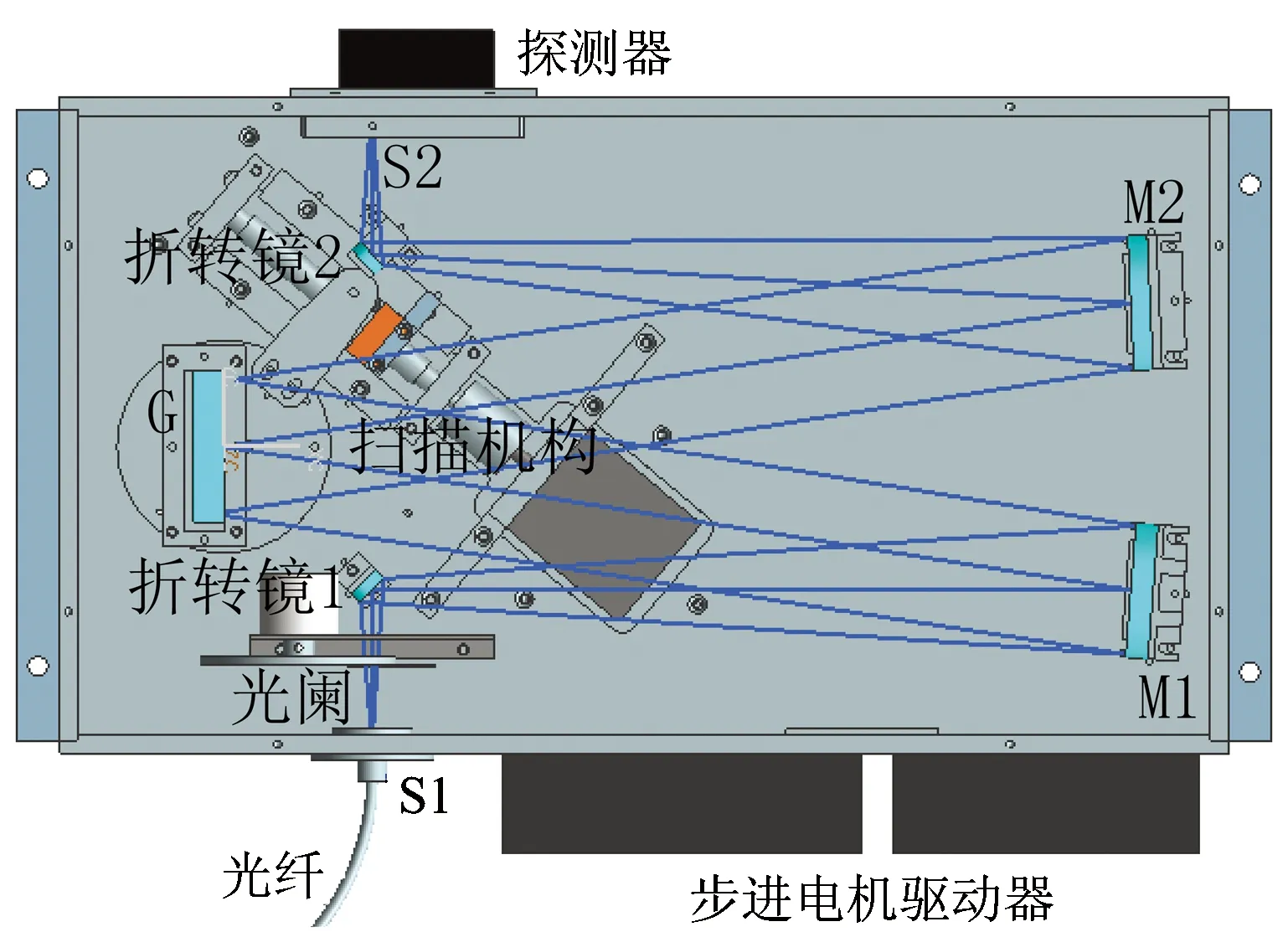
Fig.1 Schematic diagram of the monochromator
根据成像光谱仪光谱定标工作的实际需求,对自主研发的高光谱分辨率光栅单色仪提出了如表1所列的主要技术指标。

Table 1 Parameters of the system
1.2 系统主要结构参数计算
1.2.1 光栅刻线密度计算
目前,在所要求的波段范围内平面光栅具有较高的衍射效率,为了保证光栅单色仪的能量传输效率,选择平面光栅作为核心色散元件。图2所示为光栅的微观截面结构。
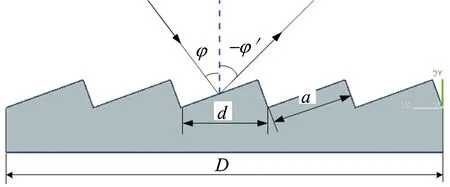
Fig.2 Structure of the grating
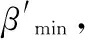
(1)
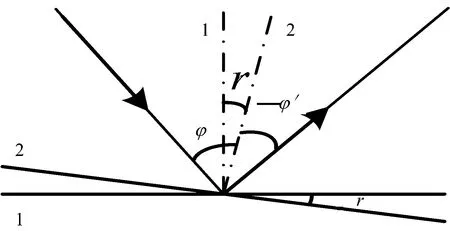
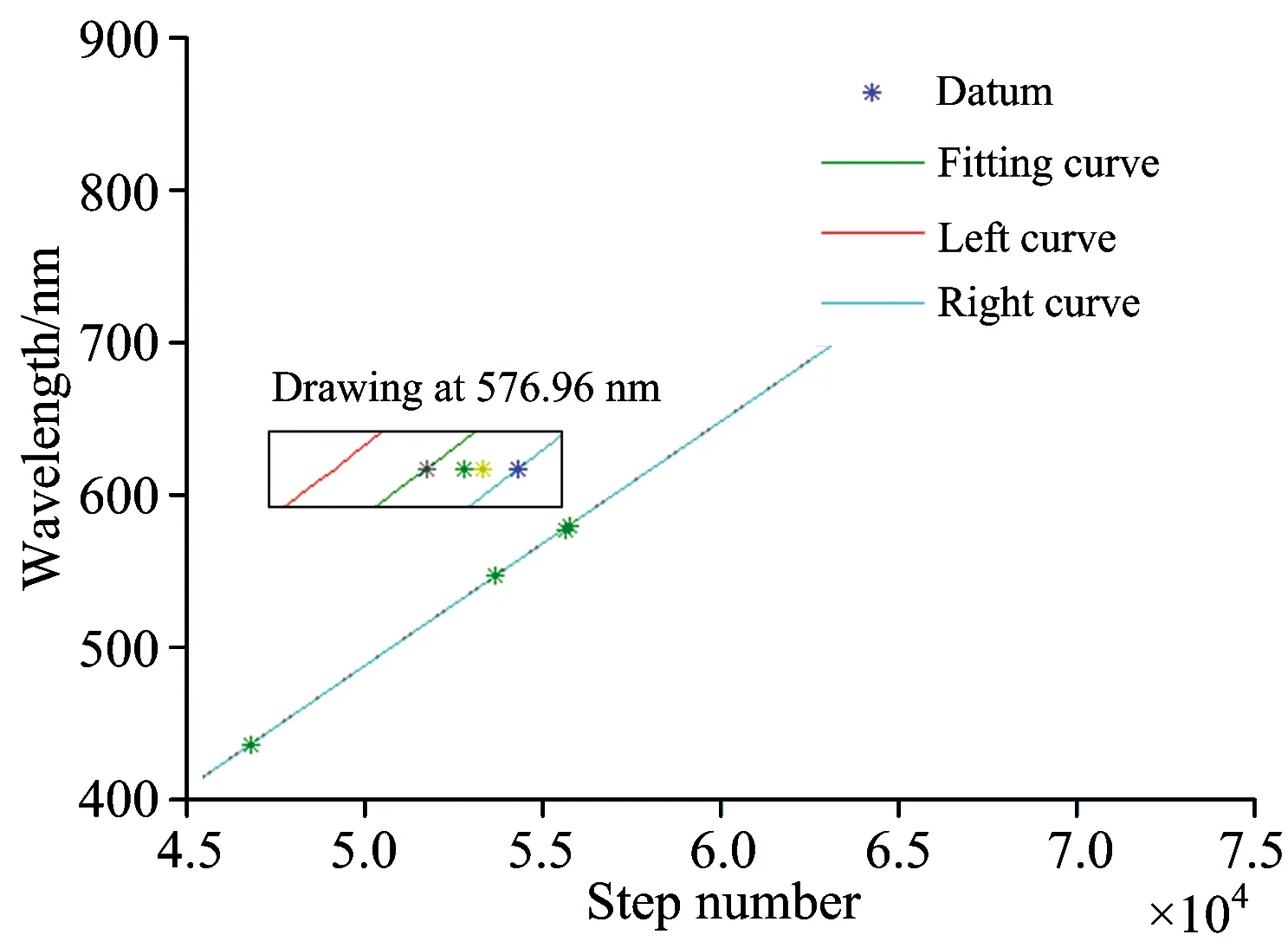
式中,λ为波长,a为刻痕工作面宽度。由此可知,对于确定波长而言,只有减小a才能使得光能量分布于较宽的波长范围内,但要求λ (2) 式中,ν为光栅刻线密度。当λmax=800 nm时,νmax=1 250 l·mm-1。 (3) 1.2.2 光栅闪耀波长计算 一般认为,相对衍射效率大于0.4的波长范围即可满足使用要求,对于将要选择的闪耀光栅,这个波长范围可由以下的经验公式[10,12]得到 (4) 式中,λb为第一级次的闪耀波长。查询光栅产品规格表,选择第一级次光谱闪耀的光栅,m=-1,λb=540 nm,则有用的波长范围为:360 nm<λ<1 080 nm,覆盖仪器工作波段。 1.2.3 自由光谱区计算 自由光谱区σλ即为光谱不重叠区,由以下公式[11]决定 (5) 式中,λmax为自由光谱区最大波长,λmin为自由光谱区最小波长,求得 (6) 因光源信号通常包含小于工作波段的短波(小于400 nm的光波),为保证输出波长的纯度,要求光栅单色仪在工作波段内输出波长无谱线重叠情况,因此在入射狭缝后安装阻带限为400 nm的高通滤光片消除短波高级次谱线。 1.2.4 物镜焦距计算 1.2.5 光栅尺寸计算 光栅所能分辨的最小波长差Δλ,由以下公式[13]决定 (7) 1.2.6 狭缝宽度计算 对于光栅单色仪,影响其输出光谱带宽的因素很多,如狭缝宽度、系统像差及离焦量等,而系统像差可由光学设计优化减小,离焦量可通过装调减小。由入射狭缝和出射狭缝共同作用分离出来的光束带宽δλ[12]为 (8) 式中,δ1λ为入射狭缝分离的光谱带宽,δ2λ为出射狭缝分离的光谱带宽,a1为入射狭缝宽度,a2为出射狭缝宽度,γ为光栅在子午面内的角放大率。由此可知,狭缝宽度越窄,获得的光谱纯度越高。令入射狭缝和出射狭缝等宽,取γ=1,δλ=0.1nm,计算得:a=20μm。简化计算时,γ被放大,故可取a=20μm。 1.2.7 光栅转角公式推导 在单色仪中,光栅栅面入射光线和输出衍射光线的夹角为固定值,令其等于2θ,如图3所示。通过转动光栅,使得不同波长的准单色光在出射狭缝处输出。 Fig.3 Principle diagram of the grating diffraction 假设1位置为光栅初始位置(零级谱位置),则入射角等于出射角。当光栅转动角度r到达位置2时,则 (9) 将式(9)代入光栅方程并进行三角变换,推得光栅相对于初始位置转动的角度与相应输出波长的关系式为 (10) 综上所述,经过计算,单色仪的必要参数如下: 工作波段:400~800 nm;光谱分辨本领:0.1 nm;光栅参数:1 200 l·mm-1,λb=540 nm,50 mm×50 mm×10 mm;准直物镜焦距:300 mm;成像物镜焦距:300 mm;入射狭缝宽度:20 μm;出射狭缝宽度:20 μm。 1.3 光学仿真设计 采用光学软件对单色仪进行仿真设计,单色仪采用对称式Czerny-Turner光路结构,选择边缘波长及中心波长800,600和400 nm为参考波长,入射狭缝物面选择(0, 0),(1.5 mm, 10 μm),(1.5 mm, -10 μm),(-1.5 mm, 10 μm)和(-1.5 mm, -10 μm)五个点为参考点,对光学系统在出射狭缝处的成像情况进行考察;通过光线追迹,调整光路结构,对系统像差进行校正,使之满足技术指标,光学结构如图4所示。初始光路在长度方向较长,宽度方向上仅为136 mm,考虑到准直物镜支架、成像物镜支架、光栅转台等组件的体积,在光路结构中加入两片用于光路转折的平面反射镜来放大仪器宽度从而减小长度,同时此光路结构也可有效减少仪器杂散光。 Fig.4 Simulation of the optical system 光栅单色仪仅对光谱分辨率有要求,而弧矢方向的像差对光栅单色仪的光谱分辨率并无影响,所以仅对系统的子午像差进行严格校正。光栅栅面处的出射光束与入射光束之间的夹角为2θ=18°。系统点列图如图5所示,在400~800 nm波段范围内,出射光谱均能以0.1 nm分开。通过光线追迹,得到入射狭缝在出射狭缝处的像的尺寸如表2所示。 Fig.5 Spot diagram of the optical system Table 2 Results of the real ray trace 根据光学设计结果,结合式(10),可得光栅单色仪输出400 nm波长时,从零级谱位置光栅需转动角度r400=14.063 2°,同理,r800=29.076 9°。当光栅单色仪输出波长从400 nm扫描到800 nm时,光栅所需转动的角度为r总=15.013 7°,光学软件模拟验证,光栅转动相应角度时,出射狭缝处输出了相应波长的光谱。 光栅单色仪机械结构的设计是利用具体零件的结构组合,使仪器经济合理地实现总体设计提出的原理方案和操作要求,同时保证仪器的光学性能。光栅单色仪机械结构设计时,以机身组件中的底面作为定位参考面,保证各光学元件的中心高度相等及各光学元件的空间定位准确,通过合理的空间布局及各组件的小型化设计来实现仪器整体小型化。 2.1 入射狭缝组件设计 入射狭缝组件由玻璃狭缝和支架组成。为保证入射狭缝均匀、无毛刺、无缺口,狭缝采用光刻铬板制作,狭缝宽a=20 μm,高b=5 mm。光信号采用光纤跳线导入单色仪,有利于仪器的小型化设计。光纤芯径为1 000 μm,数值孔径NA=0.37,大于仪器的数值孔径,则在入射狭缝后加入限制光束孔径的光阑以减少仪器内部杂散光。 2.2 准直物镜组件设计 准直物镜组件由球面反射镜和支架组成。为减少结构复杂度及利于小型化设计,采用胶结剂将反射镜粘结于支架上。球面反射镜由K9玻璃制作,径向最大尺寸与反射镜最小厚度之比应小于6∶1,以便固化或者极端温度条件下,胶结层体缩不会造成光学表面变形。为了获得最大的胶结强度,胶结层厚度和面积应当受到控制,薄的胶结层要比厚的更为牢固,而最小粘结面积Smin,由以下公式[14]决定 Smin=WaGgfs/J (11) 式中,W为光学零件的重量,aG为最恶劣条件下的加速度系数,g为重力加速度,fs为安全系数,J为粘结区的抗剪强度或抗拉强度。取W=0.028 4 kg,aG=500,fs=10,J=22 MPa,计算得:Smin=64.5 mm3。 2.3 扫描机构设计 光栅单色仪通过转动光栅实现不同波长的输出,光栅转角精度直接影响仪器输出波长的精度,因此,转动机构的设计至关重要。正弦杆扫描机构具有结构简单,扫描精度易提高,重复性好,易于制作和装调等优点,所以采用正弦杆扫描机构作为光栅转动机构,如图6所示。为提高扫描精度,杠杆与丝母的接触面、丝母与导向槽的接触面均采用高运动副,即丝母工作面均为平面,杠杆工作面为一滚动圆柱面,导槽工作面为直线[15]。光栅转台与基座采用轴承连接,光栅工作转速较慢,则转台与轴承采用较为严格的间隙配合,通过隔圈及挡板给予轴向预紧力来固定轴承。光栅刻线与基底侧面垂直度可能存在偏差,所以光栅基座的设计应考虑俯仰调节和滚转调节。 Fig.6 Schematic diagram of the sine mechanism 根据式(10)和图6,输出波长与转角之间的关系式为 (12) 式中,κ=2dcosθ,计算得:κ=1 646.15 nm。对式(12)微分可得 (13) 丝杆采用步进电机转动,步进电机最小步距角为1.8°,丝杆螺纹导程为0.5 mm,步进电机细分数为nx=4,步进电机每走一步dh为 (14) (15) 取K=25nm·mm-1,重新计算l得:l=65.85nm。K的意义表明,丝母每平移1mm,出射狭缝处光谱扫描了25nm。扫描机构整体布局时,丝杆、连轴节及步进电机长度之和大于仪器宽度,在保证光栅单色仪光学性能的前提下,将扫描机构倾斜置于箱体内,实现了仪器的小型化设计。 2.4 机身组件设计 仪器机身设计时,采用双层结构设计以使仪器小型化。在保证长宽不变的情况下,向高度方向拓展机械布局,上层为分光系统,下层进行电子元器件排布,主要包括电源和控制器系统。图7所示为单色仪实体结构,整体体积为383×248×129mm3。 Fig.7 Photo of the monochromator 为保证光栅零位置时杠杆与丝杆的垂直度,装调时选择螺孔边缘为参考面进行安装,则l=63.85 mm。步进电机细分数nx=4,由式(12)和式(13)联合解得步进电机单步扫描波长为0.016 1 nm。 采用汞灯可见光谱区的一级谱及435.83 nm的二级谱进行波长定标,进行多次重复实验,得到汞灯各谱线的强度峰值处的电机步进数平均值如表3所列。 步进数与波长的数学关系采用最小二乘法进行拟合,可得到线性、二次、三次、四次拟合多项式,经计算验证,三次拟合多项式求解的拟合波长偏差最小,如表4所列,最大波长偏差仅为0.031 9 nm,因此,选择三次拟合多项式为步进数与波长的定标函数,如式(16)所示。 λ=2.170 4×10-13n3-3.887 09×10-8n2+ 0.018 318 6n-359.927 (16) 对定标函数(16)求导 dλ=(6.511 2×10-13n2-7.774 18×10-8n+ 0.018 318 6)dn (17) 当dn=1,n取表3所列步进数时,解得步进电机单步所扫描的波长分别为:0.016 1,0.016,0.016,0.016和0.016 1 nm,与理论值相符。整个工作波段范围内,步进电机扫描0.1 nm时,扫描所需最小步进数约为6.2步。 Table 3 The step number of stepper motor at different wavelengths Table 4 Wavelength indication error(unit:nm) 对各波长处的电机步进数数据组进行数据处理,求得每一标准谱处的步进数的标准差为:0.98,1.87,1.94,1.83和0.98,置信系数t=3时,则步进数最大极限误差为δmax=5.82。将定标函数和多组步进数-波长的实验数据绘于图8中,令定标函数曲线沿n轴分别左右平移±6步得到两条曲线,可以看到所有数据点均落于两条曲线间,而两条曲线的横向平移步进数±6即为仪器的波长重复精度,为±0.096 6 nm;纵向最大波长差即为波长准确度,为±0.096 9 nm。 Fig.8 Schematic of the fitting curve for wavelength 光谱分辨率δλ通常表示为各波长光谱响应函数的全波半高宽。如图9所示,为546.07 nm处的扫描高斯拟合光谱响应函数,光谱分辨率为0.096 6 nm(6步)。 Fig.9 Define illustration of wavelength resolution 通过对实验数据的测量和分析,证明此单色仪在400~800 nm波段范围内,波长重复性达±0.096 6 nm,波长准确度达±0.096 9 nm,光谱分辨率优于0.1 nm。 根据使用要求,提出一种光栅单色仪的详细设计方法,实现了小型高光谱分辨率光栅单色仪的光机设计。对光栅单色仪的光谱定标数据进行分析处理,确定单色仪在400~800 nm波段范围内波长重复性达±0.096 6 nm,波长准确度达±0.096 9 nm,光谱分辨率达0.1 nm。这种设计方法的意义在于:(1)从实际需求出发,以高光谱分辨率为出发点,对光栅单色仪的基本参数进行理论计算,为光栅单色仪的设计提供理论依据;(2)从工程角度考虑,通过加入折转镜,采用双层结构,对单色仪内部空间进行合理布局,在保证单色仪高光谱分辨率的同时,实现了仪器的小型化;(3)通过对光栅单色仪进行光谱定标及数据分析,确定仪器达到所要求的技术指标,证明了该设计方法可靠,也可为其他光栅光谱仪的研制提供了参考和借鉴。 [1] Robert O Green, Michael L Eastwood, Charles M Sarture, et al. Remote Sensing of Environment, 1998, 65(3): 227. [2] LIU Yu-juan, CUI Ji-cheng, Bayanheshig, et al(刘玉娟, 崔继承, 巴音贺希格, 等). Optics and Precision Engineering(光学 精密工程), 2012, 20(1): 52. [3] TANG Yi, ZHANG Zhi-ge, CHEN Ting-ai, et al(唐 义, 张止戈, 陈廷爱, 等). Acta Optica Sinica(光学学报), 2013, 33(3): 0330004. [4] CUI Ji-cheng, TANG Yu-guo, HAN Peng-peng, et al(崔继承, 唐玉国, 撖芃芃, 等). Optics and Precision Engineering(光学 精密工程), 2013, 21(12): 3043. [5] YANG Zeng-peng, TANG Yu-guo, Bayanheshig, et al(杨增鹏, 唐玉国, 巴音贺希格, 等). Acta Optica Sinica(光学学报), 2014, 34(9): 0911003. [6] QI Xiang-dong, HAN Peng-peng, PAN Ming-zhong, et al(齐向东, 撖芃芃, 潘明忠, 等). Optics and Precision Engineering(光学 精密工程), 2011, 19(12): 2870. [7] JIN Hui, JIANG Hui-lin, ZHENG Yu-quan, et al(金 辉, 姜会林, 郑玉权, 等). Chinese Journal of Luminescence(发光学报), 2013, 34(2): 235. [8] LIU Han-chen, WANG Qiu-ping, ZHANG Chong-hui, et al(刘汉臣, 王秋萍, 张崇辉, 等). Journal of Applied Optics(应用光学), 2008, 29(4): 595. [9] WANG Xing-quan, FENG Ke-cheng, ZHU Guo-xian, et al(王兴权, 冯克成, 朱国贤, 等). Acta Photonica Sinica(光子学报), 2009, 38(5): 1167. [10] CHEN Shao-jie, TANG Yu-guo, Bayanheshig, et al(陈少杰, 唐玉国, 巴音贺希格, 等). Chinese Journal of Optics and Applied Optics(中国光学与应用光学), 2009, 2(4): 322. [11] WU Guo-an(吴国安). Spectral Instrument Design(光谱仪器设计). Beijing: Science Press(北京: 科学出版社), 1978. 108, 3, 103. [12] LI Quan-chen, JIANG Yue-juan(李全臣, 蒋月娟). Principle of Spectrograph(光谱仪器原理). Beijing: Beijing Institute of Technology Press(北京: 北京理工大学出版社), 1999. 60, 201. [13] SHI Shun-xiang, WANG Xue-en, LIU Jin-song(石顺祥, 王学恩, 刘劲松). Physical Optics and Applied Optics(物理光学与应用光学). Xi’an: Xidian University Publisher(西安: 西安电子科技大学出版社), 2008. 168. [14] Paul R,Yoder Jr. Opto-Mechanical Systems Design(光机系统设计). Translated by ZHOU Hai-xian, CHENG Yun-fang(周海宪,程云芳,译). Beijing: China Machine Press(北京:机械工业出版社), 2008. 397. [15] QIU Zu-rong(裘祖荣). Fundamentals of Precise Instrument Design(精密机械设计基础). Beijing: China Machine Press(北京:机械工业出版社), 2007. 95. Research on Small-Type and High-Spectral-Resolution Grating Monochromator YANG Zeng-peng1, 2, TANG Yu-guo1, Bayanheshig1, CUI Ji-cheng1, YANG Jin1 1. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China 2. University of Chinese Academy of Sciences, Beijing 100049, China Monochromator is the necessary equipment for spectral imager to calibrate the spectrum continuously. In order to calibrate the hyperspectral imaging spectrometer continuously, a small-type and high-spectral-resolution grating monochromator is designed. The grating monochromator with horizontal Czerny-Turner structure is designed with high-spectral-resolution as a starting point, and the design idea is discussed in detail from choosing the grating, calculating the focal length, the sizes of entrance slit and exit slit, among others. Using this method, the necessary structure parameters are determined, and the impact of the necessary structure parameters for spectral resolution and volume is given. According to the optical characteristics of the grating monochromator, the mechanical structures of the instrument are designed for small and handy from the components of the entrance slit, the collimator lens and imaging objective lens, the scanning structures, the fuselage and so on. The relationship of the sine mechanism parameters for output wavelength and wavelength scanning accuracy is given. The design and adjustment of the instrument are completed. The visible spectrums of mercury lamp are used as calibration lines, and the calibration curve is acquired by using least square method. This paper gives a method that combining the limit error of the step number and the calibration curve to evaluate the wavelength repeatability and wavelength precision. The datum of experiment shows that the spectral resolution of the instrument is better than 0.1 nm in the wavelength band from 400 to 800 nm. Simultaneously the wavelength repeatability reach to ±0.096 6 nm and the precision reach to ±0.096 9 nm. Grating monochromator; Hyperspectral; Optical design; Sine mechanism; Wavelength calibration Jul. 25, 2014; accepted Dec. 6, 2014) 2014-07-25, 2014-12-06 国家自然科学基金项目(61108032),江苏省自然科学基金项目(BK2012188),国家重大科学仪器设备开发专项(2011YQ120023)和吉林省科技发展计划项目(20126012)资助 杨增鹏,1987年生,中国科学院长春光学精密机械与物理研究所博士研究生 e-mail:175367864@qq.com TH744.1 A 10.3964/j.issn.1000-0593(2016)01-0273-06

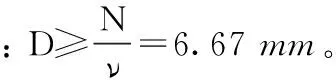




2 机械设计



3 实验及波长定标



4 结 论

