某型轮式装甲车辆局部路径规划研究
——一种考虑人类视觉特点的几何算法
薛 青,孙松涛,2,陈 琳,丁 苹,2
(1.装甲兵工程学院,北京 100072; 2.总参陆航部,北京 101114)
某型轮式装甲车辆局部路径规划研究
——一种考虑人类视觉特点的几何算法
薛青1,孙松涛1,2,陈琳1,丁苹1,2
(1.装甲兵工程学院,北京100072; 2.总参陆航部,北京101114)
摘要:为了提高轮式装甲车辆局部路径规划能力,满足装备作战仿真的需求,在基本几何算法的基础上考虑人类视觉特点,提出了一种基于坐标变换的几何算法用于轮式装甲车辆局部路径规划。经过仿真实验与对比分析,该算法在运算速度上有明显优势,既能满足实时性要求,也能真实反映作战人员野战机动特点,是一种实用的局部路径规划方法。
关键词:路径规划;改进几何算法;装甲车辆;视觉
轮式装甲车辆局部路径规划是指在全局规划的路径机动过程中,遇到新的障碍物后迅速做出反应,待完成局部避障处理后,再回到预先规划的全局路径上机动[1]。因此,局部路径规划算法要求实时性强,计算效率高。目前,常用的局部路径规划算法有A*算法、人工势场法、遗传算法等[2-5],但存在一些不足之处,例如A*算法对启发函数依赖程度高;人工势场法容易在障碍物前振荡;遗传算法搜索时间长、局部寻优能力不足等[6-8]。本研究根据几何理论,同时考虑人类视觉特点,研究一种几何算法用于轮式装甲车辆局部路径规划,仿真结果表明,该算法简便高效,能够满足路径规划实时要求。
1算法原理
研究表明,视觉是人类感知信息的主要来源,人类80%以上的信息都是由视觉提供的。但是,视觉也有局限性:单眼视野约150°,双眼视野约180°,中间120°为双眼共有的有效视觉范围;在垂直方向上的视野为视平线上50°和视平线下70°范围。因此,本研究设计一种符合人类视觉特点的几何算法,着重考虑轮式装甲车辆眼前的局部环境信息,而不考虑后面的障碍物情况,这样得到的可能不是最优路径,但却符合作战人员的局部路径规划特点。
在野战环境下,轮式装甲车辆按照预先规划的全局路径机动时,一般会遇到一些新的局部障碍物,例如弹坑、断桥等,当这些障碍物进入轮式装甲车辆的探测范围时,首先会判断当前障碍物是否在前进方向上。如果在当前行进方向上,则要基于两点之间直线距离最短的原则,分析怎样绕过这个障碍物,即根据具体环境的经验判断,选择一个可行驶路径点避开当前这个障碍物。在这些情况下,大多数作战人员会凭视觉感知规划行驶路径,得到的规划路径不一定是最优的,但是大致方向没有变,对全局路径规划影响不大。
算法的整体思路:在初始坐标系中,以轮式装甲车辆发现障碍物时的位置为相对原点o′,以目标方向为o′x′建立相对直角坐标系x′o′y′,于是o′x′可以将障碍物分为上、下两个集合,然后选择轮式装甲车辆当前位置o′所能观察到的障碍物可通过边缘顶点作为备选路径点,计算出上、下两个方向集中备选路径点的行驶方向角,找出上、下两个方向集中行驶方向角最大的两个点,通过对比选择这两点中行驶方向角小的那一个作为“最佳路径点”。
2坐标空间描述
采用可视图法建立虚拟三维空间模型,障碍物则采用欧氏平面里的凸多边形表示,而对于存有凹点的多边形,可以通过求取凸壳得到包含这些凹顶点的最小凸多边形。为便于描述先确定几个定义:
定义1:设障碍物o为有限平面区域,该区域由一系列点P1,P2,…,PN首尾相连所围成,Pi(i=1,2,…,N)是多边形o的顶点,相邻顶点的连线PiPi+1是多边形o的边界。若多边形o的所有顶点都位于连线PiPi+1的一侧(除去直线上的两点),则称该多边形o为凸多边形。
定义2:设机动中的轮式装甲车辆当前位置为r,接连的下一个可选路径点为T,其中T是从凸多边形的顶点产生的,连线rt的方向称为轮式装甲车辆的行进方向。
定义3:设机动中的轮式装甲车辆当前位置为r,接连的下一个子目标点为G,其中G是预先全局路径规划中r接连的下一个路径点,连线rg的方向称为轮式装甲车辆目标方向。
定义4:机动中的轮式装甲车辆目标方向与行进方向之间的夹角称为路径方向角δ。
本研究采用虚拟三维环境中的大地平面坐标和轮式装甲车辆两种坐标空间。如图1所示,其中大地平面坐标系xoy为绝对坐标系,也称全局坐标系,用于表示起始点位置、目标点位置以及轮式装甲车辆每一时刻的位置,以便于在轮式装甲车辆每一次局部路径规划都能直接转化为全局坐标。x′o′y′为相对坐标系,代表轮式装甲车辆的局部坐标空间,用于计算路径方向角,以轮式装甲车辆的当前位置为相对原点o′,横轴o′x′方向则表示目标方向。两种坐标系的坐标变换按如下方法计算:
设o′点在xoy坐标系中的坐标值为(A,B),ox与o′x′的夹角为θ,若已知顶点A在xoy坐标系中的坐标为(x,y),可按式(1)转换为x′o′y′坐标系中的坐标(x′,y′)

(1)
同理,可实现相对坐标系到绝对坐标系的变换,若已知顶点A在x′o′y′坐标系中的坐标为(x′,y′),可按式(2)将其转换为xoy坐标系中的坐标(x,y)
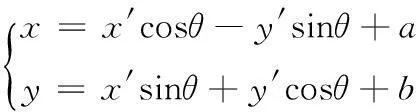
(2)
其中:式(1)称为正变换,式(2)称为逆变换。通过以上的坐标空间描述,可将障碍物o映射到坐标系x′o′y′中。

图1 坐标空间示意图
3算法设计
轮式装甲车辆在预先规划的全局路径上行驶时,目标方向左右共计120°范围内发现障碍物后可按照以下操作流程进行局部路径规划,其算法流程如图2所示。
步骤1:首先进行坐标正变换。为便于判断,可采用相对坐标系x′o′y′来计算,如图3所示,多边形o1表示局部出现的障碍物,在绝对坐标系xoy中,以轮式装甲车辆的当前位置r为原点,以rg为横轴建立相对坐标系x′oy′,由初始条件可知多边形o1各顶点在绝对坐标系xoy下的坐标,由式(1)分别求得可看到的各顶点在相对坐标系x′oy′下的坐标。
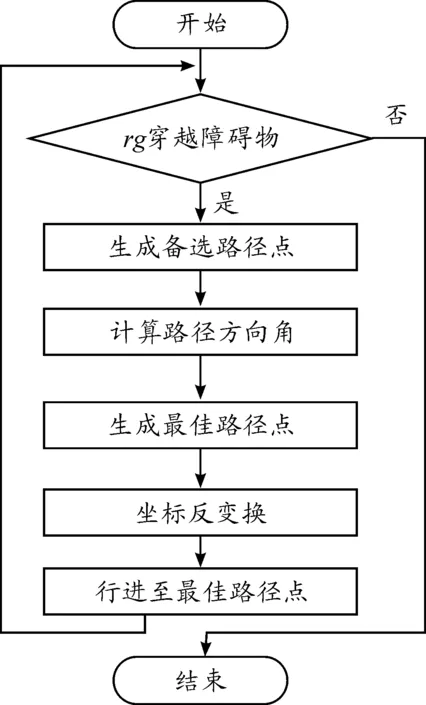
图2 算法流程
步骤2:判断目标方向rg是否穿越障碍物。逐个比较可看到的各顶点在相对坐标系x′o′y′下的纵坐标值:若都大于0或都小于0,则目标方向rg不会与该障碍物相交,转至Step6;若存在同时大于0和小于0的情况,则目标方向rg会与该障碍物相交,将障碍物顶点分为上、下两个集合,假设相交情况如图3所示。
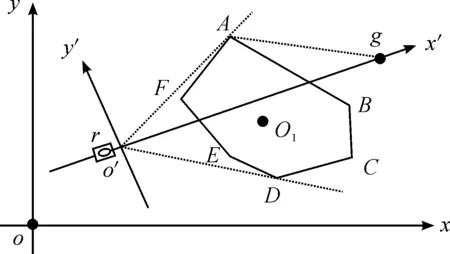
图3 算法示意图
步骤3:分别计算路径方向角。考虑到人类视觉局限性,轮式装甲车辆位于当前位置r时,作战人员只能把看到A、d、E、f4个障碍物顶点作为备选路径点,根据各个顶点在相对坐标系x′o′y′下的坐标,分别计算路径方向角δ,以A点为例,其路径方向角计算公式如下
(3)
步骤4:选择“最佳路径点”。分别比较上顶点集合和下顶点集合中各个路径方向角的大小,选取上、下各一个最大路径方向角作为备选路径,然后在上、下两个备选路径中选取路径方向角较小的一个作为“最佳路径点”。假设上顶点集中的备选路径点表示为{(xi′,yi′)∪yi′>0},下顶点集中的备选路径点表示为{(xj′,yj′)∪yj′<0},最佳路径方向角记作δbest,则有式(4):
(4)
步骤5:进行坐标反变换。按照式(2)计算“最佳路径点”在xoy坐标系下的坐标,待轮式装甲车辆行进至该点后,接着将该点确定为新的当前位置,返回步骤1进行新一轮局部路径规划。
步骤6:若未发现目标方向上有相交的障碍物,轮式装甲车辆可直接行进至子目标点G。
4实验对比分析
将仿真实验与传统的A*算法和遗传算法的仿真结果进行对比分析。实验参数设置如下:A*算法的启发函数H(N)定义为轮式装甲车辆从当前位置到目标位置的估计路径长度;遗传算法的种群大小为150,交叉概率、变异概率分别取0.8、0.1,终止进化代数为200。计算机基本配置为Pentium(R)D CPU 3.0 GHz,内存2 GB,在Windows XP系统下用Visual C++ 6.0和Matlab R2007进行仿真程序设计开发。实验时选择3种算法的路径长度和运行时间这两个指标进行对比分析,为消除实验中的误差,每种算法各进行10次实验,并对实验结果进行平均处理。实验结果如表1、表2所示。

表1 路径长度比较 m

表2 运算时间比较 s
通过对表1和表2的实验结果进行分析可以得出如下结论:
1)路径长度方面:遗传算法所规划的路径长度最短,A*算法和几何算法所规划的路径长度差别不大。主要是因为由于遗传算法是经过迭代计算,可以找到最优最短路径;A*算法对启发函数的依赖性较强,难以保证每次搜索到的都是最短路径,有可能是次短路径;几何算法是根据当前位置和目标位置以及障碍物备选路径点的连线计算路径方向角,通过对比分析,选择相对小的路径方向角,仅考虑当前所看到的障碍物,不了解障碍物后面的情况,所选路径不一定最短。
2)运算时间方面:几何算法的运算时间最少,A*算法和遗传算法都明显多于几何算法。这是因为几何算法考虑人类视觉局限性,仅判断当前位置到目标点连线上的障碍物,也仅选择当前位置所能够观察到的障碍物顶点作为备选路径点用以计算备选路径角,同时计算方法也比较简单,算法运行效率较高;A*算法在进行路径规划时对启发函数依赖较大,需要计算启发函数用以评估待扩展的节点值,并且可能经常要扩展到整个全局路径规划空间才能搜索到理想路径,所需时间明显多于几何算法;而遗传算法在进行路径规划时需要进行循环迭代计算,并且都需要通过选择、交叉、变异、删除、插入等遗传算法操作,运算时间最长。图4是表1和表2中实验结果的直观显示。
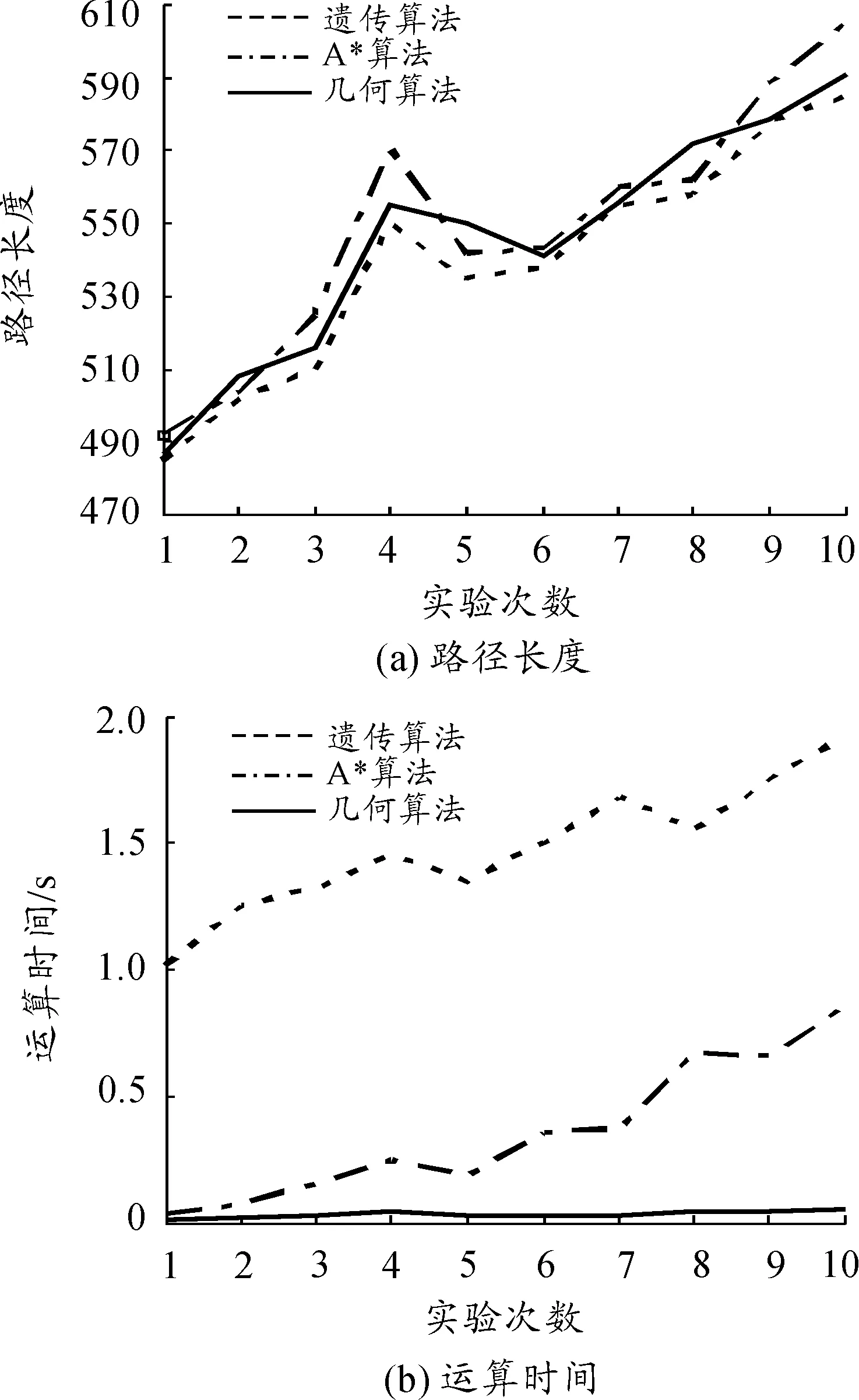
图4 3种算法实验对比曲线
综上所述,考虑人类视觉特点的几何算法在运算时间方面的优势明显,所得到的路径却不是最短路径。但是作战环境下的局部路径规划应首先考虑实时快速性要求,继而兼顾局部路径规划长度,这样才能够满足战场环境瞬息万变的要求。由于几何算法运算速度快,算法相对简单,因此,采用几何算法进行局部路径规划的轮式装甲车辆在发现新出现的障碍物后能够迅速做出规避动作,按新规划路径继续机动,这满足实战化训练要求,能够真实反映作战人员野战机动特点,是一种实用的局部路径规划方法。
5结论
本文对轮式装甲车辆局部路径规划方法进行了深入研究,分析了传统的局部路径规划方法的优劣,结合人类视觉特点提出了一种基于坐标变换的几何算法方法用于装备作战仿真研究,结果表明该方法有效提高了轮式装甲车辆局部路径规划能力,运算速度明显提高,所选路径虽然不一定是最短或次短路径,但符合作战人员的局部路径规划特点,满足野战环境下的实时性需求,是一种实用的轮式装甲车辆局部路径规划方法。
参考文献:
[1]薛青.装备作战仿真基础[M].北京:国防工业出版社,2010.
[2]赵志辉,朱亚红,刘素兵,等.定积分的几何算法[J].高等数学研究,2014,17(6):38-40.
[3]陈小燕,张圣贵.一类凸规划问题的几何算法[J].福建师范大学学报,2012,28(2):7-10.
[4]闫守住,薛青,罗佳,等.基于免疫遗传算法的轮式装甲车辆CGF路径规划研究[J].四川兵工学报,2014(10):25-28.
[5]张海英,范进桢.移动机器人路径规划研究现状及展望[J].微型机与应用,2011,30(2):5-8.
[6]栗红生,刘莹.复杂路径下机器人路径规划优化方法仿真[J].计算机仿真,2012,31(1):407-411.
[7]杨柳,张洪,高忠国.基于人工势场法的移动机器人路径规划研究[J].机床与液压,2011,39(9):68-70.
[8]赵开新,王东署.未知环境中自主机器人的路径规划研究[J].郑州大学学报,2011,34(5):74-79.
(责任编辑周江川)
本文引用格式:薛青,孙松涛,陈琳,等.某型轮式装甲车辆局部路径规划研究——一种考虑人类视觉特点的几何算法[J].兵器装备工程学报,2016(5):25-28.
Citation format:XUE Qing,SUN Song-tao,CHEN Lin,et al.Research of One Wheeled Armored Vehicle Local Path Planning: A Geometric Algorithm Considering the Characteristics of Human Vision[J].Journal of Ordnance Equipment Engineering,2016(5):25-28.
Research of One Wheeled Armored Vehicle Local Path Planning: A Geometric Algorithm Considering the Characteristics of Human Vision
XUE Qing1,SUN Song-tao1,2,CHEN Lin1,DING Ping1,2
(1.Academy of Armored Force Engineering,Beijing 100072,China;2.Army Aviation Department,Beijing 101114,China)
Abstract:In order to improve the ability of the wheeled armored vehicle local path planning and to satisfy the needs of equipment fight simulation,this paper proposed a geometric algorithm for local path planning of wheeled armored vehicle based on the basic geometric algorithm.Through simulation experiments and contrastive analysis,this algorithm is a practical method of local path planning,and it perform superiority obviously at running speed,and it meets the real-time requirements,and it reacts the characteristics of the warfighter field motor truly.
Key words:path planning;improved geometric algorithm;armored vehicle;vision
doi:【装备理论与装备技术】10.11809/scbgxb2016.05.007
收稿日期:2015-11-28;修回日期:2015-12-30
作者简介:薛青(1961—),男,教授,博士生导师,中国计算机用户协会仿真应用分会副理事长,主要从事装备作战与保障仿真研究。
中图分类号:TJ811;TP391
文献标识码:A
文章编号:2096-2304(2016)05-0025-04

