圆柱状卫星侧表面温度场均匀化设计
程雪涛,徐向华,梁新刚
(清华大学 航天航空学院,北京 100084)
圆柱状卫星侧表面温度场均匀化设计
程雪涛,徐向华,梁新刚
(清华大学 航天航空学院,北京100084)
摘要:温度场均匀化设计因有利于航天器的稳定高效运行而获得越来越多的重视。本文针对简化的圆柱状卫星,采用仿生优化方法对给定量的高导热材料进行优化分布,以均匀化卫星侧表面温度场。同时,本文还基于理论分析了温度场均匀化过程中卫星的导热热阻和辐射热阻的变化情况,讨论了太阳光入射角度对卫星侧表面温度场的影响。结果表明,仿生优化方法能有效均匀化温度场,但该优化结果对应的温度场的稳定性在一定程度上受太阳光入射角度影响;在温度场均匀化过程中,卫星导热热阻与辐射热阻呈下降趋势,这表明卫星侧表面的传热性能在这一过程中得到了提高。
关键词:卫星;温度场均匀化设计;仿生优化方法;理论;热阻分析
随着空间科学技术的发展,温度场均匀化设计在航天器上获得了越来越多的关注。在卫星热控系统中,温度场均匀化设计尤其重要。对于一般卫星而言,基于轻量化的设计要求,我们需将功率不同的仪器集成到一块仪器板上。要使各仪器在较均衡的温度下工作,就要求温度场有较好的均匀性[1]。在微小卫星方面,整星温度场均匀化设计不仅可以有效避免局部高温或者低温、增加整星的温度稳定性,更能降低热控系统对卫星姿态的要求、提高热控系统的适应能力和调节能力;而且,由于卫星体积小,温度场均匀化设计更容易实现,因而得到了更为广泛的重视[2-3]。对于卫星的辐射散热器而言,温度均匀化设计,尤其是阳光照射较多与较少的辐射器之间的温度均匀化设计,能较大程度的提高辐射器的散热能力[4]。可见,温度场均匀化设计是确保卫星稳定高效运行的有效手段。
目前,研究人员主要采用添加高导热材料、预埋或外贴热管等技术手段达到均匀化温度场的设计目的。考虑成本、重量等因素,高导热材料与热管的使用量会受到限制。因此,在实际应用中需要考虑高导热材料或者热管的优化布置问题。本文针对一个简化的圆柱状卫星模型,考虑填充一定量的高导热材料,对其侧表面温度场进行均匀化设计,对高导热材料的分布进行了优化分析,并基于理论分析了温度场均匀化过程中卫星侧表面的导热热阻和辐射热阻的变化情况,以探讨温度场均匀化过程对其传热性能的影响。
1物理模型
考虑如图1所示的圆柱状卫星,假定其上、下端面绝热,侧表面受阳光照射(太阳常数S=1 367 W/m2)。由于卫星内部各种工作器件会对外传热,且卫星侧表面各部分接受到来自太阳光照射的热量并不均匀,因而卫星侧表面温度场也不均匀,这就有必要对其温度场进行均匀化设计。在均匀化温度场的几种方法中,预埋或者外贴热管实际上相当于填充高导热材料。因此,我们可以只分析填充高导热材料的情况。
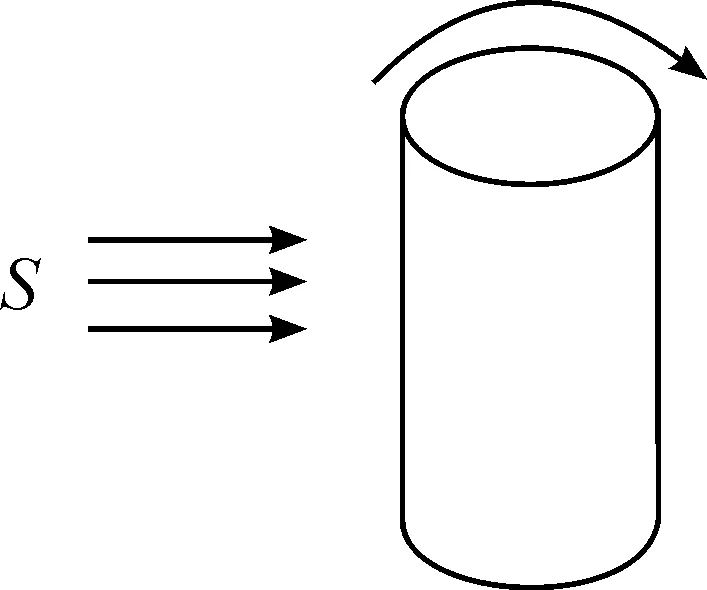
图1 圆柱状卫星示意图
在以下计算分析中,我们设定外太空环境温度T0为4 K,卫星端面圆周长C与圆柱高度H均为0.4 m、侧表面厚度d=0.005 m,侧表面对阳光的吸收率α取0.3、发射率ε取0.8,假设侧表面材料当量导热系数k0=107 W/(mK)、高导热材料的当量热导率kH=1 400 W/(mK)。假定卫星内部器件工作的发热功率P=32 W,并假定这些热量均匀地散发到卫星侧表面上。同时,我们忽略来自地球对卫星的辐射热量以及卫星侧表面在厚度方向上的温度变化。
对于图1所示的卫星,由于假定其上、下端面绝热,因而太阳辐射来的热量与其内部发热最终都将通过其侧表面的热辐射散失掉。同时,在卫星侧表面各部分之间,还存在热量的传导。因此,这是一个热传导和热辐射相耦合的传热问题。如果将卫星的圆柱面沿着太阳光线照射的方向剖开,我们将得到一个二维平面。如果以圆柱周向为x轴方向、圆柱高度方向为y方向,将卫星内部发热、太阳辐射热流以及对外的辐射散热都处理为体热源,我们可以将这个耦合传热问题转化为一个二维平面上的导热问题,其控制方程为:
(1)
其中T为温度,k为热导率,σ为Stefan-Boltzmann常数,β取值与侧表面法向和太阳光入射方向夹角θ相关,有:
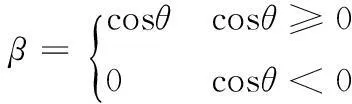
(2)
为衡量卫星侧表面温度场的均匀度,我们定义表明各点温度的均方差为均匀性因子,有[5]:
(3)
其中 f 为温度均匀性因子,A为区域面积,TA为区域平均温度,其计算式为:
TA=∫ATdxdy/A
(4)
可见,f 越小、越接近0,温度场越均匀。
2高导热材料的优化分布
在热传导优化中,“体点问题”[6]是一个获得了较多研究的二维问题。在该问题中,内部存在均匀内热源的“发热体”在四条边界上仅有一个用于导出热量的“低温点”,其余部分的边界均绝热。考虑将给定量的高导热材料填充到“发热体”内,以降低发热体的内部温度。显然,这就存在一个高导热材料如何实现最优分布的问题。为了使“发热体”的平均温度尽可能低,Xia等[7]和Guo等[8]等采用了仿生优化方法来优化高导热材料的分布。按照该方法,高导热材料分两个阶段实现优化分布:第一阶段为高导热材料的“生长”阶段。在该阶段中,首先将给定的区域划分为若干个网格单元,计算得出区域的温度梯度分布,然后在温度梯度最大的那个网格单元上布置高导热材料;布置完成后,重新计算区域的温度梯度分布,再在温度梯度最大的那个网格单元上布置高导热材料,如此循环,直到所有高导热材料均布置到了计算区域内。第二阶段是“进化”和“退化”阶段。在该阶段中,对于区域内温度梯度最大的网格单元,我们采用“进化”过程,在其上布置高导热材料,同时对温度梯度最小的网格单元采用“退化”过程,将布置其上的高导热材料拿掉。如此循环,直到获得稳定的高导热材料分布结果。研究表明,该方法十分有效地降低了“发热体”的平均温度[7-8]。
对于以区域平均温度最低为优化目标的“体点问题”,Guo等[9]通过严格的数学证明得出:区域内最均匀的温度梯度场对应于区域最低平均温度。换言之,区域内温度梯度处处相等时,区域平均温度达到最低。显然,在实施上述仿生优化方法时,在高导热材料的“生长”、“进化”和“退化”过程中,一方面降低了最高的温度梯度,另一方面又提高了最低的温度梯度,因而可以有效地均匀化区域的温度梯度场,从而达到优化传热的目的。进一步,文献[5]将该方法应用到了均匀化区域的温度场中,并分析了温度场均匀化与温度梯度场均匀化之间的关系,结果表明两者有较强的一致性。文[5]的研究表明,添加高导热材料在本质上是减小当地的温度变化,而仿生优化方法始终要求高导热材料布置在温度变化最大的部位,从而减小最大的温度变化,因而这必然可以有效的均匀化温度场。在理想情况下,如果温度场完全均匀,即全场无温差;此时全场温度梯度也等于0,温度梯度场也完全均匀,温度场和温度梯度场的均匀化在此时完全一致。因此,在本文的工作中,我们也采用仿生优化方法对卫星侧表面高导热材料的分布进行优化设计,以实现其温度场的均匀化。
取高导热材料的比重P取10%,我们计算可得高导热材料在卫星侧表面上的分布,如图2所示。在不布置高导热材料之时,温度场均匀性因子 f 为1.07 K,布置之后减小到0.49 K,均匀性提高了54.2%,温度场均匀性得到较大的改善。我们注意到,图2中高导热材料的分布并不呈现对称的结构,这是由于采用仿生优化方法布置高导热材料的选取点方面会产生一定的随机性。例如,在没有布置任何高热导率材料时,考虑对称性可知,沿着y方向的某一条线上的温度梯度都处于最大值,而在这条线上究竟选哪一个点作为布置高热导率材料的第一个点有随机性。这种随机性影响了最后给出的分布结果。

图2 仿生优化方法给出的高导热材料分布
考虑到实际应用的方便,我们可以根据图2的分布进行人工规整,尽量使得高导热材料的分布在周向比较对称,这就可得到图3所示的高导热材料分布。计算可得规整后的f为0.51 K,略高于规整前的结果,这在实际应用中是可以接受的。

图3 规整后的高导热材料分布

由于热量最终通过卫星侧表面的热辐射传递到空间环境中去,我们有必要对辐射传热过程进行分析。在热传导过程中,流的定义为热势(温度)与热流的乘积。考虑到辐射换热过程中,热势不再是温度,而与温度的四次方成正比,因此辐射流率为[14]:
(5)
其中热势U=σT4。这样,我们即可计算辐射耗散率,有[14]:
(6)
其中U0为太空环境的热势。据此,可得卫星侧表面辐射传热的热阻为[14]:
(7)
基于式(6)、式(7),我们以下可以讨论卫星侧表面温度场均匀化与辐射热阻之间的关系。由于卫星总的散热量给定,有:
(8)
根据限制条件式(8),对式(6)求极值,可建立如下泛函:
(9)
其中λ为Lagrange 乘子,且有:
(10)
式(9)所示泛函的Euler公式为:
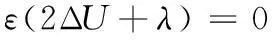
(11)
有:

(12)
将式(10)、式(12)代入式(8)可得:
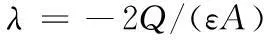
(13)

(14)
可以证明,式(9)对辐射热势差的二阶导数为正,因而式(13)、式(14)使得辐射耗散率取极小值。这就表明,在辐射耗散率取得极小值时,卫星侧表面与太空环境之间的辐射热势差是处处相等的。进一步可见,这实际上意味着卫星侧表面温度场完全均匀。考虑式(7)可知,在本问题中,由于总散热量给定,辐射耗散率越小,则辐射热阻也越小。因此,最小辐射热阻也与均匀的温度场完全对应。
(15)
其中Q为传热量;Gdis-c为导热过程的耗散率,其计算式为:
(16)
由于本问题中热传导的总传热量也是给定的,根据文[9]的论证可知,导热耗散率取得极小值时,区域的温度梯度场是均匀的。考虑式(15)可知,最小的导热热阻也对应于均匀的温度梯度场。
考虑温度场均匀化与温度梯度场均匀化之间存在一定的一致性[5],结合上述分析,可以预测,图1所示卫星侧表面温度场的均匀化必然会减小其辐射热阻,对导热热阻的减小也是有利的。下面,我们用计算来检验这一预测是否正确。通过计算可得,在不布置高导热材料时,导热热阻为8.9×10-3K/W,辐射热阻为7.814 2 m-2;在10%的高导热材料按图2布置后,导热热阻减小到4.2×10-3K/W,辐射热阻减小到7.812 9 m-2。显然,导热热阻与辐射热阻都在减小。为进一步分析温度场均匀化过程中传热热阻的变化情况,我们可计算不同高导热材料填充量之时的热阻变化情况。计算结果与我们用同样方法分析空间辐射器[32]时所得的一样:随着高导热材料填充量的增加,卫星侧表面传热的导热热阻与辐射热阻都呈现减小的趋势;而且,高导热材料的填充量存在阈值,当高导热材料的量超过阈值之后,再增加高导热材料对温度场均匀化的作用不再明显。可见,计算结果表明我们的预测是正确的:卫星侧表面温度场的均匀化有效减小了传热热阻,提高了其传热性能。
4太阳照射角度对温度场均匀性和热阻的影响
对于高导热材料量为10%之时,如果我们采用图3所示的规整布置,那么温度场的均匀性等参数显然会因该布置方案不是完全轴对称的而受阳光入射角度的影响。下面,我们改变太阳照射角度,让阳光从图1中的照射方向沿顺时针垂直于圆柱中心轴旋转一周。在这个过程中,可计算照射光线旋转的弧度φ对热阻和温度均匀性因子的影响,结果如图4、图5所示。可见,随阳光入射角度的变化,热阻与温度均匀性因子都有一定的波动,但图3所示的布置方式仍能较好的改善温度场的均匀性。在对温度场的稳定性要求不高时,采取图3的布置方式是合适的。

图4 太阳光入射角度对热阻的影响
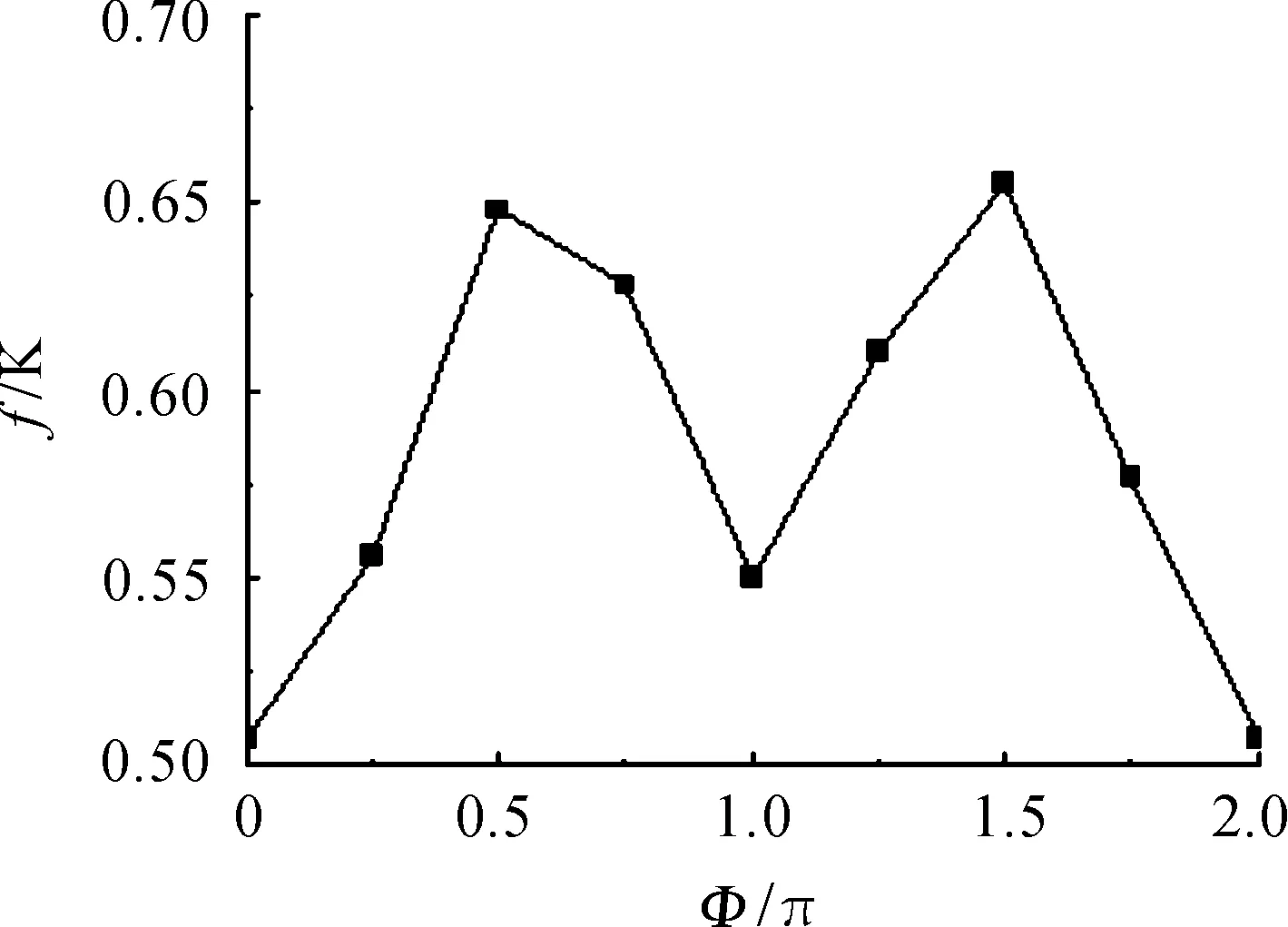
图5 温度均匀性因子随阳光入射角度的变化
考虑到有的应用场合对温度场的稳定性有较高的要求,在这种情况下可采用图6所示的轴对称布置方式。此时,温度场均匀性因子为0.59 K,导热热阻为4.6×10-3K/W,辐射热阻为7.813 1 m-2,较图2、图3的布置方式提高了不少。但此时,各参数不随阳光入射角度的变化而变化,温度场均匀性因子、导热热阻、辐射热阻的提高是为满足温度场稳定性的要求所需付出的代价。

图6 轴对称的布置方式
5结论
本文针对圆柱状卫星的简化模型,采用填充高导热材料的方法对其侧表面进行了温度场均匀化设计,并基于理论分析了温度场均匀化设计过程中的热阻变化情况,讨论了太阳入射角度对卫星侧表面温度场的影响,主要有以下结论:
1)本文采用的仿生优化方法可有效提高卫星侧表面温度场的均匀性,我们可根据其优化结果进行规整以得到便于实用的高导热材料分布方案。
2)在温度场均匀化过程中,卫星侧表面的导热热阻与辐射热阻都呈下降趋势。这表明温度场均匀化过程提升了卫星侧表面的传热性能。
3)根据仿生优化方法的规整结果,在太阳光入射角度发生变化时,温度场均匀性因子和热阻都会有一定的波动,但波动幅度不大。在对温度场稳定性要求不高时,采用这一规整后的分布方案是合适的。在对温度场稳定性要求高时,我们须采用轴对称的分布方案,尽管该方案对应的温度场均匀性因子、导热热阻、辐射热阻均高于仿生优化方法给出的方案。
参考文献:
[1]李卿,王介康,曹亮.FY-2C业务静止气象卫星及发展展望[J].上海航天,2005,22(B12):1-8.
[2]麻慧涛,钟奇,范含林,等.微型卫星热控制技术研究[J].航天器工程,2006,15(2):6-13.
[3]屈金祥.航天器系统热分析综述[J]红外,2004,10:20-27.
[4]周佐新.解决地球静止轨道大容量通信卫星散热的途径[J].航天器工程,2004,13(2):16-19.
[5]CHENG Xuetao,XU Xianghua,LIANG Xingang.Homogenization of temperature field and temperature gradient field[J].Sci.China Ser.E:Tech.Sci.,2009,52(10):2937-2942.
[6]BEJAN A.Constructal-theory network of conducting paths for cooling a heat generating volume[J].Int.J.Heat Mass Transfer,1997,40 (4):779-816.
[7]XIA Zaizhong,LI Zhixin,GUO Zengyuan.Heat conduction:high-conductivity construction based on biological evolution[C].Heat Transfer 2002,Proceeding of the Twelfth International Heat Transfer Conference,2002,2:27-32.
[8]GUO Zengyuan,CHENG Xinguang,XIA Zaizhong.Least dissipation principle of heat transport potential capacity and its application in heat conduction optimization[J].Chin.Sci.Bull.,2003,48(4):406-410.
[9]GUO Zengyuan,ZHU Hongye,LIANG Xingang.Entransy—A physical quantity describing heat transfer ability[J].Int.J.Heat Mass Transfer,2007,50(13):2545-2556.
[10]CHENG Xuetao,LIANG Xingang,GUO Zengyuan.Entransy decrease principle of heat transfer in an isolated system[J].Chin.Sci.Bull.,2011,56(9):847-854.
[11]CHENG Xuetao,LIANG Xingang.Entransy:its physical basis,applications and limitations[J].Chin.Sci.Bull.,2014,59(36):5309-5323.[12]CHEN Lingen.Progress in entransy theory and its applications[J].Chin.Sci.Bull.,2012,57(34):4404-4426.
[13]YUAN Fang,CHEN Qun.Two energy conservation principles in convective heat transfer optimization[J].Energy,2011,36(9):5476-5485.[14]CHENG Xuetao,LIANG Xingang.Entransy flux of thermal radiation and its application to enclosures with opaque surfaces[J].Int.J.Heat Mass Transfer,2011,54(1-3):269-278.
[15]QIAN Xiaodong,LI Zhixin.Analysis of entransy dissipation in heat exchangers[J].Int J Therm Sci,2011,50(4):608-614.
[16]CHENG Xuetao,LIANG Xingang.Optimization principles for two-stream heat exchangers and two-stream heat exchanger networks[J].Energy,2012,46(1):386-392.
[17]WANG Wenhua,CHENG Xuetao,LIANG Xingang.Entransy dissipation,entransy-dissipation-based thermal resistance and optimization of one-stream hybrid thermal network[J].Sci.China:Tech.Sci.,2013,56(2):529-536.
[18]ZHOU Bing,CHENG Xuetao,WANG Wenhua,et al.Entransy analyses of thermal processes with variable thermophysical properties[J].Int.J.Heat Mass Transfer,2015,90:1244-1254.
[19]WANG Wenhua,CHENG Xuetao,LIANG Xingang.Entransy definition and its balance equation for heat transfer with vaporization processes[J].Int.J.Heat Mass Transfer,2015,83:536-544.
[20]CHENG Xuetao,CHEN Qun,HU Guojie,et al.Entransy balance for the closed system undergoing thermodynamic processes[J].Int.J.Heat Mass Transfer,2013,60(1):180-187.
[21]CHENG Xuetao,LIANG Xingang.Entransy loss in thermodynamic processes and its application[J].Energy,2012,44(1):964-972.
[22]YANG Aibo,CHEN Lingen,XIA Shaojun,et al.The optimal configuration of reciprocating engine based on maximum entransy loss[J].Chin.Sci.Bull.,2014,59(17):2031-2038.
[23]CHENG Xuetao,LIANG Xingang.Entransy analyses of heat-work conversion systems with inner irreversible thermodynamic cycles[J].Chin.Phys.B,2015,24(12):120503.
[24]WU Yanqiu.Output power analyses of an endoreversible Carnot heat engine with irreversible heat transfer processes based on generalized heat transfer law[J].2015,24(7):070506.
[25]KIM KH,KIM K.Comparative analyses of energy-exergy-entransy for the optimization of heat-work conversion in power generation systems[J].Int.J.Heat Mass Transfer,2015,84(4):80-90.
[26]BEJAN A.“Entransy”,and its lack of content in physics[J].ASME J.Heat Transfer,2014,136(5):055501.
[27]HERWIG H.Do we really need “entransy”? A critical assessment of a new quantity in heat transfer analysis[J].ASME J Heat Transfer,2014,136(4):045501.
[28]AWAD MM.Discussion:“entransy is now clear”[J].ASME J.Heat Transfer,2014,136(9):095502.
[29]GUO Zengyuan.Closure to Discussion of Entransy,and its lack of content in physics[J].ASME J.Heat Transfer,2014,136(5):056001.
[30]GUO Zengyuan,CHEN Qun,LIANG Xingang.Closure to discussion of do we really need entransy?[J].ASME J.Heat Transfer,2014,136(4):046001.
[31]CHEN Qun,GUO Zengyuan,LIANG Xingang.Closure to discussion of entransy is now clear[J].ASME J.Heat Transfer,2014,136(9):096001.
[32]程雪涛,徐向华,梁新刚.空间辐射器的等温化设计[J].工程热物理学报,2010,31(6):1031-1033.
(责任编辑周江川)
本文引用格式:程雪涛,徐向华,梁新刚.圆柱状卫星侧表面温度场均匀化设计[J].兵器装备工程学报,2016(5):1-6.
Citation format:CHENG Xue-tao,XU Xiang-hua,LIANG Xin-gang.Homogenization Design of Temperature Field for the Side Surface of a Cylindrical Satellite[J].Journal of Ordnance Equipment Engineering,2016(5):1-6.
Homogenization Design of Temperature Field for the Side Surface of a Cylindrical Satellite
CHENG Xue-tao,XU Xiang-hua,LIANG Xin-gang
(School of Aerospace,Tsinghua University,Beijing 100084,China)
Abstract:The homogenization design of temperature field has attracted more and more attentions because it is beneficial to the stable and effective operation of spacecrafts.In this paper,the distribution of the limited high conductivity material was optimized by the bionic optimization method to homogenize the temperature field of the side surface of a simplified cylindrical satellite.At the same time,the variations of the conductive thermal resistance and the radiative thermal resistance during the homogenization were also analyzed with the entransy theory.The affection from the incident angle of the sunlight was also discussed.The results show that the bionic optimization method is effective for the homogenization design,but the stability of the temperature field corresponding to the optimization result would be affected by the incident angle of the sunlight to some extent.During the homogenization process,both the conductive thermal resistance and the radiative thermal resistance decrease.Therefore,the heat transfer performance of the side surface is improved in the process.
Key words:satellite; homogenization design of temperature field; bionic optimization method; entransy theory; thermal resistance analysis
doi:【审稿专家特稿】10.11809/scbgxb2016.05.001
收稿日期:2016-01-20;修回日期:2016-02-10
基金项目:国家自然科学基金(51376101)
作者简介:程雪涛(1983—),男,博士,助理研究员,本刊审稿专家,主要从事航天器热管理、新概念热学等方面的研究工作。
中图分类号:TJ8;V520.6;TK11
文献标识码:A
文章编号:2096-2304(2016)05-0001-06

