不平衡电网电压下模块化多电平换流器的环流抑制策略

梁营玉　张　涛　刘建政　杨奇逊　刘　树

(1.新能源电力系统国家重点实验室(华北电力大学)　北京　102206 2.北京四方继保自动化股份有限公司　北京　100085 3.电力系统及发电设备控制和仿真国家重点实验室(清华大学)　北京　100084)



不平衡电网电压下模块化多电平换流器的环流抑制策略

梁营玉1张涛2刘建政3杨奇逊1刘树2

(1.新能源电力系统国家重点实验室(华北电力大学)北京102206 2.北京四方继保自动化股份有限公司北京100085 3.电力系统及发电设备控制和仿真国家重点实验室(清华大学)北京100084)

摘要模块化多电平换流器(MMC)内部环流的存在增大了桥臂电流的峰值和有效值，增加了子模块电容电压的波动幅度，影响电力电子器件的安全运行，因此，有必要对其进行有效抑制。通过对相单元瞬时能量进行推导和分析，指出电网电压不平衡时三相环流可能存在2倍频的正序、负序和零序分量，三相环流的直流分量不一定彼此相等。推导了三相环流直流分量即环流参考值的计算公式，并提出基于比例积分(PI)调节器和矢量比例积分(VPI)调节器并联的新型环流抑制策略，给出了相关控制参数的整定方法。新型环流抑制策略可直接在abc三相静止坐标系下执行，因而无需坐标变换和锁相环，控制结构简单，可同时消除2倍频正序、负序和零序环流，并且在电网电压平衡和不平衡时均适用。在PSCAD/EMTDC中搭建了21电平MMC仿真模型，验证了该环流抑制策略的正确性和有效性。

关键词：环流抑制电网电压不平衡矢量比例积分模块化多电平换流器

0引言

模块化多电平换流器(Modular Multilevel Converter，MMC)作为一种新型的电压源换流器(Voltage Source Converter，VSC)，具有模块化设计、扩展性好、开关频率低、波形质量好等优点，近年来得到广泛关注[1]。良好的可扩展性使得MMC更适合中、高压应用场合，在高压直流输电领域获得越来越多的应用[2]。

与传统的两电平或三电平电压源换流器不同，MMC的储能电容并不集中安装在公共直流母线上，而是分散安装在各子模块中。MMC各相单元瞬时电压不同导致相单元之间产生内部环流，环流会引起桥臂电流畸变，并增大其峰值和有效值，从而导致桥臂损耗增加，并且危及电力电子器件和储能电容的安全运行[3，4]。因此，抑制MMC环流具有重要意义。

电网电压平衡时，三相环流为2倍频的负序分量，三相环流相互抵消，只在3个相单元之间流通，因此并不影响MMC的直流侧。而电网电压不平衡时，除了负序分量外，还将出现2倍频的正序和零序分量。三相环流的零序分量将流入直流侧导致直流电流产生波动，并通过直流传输线路传播到其他换流站，影响其他换流站的正常运行[5-7]。电网电压不平衡时的环流抑制策略是MMC控制的一个难点。适当增加桥臂电感可以在一定程度上降低环流大小，但并不能彻底消除环流[8，9]。同时由于高压电感的价格昂贵，使得该方法的经济性较差，并且较大的桥臂电感将影响MMC的动态性能。文献[5]采用2倍频负序旋转坐标变换将三相环流转换为直流量，使用PI调节器对其进行控制。该方法只能抑制负序环流，因而在电网电压不平衡时的控制效果不理想。文献[10]提出基于2倍频陷波器和准比例谐振(Proportional Resonance，PR)调节器的abc静止坐标系下的环流抑制策略，在电网电压平衡和不平衡时均取得良好的环流抑制效果，但2倍频陷波器的引入降低了控制系统的响应速度。文献[7]提出一种基于三相静止坐标下PIR调节器的环流抑制方法，该方法采用4个PIR调节器，其中3个PIR调节器用于控制正序和负序环流，一个PIR调节器用于控制零序环流。该方法虽然能同时控制正序、负序和零序环流，但其控制结构较为复杂。

本文首先介绍了MMC的拓扑结构和数学模型；然后对电网电压不平衡时的相单元瞬时能量进行了理论推导和详细分析，指出电网电压不平衡时可能存在2倍频正序、负序和零序环流；然后给出了环流直流分量即环流参考值的计算公式，指出电网电压不平衡时三相环流直流分量不一定彼此相等，提出基于PI调节器与VPI调节器并联的控制结构，给出相关控制参数的整定方法和原则；最后，在PSCAD/EMTDC中搭建了21电平MMC仿真模型，对本文所提环流抑制策略进行了验证。

1MMC拓扑结构和数学模型

1.1拓扑结构

三相MMC的电路结构如图1所示。三相MMC由6个相同的桥臂构成，上、下两个桥臂组成一个相单元，每个桥臂由N个完全相同的半桥子模块(Sub-Module，SM)和一个桥臂电感Lr串联而成。正常运行时，子模块有两种互补的状态：当绝缘栅双极晶体管(Insulated Gate Bipolar Transistor，IGBT)VT1导通、VT2关断时，SM处于投入状态，SM的输出电压等于储能电容电压UC；当VT1关断，而VT2导通时，SM处于切除状态，SM的输出电压等于0。

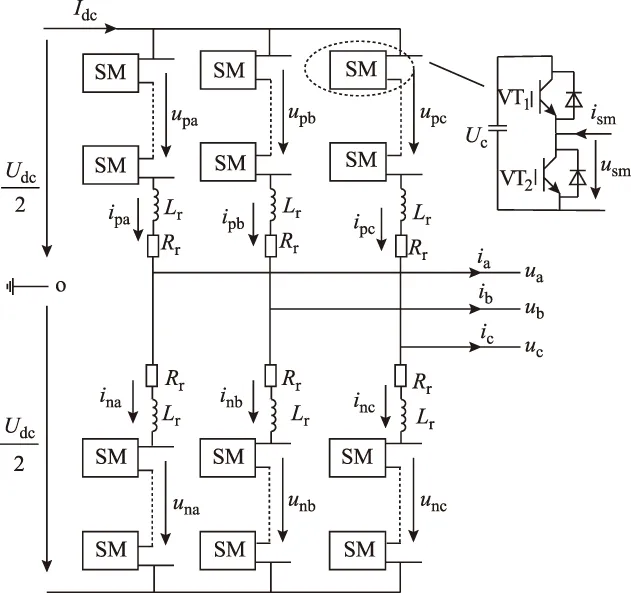
图1　三相MMC拓扑Fig.1　Three phase MMC topology

图1中，Lr为桥臂电感；Rr为桥臂等效损耗电阻；Udc和Idc分别为直流电压和直流电流；uj和ij分别为j相电压和电流；upj和unj分别为j相上桥臂电压和下桥臂电压，其中p代表上桥臂，n代表下桥臂；ipj和inj分别为j相上桥臂电流和下桥臂电流；其中j=a，b，c。

1.2数学模型

根据MMC的电路结构和基尔霍夫定律可得[11]

(1)

(2)

式中，udiffj为MMC的内部不平衡电压，j=a,b,c；ej为MMC的j相输出电压，其表达式为

(3)

idiffj为内部环流，其表达式为

(4)

根据式(2)和式(3)，上、下桥臂的参考电压可由式(5)和式(6)获得。

(5)

(6)

式中，ej由MMC交流侧的电流环控制器得到；udiffj由环流抑制控制器得到[12，13]。

2不平衡电网电压下相单元瞬时能量分析

由于MMC的换流变压器一般采用Y/△接线，因此，暂不考虑零序分量。电网电压不平衡时，ea和ia均可分解为正序分量和负序分量，其表达式为

ea=E+cos(ω0t+θ+)+E-cos(ω0t+θ-)

(7)

ia=I+cos(ω0t+φ+)+I-cos(ω0t+φ-)

(8)

式中，ω0为电网角频率；E+、E-分别为正序和负序电压的幅值；θ+、θ-分别为正负和负序电压的初相角；I+、I-分别为正序和负序电流的幅值；φ+、φ-分别为正负和负序电流的初相角。

假设在udiffj的作用下，环流的交流量被完全消除，则上、下桥臂电流可表示为

(9)

(10)

式中，Idca为a相环流的直流分量。

根据式(5)、式(6)、式(9)、式(10)可得相单元a的瞬时功率表达式为

pa=upaipa+unaina=eaia+(Udc-2udiffa)Idca

(11)

由于udiffa≪Udc，为了便于分析，忽略udiffa，式(11)可简化为

pa=upaipa+unaina=eaia+UdcIdca

(12)

将式(5)～式(10)代入式(12)可得

(13)

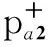
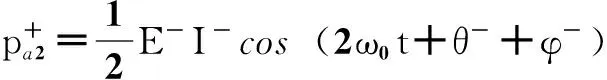
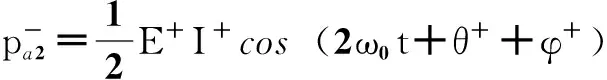
E-I+cos(2ω0t+θ-+φ+)]

对式(13)积分，可得相单元a的瞬时能量Wa的表达式为

(14)

同理，可得到相单元b和c的瞬时能量表达式分别为

(15)

(16)

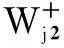
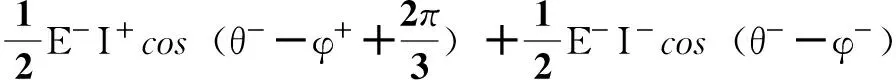
E-I+sin(2ω0t+θ-+φ+)]

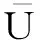
若pj0≠0(j=a，b，c)，则相单元j的瞬时能量将随时间不断增加(pj0>0)或不断减小(pj0<0)，从而导致系统不稳定。因此稳态时，pj0应等于0，即满足式(17)。

pa0=pb0=pc0=0

(17)

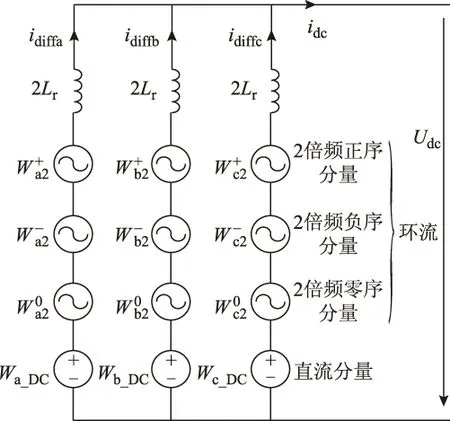
图2　不平衡电网电压下MMC三相瞬时能量等效电路Fig.2　Three phase instantaneous energy equivalent circuit of an MMC under unbalanced grid voltage

理想电网下，电压和电流均不存在负序分量，即E-=0,I-=0，则

(18)

因此，电网电压平衡时仅存在2倍频负序环流。

电网电压不平衡时，若采用抑制负序电流的控制目标，即E-≠0,I-=0，则

(19)

因此，环流中存在2倍频负序和零序分量，不存在正序分量。

电网电压不平衡时，若采用抑制有功波动或无功波动的控制目标，即E-≠0,I-≠0，则

(20)

环流中同时存在2倍频正序、负序和零序分量。

虽然在不同情况下内部环流会出现不同分量，但为了能在各种情况下有效抑制所有环流分量，避免环流对MMC正常运行时的影响，制定的环流抑制策略应能同时消除2倍频正序、负序和零序分量。

3电网电压不平衡时的环流抑制策略

3.1环流参考值的计算

由式(17)可得到三相环流的直流分量表达式，如式(21)～式(23)所示。

(21)

(22)

(23)

由式(21)～式(23)可看出，电网电压不平衡时，三相环流的直流分量并不一定彼此相等，即直流电流在三相桥臂中并不一定平均分配。令Idca=Idcb=Idcc，可得

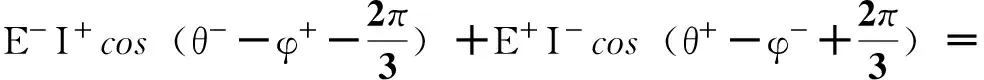
(24)

当且仅当式(24)成立时，三相环流的直流分量彼此相等，等于直流电流的1/3。

理想电网下，满足E-=0, I-=0，式(24)显然成立，因此

(25)

电网发生不对称故障时，为了保证三相电流对称，并且防止电力电子器件的过电流，一般采用抑制负序电流的控制策略，满足E-≠0,I-=0，显然式(24)不成立。因此，三相环流直流分量彼此不相等。

环流主要由直流分量和2倍频交流分量组成，直流分量用于有功功率的传输，故环流抑制的目标为消除2倍频交流分量而保留直流分量。因此，式(21)～式(23)计算得到的直流量即为三相环流的参考值。

3.2环流抑制策略的设计

为了消除电网电压不平衡时出现的2倍频正序、负序和零序环流分量，本文提出一种abc静止坐标系下的新型环流抑制策略，如图3所示。采用PI调节器和VPI调节器[14-16]并联的控制结构，PI调节器和VPI调节器的传递函数分别如式(26)和式(27)所示。

(26)

(27)

式中，kp1和ki1分别为PI调节器的比例增益和积分增益；kp2和ki2分别为VPI调节器的比例增益和积分增益。

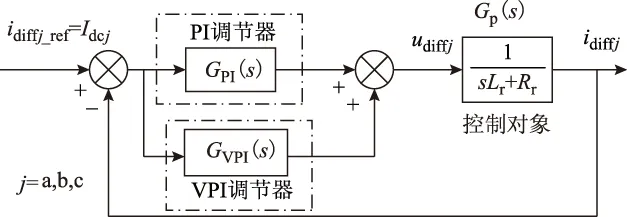
图3　环流抑制策略控制框图Fig.3　Block diagram of the proposed circulating current suppressing scheme

PI调节器的积分环节可以保证对直流参考值Idcj的无静差跟踪，比例环节主要用于提高控制系统的响应速度；VPI调节器在谐振频率处的增益理论上为无穷大，可以对谐振频率处的信号实现无静差跟踪控制，为了抑制2倍频环流，本文取谐振频率为2ω0。PI调节器和VPI调节器的幅频特性曲线如图4所示。PI调节器用于控制直流量，其在0 Hz处的增益较大，而VPI调节器在0 Hz处的增益非常小，因此VPI调节器几乎不影响PI调节器对直流量的调节作用。同理，VPI调节器用于抑制2倍频(100 Hz)环流，其在100 Hz处的增益非常大，而PI调节器对100 Hz处的增益相对较小，因此PI调节器几乎不影响VPI调节器对2倍频分量的调节作用。由上述分析可知，两种电流调节器彼此间的影响较小，可认为PI与VPI调节器相互不受影响，因此，可独立整定各自的控制参数。

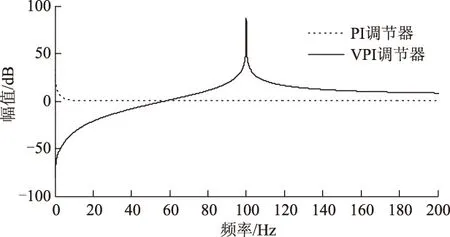
图4　PI调节器和VPI调节器的幅频特性曲线Fig.4　Magnitude frequency characteristic curves of PI regulator and VPI regulator

3.3PI和VPI调节器的设计

由式(27)可知，VPI调节器的分子项为一个二阶环节，通过设置适当的控制参数kp2和ki2，可以使VPI调节器的极点与控制对象的零点相消，以实现闭环传递函数在谐振频率处0 dB增益和0°相位响应，提高了对谐振频率信号控制的精度和稳定性[17]。而PIR调节器中谐振部分的分子为一阶环节，无法实现闭环传递函数在谐振频率点处的0 dB增益和0°相位响应[18]，因此本文采用VPI调节器进行2倍频环流分量抑制。为实现零极点对消，控制参数kp2和ki2与桥臂电感Lr和桥臂电阻Rr应满足式(28)。

(28)

仅考虑VPI调节器时，闭环传递函数为

(29)

由式(29)可看出，零极点对消后的闭环传递函数为一个二阶带通滤波器，滤波器的带宽为kp2/(πLr) Hz。图5为kp2分别取0.1、0.3和0.5时的闭环传递函数伯德图。由图5可知，无论kp2如何变化，闭环传递函数在100 Hz处始终具有0 dB增益和0°相位，保证了对100 Hz环流的无静差控制。当频率偏离100 Hz后，闭环传递函数的增益迅速下降，从而保证了良好的频率选择性。随着kp2的增加，闭环传递函数的带宽增加，从而提高了对电网频率变化的鲁棒性；而较大的带宽降低了对频率的选择性。因此，kp2的选择将直接决定闭环传递函数的性能。

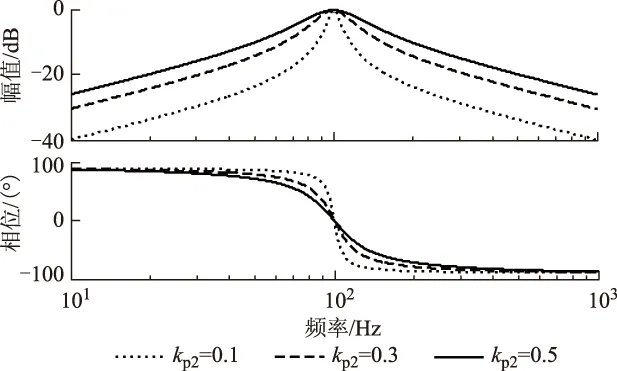
图5　仅考虑VPI调节器时的闭环传递函数伯德图Fig.5　Bode diagram of closed loop transfer function when considering only the VPI regulator

电网的频率一般在±0.5 Hz以内，为保留一定的裕度，假设电网频率最大允许偏差为±1 Hz。则kp2应满足如下限制条件

kp2≥2πLr

(30)

kp2满足式(30)即可保证对电网频率变化的鲁棒性，同时为了兼顾对频率良好的选择性，kp2应尽量取较小的值，因此本文取式(30)的下限2πLr。ki2可根据kp2及式(28)取值。

根据3.1节的分析可知，整定PI参数时可不考虑VPI调节器。仅考虑PI调节器时，闭环传递函数为

(31)

借鉴VPI调节器的参数选取方法，控制参数kp1和ki1与桥臂电感Lr和桥臂电阻Rr应满足式(32)。

(32)

将式(32)代入式(31)，通过零极点对消，二阶闭环传递函数变为一阶惯性环节为

(33)

式中，Ti为一阶惯性环节的时间常数，Ti=Lr/kp1，Ti代表了闭环传递函数的响应速度，一般取0.5～5 ms[19]，Ti的值确定后，通过Ti的表达式可得到kp1，然后通过式(32)可得到ki1。

4仿真结果与分析

为验证本文所提的环流抑制策略，在PSCAD/EMTDC中搭建如图6所示的仿真模型，相应的仿真参数如表1所示。图7为仿真中采用的MMC整体控制框图。采用双dq-PI控制MMC交流侧的正、负序电流，正序电流指令值根据有功、无功指令值通过相关公式计算得到；为了消除负序电流，将负序电流的指令值设为0。双dq-PI控制策略[7，20]产生的指令电压ejref和本文所提环流抑制策略产生的指令电压udiffj_ref按照图7中的规则进行合成即得到上、下桥臂的调制电压upjref、unj；然后经过NLM调制和子模块电容电压平衡策略最终得到上、下桥臂IGBT的触发信号。

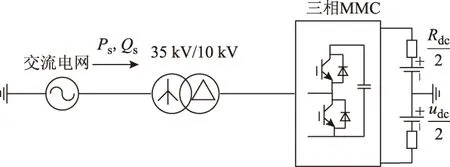
图6　MMC仿真模型Fig.6　Simulation model for MMC

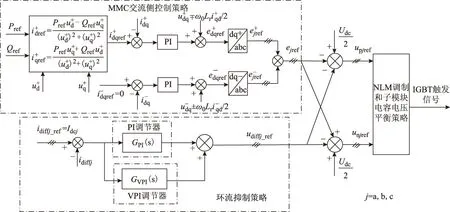
图7　MMC整体控制框图Fig.7　Block diagram of MMC overall control strategy

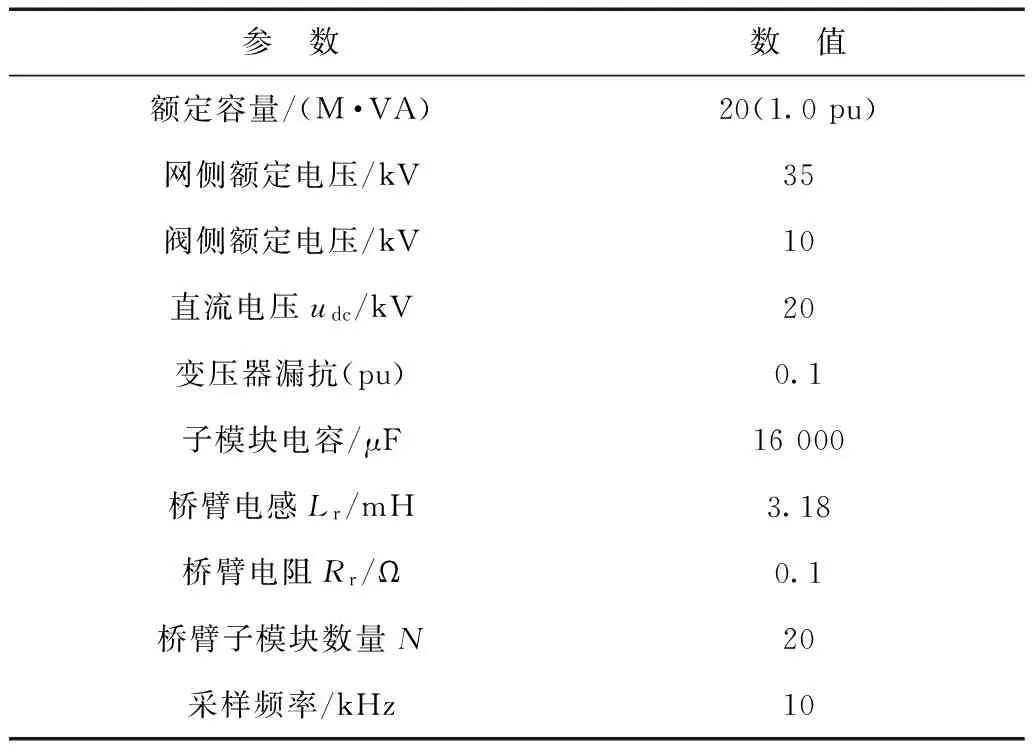
参 数数 值额定容量/(M·VA)20(1.0pu)网侧额定电压/kV35阀侧额定电压/kV10直流电压udc/kV20变压器漏抗(pu)0.1子模块电容/μF16000桥臂电感Lr/mH3.18桥臂电阻Rr/Ω0.1桥臂子模块数量N20采样频率/kHz10

4.1电网电压平衡时仿真分析

在电网电压平衡时对本文所提的环流抑制策略进行测试，仿真结果如图8所示。其中，图8a为网侧三相电压波形；图8b为换流变压器网侧有功和无功功率波形；图8c为MMC交流侧三相电流波形；图8d为A相上、下桥臂电流波形；图8e为三相环流波形；图8f为 A相上桥臂子模块电容电压波形；图8g为直流电流波形。

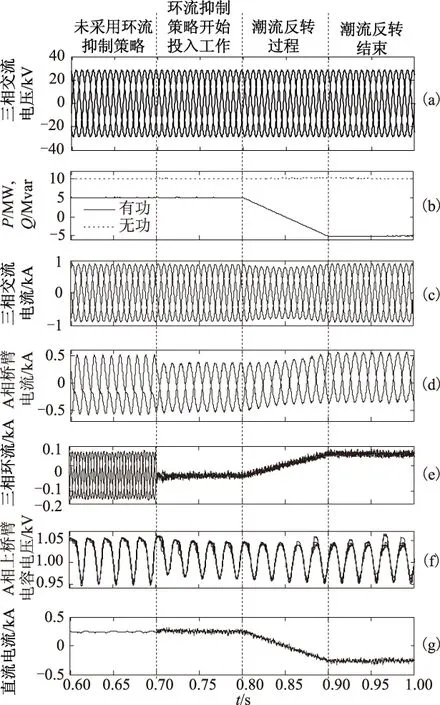
图8　环流抑制效果波形Fig.8　Waveforms of circulating current suppressing effect

0.6～0.7 s期间，未采用环流抑制策略，由于2倍频负序环流的存在导致A相上、下桥臂电流存在严重的畸变(图8d)，总谐波畸变率(Total Harmonic Distortion，THD)约为41.2%。0.7 s时，环流抑制策略开始投入工作，2倍频环流得到有效抑制(图8e)，A相上、下桥臂电流变为较理想的正弦波(图8d)，波形质量得到明显改善，并且桥臂电流的峰值和有效值都有所降低，从而降低了桥臂的损耗，并提高了MMC运行的安全性。2倍频环流消除后，子模块电容电压(图8f)的波动幅度也随之减小。0.8～0.9 s期间进行潮流反转测试，有功功率由5 MW逐渐变为0 MW，再由0 MW逐渐变为-5 MW(图8b)，三相交流电流随有功功率的变化逐渐减小，然后再逐渐增大(图8c)，无功功率始终为10 Mvar。潮流反转期间，环流抑制策略仍具有良好的控制效果，三相环流仅含有直流分量(图8e)。潮流反转后，直流电流的方向也发生反转(图8g)。由图8e可看出，电网电压平衡时，三相环流的直流分量始终保持彼此相等即Idca=Idcb=Idcc，与理论分析结果一致。

4.2电网电压不平衡时仿真分析

为了验证本文所提环流抑制策略在不平衡电网电压下的有效性以及相对于传统环流抑制策略(CCSC)的优越性，图9给出了采用文献[5]所提环流抑制策略(CCSC)时的仿真结果，图10给出了采用本文所提环流抑制策略时的仿真结果。

0.6 s时，B相电压发生50%的电压跌落导致三相电压不平衡，采用抑制负序电流的控制策略，因此，交流电流保持三相平衡(图9c、图10c)。虽然消除了负序电流，但由于负序电压的存在使得有功和无功功率出现2倍频的波形分量(图9b、图10b)。电网电压不平衡导致三相环流不平衡(图9d、图10d)，除了2倍频负序分量外，还出现了零序分量。三相环流中的2倍频负序分量相互抵消，并不会流通到直流侧；而零序分量将流通到直流侧引起直流电流出现较大的波形(图9f、图10f)，若波动的直流电流通过直流线路传播到对端换流站，将影响其正常运行。

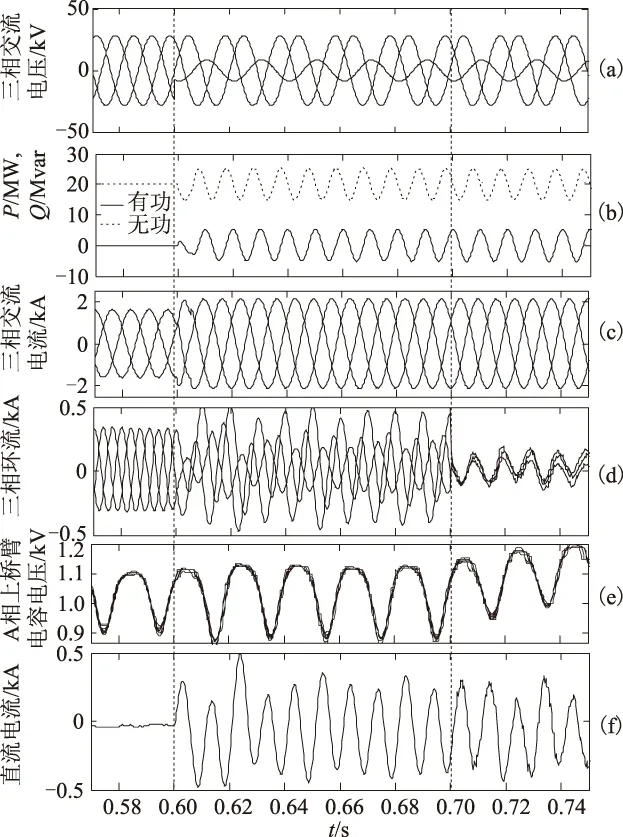
图9　文献[5]提出的CCSC方法的仿真结果Fig.9　Simulation results of the CCSC in literature[5]

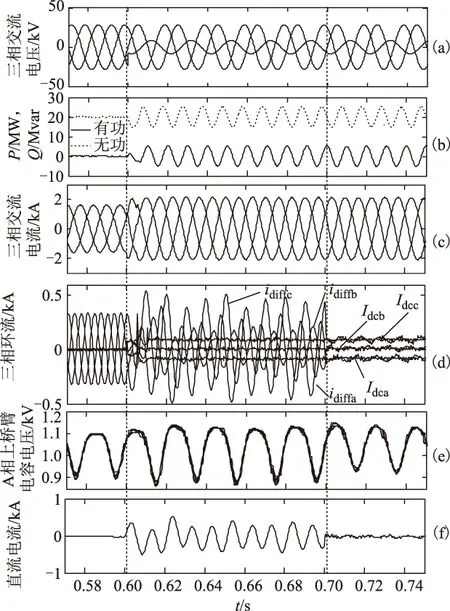
图10　本文所提环流抑制策略的仿真结果Fig.10　Simulation results of the proposed circulating suppressing method

0.7 s时，环流抑制策略开始投入工作，文献[5]提出的CCSC只能消除2倍频负序环流，因此，三相环流中仍存在2倍频零序环流(图9d)，导致直流电流仍存在波动(图9f)。而采用本文所提的环流抑制策略后，不仅消除了2倍频负序环流，2倍频零序环流也得到有效抑制，三相环流准确跟踪上其参考值即直流分量(图10d)。由于消除了2倍频零序环流，直流电流的波动分量也随之消失，变为理想的直流量(图10f)。综上所述，本文所提的环流抑制策略控制效果明显优于CCSC。如图9d所示，电网电压不平衡时，三相环流的直流分量彼此不相等即Idca≠Idcb≠Idcc，与3.1节的理论分析结果一致。

5结论

本文提出一种电网电压不平衡时的新型环流抑制策略，由环流参考值计算环节和环流参考值电流跟踪环节组成。通过分析电网电压不平衡时相单元瞬时能量，指出电网电压不平衡时三相环流可能存在2倍频正序、负序和零序分量，其直流分量并不一定彼此相等，并给出环流直流分量即环流参考值的计算公式，然后采用PI调节器与VPI调节器并联的控制结构进行直流参考电流的跟踪和2倍频正序、负序和零序环流的抑制。该策略可以在abc三相静止坐标系下直接执行，无需坐标变换和锁相环，不需要将2倍频环流的正序、负序和零序分量进行分离，控制结构较简单，易于执行。

在PSCAD/EMTDC中搭建21电平MMC仿真模型，在电网电压平衡和不平衡时对本文所提环流抑制策略进行验证，并与CCSC的仿真结果进行对比。仿真结果表明，本文所提的环流抑制策略在电网电压平衡和不平衡时均取得良好的控制效果，并且电网电压不平衡时控制效果明显优于CCSC。

参考文献

[1]孔明，汤广福，贺之渊，等.不对称交流电网下MMC-HVDC输电系统的控制策略[J].中国电机工程学报，2013，33(28)：41-49.

Kong Ming，Tang Guangfu，He Zhiyuan，et al.A control strategy for modular multilevel converter based HVDC of unbalanced AC systems[J].Proceedings of the CSEE，2013，33(28)：41-49.

[2]Deng F，Chen Z.A control method for voltage balancing in modular multilevel converters[J].IEEE Transactions on Power Electronics，2014，29(1)：66-76.

[3]Li Z，Wang P，Chu Z，et al.An inner current suppressing method for modular multilevel converters[J].IEEE Transactions on Power Electronics，2013，28(11)：4873-4879.

[4]Li Shaohua，Wang Xiuli，Yao Zhiqing，et al.Circulating current suppressing strategy for MMC-HVDC based on nonideal proportional resonant controllers under unbalanced grid conditions[J].IEEE Transactions on Power Electronics，2015，30(1)：387-397.

[5]Tu Qingrui，Xu Zheng，Xu Lie.Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters[J].IEEE Transactions on Power Delivery，2011，26(3)：2009-2017.

[6]Zhou Y，Jiang D，Guo J，et al.Analysis and control of modular multilevel converters under unbalanced conditions[J].IEEE Transactions on Power Delivery，2013，28(4)：1986-1995.

[7]Moon J W，Kim C S，Park J W，et al.Circulating current control in MMC under the unbalanced voltage[J].IEEE Transactions on Power Delivery，2013，28(3)：1952-1959.

[8]Tu Qingrui，Xu Zheng，Huang H，et al.Parameter design principle of the arm inductor in modular multilevel converter based HVDC[C]//2010 International Conference on Power System Technology，Hangzhou，China，2010：1-6.

[9]屠卿瑞，徐政，郑翔，等.模块化多电平换流器型直流输电内部环流机理分析[J].高电压技术，2010，36(2)：547-552.Tu Qingrui，Xu Zheng，Zheng Xiang，et al.Mechanism analysis on the circulating current in modular multilevel converter based HVDC[J].High Voltage Engineering，2010，36(2)：547-552.

[10]班明飞，申科，王建赜，等.基于准比例谐振控制的MMC 新型环流抑制器[J].电力系统自动化，2014，38(11)：85-89，129.

Ban Mingfei，Shen Ke，Wang Jianze，et al.A novel circulating current suppressor for modular multilevel converters based on quasi-proportional-resonant control[J].Automation of Electric Power Systems，2014，38(11)：85-89，129.

[11]Antonopoulos A，Angquist L，Nee H P.On dynamics and voltage control of the modular multilevel converter[C]//13th European Conference on Power Electronics and Applications，Barcelona，Spain，2009.

[12]Tu Qingrui，Xu Zheng，Chang Yong，et al.Suppressing DC voltage ripples of MMC-HVDC under unbalanced grid conditions[J].IEEE Transactions on Power Delivery，2012，27(3)：1332-1338.

[13]Shi Xiaojie，Wang Zhiqiang，Liu Bo，et al.Characteristic investigation and control of a modular multilevel converter-based HVDC system under single-line-to-ground fault conditions[J].IEEE Transactions on Power Electronics，2015，30(1)：408-421.

[14]Lascu C，Asiminoaei L，Boldea I，et al.High performance current controller for selective harmonic compensation in active power filters[J].IEEE Transactions on Power Electronics，2007，22(5)：1826-1835.

[15]Mwasilu F，Justo J J，Ro K S，et al.Improvement of dynamic performance of doubly fed induction generator-based wind turbine power system under an unbalanced grid voltage condition[J].IET Renewable Power Generation，2012，6(6)：424-434.

[16]Trinh Q N，Lee H H.An advanced current control strategy for three-phase shunt active power filters[J].IEEE Transactions on Industrial Electronics，2013，60(12)：5400-5410.

[17]年珩，沈永波，宋亦鹏.不平衡及谐波电网电压下并网逆变器的直接功率控制策略[J].电网技术，2014，38(6)：1452-1458.

Nian Heng，Shen Yongbo，Song Yipeng.Direct power control strategy of grid connected inverter under unbalanced and harmonic grid voltage[J].Power System Technology，2014，38(6)：1452-1458.

[18]年珩，宋亦鹏.谐波电网下基于矢量比例积分电流调节器的双馈异步发电机运行控制技术[J].中国电机工程学报，2013，33(6)：101-111.

Nian Heng，Song Yipeng.DFIG operation control strategy under distorted grid conditions based on VPI current regulators[J].Proceedings of the CSEE，2013，33(6)：101-111.

[19]Yazdani A，Iravani R.Dynamic model and control of the NPC-based back-to-back HVDC system[J].IEEE Transactions on Power Delivery，2006，21(1)：414-424.

[20]章玮，王宏胜，任远，等.不对称电网电压下三相并网型逆变器的控制[J].电工技术学报，2010，25(12)：103-110.

Zhang Wei，Wang Hongsheng，Ren Yuan，et al.Investigation on control of three-phase grid-connected inverters under unbalanced grid voltage conditions[J].Transactions of China Electrotechnical Society，2010，25(12)：103-110.

作者简介

梁营玉男，1989年生，博士研究生，研究方向为HVDC和柔性交流输配电技术。

E-mail：liangyingyu2013@163.com(通信作者)

张涛男，1971年生，教授级高工，研究方向为电力系统保护与控制、电力电子在电力系统中的应用、新能源并网等。

E-mail：zhangtao@sf-auto.com

A Circulating Current Suppressing Method for Modular Multilevel Converter Under Unbalanced Grid Voltage

Liang Yingyu1Zhang Tao2Liu Jianzheng3Yang Qixun1Liu Shu2

(1.State Key Laboratory for Alternate Electrical Power System With Renewable Energy Sources North China Electric Power UniversityBeijing102206China 2.Beijing Sifang Automation Co.LtdBeijing100085China 3.State Key Laboratory of Control and Simulation of Power Systems and Generation Equipments Tsinghua UniversityBeijing100084China)

AbstractThe circulating current within modular multilevel converters increases the peak/RMS value of the arm currents and the magnitude of the sub-module voltage fluctuation，and thus affects the safe operation of power electronic devices.Therefore，it is necessary to eliminate the circulating current.It is pointed that，under the unbalanced grid voltage，the second three-phase harmonic circulating current can be decomposed into positive，negative and，zero sequence components and the dc component of the three-phase circulating current is not necessary equal to each other by deriving and analyzing the phase unit instantaneous energy.The formulas of the dc component of the circulating current，i.e.the circulating current reference，are derived and a novel circulating current suppressing method，which is based on proportional-integral (PI) regulator and vector proportional-integral (VPI) regulator in parallel，is proposed.The tuning principle of the related control parameters is given.The novel circulating current suppressing method can be executed in the abc stationary reference frame so that coordinate transformation is not needed and thus it has a simple control structure.Besides that，the positive，negative，and zero sequence components of the second harmonic circulating current can be eliminated simultaneously and the method can achieve good control performance under balanced and unbalanced grid voltages.A 21-level MMC simulation model is set up in the PSCAD/EMTDC in order to validate the correctness and effectiveness of the proposed method.

Keywords：Circulating current suppression，unbalanced grid voltage，vector proportional-integral，modular multilevel converter

中图分类号：TM721.1

收稿日期2015-03-19改稿日期2015-04-18