基于经验模态分解和核主成分分析的SAR图像相干斑抑制
李长超,王文波
(1.武汉科技大学计算机科学与技术学院,湖北 武汉,430065;2.武汉科技大学智能信息处理与实时工业系统湖北省重点实验室,湖北 武汉,430065;3.武汉科技大学理学院,湖北 武汉,430065)
基于经验模态分解和核主成分分析的SAR图像相干斑抑制
李长超1,2,王文波3
(1.武汉科技大学计算机科学与技术学院,湖北 武汉,430065;2.武汉科技大学智能信息处理与实时工业系统湖北省重点实验室,湖北 武汉,430065;3.武汉科技大学理学院,湖北 武汉,430065)
摘要:结合经验模态分解(EMD)与核主成分分析(KPCA)方法,针对SAR图像提出一种改进的相干斑抑制算法。首先将SAR图像进行对数变换和均值调整后进行经验模态分解;然后利用KPCA进一步去除各层本征模态函数(IMF)中的噪声,具体方法是根据斑点噪声的统计特性和零均值高斯白噪声IMF的能量分布模型,近似计算各层 IMF中噪声能量所占比例,据此选择合适数量的主成分重构IMF;最后对经过KPCA处理的IMF进行累加重构得到去噪SAR图像。实验结果表明, 与另外两种EMD图像去噪算法相比,本文提出的方法在相干斑抑制效果和图像细节信息保持能力两方面都有较好的提高。
关键词:SAR图像;相干斑抑制;经验模态分解;核主成分分析;本征模态函数;图像去噪
合成孔径雷达(SAR)图像会受到自身固有的相干斑噪声的影响,这些在SAR图像中随机散布的相干斑与较小的地物目标混杂在一起,严重影响图像质量,对图像的自动解译造成很大困难[1-2]。基于小波变换的SAR图像相干斑抑制算法具有较好的滤波效果[3-5],但其需要预先设定小波基和分解层数,不同的设定会对图像去噪效果产生决定性的影响。目前,如何选择最优小波和最优分解层数仍是一个难题。
经验模态分解(empirical mode decomposition, EMD)[6-7]为SAR图像相干斑抑制提供了一种新的思路。EMD将信号分解成有限个本征模态函数(intrinsic mode function,IMF)和一个均值趋势函数。在利用EMD进行信号分解时,不再需要凭经验预先设定基函数和分解层数,而是根据信号自身的特性自适应地产生基底并确定最优分解层数。对于非线性和非稳态信号,EMD更能反映信号所包含的本质特征, 其性能要优于小波分解[6]。SAR图像属于典型的非线性和非稳态信号,EMD在SAR图像相干斑抑制中已经获得了较好的应用效果[8-11]。利用EMD部分重构方法对SAR图像去噪的一般步骤是:首先对SAR图像进行EMD分解,然后将高频IMF当作噪声直接去除,将剩余的IMF作为信号进行累加从而得到去噪后的SAR图像。但经验模态分解后的高频IMF中仍含有一定的细节信息,低频IMF中也含有部分噪声,因此部分重构方法又限制了EMD相干斑抑制性能的进一步提高。
为了取得更好的相干斑抑制效果,王文波等[12]将EMD与主成分分析(principal component analysis, PCA)方法相结合,利用PCA去除各层IMF中的噪声。但PCA是一种线性数据处理方法,往往不能检测出给定数据中的所有结构,特别是一些非线性结构;而核主成分分析(kernel principal component analysis, KPCA) 非常适合于处理非线性问题,与PCA相比能提取出SAR图像中更多的有用信息[13-14]。因此,为了改善对SAR图像中非线性地物结构的检测性能,进一步提高相干斑抑制效果,本文将KPCA引入到SAR图像去噪中,提出一种基于EMD和KPCA的SAR图像相干斑抑制算法,并通过图像去噪实验进行算法验证。
1核主成分分析
KPCA的基本思路是:首先通过一个非线性函数Φ把数据yk∈RN(k=1,…,L)映射到一个高维的特征空间F,然后对映射后的数据进行线性PCA变换。
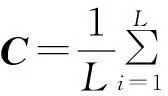

(1)

通过以上分析可知,基于KPCA的图像去噪方法可归纳为:对含噪图像信号x,通过非线性变换Φ映射到特征空间F,在F中仅保留包含大量信息的主成分,丢弃只含少量信息的噪声成分项而得到PnΦ(x),再由PnΦ(x)计算出原始图像x的重建图像z,从而达到去噪的目的。
2基于KPCA的EMD相干斑抑制算法
在利用KPCA对SAR图像各层IMF去噪时,一个很重要的问题是如何选择合适的主成分予以保留。如果保留的主成分过多,会导致噪声不能被有效去除;如果保留的主成分过少,又会损失较多的细节信息;而且每层IMF中所含噪声的强度不同,在对不同层IMF进行处理时选择予以保留的主成分的标准不相同。因此下面将重点讨论如何根据IMF中噪声能量占总能量的比例自适应选择应保留的主成分数目。
2.1对数SAR图像IMF的能量构成模型
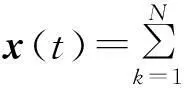
本文利用EMD对SAR图像去噪时,首先对其进行对数变换和均值调整,使相干斑噪声近似变为加性零均值高斯白噪声[15]。设均值调整后的对数SAR图像为I(i,j)(1≤i≤p,1≤j≤q),为了方便,将I(i,j)记为I(n)(1≤n≤p·q)。设I(n)经EMD分解后,第k层本征模态函数记为fk=[d1,d2,…,dM],fk的能量ε(fk)定义为
(2)
式中:M为fk的长度。设
(3)
式中:gk为fk中所包含的信号成分;Wk为fk中所包含的噪声成分。则有
(4)
式中:E(·)表示期望。

(5)
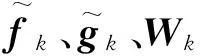
因为信号gk与噪声Wk无关,所以
(6)
因此
(7)
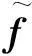

对数SAR图像经EMD分解后,第k层IMF的能量为ε(fk),其所含噪声的能量为ε(Wk)。由文献[16]可知,ε(Wk)和ε(W1)之间的关系近似满足
(8)
式中:β≈0.719,ρ≈2.01。因此,如果能求出含噪信号第一层IMF中所含噪声的能量ε(W1),则可通过式(8)求出第k层IMF中所含噪声的能量ε(Wk)。
2.3主成分的选择方法
假设待去噪数据为
(9)
式中:y为不含噪声的信号数据;W为与y无关的零均值高斯白噪声。设KPCA去噪过程中训练数据集为xk∈RN,k=1,…,L,且其在特征空间F的映射{Φ(xk)}为零均值;所用核函数为k(x,y),核变换矩阵K=(Kij)=(Φ(xi)·Φ(xj))=k(xi,xj)的特征值为λ1≥λ2≥…≥λL,相应的特征向量分别为α1,α2,…,αL。
(10)
根据式(6)与式(7),通过相同推导可知
(11)

为了方便计算并减小误差,将式(11)变化为:
(12)

(13)

(14)
如果存在η使得
(15)
则令H=η。
2.4算法步骤
(1) 计算SAR图像I(i1,i2)的边缘方向[8],取核函数k(x,y)=[a(x·y)]d。
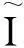
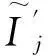
3算法检验与结果分析
为了客观评价斑点噪声的去除效果,本文从以下三个方面进行分析[15-16]:
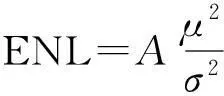
(2)均值比(MR)反映相干斑抑制算法对图像辐射特性的保持程度。均值比越接近1,表明抑斑图像辐射特性保持得越好。
(3)标准差(STD)反映图像的像素灰度值与灰度均值之间的分散程度。通过相干斑抑制后,斑点噪声强度减弱,图像的标准差将会减小。
选用两幅SAR图像进行相干斑抑制实验:①像素大小为512×512、分辨率为1m、等效视数为2的X波段幅度SAR图像1;②像素大小为512×512、分辨率为1m、等效视数为3的Ku波段幅度SAR图像2。
分别采用本文算法(EMD-KPCA)、EMD模态单元阈值去噪算法(EMD-CIIT)[17]和EMD主成分分析去噪算法(EMD-PCA)[12]对两幅SAR图像进行处理。在EMD-CIIT中,采用文献[8]中的方法根据边缘信息选取相应的去噪结果。在EMD-PCA和本文方法中,核函数参数a=2、d=3。采用循环迭代的方法计算式(15)中参数θ的最优取值(θ从0.9到1.0按步长0.01取值),本文中θ取值为0.94。SAR图像1和图像2的相干斑抑制实验结果分别如图1和图2所示,从图中可以看出,采用本文方法去噪后的图像具有更好的视觉效果。

(a) 原始图像

(b)EMD-CIIT去噪

(c) EMD-PCA去噪

(d)EMD-KPCA去噪

(a) 原始图像

(b)EMD-CIIT去噪

(c) EMD-PCA去噪

(d)EMD-KPCA去噪
为了进一步比较各个算法的相干斑抑制效果,在两幅测试图像中分别选择3个矩形区域(见图1(a)和图2(a)),计算各区域内的等效视数ENL,而均值比和标准差则是对整幅SAR图像进行计算得到的。评价指标计算结果如表1和表2所示。
表1SAR图像1采用不同去噪方法的相干斑抑制性能指标对比
Table 1 Comparison of speckle suppression performance indexes of SAR Image 1 denoised by different methods

ENL区域1区域2区域3MRSTD原始图像2.832.063.14—33.59EMD-CIIT去噪9.318.7510.671.194517.48EMD-PCA去噪19.6217.2128.751.097714.22EMD-KPCA去噪22.3121.8332.591.016410.11
表2SAR图像2采用不同去噪方法的相干斑抑制性能指标对比
Table 2 Comparison of speckle suppression performance indexes of SAR Image 2 denoised by different methods
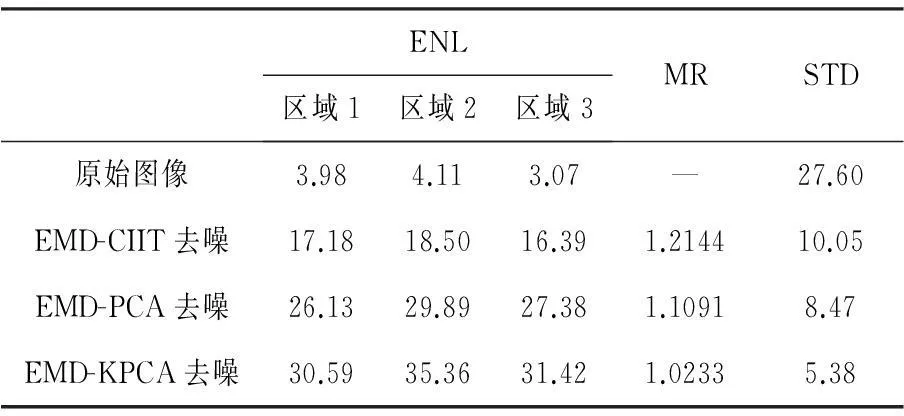
ENL区域1区域2区域3MRSTD原始图像3.984.113.07—27.60EMD-CIIT去噪17.1818.5016.391.214410.05EMD-PCA去噪26.1329.8927.381.10918.47EMD-KPCA去噪30.5935.3631.421.02335.38
从表1和表2可以看出,三种方法去噪后图像的等效视数ENL都有较大的提高,表明这些方法对相干斑噪声都有较好的抑制效果。但本文方法在三个区域内的等效视数都要高于另外两个方法的对应值。而且EMD-KPCA去噪图像的均值比MR最接近于1,这表明采用本文方法去噪后SAR图像的辐射特性保持得最好。另外,去噪图像的标准差STD都比原图像大幅降低,表明这三种方法都具有较强的噪声滤除能力,其中本文方法去噪后的图像STD值最小。综上所述,与EMD-CIIT和EMD-PCA方法相比,不论是从主观视觉效果来看,还是从定量的客观评价指标来看,本文方法都具有优势。
4结语
本文在传统EMD部分重构算法的基础上,结合KPCA提出了一种改进的EMD相干斑点抑制算法。首先计算SAR图像经EMD分解后各层IMF中所含噪声的能量;然后再利用KPCA对IMF进行分解,即根据各层IMF中噪声能量占IMF总能量的比例删除一定量的主成分,使得所删除主成分的能量与IMF中噪声能量近似相同;最后对经KPCA处理后的各层本征模态函数 进行累加重构,完成对SAR图像的去噪。两组SAR图像去噪实验结果表明,与基于阈值的EMD去噪算法和基于PCA的EMD去噪算法相比,本文方法在相干斑抑制效果和细节信息保持能力两方面都有较好的提高。
参考文献
[1]Fabruzui A, Tiziano B, Luciano A. Multiresolution MAP despeckling of SAR images based on locally adaptive generalized Gaussian pdf modeling[J]. IEEE Transactions on Image Processing, 2006, 15(11): 3385-3399.
[2]Maryam Amirmazlaghani, Hamidreza Amindavar, Alireza Moghaddamjoo. Speckle suppression in SAR images using the 2-D GARCH model[J]. IEEE Transactions on Image Processing, 2009, 18(2):250-259.
[3]Foucher S, Bénié G B, Boucher J-M. Multiscale MAP filtering of SAR images[J]. IEEE Transactions on Image Processing, 2001,10(1):49-60.
[4]Solbø S, Eltoft T. A stationary wavelet-domain Wiener filter for correlated speckle[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(4):1219-1230.
[5]Dai M, Peng C, Chan A K, et al. Bayesian wavelet shrinkage with edge detection for SAR image despeckling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(8): 1642-1648.
[6]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A Mathematical Physical and Engineering Sciences, 1998, A454:903-995.
[7]Huang N E, Shen Z , Long S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review and Fluid Mechanics, 1999, 31: 417-457.
[8]Han Chunming, Guo Huadong, Wang Changlin, et al. A novel method to reduce speckle in SAR images[J]. International Journal of Remote Sensing, 2002, 23(23):5095-5101.
[9]韩春明, 郭华东, 王长林. 利用经验模态分解方法抑制SAR斑点噪声[J]. 遥感学报, 2002, 6(4):266-271.
[10]Yue Huanyin, Guo Huadong, Han Chuming, et al. A SAR interferogram filter based on the empirical mode decomposition method[C]//IEEE 2001 International Geoscience and Remote Sensing Symposium. Sydney, July 9-13, 2001, 5:2061-2063.
[11]Zhou Feng, Xing Mengdao, Bai Xueru, et al. Narrow-band interference suppression for SAR based on complex empirical mode decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 423-427.
[12]王文波, 赵攀, 张晓东. 利用经验模态分解和主成分分析的SAR图像相干斑抑制[J]. 测绘学报, 2012,41(6):838-843.
[13]Teixeira A R, Tomé A M, Stadlthanner K, et al. KPCA denoising and the pre-image problem revisited[J]. Digital Signal Processing, 2008, 18(4):568-580.
[14]Kwok J T, Tsang I W. The pre-image problem in kernel methods[J]. IEEE Transactions on Neural Networks, 2004, 15(6):1517-1525.
[15]Xie H, Pierce L E, Ulaby F T. SAR speckle reduction using wavelet denoising and Markov random field modeling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(10):2196-2212.
[16]常霞, 焦李成, 刘芳,等. 基于斑点方差估计的非下采样Contourlet域SAR图像去噪[J]. 电子学报, 2010, 38(6):1328-1333.
[17]Kopsinis Y, McLaughlin S. Development of EMD-based denoising methods inspired by wavelet thresholding[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1351-1362.
[责任编辑尚晶]
SAR image despeckling based on empirical mode decomposition andkernel principle component analysis
LiChangchao1,2,WangWenbo3
(1. College of Computer Science and Technology, Wuhan University of Science and Technology,Wuhan 430065, China;2. Hubei Province Key Laboratory of Intelligent Information Processing and Real-time Industrial System,Wuhan University of Science and Technology, Wuhan 430065, China;3. College of Science,Wuhan University of Science and Technology,Wuhan 430065,China)
Abstract:This paper proposes a speckle suppression method for SAR image using empirical mode decomposition (EMD) and kernel principle component analysis (KPCA). Firstly,SAR image after logarithmic transformation and mean adjustment is decomposed by EMD. Then the noises in the intrinsic mode functions (IMF) are removed by KPCA, which is performed as follows: the proportion of noise energy in each IMF is approximately calculated based on the statistical properties of speckle noise and IMF energy distribution model of Gaussian white noise with zero mean, and IMF is reconstructed by selecting the appropriate principle components according to the noise energy proportion. Finally, the denoised SAR image is obtained by accumulating the intrinsic mode functions processed by KPCA. Experimental results show that, compared with two other EMD-based image denoising algorithms, the proposed method has better performance in suppressing speckle noise and preserving detail image information.
Key words:SAR image; speckle suppression; EMD; KPCA; IMF; image denoising
收稿日期:2016-04-09
基金项目:国家自然科学基金资助项目(11201354);卫星海洋环境动力学国家重点实验室资助项目(SOED1405).
作者简介:李长超(1983-),男,武汉科技大学教师. E-mail:19404425@qq.com
中图分类号:TP751
文献标志码:A
文章编号:1674-3644(2016)03-0224-07

