求解非线性P0互补问题的填充函数法
袁柳洋,唐秋华,贾世会
(1.武汉科技大学理学院,湖北 武汉,430065;2.武汉科技大学机械自动化学院,湖北 武汉,430081 )
求解非线性P0互补问题的填充函数法
袁柳洋1,唐秋华2,贾世会1
(1.武汉科技大学理学院,湖北 武汉,430065;2.武汉科技大学机械自动化学院,湖北 武汉,430081 )
摘要:首先利用光滑Fischer-Burmeister函数, 将非线性P0互补问题转化成相应的约束优化问题;然后对此约束优化问题构造出一种新的无参数的填充函数, 讨论了该填充函数的有关性质,并提出了求解非线性P0互补问题的填充函数算法。通过几个数值算例验证了该算法的有效性。
关键词:非线性互补问题;P0函数;Fischer-Burmeister函数;填充函数; 局部极小点;全局极小点
1问题描述
本文考虑如下形式的非线性互补问题(简写为NCP(F)):找到一个向量x*∈Rn, 满足
(1)
式中:F(x)∶Rn→Rn是一个非线性向量函数。若F(x)=Mx+q, 其中M∈Rn×n,q∈Rn, 则NCP(F)被称为线性互补问题, 简写为LCP(M,q)。若F是P0函数,即对任意的u,v∈Rn,u≠v, 存在下标k(1≤k≤n), 使得
(2)
同时成立, 则称NCP(F)为非线性P0互补问题。
非线性P0互补问题是单调互补问题和P函数互补问题的推广, 近年来受到许多学者的关注。求解非线性P0互补问题最常用的方法是牛顿法[1-2]、磨光算法[3]等, 而本文将提出另外一种求解方法——填充函数法。
在大多数求解非线性P0互补问题的算法中, 最普遍的做法是先通过NCP函数将非线性P0互补问题转化成一个方程组, 然后再用求解方程组的方法间接求解。本文则首先利用NCP函数中的光滑Fischer-Burmeister函数, 将非线性P0互补问题转化成相应的约束优化问题,然后根据填充函数的定义, 对此约束最优化问题构造出一种新的无参数的填充函数, 并分析讨论该填充函数的有关性质,最后建立求解非线性P0互补问题的填充函数算法。
2非线性P0互补问题的转化
minθ(x)

(3)
并且θ()=0。

(4)
式中:x=(x1,…,xn)T;F(x)=(F1(x),…,Fn(x))T。

(5)
否则, θ定义为
(6)
NCP函数有很多种, 其中非常重要的一种是Fischer-Burmeister函数:
(7)

(8)

令
(9)
并定义
(10)
显然H(z)=0⟺μ=0,x是NCP(F)的解。
上述方程组又可转化为如下的约束优化问题:
minf(z)=‖H(z)‖2

(11)
式中:‖·‖2为欧几里得范数;X={(μ,x)|μ>0,x∈Rn}。
若x*是NCP(F)的一个解, 当且仅当z*是问题(11)的全局最优解且最优值f(z*)=0。
3填充函数的构造及其性质分析
考虑问题(11), 在本文中做如下假设。
假设2NCP(F)的解集非空且有界。
下面给出填充函数的定义。
定义3[4]函数P(z,z*)被称为f(z)在局部极小点z*处的填充函数, 如果它满足:
(1)z*是P(z,z*)的一个严格局部极大点;
(2)对任意的z∈S1, 有P(z,z*)≠0, 其中S1={z|f(z)≥f(z*),z∈X{z*}};

不少研究人员[4-11]提出的填充函数都具有一个或两个参数, 而在实际计算中, 这些填充函数参数必须满足一些条件才能符合其定义,而这将大大增加计算量。文献[5]中指出, 要克服其所提出的填充函数的缺陷,有一种方法是构造单参数或无参数的填充函数。本文据此提出了一种新的无参数的填充函数:
(12)
式中:z*是问题(11)的当前局部极小点;对r>0,hr(t)定义为
(13)

以下的定理表明F(z,z*)满足填充函数的定义3。
定理1若z*∈X满足f(z*)>0, 则z*是F(z,z*)的严格极大点。
证明:由于当t∈R时, 0≤hr(t)≤1, 则由F(z,z*)的定义, 可得
因此,z*是F(z,z*)的严格极大点。
定理1表明F(z,z*)满足定义3的条件(1)。
定理2若z*∈X满足f(z*)>0, 则对任意的z∈S1={z|f(z)≥f(z*),z∈X{z*}} , 有F(z,z*)≠0。
因此,对任意的z∈S1, 有F(z,z*)≠0。
定理2表明F(z,z*) 满足定义3的条件(2)。


定理3表明F(z,z*)满足定义3的条件(3)。
4算法描述

考虑如下的填充函数问题:
(14)
本文算法简称为APPF,具体步骤如下。
步骤0选择足够小的正数λL;选择一个正整数K和方向ei,i=1,…,K;选择一个初始点z0∈X;置k∶=0。

步骤2令
其中,
置l∶=1和λ∶=1。
步骤3
(a) 若l≤K, 转(b); 否则, 转步骤5。


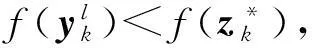

(15)


APPF算法的主要思想是:
(1)按以下方法选取步骤0中的方向ei。例如,当n=2时, 取K=6n,方向ei被选为
当n≥3时, 取K=2n,这时,当i=1,…,n时,ei中的第i个分量为1, 其他分量为0;当i=n+1,…,K时,ei中的第i个分量为-1, 其他分量为0。


5算法验证

例1NCP(F)中的函数F由下式给出:
该函数是P0函数, 它有唯一的解(2,0,1,0)T, 取μ的初值μ0=0.1。
例1的数值计算结果见表1。由表1可知, 两种算法的计算结果相同, 但本文APPF算法所需要的CPU时间更短。

表1 例1的数值计算结果
注:t为找到第k个局部极小点时所需要的CPU时间。
例2NCP(F)中的函数F由下式给出:
例2的数值计算结果见表2。同样,APPF算法与AOPF算法的计算结果相同, 但前者所花CPU时间更少。
由以上算例可推知, 采用APPF算法和AOPF算法可得到相同的数值结果, 但大多数情况下前者的计算效率更高。这是因为,一般来说判断目前的点是全局极小点比找到全局极小点更花时间。

表2 例2的数值计算结果
注:t为找到第k个局部极小点时所需要的CPU时间。
6结语
本文首先通过光滑的Fischer-Burmeister函数, 将非线性P0互补问题转化为相应的约束优化问题(11)。然后根据填充函数的定义, 对问题(11) 构造出了一种无参数的填充函数F(z,z*),分析讨论了该填充函数的有关性质。最后构造了求解非线性P0互补问题的填充函数算法, 并对该算法进行了数值实验。针对所给的两个算例,本文APPF算法和文献[6]中AOPF算法虽有同样的数值结果,但APPF算法所使用的CPU时间更少,因此该填充函数算法是有效的。
参考文献
[1]Huang N, Ma C F. The numerical study of a regularized smoothing Newton method for solvingP0-NCP based on the generalized smoothing Fischer-Burmeister function[J].Applied Mathematics and Computation, 2012, 218: 7253-7269.
[2]Zhang L P, Wu S -Y, Gao T R. Improved smoothing Newton methods forP0nonlinear complementarity problems[J]. Applied Mathematics and Computation, 2009, 215: 324-332.
[3]Zhu J G, Liu H W, Li X L. A regularized smoothing-type algorithm for solving a system of inequalities with aP0-function[J]. Journal of Computational and Applied Mathematics, 2010, 233:2611-2619.
[4]Yang Y J, Shang Y L. A new filled function method for unconstrained global optimization[J]. Applied Mathematics and Computation, 2006, 173: 501-512.
[5]Ge R P. A filled function method for finding a global minimizer of a function of several variables[J]. Mathematical Programming, 1990, 46: 191-204.
[6]Yuan L Y, Wan Z P, Zhang J J, et al. A filled function method for solving nonlinear complementarity problem[J]. Journal of Industrial and Management Optimization, 2009, 5(4): 911-928.
[7]Zhang L S, Ng C-K, Li D, et al. A new filled function method for global optimization[J]. Journal of Global Optimization, 2004, 28:17-43.
[8]Xu Z, Huang H-X, Pardalos P M, et al. Filled functions for unconstrained global optimization[J]. Journal of Global Optimization, 2001, 20:49-65.
[9]Liu H W, Gao Y L,Wang Y P. A continuously differentiable filled function method for global optimization[J]. Numerical Algorithms, 2014, 66: 511-523.
[10]Wei F, Wang Y P,Lin H W. A new filled function method with two parameters for global optimization[J]. Journal of Optimization Theory and Applications, 2014, 163: 510-527.
[11]Yuan L Y, Wan Z P, Tang Q H. A criterion for an approximation global optimal solution based on the filled functions[J]. Journal of Industrial and Management Optimization, 2016, 12(1): 375-387.
[责任编辑尚晶]
A filled function method for nonlinearP0complementarity problems
YuanLiuyang1,TangQiuhua2,JiaShihui1
(1.College of Science, Wuhan University of Science and Technology, Wuhan 430065, China;2. College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China)
Abstract:Firstly, the nonlinear P0 complementarity problem is converted into a corresponding constrained optimization problem by using the smoothing Fischer-Burmeister function. Subsequently, a novel parameter-free filled function is constructed for the constrained optimization problem,and the function’s properties are also discussed. A filled function algorithm is proposed to solve the nonlinear P0 complementarity problem, and its validity is verified by several numerical examples.
Key words:nonlinear complementarity problem; P0 function; Fischer-Burmeister function; filled function; local minimizer; global minimizer
收稿日期:2016-01-21
基金项目:国家自然科学基金青年科学基金项目(11401450,11401126);国家自然科学基金面上项目(51275366).
作者简介:袁柳洋(1988-),女,武汉科技大学讲师,博士. E-mail:yangly0601@126.com通讯作者:唐秋华(1971-),女,武汉科技大学教授,博士生导师. E-mail:tangqiuhua@wust.edu.cn
中图分类号:O224
文献标志码:A
文章编号:1674-3644(2016)03-0236-05

