地震作用下顺层岩质边坡动力可靠度

李　逸，　龚文惠，　陈训龙，　邱金伟，　钟旭晗

(华中科技大学　土木工程与力学学院, 湖北　武汉　430074)



地震作用下顺层岩质边坡动力可靠度

李逸，龚文惠，陈训龙，邱金伟，钟旭晗

(华中科技大学土木工程与力学学院, 湖北武汉430074)

摘要：针对地震的动力特性以及岩体强度参数的随机性，提出计算地震作用下顺层岩质边坡动力可靠度时程的方法，并提出以最小平均安全系数和平均大失效概率作为联合评价指标来评价顺层边坡的整体稳定性。首先，建立了顺层岩质边坡地震响应的分析模型，根据得到的岩体应力地震响应求出了顺层岩质边坡的动力安全系数时程曲线；建立了顺层岩质边坡极限状态方程，并运用JC法求出了边坡的失效概率时程曲线。最后，求出了顺层岩质边坡的最小平均安全系数和平均大失效概率。算例分析表明，与传统方法相比，采用最小平均安全系数和平均大失效概率来作为评价顺层岩质边坡稳定性的综合指标，能更安全地评价边坡的稳定性。

关键词：顺层岩质边坡；地震作用；动力可靠度；JC法

近年来，因地震作用而诱发的顺层边坡滑坡越来越频繁，地震作用下的顺层边坡稳定性研究具有十分重要的理论和实际意义。

目前，地震作用下顺层边坡稳定性研究[1～3]大多是基于确定性分析方法，主要有拟静力法、Newmark分析法、动力有限元时程分析法。拟静力法是规范规定的工程上常用的方法，该方法是在静力荷载下采用静力的方法求得，Newmark分析法[4]国外应用较多，是通过对超过滑移体屈服加速度的那部分加速度进行两次时间积分来计算出边坡的地震累积滑移量，并以此作为边坡稳定性的评价指标。动力有限元时程分析法将每一时刻的动应力施加到静应力上，然后按静力方法计算得到每一时刻的安全系数，最后得到安全系数时程曲线。然而，以上方法均未考虑顺层岩质边坡稳定性影响因素的不确定性。

影响顺层岩质边坡稳定性的参数[5,6]具有很大的随机性，单凭某一特定状态下的参数求得安全系数并不能全面反映地震作用下的顺层岩质边坡安全状态。因此，近年来国内外学者尝试运用结构可靠度分析方法来分析顺层边坡稳定性，计算出顺层边坡可靠度。高荣雄等[7]采用摄动随机有限元法进行了顺层边坡稳定性和可靠度的分析；曾胜等[8]分析了红砂岩顺层岩质边坡稳定性；陈昌富等[9]对顺层岩质边坡可靠度的求解方法进行了优化。目前，对于地震作用下顺层岩质边坡可靠性分析的研究还比较少，并且这些研究在顺层边坡地震应力反应分析过程中，采用拟静力法来处理地震作用，无法体现地震的动力特性。如Low等[10]基于拟静力法和改进的一次二阶矩法对地震作用下顺层岩质边坡的可靠性进行了分析。

此外，对于动力法分析得到的动力安全系数时程曲线，目前尚无一个明确的标准来判断边坡是否失稳。张建海等提出用边坡的最小动力安全系数作为稳定性评价指标[11]；刘汉龙等提出用最小平均安全系数来作为评价指标[12]；薄景山等提出用平均安全系数来作为稳定性评价指标[13]。这些分析方法都限于确定性分析，即往往只是考虑单一条件下的安全系数来作为边坡稳定评价指标。

基于此，本文以顺层边坡为研究对象，考虑地震的动力特性以及岩体强度参数的不确定性，分析顺层岩质边坡的动力可靠度和失效概率时程曲线。提出以边坡的最小平均安全系数[12]和平均大失效概率作为联合评价指标的边坡稳定性评价方法。

1地震作用下应力分析

进行地震作用下应力分析时，假设顺层岩质边坡沿通过坡脚的软弱结构面发生平面滑动破坏，如图1所示(α为顺层边坡滑动面的倾角)。破坏准则为Mohr-Coulomb准则。

图1　顺层边坡破坏模式

1.1边坡应力分析

应用静力有限元法计算边坡在地震前的初始应力状态，目的是为边坡动力稳定分析提供初始应力状态。求解公式如下：

[K]{u}={p}

(1)

式中：[K]为结构整体刚度矩阵；{u}为结构位移矩阵；{p}为结构外荷载矩阵。

根据各节点的位移值计算相应的应变值，从而求得单元的静应力分量σxs,σys,τxys。σxs表示单元x方向的静正应力分量；σys表示单元y方向的静正应力分量；τxys表示单元静剪应力分量。

地震作用下，结构运动方程为：

(2)

结构整体阻尼矩阵[C]由各单元阻尼矩阵组成，单元阻尼矩阵采用Rayleigh阻尼：

[C]e=α0[M]e+α1[K]e

(3)

(4)

式中：[M]e为单元质量矩阵；[K]e为单元刚度矩阵；ξ为阻尼比率；ωi、ωj为结构的自振圆频率。

对动力方程(1)采用时域逐步积分法求解，可以得到每一时刻所有单元的动应力分量σxd,σyd,τxyd。σxd表示单元x方向的动应力分量，σyd表示单元y方向的动正应力分量，τxyd表示单元的动剪应力分量。

1.2滑动面单元应力求解

滑动面上单元的应力求解在边坡静力分析和动力分析的基础上进行。滑动面示意图如图2。

图2　滑动面示意

上图中，取滑动面上一个单元进行分析。由静力计算式(1)可得滑动面单元x，y方向静正应力与静剪应力σxsi，σysi，τxysi。由动力计算式(2)～(4)可得滑动面单元x，y方向动正应力和动剪应力σxdi，σydi，τxydi。再由式(5)～(8)得单元静正应力、静剪应力、动正应力与动剪应力σnsi，τsi，σndi，τdi。因此，滑动面上的正应力σi=σnsi+σdi，滑动面上的剪应力τi=τnsi+τdi。

(5)

(6)

(7)

(8)

2顺层岩质边坡动力可靠度分析

2.1边坡动力极限状态方程

计算出滑动面单元上的正应力与剪应力后，可以计算边坡各个时刻的动力安全系数

(9)

式中:c表示岩土体粘聚力;li表示第i个单元滑动面长度;φ表示岩土体内摩擦角;Ni=σi·li，Ti=τi·li，σi表示第i个单元滑动面上的正应力，τi表示第i个单元滑动面上的剪应力。

通过计算地震作用下边坡各个时刻的安全系数，可以得到边坡的动力安全系数时程曲线。

实际上，岩土体的内聚力和内摩擦角的具体数值是未知的，因此可以当作随机变量来考虑。边坡的极限状态方程为：

(10)

2.2边坡动力可靠度求解

根据文献[13]，假定岩土体的内摩擦角φ服从正态分布，粘聚力c服从对数正态分布。采用验算点法来计算结构可靠指标β时，由于基本变量Z中含有非正态随机变量c，因此先要处理非正态随机变量。采用当量正态法即JC法处理非正态随机变量c。

假设随机变量c的均值为μc，标准差为σc，概率密度函数为fc(c)，累计分布函数为Fc(c)；与C相应的当量正态化标量为C′，相应的均值为μc′，标准差为σc′，相应的概率密度函数为fc′(c′)，累积分布函数为Fc′(c′)。JC法的当量正态化条件要求在验算点c*处C′和C的累计分布函数和概率密度函数分别相等，即：

(11)

(12)

根据当量正态化条件，可以得到当量正态化变量的均值和标准差。对式(13)和(14)求反函数得到：

μc′=c*-Φ-1[FC(c*)]σc′

(13)

(14)

在数值计算中，并不需要针对随机变量c的具体分布推导出其当量正态化随机变量c′的均值和标准差的显示表达式。

将随机变量c当量正态化后，即可以参照独立正态分布变量的验算点法迭代步骤，建立JC法的迭代计算步骤，从而计算出结构的可靠指标β。

边坡的可靠指标β与边坡失效概率pf的关系为：

pf=1-Φ(β)

(15)

计算出顺层岩质边坡在地震作用下各个时刻的失效概率，可以得到地震作用下顺层岩质边坡的失效概率时程曲线。

3顺层岩质边坡稳定评价指标

虽然边坡动力安全系数时程和动力可靠度时程能够很好地考虑地震动的特性及边坡岩土体的特性，反映了边坡安全系数和动力可靠度随时间的动态变化过程。但是通过安全系数时程和动力可靠度时程，只能了解边坡在地震动作用下动力稳定性的变化范围，无法评价边坡整体等效稳定性和确定边坡抗震加固标准。本文在评价边坡整体稳定性时，综合考虑最小平均安全系数和平均大失效概率。

3.1边坡最小平均安全系数

根据文献[7]，边坡最小平均安全系数

(16)

式中：Ks0为边坡在静力作用下的稳定安全系数；Ksmin为动力荷载作用下的各个时刻的动力安全系数Ks的最小值。

3.2边坡平均大失效概率

在评价地震作用下岩质边坡整体稳定性时，用平均失效概率来作为评价指标是不够安全的。在地震作用下，边坡失效概率应大于静力作用下的边坡失效概率。因此，本文定义平均大失效概率来评价地震作用下顺层岩质边坡的整体稳定性，平均大失效概率计算式为：

(17)

图3　平均大失效概率计算示意

为方便计算，取

(18)

式中：pff为失效概率时程曲线大于pf0的每一步长时刻的值，称为大失效概率；n为时程曲线上大失效概率的个数。

根据文献[14]，边坡的安全等级可由表1确定。

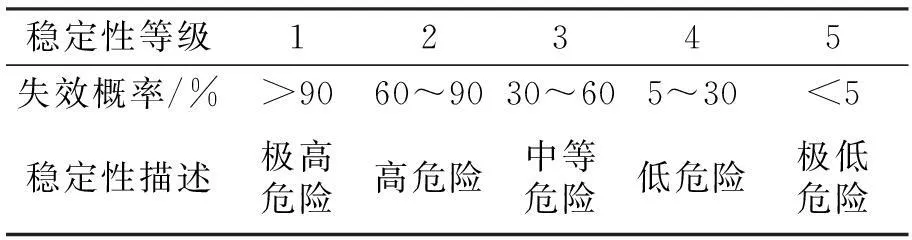
表1　边坡稳定性分类等级

在评价边坡稳定性时，可以综合考虑最小平均安全系数和平均大失效概率。

4算例分析

4.1工程概况

以沪蓉国道主干线宜昌至恩施公路某一段顺层岩质路堑边坡为例进行分析，坡高H=23 m，坡角45°，结构面倾角35°。边坡的几何尺寸如图4所示，岩体物理力学参数由室内外试验获得，具体参数见表2，其中内摩擦角服从正态分布，粘聚力服从对数正态分布。

图4　边坡结构几何尺寸示意/m

岩层密度/(kg/m3)剪切模量/GPa体积模量/GPa内摩擦角/(°)平均值标准差粘聚力/kPa平均值标准差抗拉强度/kPa结构面23001.653.04325.01304.3110岩体260010.7114.62477.231000132.391600

图5　边坡网格划分示意

静力计算时，模型底部采用固定边界条件，模型两边固定住x方向的位移。在动力计算时，模型底部采用静态边界条件，模型四周采用自由场边界条件。

输入的地震荷载采用处理后的Landers地震波数据，持续时间为20 s。输入地震的加速度时程如图6所示。地震波采用在边坡底部用加速度时程方式输入方向为x方向的地震波。

图6　地震加速度时程曲线

4.2计算结果及分析

计算动应力时，为了得到动力安全系数和动力可靠度时程曲线，每0.5 s计算一次应力情况。通过有限差分软件静力计算得到各个单元在重力作用下的静应力，然后计算出各个单元在地震荷载作用下的动应力，单元的应力等于静应力与动应力相加。利用公式(5)～(8)计算出结构面各单元的正应力与剪应力。

(1)边坡最小平均安全系数

利用式(9)求解出结构各个时刻的动力安全系数，绘出动力安全系数时程曲线如图7所示。

图7　边坡安全系数时程曲线

(2)边坡平均大失效概率

由式(10)～(15)，可求出边坡各个时刻的失效概率，失效概率时程曲线如图8所示。

图8　边坡失效概率时程曲线

最后在评价顺层岩质边坡整体稳定性时，综合考虑边坡的最小平均安全系数和平均大失效概率，可知本文边坡模型是处于低危险状态的。

4.3对比分析

与传统方法进行比较，比较结果见表3，其中传统方法为采用拟静力法和JC法求解安全系数和可靠度。

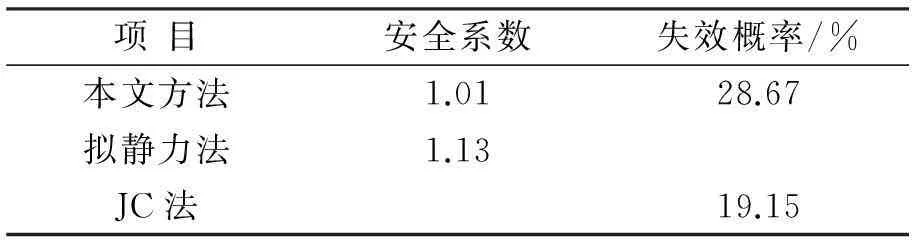
表3　结果对比

由表3可知，与传统方法相比，本文计算出的最小平均安全系数偏低，平均大失效概率偏高，说明本文在计算过程中充分考虑了顺层岩质边坡的动力特性，较传统方法更加安全。

5结论

本文结合工程，开展了地震作用下顺层岩质边坡的动力可靠度分析方法探讨，计算出了边坡最小平均安全系数和平均大失效概率。得出如下结论：

(1)由于考虑了地震的动力特性和边坡强度参数的随机性，本文求得的顺层岩质边坡最小平均安全系数较传统方法的计算结果偏低，平均大失效概率较传统方法偏高，因而使评价结果更全面和符合实际。

(2)本文采用最小平均安全系数和平均大失效概率作为联合评价指标来评价地震作用下边坡的稳定性，能较好地显示边坡在地震过程中的真实状态和总体稳定状态。

参考文献

[1]郝建斌. 地震作用下边坡稳定性研究进展[J]. 世界地震工程, 2014, 30(1): 145-153.

[2]郑颖人, 叶海林, 黄润秋, 等. 边坡地震稳定性分析探讨[J]. 地震工程与工程振动, 2010, 30(2): 173-180

[3]叶海林, 黄润秋, 郑颖人, 等. 地震作用下边坡稳定性安全评价的研究[J]. 地下空间与工程学报, 2009, 5(6): 1248-1252.

[4]李明, 辛鸿博, 孙丽敏. Newmark滑块分析法评价土质边坡地震稳定性的研究进展[J]. 工业建筑, 2014, (s1): 722-726.

[5]龚文惠, 王平, 陈峰. 顺层岩质路堑边坡稳定性的敏感性因素分析[J]. 岩土力学, 2007, 28(4): 812-816.

[6]冯君, 吕和林, 李安洪. 顺层岩质边坡稳定性影响因素分析[J]. 四川建筑科学研究, 2005, 31(4): 78-80.

[7]高荣雄, 龚文惠, 王元汉, 等. 顺层岩质边坡稳定性及可靠度的随机有限元分析法[J]. 岩土力学, 2009, 30(4): 1165-1169.

[8]曾胜, 李振存, 韦慧, 等. 降雨渗流及干湿循环作用下红砂岩顺层岩质边坡稳定性分析[J]. 岩土力学, 2013, 34(6): 1536-1540.

[9]陈昌富, 朱朝银, 刘跃鹏. 顺层岩质边坡可靠度优化分析及其应用[J]. 新疆有色金属, 1996，(4): 6-10.

[10]Low B K. Reliability analysis of rock slopes involving correlated nonnormals[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 922-935.

[11]张建海, 范景伟, 何江达. 用刚体弹簧元法求解边坡、坝基动力安全系数[J]. 岩石力学与工程学报, 1999, 18(4): 19-23.

[12]刘汉龙, 费康, 高玉峰. 边坡地震稳定性时程分析方法[J]. 岩土力学, 2003, 24(4): 553-556.

[13]常晓林, 黄东军, 蒋春艳, 等. 重力坝抗滑稳定设计表达式及分项系数研究[J]. 岩土工程学报, 2007, 29(8):1219-1223.

[14]陈坤杰. 基于可靠度理论的风化岩质边坡稳定性分析研究[D]. 长沙: 长沙理工大学, 2013.

Dynamic Reliability Analysis on Rock Slopes Under Earthquake

LIYi,GONGWen-hui,CHENXun-long,QIUJin-wei,ZHONGXu-han

(School of Civil Engineering and Mechanics, Huazhong University of Science and Technology,Wuhan 430074, China)

Abstract:For the dynamic characteristics of the earthquake and the randomness of rock’s strength parameters, a new method is put forward to calculate the time-history of dynamic reliability of bedrock slope under earthquake. The minimum average safety factor and the average big failure probability are considered as the combined evaluation index to evaluate the overall stability of bedrock slope. First, analytical model is established to analyse the seismic response of bedrock slope and the time-history curve of dynamic safety is solved according to the earthquake response of the rock slope, the limit state functions of bedrock slope is established and the time-history curve of the failure probability is solved with JC method. Finally, the minimum average safety factor and the average big failure probability is solved. The numerical example shows that, compared with traditional methods, we can evaluate the overall stability of bedrock slope more safely when the minimum average safety factor and the average big failure probability are considered as the combined evaluation index to evaluate the overall stability of bedrock slope.

Key words：bedding rock slope; earthquake; dynamic reliability; JC method

收稿日期：2015-11-06修回日期： 2016-01-27

作者简介：李逸(1993-)，男，湖南汨罗人，硕士研究生，研究方向为岩土工程可靠度(Email：1427648137@qq.com)

基金项目：国家自然科学基金(51278217)

中图分类号：TU457

文献标识码：A

文章编号：2095-0985(2016)03-0094-05