重复性建设项目赶工问题

张立辉，　梁洪源

(华北电力大学　经济与管理学院， 北京　102206)



重复性建设项目赶工问题

张立辉，梁洪源

(华北电力大学经济与管理学院， 北京102206)

摘要：压缩正控制子工序的工期，是处理重复性建设项目赶工问题的常用手段，但这类方法将产生较大的项目总费用。本文提出了重复性建设项目赶工问题新算法。算法为项目中的正控制子工序和逆控制子工序，分别制定相应的调整方案，每一步调整将挑选出对应总费用增加率最小的方案，直至达到预定的工期，确保项目能以最小的费用实现赶工。此外，本文提供判别控制子工序类别的新方法，用以判定出控制子工序的类别。算例分析结果显示，本文算法能简便识别出各类型控制子工序，并以较小的计算量得到对应最小总费用精确解。

关键词：重复性项目；控制子工序；项目总工期；赶工

重复性建设项目是由多个重复单元组成的项目，其中的每个单元都具有相同的工作。如高速公路工程、房屋工程、桥梁工程等，需要在多个不同的单元里重复进行相同的工作，这类建设项目就属于重复性项目。通常情况下，将重复施工的单元集合称为工序，工序在某个特定单元的部分称为子工序[1]。传统的项目调度问题，常用关键路径法(CPM)来解决。但是，当处理重复性项目时，CPM网络就会存在许多的不足[2]，主要表现在：(1)难以确保资源的连续性[3]；(2)无法显示两个工序之间的距离约束[4]；(3)各子工序的工作效率无法体现[5]。针对这些不足，常用线性调度法(LSM)[6]、重复性调度法(RSM)[3]以及平衡线法(LOB)[7]等方法处理重复性项目调度。本文将使用RSM来表示重复性项目，该方法在二维坐标中用纵轴表示时间，横轴表示各单元子工序。

处理赶工问题的核心目标，是要使得调整后的项目总工期达到预定的最晚总工期。由于在所有的CPM网络图中都存在关键路径，对关键路径上的工序进行适当的压缩，能够缩短项目的总工期，因此在处理一般项目的赶工问题时，主要采取对CPM网络中的关键工序进行工期压缩的方式。RSM中存在着与CPM的关键路径相似的路线，称为控制路线，位于控制路线上的子工序称为控制子工序。一般情况下，可以将控制子工序分为两类：正控制子工序和逆控制子工序[1]。对正控制子工序工期进行适当压缩，可以达到减少项目总工期的目的；与之相反，对逆控制子工序工期进行适当延长或者引入间断时间，反而能够缩短项目总工期。除总工期之外，重复性项目赶工问题还需要考虑项目的总费用。项目的总费用通常可以分解为直接费用、间接费用以及资源闲置费用。整个项目所有子工序的直接费用总和即为项目的直接费用，每个子工序的工作量及工作效率不同，将导致各子工序的直接费用有所差别。间接费用是间接为项目服务而产生的费用，通常与总工期成正比例关系[8]。资源闲置费用由项目停工期间的照常支付的设备租赁费、劳务费等组成，通常与间断时间成正比。

本文探讨的重复性项目赶工问题，是重复性项目“时间-费用”权衡中的子问题，其实质是在最晚总工期确定的前提下，给出总费用最小的赶工方案。许多学者曾利用模型规划的方法来处理重复性项目赶工问题。例如，Reda[9]曾提出一个数学规划模型，该模型以项目总工期早于最晚总工期为条件，以项目总费用最小为目标，对赶工问题进行求解。Sonouci等[10]利用动态规划来求解最优赶工方案，这类方法需要较大的计算量，不适合大型项目的计算。

随着计算机应用的不断深入，有许多学者将人工智能算法应用到重复性项目的赶工问题中。例如，Hegazy等[11]将CPM与LOB相结合，并利用遗传算法来搜索优化方案。Long等[12]基于遗传算法，对总工期与总费用之间的不同权值，给出不同的最优赶工方案。Hegazy等[13]则将软逻辑应用到赶工问题中，以求解最优方案。通常情况下，智能算法只能得到问题的近似解，而且需要较大的计算量，当问题的规模增大时将面临较大的求解难度。Hamid等[14]将CPM与LOB相结合来处理赶工问题，该方法在问题规模增大的情况下同样面临着较大的计算量。Liu等[15]将外包资源引入到重复性项目调度中，但该方法实际上只考虑对工序工期进行压缩，这将产生较大的项目总费用。

本文将首先从理论上分析不同类型的控制子工序对重复性项目总工期的影响，并提出一种能更简便地判断出各控制子工序类别的方法。算法为正控制子工序和逆控制子工序分别制定相应的调整方案。每次调度调整挑选出总费用增加率最小的方案，能确保最优调度的总费用最小。最后，利用一个桥梁建设的案例，展示本文算法在处理赶工问题中的优势。

1控制子工序的类型及判定

根据控制子工序的类别，为其分别提供相应调整方案，是本文算法能否顺利进行的关键一步。正确选择每一步所需调整的子工序，并对其进行相应的调度调整，才能确保项目能顺利达到赶工目的。为此，本节将从理论上分析不同类型控制子工序工期的变化对项目总工期和总费用的影响，并提出一种确定控制子工序类别的新方法。

1.1控制子工序的类型

正控制子工序的性质类似于CPM网络中的正关键子工序，对这类子工序的工期进行适当压缩，在使得该子工序工期缩短的同时，还能缩短项目的总工期[16]。但压缩子工序工期需要引入更多的资源，将会增加较多项目总费用。在重复性项目调度中，当某一子工序处于控制路线上，且具有比其紧前子工序和紧后子工序更低的效率时，它就是一个正控制子工序。如图1所示，b是一个正控制工序，假设各工序间存在“结束-开始”时间约束。适当压缩工序b的工期，可使得工序c的开始时间提前，最终导致项目总工期缩短。

图1　压缩正控制工序

逆控制子工序是重复性项目中一种常见的工序，它具有与正控制子工序相反的性质，适当延长它的工期，反而会缩短项目的总工期[1]。利用逆控制子工序的这一特性，我们可以通过适当降低逆控制子工序工作效率的方式，使项目总工期缩短，同时还能减小项目总费用的增加量。在重复性项目调度中，当某一子工序处于控制路线上，且具有比其紧前子工序和紧后子工序更高的效率时，它就是一个逆控制子工序。如图2所示，工序b是逆控制工序，假设各工序间存在“结束-开始”时间约束。对工序b的工期进行适当延迟后，工序b的开始时间可以提前，使得工序c的开始时间提前，最终导致项目总工期缩短。

图2　延迟逆控制工序

在两个连续的逆控制子工序单元之间适当引入间断时间，同样可以达到缩短项目总工期的效果。如图3所示，假设各工序间存在“结束-开始”时间约束，逆控制工序b包含三个连续的子工序单元，在工序b之间引入间断时间，可以使得工序b的开始时间提前，并使得工序c的开始时间提前，最终导致项目总工期缩短。由于引入间断时间会导致人员及设备的闲置，这将增加资源闲置费用，从而在一定程度上增加项目总费用。

图3　逆控制工序中引入间断时间

1.2控制子工序类型的判别方法

首先要根据已有方法来确定调度中的控制路线，处在控制路线上的子工序即为控制子工序[17]。在项目调度的调整阶段，任何控制子工序的工期变化都有可能导致控制路线发生改变，使得最终的项目总工期发生改变。当我们搜寻出调度中的控制路线之后，本小节将通过对控制路线上每一个子工序与其紧前子工序、紧后子工序的开始时间和结束时间进行对比计算，求解出每一个控制子工序的V值，并根据该值的正负性，判定控制子工序的类别。式(1)～(6)将说明如何判定控制子工序的类型。

Li,j=Si,j-Si-1,j

(1)

Ri,j=Fi,j-Fi-1,j

(2)

Vi,j=Ri,j-Li,j

(3)

Li+1,j=Si+1,j-Si,j

(4)

Ri+1,j=Fi+1,j-Fi,j

(5)

Vi+1,j=Ri+1,j-Li+1,j

(6)

式中：Si,j、Si-1,j、Si+1,j为子工序ai,j、ai-1,j、ai+1,j的开始时间；Fi,j、Fi-1,j、Fi+1,j为子工序ai,j、ai-1,j、ai+1,j的结束时间；Ri,j为子工序ai,j与其紧前工序ai-1,j结束时间的差值；Ri+1,j为子工序ai,j与其紧后工序ai+1,j结束时间的差值；Li,j为子工序ai,j与其紧前工序ai-1,j开始时间的差值；Li+1,j为子工序ai,j与其紧后工序ai+1,j开始时间的差值；Vi,j为Ri,j与Li,j的差值；Vi+1,j为Ri+1,j与Li+1,j的差值。

当Vij>0且Vi+1,j<0时，可判定ai,j是正控制子工序；当Vij<0且Vi+1,j>0时，可判定子工序ai,j是逆控制子工序。特别地，位于第一道工序或最后一道工序上的控制子工序属于正控制子工序。

图4呈现了一个典型的重复性项目，该项目包含5道工序，每道工序内有4个单元的子工序。图中加粗部分为该调度的控制路线。对于子工序a2,1，由于该子工序处于控制路线上，且V2,1<0，V3,1>0，我们可以判定：子工序a2,1为逆控制子工序；对于子工序a3,3，由于该子工序处于控制路线上，且V3,3>0，V4,3<0，我们可以判定子工序a3,3为正控制子工序。

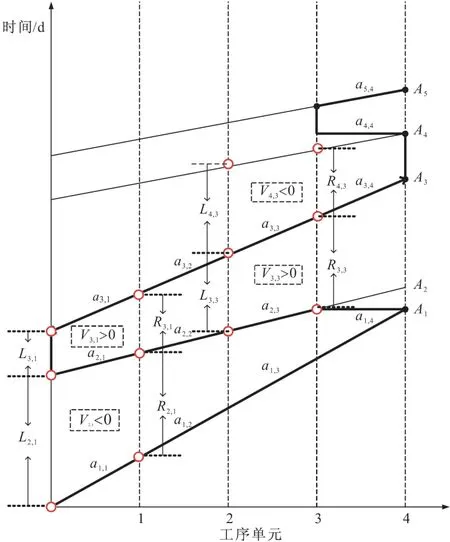
图4　子工序类型判别

2总费用增加率计算方法

在实际工程中，赶工问题不仅要使项目总工期满足小于最晚工期的要求，还需要对调度改变所引起的项目总费用变化进行思考。通常情况下，项目总费用由直接费用和间接费用以及闲置资源费用构成。直接费用一般包含材料费用、劳工费、设备费用等，本文将各子工序的材料费用、劳工费、设备费用等各费用整合为各子工序的直接费用。间接费用则与项目总工期成正比。每道工序的闲置资源费用则与该工序的间断时间总和成正比，所有工序的闲置资源费用总和即为项目的闲置资源费用。项目总费用可由式(7)～(10)计算。

(7)

IC=T×ICR

(8)

IRC=IT×IRCRi

(9)

TC=DC+IC+IRC

(10)

式中：DCi,j为子工序ai,j的直接费用；DC为项目的直接费用；IC为项目的间接费用；T为项目总工期；ICR为间接费用率；IRCRi为第i道工序的闲置资源费用率；IT为项目的间断时间总和；IRC为项目的闲置资源费用；TC为项目总费用。

在赶工过程中，当对控制子工序ai,j进行适当调整时，该项目的直接费用、间接费用以及资源闲置费用将可能发生改变。产生的新调度方案所对应的各项费用计算方法如式(11)～(14)所示。由于项目总费用的计算量主要产生于子工序直接费用累加的过程，因此，通过叠加增量的方式求解新方案直接费用，能在一定程度上减小计算复杂度。

DCn=DC+ΔDCi,j

(11)

ICn=Tn×ICR

(12)

IRCn=IRC+ΔIT×IRCRi

(13)

TCn=DCn+ICn+IRCn

(14)

式中：DCn为新调度方案的直接费用；ΔDCi,j为子工序ai,j直接费用的增加量；ICn为新调度方案的间接费用；Tn为新调度方案总工期；ΔIT为间断时间增加量；IRCn为新调度方案的闲置资源费用率；TCn为新调度方案的项目总费用。

式(15)给出了总费用增加率的计算方式，该值越小，意味着项目赶工的代价越小，该调度调整方案的可接受性就越强。

Ω=(TCn-Tn)/(T-Tn)

(15)

式中：Ω为总费用增加率。

3重复性项目赶工问题新算法

重复性项目的赶工问题是指：某一重复性项目的初始调度项目总工期为T，由于项目各方的要求，项目需要在D时刻(最晚工期)之前完工。因此，需要通过对初始调度进行调整，使得项目总工期T满足式(16)的要求。

T≤D

(16)

赶工算法需要解决的问题是：对于给定的不满足最晚工期要求的初始调度，确定具体的赶工方案，使得最终的调度在满足式(16)的前提下，达到项目总费用最小的目标。

3.1算法思想

图5展示了本文算法的总体思想，算法着重利用正控制子工序与逆控制子工序的特性，对项目进行有针对性的调度调整。相对于已有的算法，本文算法能以较小的计算量得到赶工问题的精确解，且求得的最优调度所对应的项目总费用也最小。

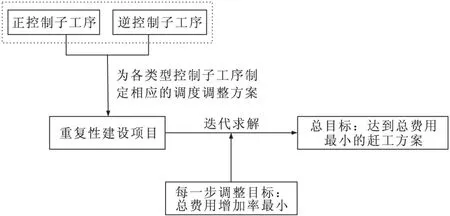
图5　本文算法总体思想

新算法以迭代运算的方式进行调度调整，每一次迭代将单独对项目中的某一个控制子工序进行调整。在每一次迭代中，首先利用本文提供的方法，判定出最新调度控制路线上的每一个控制子工序的类别。紧接着，算法对最新调度内的每一个正控制子工序的工期，在不超过其最短工期的范围内分别进行所有可行的加速调整，保留能使总工期减小的方案；对最新调度的每一道逆控制子工序，在不超过其最长工期的范围内分别进行所有可行的延长调整，保留能使总工期减小的方案；对最新调度中两个连续的逆控制子工序，在不超过最大间断时间的范围内，在两者之间引入所有可行的间断时间，保留所有能使总工期减小的方案。最后，结合文中提出的总费用增加率Ω的计算方法，从被保留的调整方案中，挑选出对应项目总费用增加率最小的方案，并将该方案存储为最新调度，本步迭代调整完成。

算法重复进行上述迭代运算，直至最晚工期达成。由于控制子工序的数量是有限的，而且每一个子工序可供调整的方案也是有限的，因此，单独针对每一道控制子工序进行每一步迭代调整，使得项目能以较小的计算量求解出最优赶工调度方案。

3.2算法步骤

图6是本文算法的流程图，具体步骤总结如下：

(1)初始化，输入信息，将初始调度存储为最新调度。

(2)查找最新调度中的控制路线，计算最新调度中各控制子工序的V值，由此判别出控制子工序的类型，进入(3)。

(3)判断是否存在工期大于最短工期的正控制子工序(可加速的正控制子工序)，或者工期小于最长工期的逆控制子工序(可延迟的逆控制子工序)，或者间断时间小于最大间断时间的两个相邻的逆控制子工序(可间断的逆控制子工序)。若是，进入(4)；若否，进入(8)。

(4)对可压缩的正控制子工序，在不小于其最短工期的范围内，分别进行所有可行的压缩调整；对可延长的逆控制子工序，在不大于其最长工期的范围内，分别进行所有可行的延长调整；对可间断的逆控制子工序，分别引入所有可行的间断时间。转入(5)。

(5)判断步骤(4)中是否存在能使总工期减小的方案，若是，保留所有能使总工期减小的调整方案，进入(6)；若否，进入(8)。

(6)分别计算所有保留方案的总费用增加率，挑选出对应总费用增加率最小的方案，存储为最新调度。进入(7)。

(7)判断项目总工期是否小于最晚工期。若是，则转入(8)；若否则转入(1)。

(8)调整结束，输出最优调度。

图6　算法流程

3.3算法优势

相比较于已有的算法，本文算法在处理重复性项目赶工问题时具备如下优势：

(1)利用文中提出的方法，能简便的识别出项目中存在的正控制子工序和逆控制子工序。在调度调整时，为正控制子工序和逆控制子工序提供相应的调整方案，使得调整更具针对性。

(2)由于项目中的正控制子工序和逆控制子工序数量是有限的，且各子工序可供选择的调整方案也是有限的，因此，相比较于传统的对所有工序分别进行压缩再挑选的方法，本文算法计算量较小，且能得到精确解。

(3)直接调整控制子工序工期的方式较为直观，便于项目调度人员理解。调度人员可以灵活的运用各种措施，来实现最优调度方案。

4算例分析

本文用一桥梁建设项目案例来说明新算法的优势。该项目共由五道工序组成：打桩(A)、路基修建(B)、桥墩建设(C)、主梁(D)、桥面铺设(E)，如图7所示，每道工序都包含四个单元的子工序，同一工序内的不同子工序工作量略有不同，各工序之间存在“结束-开始”约束关系，同一工序内的相邻两个单元的子工序至少需要1 d的时间间隔。

图7　桥梁建设项目

4.1算法优化结果

表1给出每个子工序的不同工期所对应的直接费用，项目的间接费用率为800元/d。表2给出了各道工序内相邻两个子工序之间的最大间断天数，以及每道工序的闲置资源费用率。表3给出了各工序的所有子工序初始调度的工期，并为各子工序提供工期调整的变化范围，当某个子工序需要调整时，可以在最短工期到最长工期之间选择调整(这里规定各子工序工期只能取整)。通过计算，得到项目初始调度总工期为145 d，初始调度总费用为1586640元。

表1　子工序不同的工期所对应的直接费用　元

表2　各工序允许的最大间断时间及闲置资源费用率

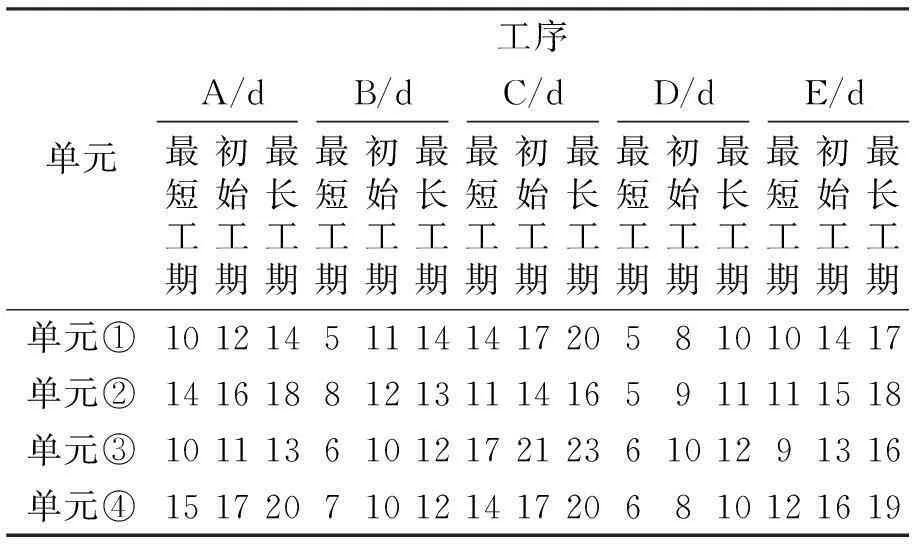
表3　各子工序初始调度工期及其最短和最长调整工期

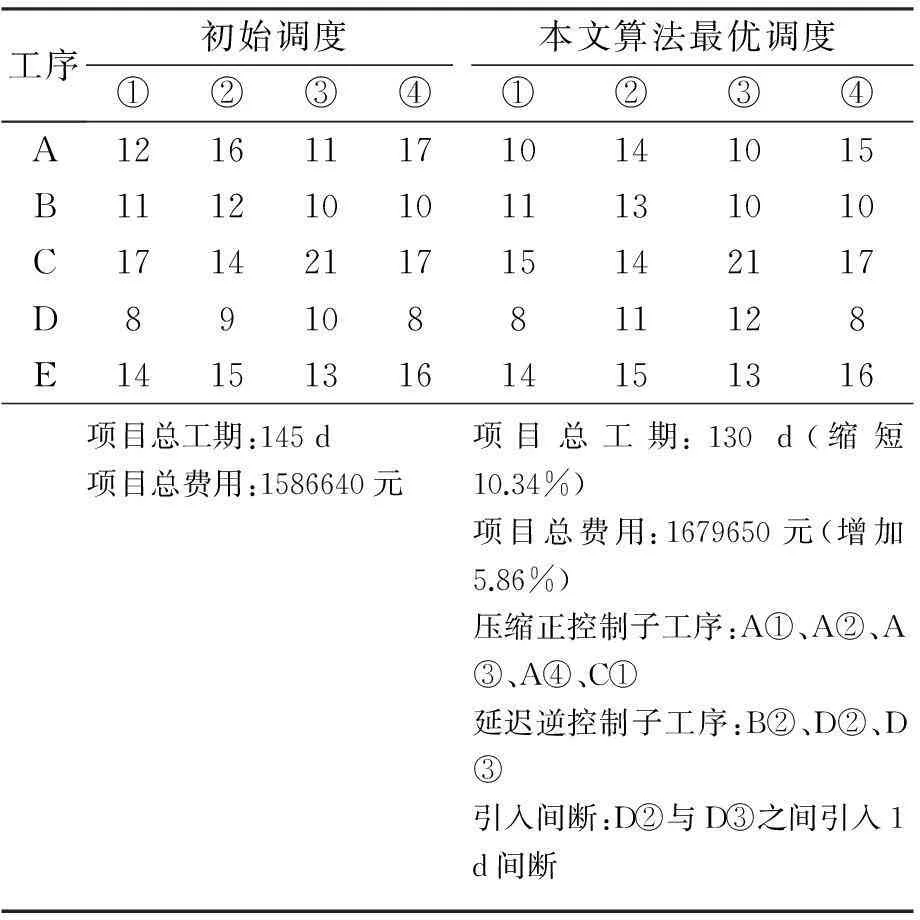
由于投资方的要求，项目必须在130 d之内完工，因此需要对项目进行赶工。利用本文算法对项目进行赶工计算，针对不同的控制子工序类型采取相应调整措施，得到最优调度的项目总工期为130 d，刚好满足业主要求，最优调度所对应的项目总费用为1679650元。图8为初始调度与利用本文算法求得的最优调度之间的对比。

表4给出了本文算法赶工优化结果。通过表4可以发现，本文算法在赶工的过程中，共进行了9步迭代调整，分别对A①、A②、A③、A④、C①等五个正控制子工序进行了工期压缩，对B②、D②、D③等三个正控制工序进行工期延迟，并在D②、D③之间引入了1 d的间断时间。经过如上调整，使得工期较之初始调度在缩短10.34%的同时，项目总费用仅仅增加了5.86%。此外，本文算法计算量较小，利用MATLAB软件处理本例题计算时，用时不到1 s即可得到精确解。

图8　调度对比

d

4.2与传统算法相比较

若使用传统赶工方法，即压缩子工序工期的手段，在调整过程中仅考虑对正控制子工序进行压缩，每一步调整挑选对应总费用增加率最小的调整方案，逐步调整直至达到最晚工期的要求。

调度调整结果如表5所示，通过分析表格数据可以发现，传统算法在赶工的过程中，仅仅对A①、A②、A③、A④、C①、C②、C③等七个正控制子工序进行了工期压缩，不考虑其他方式。最终达到130天的工期要求时，所对应的最优调度总费用为1750460元，较之初始调度增加了163820元。由此可见，本文算法着重利用不同类型的控制子工序对项目总工期的影响，使得总工期在缩短15天的同时，比传统压缩正控制子工序的方法节省了70810元，总费用增加量减少近一半。

表5　本文算法与传统算法对比　d

5结束语

赶工问题是重复性建设项目调度中的一类常见问题。由于重复性项目调度中的控制子工序严重影响着项目总工期，因此，本文着重利用此关系，构造赶工问题的新算法，使得项目能在达到合同工期的同时，最大程度地减小项目总费用。文中首先从理论上分析了控制子工序对重复性项目总工期的影响，针对正控制子工序和逆控制子工序提出了不同的赶工策略。并提出了一种新的确定控制子工序类别的方法，该方法能更简便地判断出控制路线上各子工序的类别。判别出各子工序的类别之后，本文算法分别对控制路线上的各类型控制子工序进行有针对性的调整。每一步调整将挑选出总费用增加率最小的赶工方案，从而确保项目能以最小的总费用达到赶工的目的。最后，利用一个桥梁建设案例，展示本文算法能以较小的计算量和最小的总费用求得最优调度的优势。由于控制子工序对重复性建设项目的工期和费用有着重要的影响，笔者将在今后加强对控制子工序的研究。

参考文献

[1]张立辉, 邹鑫. 重复性项目调度理论与方法研究[M]. 北京： 中国电力出版社，2012.

[2]Selinger S. Construction planning for linear scheduling optimization[J]. Journal of Construction Division, 1980，106(2)： 195-205.

[3]Harris R B，Ioannou P G. Scheduling projects with repeating activities[J]. Journal of Construction Engineering and Management，1998，124(4)： 269-278.

[4]Kallantzis A，Lambropoulos S. Correspondence of activity relationships and critical path between time-location diagrams and CPM[J]. Operational Research，2004，4(3)： 277-290.

[5]Kallantzis A，Soldatos J，Lambropoulos S. Linear versus network scheduling: a critical path comparison[J]. Journal of Construction Engineering and Management，2007，133(7)： 483-491.

[6]Johnston D W. Linear scheduling method for highway construction[J]. Journal of the Construction Division，1981，107(2)： 247-261.

[7]Lumsdem P. The Line-of-balance Method[M]. Oxford：Pegamon Press，1968.

[8]Hyari K H，El-Rayes K, El-Mashaleh M. Automated trade-off between time and cost in planning repetitive construction projects[J]. Construction Management and Economics，2009，27(8)： 749-761.

[9]Reda P M. PRM: repetitive project modeling[J]. Journal of Construction Engineering and Management, 1990，116(2)： 316-330.

[10]Senouci A B, Eldin N N. Dynamic programming approach to scheduling of non-serial linear project[J]. Journal of Construction in Civil Engineering，1996，10(2)： 106-114.

[11]Hegazy T, Wassef N. Cost optimization in projects with repetitive non-serial activities[J]. Journal of Construction Engineering and Management，2001，127(3)： 183-191.

[12]Long L D，Ohsato A. A genetic algorithm-based method for scheduling repetitive construction projects[J]. Automation in Construction，2009，18(4)： 499-511.

[13]Hegazy T，Elhakeem A，Elbeltagi E. Distributed scheduling model for infrastructure networks[J]. Journal of Construction Engineering and Management，2004，130(2)： 160-167.

[14]Hamid R Z D，Abbas A，Reza A. CPM/LOB scheduling method for project deadline constraint satisfaction[J]. Automation in Construction，2014，48： 107-118.

[15]Liu S S，Wang C J. Optimization model for resource assignment problems of linear construction projects[J]. Automation in Construction，2007，16： 460-473.

[16]李星梅，乞建勋，苏志雄. 自由时差定理与k阶次关键路线的求法[J]. 管理科学学报，2009，12(2)： 98-104.

[17]张立辉，邹鑫，乞建勋，等. 重复性建设项目中确定关键路线的方法研究[J]. 运筹与管理，2015，1(24)： 142-148.

Repetitive Construction Project Deadline Constraint Satisfaction Problem

ZHANGLi-hui,LIANGHong-yuan

(School of Economics and Management, North China Electric Power University, Beijing 102206, China)

Abstract:Compressing forward controlling segment’s duration is the common method to achieve the desired duration, however, it will have a large total project cost. A new algorithm for repetitive construction project to achieve the desired duration is proposed. The algorithm provides different scheduling adjustment plans for forward controlling segments and backward controlling segments. Every adjustment execution the plan which corresponding to the minimum total cost increase rate, until the desired duration is achieved, it can guarantee the total cost is minimum. In addition, a simple method to find the controlling segments is proposed. Example analysis shows the new algorithm can easily recognize the controlling segments, and obtain an exact solution with a small amount of calculation, meanwhile, the total cost of the optimal solution is smaller than the common algorithm.

Key words：repetitive construction project; controlling segment; project duration; deadline constraint satisfaction

收稿日期：2015-12-10修回日期： 2016-01-22

作者简介：张立辉(1974-)，男，湖南宁乡人，教授，博士，研究方向为项目调度与优化(Email：lhy15749@163.com)

基金项目：国家自然科学基金(71271081)

中图分类号：TU72

文献标识码：A

文章编号：2095-0985(2016)03-0022-08