基于Shapley值-仿真技术的工序工期预测
申建红, 孙小宁, 张云华
(青岛理工大学 管理学院, 山东 青岛 266520)
基于Shapley值-仿真技术的工序工期预测
申建红,孙小宁,张云华
(青岛理工大学管理学院, 山东青岛266520)
摘要:针对传统工期预测方法中对工序工期影响因素间相关性考虑不足的缺陷,利用随机数仿真工序工期影响因素的不确定性和Shapley值函数计算多因素间相关性的原理,将仿真技术和Shapley值函数相结合,计算出影响因素对工期的综合影响系数。并且根据每道工序工程量与单位时间完成工程量的比值准确计算出每道工序的理想化工期。在此基础上利用工期综合影响系数对其进行调整,建立一种新的工期预测模型。最后,以工程实例对工期预测模型进行验证,并建立4DBIM进度模型对施工进度进行三维可视化模拟对比,结果表明,文中方法对施工工期的预测效果精确,具有较好的实际指导意义。
关键词:工期预测;仿真技术;Shapley值;BIM
伴随着经济的发展和工程技术水平的提高,现代工程项目日趋大型化和复杂化加大了工程工期预测的难度。科学合理的工期预测方法是预防工程延误的重要手段。对此,国内外学者进行了大量的研究。Ökmen等[1]考虑工期影响因素发生的不确定性,使用随机数仿真技术对其进行研究;Ahuja[2]等开发了一种基于CPM的工期预测模型,通过估计影响因素对工序的不确定影响,预测项目工期;Salem[3]等提出工程项目的进度具有不确定性,依据多元线性回归模型与神经网络系统,对工程项目工序进度进行预测分析;国内学者[4~6]分别采用模糊网络分析方法、灰色系统理论方法、灰色Verhulst方法对工期影响因素的不确定性进行研究。但上述研究均对影响因素间的相关性考虑不足。而Wang等[7]提出运用随机数仿真影响因素对工期的影响值,证明了考虑影响因素间相关性的重要性;李军辉等[8]基于工期影响因素的不确定性和相关性,采用影响因素相关矩阵和随机数对工程工期仿真模拟,同时证明考虑影响因素不确定性和相关性的工期预测方法比只考虑因素不确定性的方法更加准确;但其只考虑了两种影响因素间的相互影响,并没有考虑多种影响因素间的相互影响。
对上述传统工期预测方法的研究表明,在进行工期预测时,对工期的不确定性及相关性进行综合考虑,是准确预测工期的关键。基于此,本文考虑了多种影响因素间的相互影响,采用Shapley值函数对工期影响因素的相关性进行分析,并与利用随机数仿真影响因素的方法相集成建立了工期预测模型;将文中建立的工期预测模型、传统只考虑两种因素相关性的工期预测模型,借助BIM技术,建立各自的BIM计划进度模型,与BIM实际进度模型进行三维对比,以验证文中方法的准确性。
1工期预测模型的构建
工期的影响因素有很多,归纳起来主要包括人的因素(r1),物资供应(r2),资金供应(r3),设计变更(r4),技术水平(r5),气候因素(r6)等六大因素。这些影响因素自身具有不确定性,各因素之间又存在相关性。本文主要针对上述六种影响因素建立其体现影响因素的不确定性和多种影响因素间的相关性的施工工期预测模型。
1.1构建工期预测模型
1.1.1影响效果矩阵
各影响因素对工期的影响可能导致3种结果,即提前完工、正常完工、延误完工。各种结果预期的概率分布范围可以由专家根据历史统计资料获得。经研究表明[9]在各种因素影响下的工期服从正态分布,通过由随机数产生器产生服从正态分布的满足(0,1)之间的随机数,仿真影响因素出现的概率大小G1n(g1,g2,…,gn);将此概率大小与预期的概率分布范围相比较,假设影响因素随机数间于“比预期结果好”的区间内,则表明工期提前完成;经比较可得出影响因素随机数产生的预期结果,表达式为:
(1)
则某施工段的n项影响因素的影响效果组成影响效果矩阵为Qn1=[q1,q2,…,qn]T。
1.1.2Shapley值函数
Shapley值函数[10]是合作博弈中重要的分配指标之一,它能够实现联盟总体利益在各成员之间的有效分配,该方法包含了属性间的相互作用,即包含了多因素间的相关性,模型表达式为:
(2)
式中:φi(υ)表示其它因素影响下的第i种影响因素的权重;|s|表示s联盟中的影响因素个数;υ(s)表示联盟s的效益;υ(s/i)表示联盟s中出去成员i后可取得的效益;w(|s|)表示这种贡献的加权因子;υ(s)-υ(s/i)表示因素i在每个包含因素的联盟s中的边际贡献率。将式(2)得出的φi(υ)组成权重矩阵为:
(3)
所得ψnn则为考虑影响因素不确定性和多因素间相关性下影响因素的权重。它作为模型中影响程度矩阵,用以代替传统只考虑两种因素间相关性的工期预测方法中相关系数矩阵与影响度矩阵的乘积。
1.1.3建立工期预测模型
本文首先假设各种影响因素的影响度为零的情况下,利用每道工序工程量与单位时间完成工程量的比值准确计算出每道工序工期,将此工期作为理想化目标工期TM;然后利用Shapley值考虑多因素间的相互作用的原理计算出各因素在其他因素影响下的权重,将其结果与随机数仿真工期影响因素结合,计算出影响工期的各因素综合影响系数;最后将理想化目标工期TM进行调整计算出预测工期TY。根据上述思路,本文建立的工期预测模型为:
(4)
式中:k代表施工工序;TY表示预测工期;TM表示理想化目标工期;tyk表示第k道工序预测工期;tmk表示第k道工序理想化目标工期;G1n、ψnn、Qn1表示工期综合影响系数。
该模型运用随机数仿真工期影响因素,考虑了多个影响因素间的相关性,为进一步考虑工期影响因素相关性的计算奠定了基础。
1.24DBIM模型进度对比
BIM(Building Information Modeling,即建筑信息模型)是创建并利用数字化模型对建设项目进行设计、建造及运营的全过程的管理、优化的方法和工具[11]。首先建立工程的3DBIM模型。分别利用文中工期预测方法和传统只考虑两种影响因素间相关性的工期预测方法计算出每道工序的工期,然后根据各工序前后的逻辑关系绘制出整个工程的进度计划;将进度计划作为一个时间纬度与3DBIM实体模型相关联,通过软件将空间和时间两种信息整合到一个可视的4DBIM模型中,可以直观地预演整个施工过程[12],最后将两种BIM计划进度模型和BIM实际进度模型作对比。
2工程案例
2.1工程概况及BIM模型
本工程为阳光家苑27号综合楼,总建筑面积25019.68 m2,占地面积1787.12 m2,建筑高度为42.5 m,地下一层,地上11层,主体为剪力墙结构,基础为筏板基础。3DBIM建筑模型如图1,项目目标总工期为 436 d。本案例以首层为例,考虑工程影响因素不确定性和相关性的情况下对首层进行研究。在不考虑影响因素对工期影响的前提下,计算得出首层的理想化目标工期TM为26 d。合同工期TC为33 d。首层每道工序的理想化目标工期tm分别为1、3、2、3、5、7、5 d。施工进度横道图见图2,本工程为已完工工程。
图1 3DBIM模型

图2 理想状态下进度计划横道图
2.2工序工期预测模型
2.2.1影响因素参数设定
根据首层绑扎柱钢筋工序实际情况,由专家结合众多工程历史数据,归纳总结出各影响因素不同的概率分布范围内产生的影响结果,用于对随机数进行量化(表1)。

表1 影响因素概率分布范围
2.2.2影响因素随机数矩阵
利用随机数产生器产生(0,1)之间的服从正态分布的随机数,并且使每组随机数的个数等于影响因素的个数。由产生器产生的第一组随机数为:
G1×5=[0.3780.0570.3920.7810.8570.345],将该组随机数与表1进行比较,根据式(1)得到第一组影响效果矩阵为:Q5×1=[ 0-10110 ]T,同理可以得到若干组随机数和影响效果矩阵,本文选用1000组,随机数和影响效果矩阵如表2所示。
2.2.3因素影响度矩阵和工序工期预测
由专家结合相关资料对首层绑扎柱钢筋工序施工时可能遇到的影响因素的权重进行打分,分别得出单因素影响度的大小和多因素相互影响下对工程首层绑扎柱钢筋工序的权重大小,原则为六种影响因素的权重和v1(s)+v2(s)+…+v6(s)等于1。如果多因素间存在相关性,则此多因素的权重和将大于本身之和,即v123(s)>v1(s)+v2(s)+v3(s)。如表3所示(例表中{1,2,3}表示r1、r2、r3三种影响因素相互影响下对工期的影响度大小)。

表2 随机数矩阵和影响效果矩阵
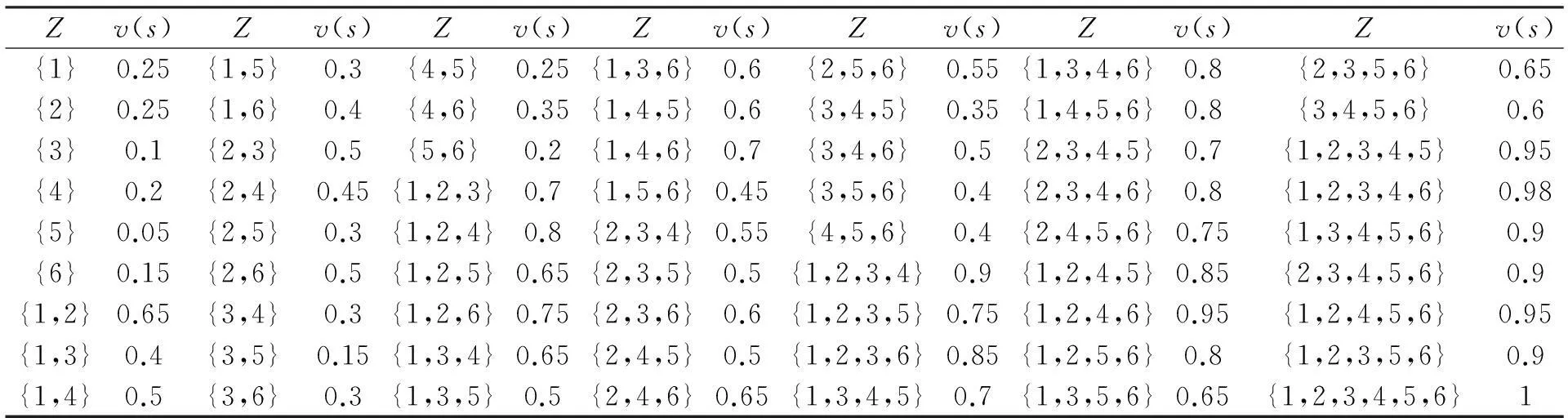
表3 因素影响度
注:Z表示影响因素的组合。
将表3数据代入式(2)中得出各因素的影响度大小(权重)分别为:φ1(υ)=0.240,φ2(υ)=0.249,φ3(υ)=0.122,φ4(υ)=0.187,φ5(υ)=0.048,φ6(υ)=0.144;得到因素影响度矩阵为:
ψ6×6=

根据以上数据,结合表2、式(4)得出的工序预测工期ty如表4所示。

表4 工序预测工期
由上述预测结果可得出工序工期预测直方图如图3所示。

图3 工序工期预测直方图
经计算得结合Shapley值方法的首层绑扎柱钢筋的工序预测工期为3.79 d,利用考虑两因素间相关性的预测方法得出首层绑扎柱钢筋的工序预测工期为3.86 d。对于一个标准的正态分布,其峰度系数和偏度系数分别为3和0。经计算知,结合Shapley值算法求得正态分布的峰度系数和偏度系数分别为3.23和0.43,而传统方法求得的系数分别为3.42和0.97,且图3b出现明显的右拖尾现象。结果表明结合Shapley值预测的工期更加满足正态分布。
同理,根据以上方法可以求出首层其他工序的预测工期。分别为1.26、3.79、2.52、3.64、6.3、8.82、6.3 d,首层的预测工期为32.53 d,且此工期小于合同工期。编制进度计划如图4所示。同理可编制出传统只考虑两种影响因素间相关性的预测方法的计划横道图。

图4 预测工期计划横道图
2.3基于 BIM工期模拟对比控制
以文中预测方法以及考虑两因素间相关性的预测方法分别建立4DBIM计划进度模型(如图5、6所示),通过将两种BIM计划进度模型和BIM实际进度模型(图7)对比,可以更直观地展现两种BIM计划进度与BIM实际进度的差别。
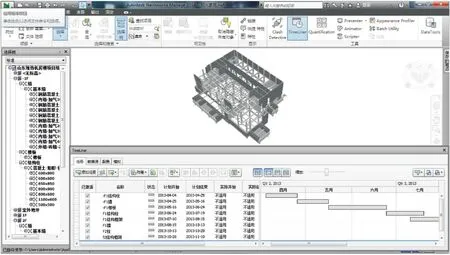
图5 文中方法BIM计划进度模型

图6 两因素相关性方法BIM计划进度模型
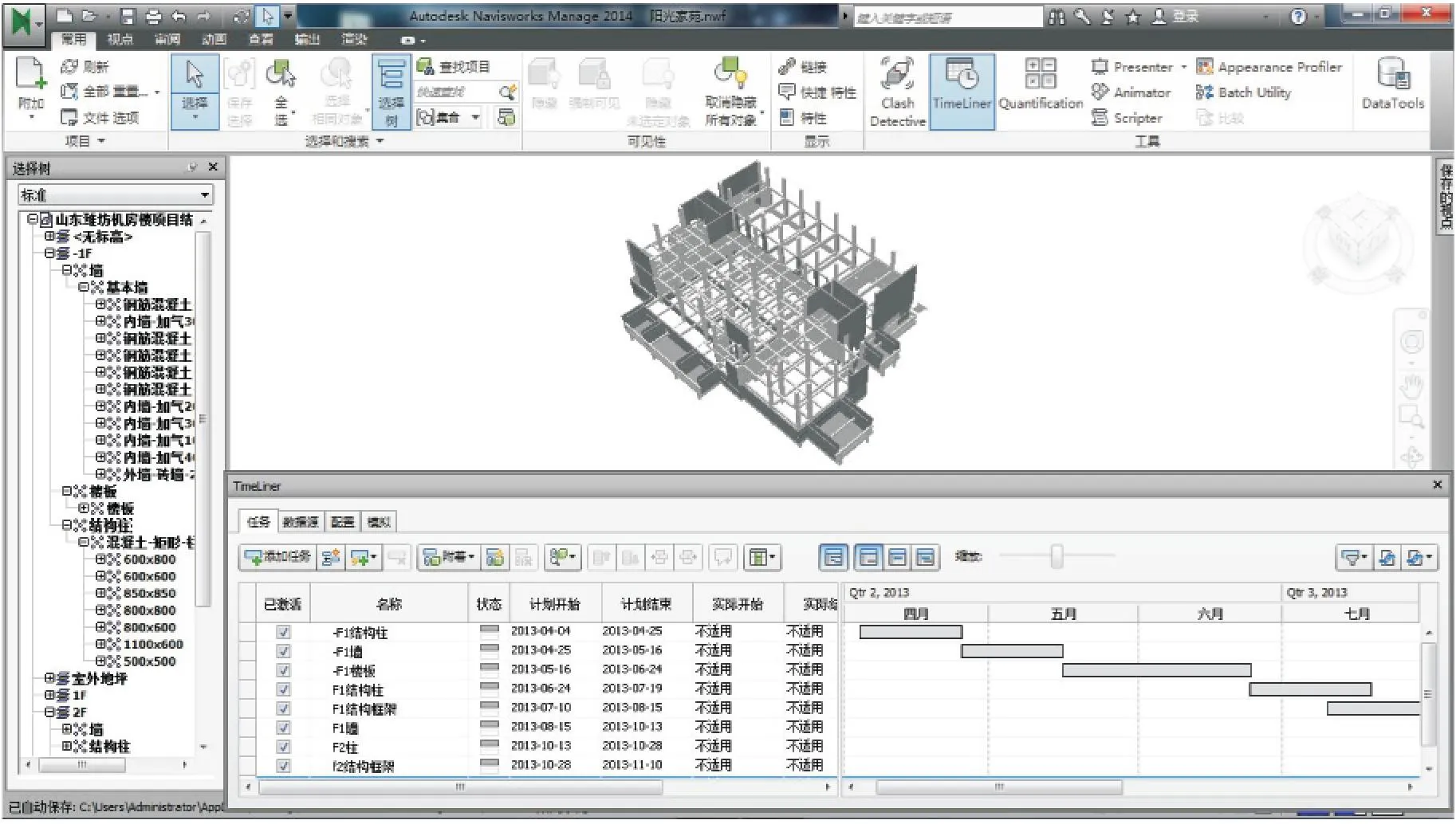
图7 BIM实际进度模型
由上图对比得知,文中方法预测的施工进度较传统方法预测的施工进度更加接近实际情况,表明文中方法更加准确。
3结论
(1)考虑了多个影响因素间的相互作用,建立了基于Shapley值的工期预测模型,该模型由于考虑了多因素间的相关性,在理论上更具有合理性。
(2)建立了4DBIM模型可以直观地对比三者可视化效果,是研究进度预测先进和有效的手段,对相关研究具有借鉴辅助意义。
(3)案例部分表明,利用随机数仿真工程工期影响因素和Shapley值相结合的方法预测工期可行且更准确。
参考文献
[1]Ökmenö,Özta A. Construction project network evaluation with correlated schedule risk analysis model[J]. Journal of Construction Engineering and Management,2008,134(1): 49-63.
[2]Ahuja H N,Nandakumar V. Simulation model to forecast project completion time[J]. Journal of Construction Engineering and Management, 1985,111(4): 325-342.
[3]Salem O,Solomon J,Genaidy A,et al. Site implementation and assessment of lean con struction techniques[J]. Lean Construction Journal,2005,2(2): 1-21.
[4]孟文清,张立宁,李万庆. 基于模糊网络的工程项目工期风险评估研究[J].河北建筑科技学院学报,2005,22(2): 73-75.
[5]刘英杰. 灰色系统理论在工程进度预测中的应用[J]. 东北水利水电,2006,24(4): 45-47.
[6]贾铭钰,杨秀芸,朱美洁,等. 基于挣得进度的灰色Verhulst模型对工程工期的动态预测[J]. 北京城市学院学报,2013,(5): 32-38.
[7]Wang W C,Demsetz L A. Application example for evaluating networks considering correlation[J]. Journal of Construction Engineering and Management,2000,126(6): 467-474.
[8]李军辉,张云波,祁神军,等. 基于风险相关性和随机性的工序工期预测模型[J]. 武汉理工大学学报(信息与管理工程版), 2010,32(6): 1018-1021.
[9]李林,李树丞,王道平. 基于风险分析的项目工期的估算方法研究[J]. 系统工程,2001, 19(5): 77-81.
[10]阮爱清,刘思峰,方志耕. 基于不确定性的shapley值模型及其风险研究[J]. 统计与决策,2009,(20): 15-17.
[11]Stephen A Jones. Introduction to BIM[EB/OL]. [2009-01-21]. http://bimhalcrow.wordpress.Com/2009/01/21/megraw-hill-construction-bim-smartmarkte-report/.
[12]王友群. BIM技术在工程项目三大目标管理中的应用[D].重庆: 重庆大学,2012.
Activity Duration Forcasting Based on Shapley-simulation Teconique
SHENJian-hong,SUNXiao-ning,ZHANGYun-hua
(School of management, Qingdao University of Technology, Qingdao 266520, China)
Abstract:Aiming at the defects that insufficient consideration of the correlation between the factors affecting the process duration in the traditional forecasting method,we use the uncertainty of the factors affecting random number simulated duration and the correlation between multiple factors of Shapley value function calculation,combine the simulation technique and Shapley function and then worke out the comprehensive influencing coefficiency of the influencing factor on the time limit. In addition,the ideal period for each process is calculated according to the ratio of the amount of each working procedure and the amount of unit time .Based on this, a new model for predicting the duration is established by using the comprehensive effect coefficient of the time limit to adjust it. Finally, the engineering projects are used to verify this model, and a 4D BIM progress model is established to simulate the construction progress. The results show that the proposed method has obvious forecast effect on the construction progress, and has better practical guiding significance.
Key words:the project duration prediction; simulation technique; shapley value; BIM
收稿日期:2015-11-28修回日期: 2015-01-04
作者简介:申建红(1970-),男,山东青岛人,博士,教授,研究方向为土木工程风场实测及结构抗风、工程项目管理(Email:sjhqwr@163.com)
基金项目:山东省自然科学基金(ZR2011GL021)
中图分类号:TU72
文献标识码:A
文章编号:2095-0985(2016)03-0030-05

