2016年中考数学模拟试卷（一）

一、 选择题

1. 下列四个数中，最小的数是（ ）.

A. 2 B. -2 C. 0 D.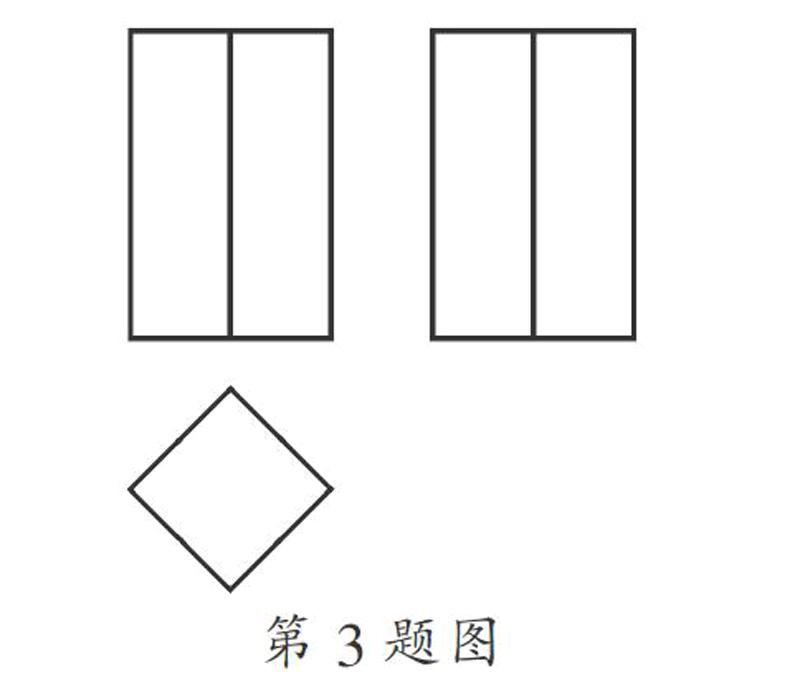

2. 4的平方根是（ ）.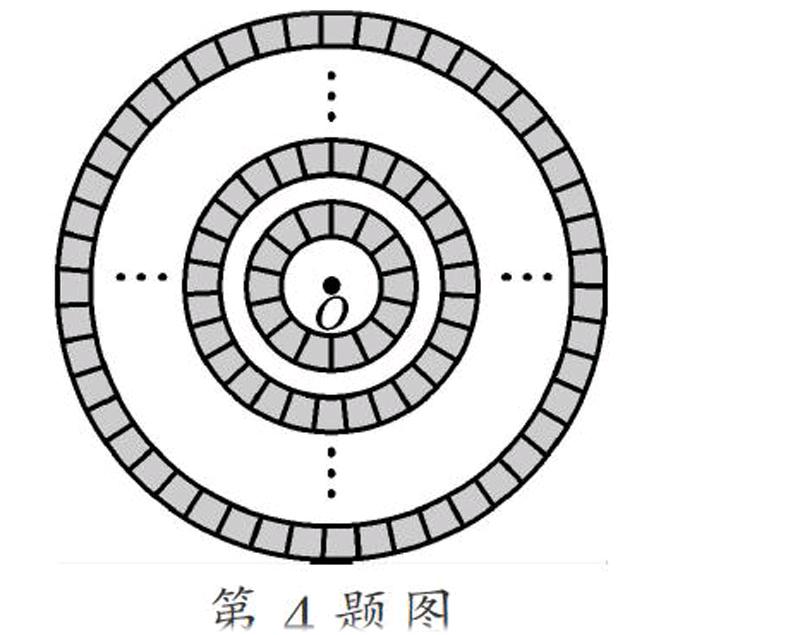

A. 2 B. 16 C. ±2 D.

3. 如图是一个几何体的三视图，则这个几何体是（ ）.

A. 正方体 B. 长方体 C. 三棱柱 D. 三棱锥

4. 如图，以点O为圆心的20个同心圆，它们的半径从小到大依次是1、2、3、4、……、20，阴影部分是由第1个圆和第2个圆，第3个圆和第4个圆，……，第19个圆和第20个圆形成的所有圆环，则阴影部分的面积为（ ）.

A. 231π B. 210π C. 190π D. 171π

5. 关于x的一元二次方程kx2+2x-1=0有两个不相等实数根，则k的取值范围是（ ）.

A. k>-1 B. k≥-1 C. k≠0 D. k>-1且k≠0

6. 如图，已知矩形ABCD中，AB=1，在BC上取一点E，将△ABE沿AE向上折叠，使B点落在AD上的F点，若四边形EFDC与矩形ABCD相似，则AD=（ ）.

A. B. C. D. 2

7. 如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，OA交小圆于点D，若OD=2，tan∠OAB=，则AB的长是（ ）.

A. 4 B. 2 C. 8 D. 4

8. 二次函数y=ax2+bx的图像如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）.

A. -3 B. 3 C. -5 D. 9

9. 如图，过点C（1，2）分别作x轴、y轴的平行线，交直线y=-x+6于A、B两点，若反比例函数y=（x>0）的图像与△ABC有公共点，则k的取值范围是（ ）.

A. 2≤k≤9 B. 2≤k≤8 C. 2≤k≤5 D. 5≤k≤8

10. 已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3在x轴上. 若正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3，则点A3到x轴的距离是（ ）.

A. B.

C. D.

二、 填空题

11. 写出一个比-3大的无理数是_______.

12. 已知1纳米=0. 000 000 001米，则2016纳米用科学记数法表示为______米.

13. 一个不透明的口袋中，装有红球6个，白球9个，黑球3个，这些球除颜色不同外没有任何区别，从中任意摸出一个球，则摸到黑球的概率为________.

14. 如图，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，点E的坐标_____.

15. 如图，在△ABC中，∠C=90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC=6，NC=2，则四边形MABN的面积是_______.

16. 观察下列一组数：，……，它们是按一定规律排列的，那么这一组数的第k个数是______.

17. 现有一张圆心角为108°，半径为40 cm的扇形纸片，小红剪去圆心角为θ的部分扇形纸片后，将剩下的纸片制作成一个底面半径为10 cm的圆锥形纸帽（接缝处不重叠），则剪去的扇形纸片的圆心角θ为______.

三、 解答题

23. 为了掌握我市中考模拟数学试题的命题质量与难度系数，命题教师赴我市某地选取一所成绩中等学校的初三年级进行调研，命题教师将随机抽取的部分学生成绩（得分为整数，满分为160分）分为5组：第一组85～100，第二组100～115，第三组115～130，第四组130～145，第五组145～160，统计后得到如图所示的频数分布直方图（每组含最小值不含最大值）和扇形统计图，观察图形的信息，回答下列问题：

（1） 本次调查共随机抽取了该年级多少名学生？并将频数分布直方图补充完整；

（2） 若将得分转化为等级，规定：得分低于100分评为“D”，100～130分评为“C”，130～145分评为“B”，145～160分评为“A”，那么该年级1500名考生中，考试成绩评为“B”的学生大约有多少名？

24. 如图，一次函数y=kx+b的图像与坐标轴分别交于A，B两点，与反比例函数y=的图像在第二象限的交点为C，CD⊥x轴，垂足为D，若OB=2，OD=4，△AOB的面积为1.

（1） 求一次函数与反比例函数的解析式；

（2） 直接写出当x<0时，kx+b->0的解集.

25. 已知，点P是△ABC边AB上一动点（不与A，B重合），分别过点A、点B向直线CP作垂线，垂足分别为E，F，Q为边AB的中点.

（1） 如图1，当点P与点Q重合时，AE与BF的位置关系是______，QE与QF的数量关系是______；

（2） 如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；

（3） 如图3，当点P在线段BA的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明.

26. 某文具商店销售功能相同的A、B两种品牌的计算器，购买2个A品牌和3个B品牌的计算器共需156元；购买3个A品牌和1个B品牌的计算器共需122元.

（1） 求这两种品牌计算器的价格；

（2） 学生毕业前夕，该商店对这两种计算器开展了促销活动，具体办法如下：A品牌计算器按原价的八折销售，B品牌计算器5个以上超出部分按原价的七折销售. 设购买x个A品牌的计算器需要y1元，购买x个B品牌的计算器需要y2元，分别求出y1、y2关于x的函数关系式；

（3） 小明准备联系一部分同学集体购买同一品牌的计算器，若购买计算器的数量超过5个，购买哪种品牌的计算器更合算？请说明理由.

27. 如图，已知抛物线与坐标轴分别交于A（-2，0）、B（2，0）、C（0，-1）三点，过坐标原点O的直线y=kx与抛物线交于M、N两点. 分别过点C、D（0，-2）作平行于x轴的直线l1、l2.

（1） 求抛物线对应的二次函数的解析式；

（2） 求证：以ON为直径的圆与直线l1相切；

（3） 求线段MN的长（用k表示），并证明M、N两点到直线l2的距离之和等于线段MN的长.