函数拟合法力数字传感器的非线性和温度补偿*

江　东, 单　薏， 刘绪坤， 王德玉

(哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨 150080)



函数拟合法力数字传感器的非线性和温度补偿*

江东, 单薏， 刘绪坤， 王德玉

(哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨 150080)

摘要:针对力数字传感器存在的分散性、非线性和温度特性问题，通过软件进行补偿。分析了力数字传感器的非线性特性，采用三次样条插值获得被测重力和输出频率的函数关系，将测量得到的输出频率通过三次样条插值计算得到被测重力。对于力数字传感器的温度特性，建立了分段三次插值函数，利用反函数得到不同温度下输出频率与被测重力的函数关系。将温度和频率量作为自变量，通过分段三次插值函数计算得到被测重力。函数拟合法实现力数字传感器的非线性和温度补偿使所需数据量减少。实测表明:该方法的测量精度高，非线性和温度补偿后的最大引用误差为0.5 %，满足实际工程的需要。

关键词:分散性； 非线性； 温度补偿； 函数拟合

0引言

力数字传感器可直接输出频率信号，极大方便了用户的使用。目前，直接输出数字量的Z型力传感器属于半导体器件，具有分散性、非线性和温度特性[1,2]，其输出频率和被测重力具有固定的关系，亦即具有可重复测量的特性，该特性使软件补偿具有可行性[3～6]。不同的力敏感元件输出频率与所测重力关系一般并不相同，且一般呈非线性关系，而且与温度有关[7～9]，因此，必须通过标定、非线性补偿和温度补偿方可实际应用。

传统的补偿方法有硬件补偿和软件补偿。其硬件补偿成本高，且电路复杂，调节困难，效果也不是很好，因此，一般较少采用；软件非线性补偿方法采用线性化最小二乘法实现补偿，但该方法误差较大，无法满足实际需要[10～12]。传统温度补偿方法，一般采用查表方法，欲达到精度要求往往表格数据量极大，不方便实际运用。

本文采用三次样条插值方法实现非线性补偿[13,14]，该方法精度高于最小二乘法线性补偿结果。通过实测不同温度下的输出频率对应的重力或通过计算重力与输出频率的反函数方法，采用分段三次插值函数实现温度补偿，所需数据量较小，且补偿精度更高，可以很好地解决力数字传感器存在的分散性、非线性和温度特性。

1力数字传感器的工作过程及其特性

力数字传感器的工作框图见图1。

图1　力数字传感器工作框图Fig 1　Working block diagram of force digital sensor

不同的力数字传感器具有不同的输出特性曲线，即fA(g)≠fB(g)，其中,g为被测重力，f为敏感元件输出频率，A,B为元件标号，表示不同元件。不同力敏元件输出频率与被测重力不同的特性即为半导体材料的分散性。

对于每一个力数字敏感元件，其函数关系一般为非线性关系，即具有半导体器件的非线性特性。

不同温度下，每个力敏感元件输出频率与被测重力的函数关系固定，但函数关系不同，即fA(g，T1)≠fA(g，T2)，T1,T2表示温度值，该特性即为力敏元件的温度特性。

上述分析表明，力敏元件不能直接使用，需进行补偿。补偿方法有硬件补偿和软件补偿。硬件补偿会增加成本，且补偿电路复杂，调节不便，补偿效果不好。因此，实际运用中很少采用。本文对软件补偿方法进行研究。

力数字传感器输出频率量，可直接通过频率测量电路得到与被测重力呈一定关系的数字量。

实验表明，力数字传感器输出的频率量和被测重力为非线性关系。实测6只力数字传感器在外加0～100N时的输出频率，见图2。

图2　力数字传感器的分散性Fig 2　Dispersion of force digital sensors

图2可见，力数字传感器的输出频率与被测重力呈非线性关系，需要通过补偿才能得到准确的被测重力。

2力数字传感器的非线性补偿

力数字传感器的输出特性见图3。

图3　力数字传感器的输出特性Fig 3　Output characteristics of force digital sensor

图3可见，该力数字传感器的输出特性为非线性。

传统方法采用最小二乘法，将实测点用最小二乘得到一近似直线，使得直线与被测数据的误差的平方和最小，即用直线近似实际的特性曲线。

为了便于比较，将最小二乘法和三次样条插值方法补偿曲线比较见图4。

图4　三次样条和最小二乘法比较Fig 4　Comparison of cubic spline and least squares method

实测点最小二乘法和三次样条插值方法补偿误差见表1。

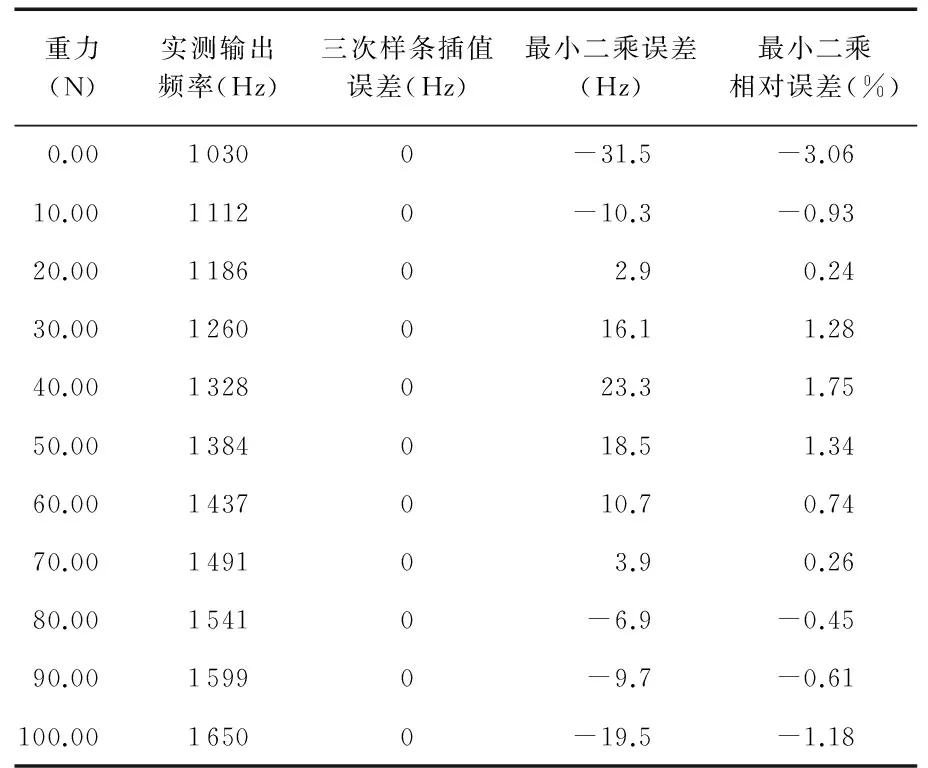
表1　三次样条插值法和最小二乘法误差比较

表1可见，三次样条插值方法在实测点处的误差为零，保证了补偿的精度。而最小二乘法实测点的最大误差在0 N和40 N处，误差分别为-31.5 Hz和23.3 Hz，这两点的相对误差也较大，可见采用三次样条插值法优于最小二乘法。

最小二乘法与三次样条插值法的差值，见图5。

图5　三次样条和最小二乘法比较差值Fig 5　Difference between cubic spline and least squares method

最小二乘法的误差由负误差变为正误差，然后又为负误差，重力在0,40 N时误差较大。

3力数字传感器的温度补偿

力数字传感器除了具有非线性特性以外还有温度特性，对于同一个传感器不同温度下一定压力对应的输出频率是不同的。

实测某力数字传感器在20～70 ℃时对应0～100 N的输出频率，见图6。

图6　不同温度下的输出特性Fig 6　Output characteristics at different temperatures

图6可见，不同温度下，力数字传感器输出频率与重力关系不是相同的一条曲线。因此，实际测量中测得的频率所对应的重力需要进行温度补偿。

为了实现力数字传感器的温度补偿，首先，应获得不同温度下一定输出频率所对应的重力。

可采用实测的方法，一定温度下调节不同的频率，实测所加的重力。如0 ℃时，1 000～1 900 Hz之间，间隔100 Hz时对应的重力。

本文通过求一定重力所对应的输出频率的反函数来得到一定温度下输出频率所对应的重力。先建立某温度下，一定重力所对应的输出频率的函数关系，然后求解该函数的反函数，表2给出了通过反函数计算方法得到的0 ℃时，1 000～1 900 Hz间隔100 Hz时输出频率所对应的重力。

表2　温度为0 ℃时输出频率与重力的关系

同此，10～100 ℃输出频率与重力的关系计算方法同上。

采用Matlab编程数值分析方法，采用分段三次插值，得到温度为0～100 ℃和力数字传感器的输出频率为900～1 900 Hz之间，对应的分段三次插值函数关系，见图7。

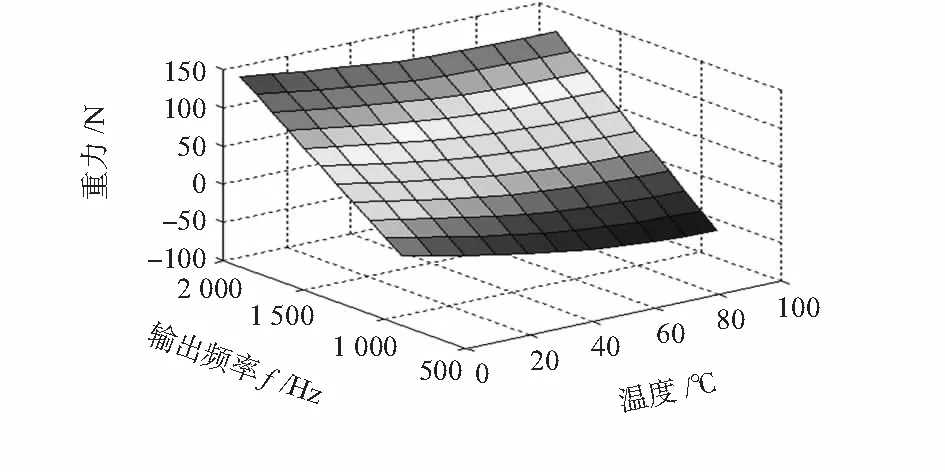
图7　非线性和温度特性补偿Fig 7　Nonlinearity and temperature characteristic compensation

上述分析过程对非线性和温度特性统一进行了补偿。为清楚了解非线性、温度与被测重力的等关系，给出力敏元件的等重力图，见图8。

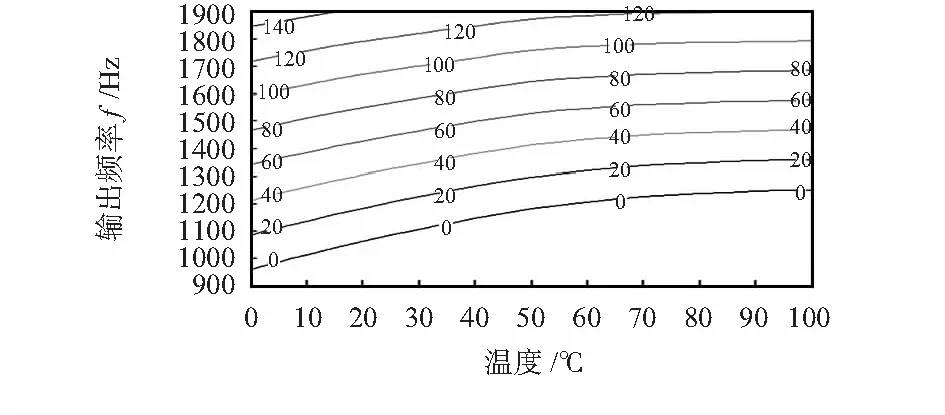
图8　力数字传感器的等重力线Fig 8　Equal gravity line of force digital sensor

在某温度下，通过实测力数字传感器的输出频率即可获得被测重力。

例如:在20 ℃，测得力数字传感器的频率为1 200 Hz，通过分段三次插值函数

g=interp2(x,y,z,20,1200,'cubicr').

运行后得到， 力数字传感器所受重力为22.780 N，与实测相符。同此，在其它温度下，只要测得力数字传感器的输出频率，即可得到被测的重力数值。

最后，补偿后的重力以频率形式输出，输出的频率与测得的重力函数关系见表3。

表3　输出频率线性标度变换

为了验证力数字传感器非线性和温度补偿效果，实测20 ℃时，0～100 N，力数字传感器的输出频率，见图9。

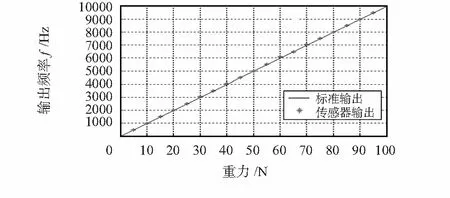
图9　补偿结果线性度Fig 9　Linearity of compensation results

图9非线性和温度补偿后的最大引用误差为0.5 %，满足实际工程的需要。

4结论

力数字传感器可直接输出频率信号,免去了A/D转换电路,极大地方便了用户的使用。但由于本质上力数字传感器属于半导体器件，具有分散性、非线性和温度特性，需要进行补偿。本文提出采用三次样条插值方法实现非线性补偿，该方法精度高于最小二乘法线性补偿效果；通过实测不同温度下的输出频率对应的重力或通过计算重力与输出频率的反函数方法，采用分段三次插值函数实现温度补偿，最后将测得的重力以线性频率量输出。该方法为力数字传感器的实际应用奠定了基础。

参考文献:

[1]葛辉，隋修武，王硕，等.超声波流量测量的误差分析与补偿方法研究[J].传感器与微系统，2015，34(10):38-40.

[2]毛亮亮，梁悦，王旭东.基于MLX90614的无线温度采集系统设计[J].电机与控制学报，2015，19(7):14-20.

[3]胡世军，刘学，王恩广，等.基于数控程序重构的加工中心误差软件补偿技术[J].机械制造，2015，53(4):79-81.

[4]刘一琦，李宁宁，傅裕，等.基于补偿分量的MMC最大调制系数的分析[J].电机与控制学报，2015，19(4):53-64.

[5]Wang Jingshu，Zhu Changan，Feng Mingchi，et al.Thermal error modeling and compensation of long-travel nanopositioning stage[J].International Journal of Advanced Manufacturing Technology，2013，65(4):443-450.

[6]Ho S Ping.Bid compensation decision model for projects with costly bid preparation[J].Journal of Construction Engineering and Management，2006，132(4):430-431.

[7]刘莉，邢华.基于无线传感器的瓦楞原纸温度监控系统设计[J].传感器与微系统，2015，34(10):90-92.

[8]赵怀功，段晨旭，丁旭东，等.数字式温度传感器的误差修正和软件补偿方法[J].山东科技，2015，28(5):97-100.

[9]钟君，蔡黎明，于涌.基于MLX90614的无线温度采集系统设计[J].传感器与微系统，2015，34(3):87-93.

[10] 于树海，王建立，董磊，等.基于最小二乘法拟合估计傅里叶望远镜的缺失分量[J].光学精密工程，2015，23(1):282-287.

[11] 刘冲，赵青，张桂臣，等.双注电子枪中最小二乘法拟合磁场的研究[J].电子学报，2015，43(7):1395-1398.

[12] 张熙胤，陈兴冲，王常峰，等.最小二乘法曲线拟合在桥梁施工应力监控中的应用[J].中外公路，2015，35(4):138-141.

[13] 林海波.基于机器视觉薄零件高精度测量技术的研究[J].压电与声光，2015，37(2):357-360.

[14] 江东,杨嘉祥,赵宏.Z-温度传感器的非线性补偿[J].传感器与微系统，2008，27(7):56-58.

Function fitting method for non-linear and temperature compensation of force digital sensor*

JIANG Dong， SHAN Yi， LIU Xu-kun， WANG De-yu

(College of Electrical & Electronic Engineering,Harbin University of Science and Technology,Harbin 150080,China)

Abstract:Aiming at problems of dispersion,nonlinear and temperature characteristics of force digital sensor,software is used to compensate.The nonlinear characteristics of force digital sensor are analyzed.Function relationship between gravity and output frequency is obtained by cubic spline interpolation,the measured output frequency is used to calculate the measured gravity.Temperature characteristics of force digital sensor piecewise cubic interpolation function is established,and function relationship between output frequency and measured gravity at different temperatures is obtained by inverse function.The temperature and frequency is used as independent variable,measured gravities is obtained by calculating piecewise cubic interpolation function.This method greatly reduces amount of data needed.Experimental results show that the measurement precision of this method is higher,the maximum reference error is 5 ‰ after non-linear and temperature compensation,which meets the needs of practical engineering.

Key words:dispersion; nonlinear; temperature compensation; function fitting

DOI:10.13873/J.1000—9787(2016)02—0016—03

收稿日期：2015—12—24

*基金项目：国家自然科学基金资助项目(51377037)

中图分类号:TU 352.1

文献标识码:A

文章编号:1000—9787(2016)02—0016—03

作者简介:

江东(1960-)，男，黑龙江哈尔滨人，博士，教授，研究方向为振动测量、传感器技术。