Euclid域中丢番图方程整数解的进一步讨论

邬　毅，张正萍，龙　兰

(重庆科技学院 数理学院，重庆　401331)



Euclid域中丢番图方程整数解的进一步讨论

邬毅，张正萍，龙兰

(重庆科技学院 数理学院，重庆401331)

摘要：研究了一个典型的丢番图方程在Euclid域中整数解的问题。利用二次域中的理论和二次代数整数环中的算术基本定理，得到了该方程的一般解法及其在Euclid域中所有整数解的相关结论，推广了前人研究的结果。

关键词：丢番图方程；Euclid域；整数解

1预备知识

关于丢番图方程

(1)

当D<0时，乐茂华[4]对于一般的D和p仅证明了当D≠4pr-1(其中r是正整数)时必有其解数N(D,p)≤2，而该方程在实二次域中的一般解法尚未给出。作为代数数论中的重要组成部分，二次域及二次域中的算术基本定理对研究该类方程的整数解有着重要作用。

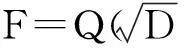
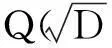
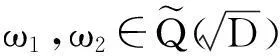
引理2[5]α∈A2(全体Q上的2次代数数组成的集合)的充要条件是

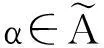
2r∈Z,r2-Ds2∈Z

引理3[5]设D满足引理2的条件，即

那么，α是二次代数整数的充要条件，可表示为

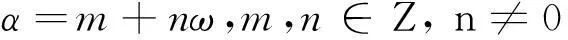
(2)

定理1[5]当D>1时，对每个D必有无穷多个形如式(2)的单位，具体如下：

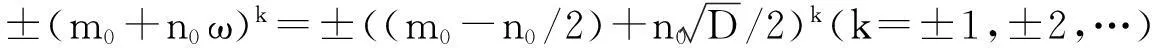
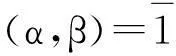
2主要结果的证明

首先证明当D=-21时，丢番图方程

(3)

仅有整数解(x,y)=(±5,1)。

证明丢番图方程(3)可以化为

(4)

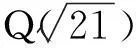
情形1

(5)

情形2

(6)

若式(5)成立，则有

故有

由此得到

24x=a5+210a3b2+2 205ab4=

a(a4+210a2b2+2 205b4)

以及

24=5a4b+210a2b3+441b5=

b(5a4+210a2b2+441b4)

(7)

由式(7)可得：b=±1或±2k，其中k=1,2,3,4。

① 若b=1，由式(7)得a4+42a2+85=0，显然方程没有整数解。

② 若 b=-1，由式(7)得5a4+210a2+457=0，此时方程也无整数解。

③ 若b=±2k，左边24≡24(mod25)，而右边b(5a4+210a2b2+441b4)≡0(mod25)，矛盾。从而丢番图方程(3)在形如式(5)的分解下无整数解。

若式(6)成立，当n=1时有

由此得到

故有

5a5+1 050a3b2+1 1025ab4+105a4b+

4 410a2b3+9 261b5=±25x

25a4b+1 050a2b3+2 205b5+a5+

210a3b2+2 205ab4=±25

解得a=±2,b=0，进而有(x,y)=(±5,1)。

由于当D<0且D≠4pr-1(其中r是正整数)时，丢番图方程(3)的解数N(D,p)≤2，从而当D=-21时丢番图方程(3)仅有整数解(±5,1)，证明完毕[4]。

参考文献：

[1]邬毅.关于不定方程x2+11=4y5的唯一正整数解[J].高师理科学刊,2006,26(2):7-8.

[2]邬毅,龙兰.Euclid 域中 Diophantus 方程的整数解[J].数学杂志,2015,35(4):1012-1016.

[3]张丽平.关于不定方程x2+7=4y3[J].长春工程学院学报(自然科学版),2007,8(1):84-85.

[5]潘承洞,潘承彪.代数数论[M].2版.济南:山东大学出版社,2001.

[6]郭小芳,李锋,宋晓宁,等.基于加权Euclid范数的MTS异常检测[J].计算机科学,2014,41(5):263-265.

[7]冯克勤.代数数论[M].北京:科学出版社,2000.

(责任编辑陈艳)

Further Discussion on the Integer Solutions of Diophantine Equation on Euclid Field

WU Yi, ZHANG Zheng-ping, LONG Lan

(College of Mathematics and Physics, Chongqing University of Science & Technology, Chongqing 401331, China)

Abstract:We studied the integer solutions of a typical Diophantine equation on the Euclid field. We obtained the general solving method of this class of Diophantine equations and all the integer solutions by some theories on quadratic fields and the fundamental theorem of arithmetic on the ring of quadratic algebraic integers. On the other hand, we generalized some results in previous research achievement.

Key words:Diophantine equation; Euclid field; integer solution

收稿日期：2016-02-15

基金项目：重庆市自然科学基金资助项目(cstc2013jcyjA10049)；重庆科技学院优秀中青年骨干教师公派出国(境)深造项目(2012)

作者简介：邬毅(1982—)，男，重庆人，硕士，讲师，主要从事数论研究。

doi:10.3969/j.issn.1674-8425(z).2016.05.023

中图分类号：O156.7

文献标识码：A

文章编号：1674-8425(2016)05-0132-03

引用格式：邬毅，张正萍，龙兰.Euclid域中丢番图方程整数解的进一步讨论[J].重庆理工大学学报(自然科学)，2016(5):132-134.

Citation format：WU Yi, ZHANG Zheng-ping, LONG Lan.Further Discussion on the Integer Solutions of Diophantine Equation on the Euclid Field[J].Journal of Chongqing University of Technology(Natural Science)，2016(5):132-134.