基于深度信念网络的手写数字识别方法研究
刘长明(滨州市科学技术情报研究所,山东 滨州 256600)
基于深度信念网络的手写数字识别方法研究
刘长明
(滨州市科学技术情报研究所,山东 滨州 256600)
摘 要:多隐层神经网络的学习一直是大家关注的热点问题,而传统的学习算法并不能很好地适应于多隐层神经网络学习。提出了一种基于受限玻尔兹曼机的学习算法,将多隐层神经网络的学习变为多个受限玻尔兹曼机的顺序学习。将该方法应用于手写数字识别问题,取得了较好的识别结果。
关键词:深度信念网络;受限玻尔兹曼机;模式识别
0 引言
对于维数较高的有向信念网络,根据给定的数据矢量推测隐层行为的条件分布是很难的,这也导致它们的学习非常困难。变分法(Variational methods)对条件分布真值采用简单的近似,但是近似是很不尽如人意的,特别是在最深的隐层。变分学习需要对所有的参数一起学习,随着参数数量的增加让学习时间规模变的很大。
针对上述问题,Hinton等提出了一种由受限玻尔兹曼机构成的深度信念网络。这种深度信念网络可以用一个快速贪婪学习算法来很快找到一组性能很好参数。可以进行无监督学习,推断速度快而且准确。本文将这种深度信念网络用于手写数字识别,并对其性能进行了讨论。
1 深度信念网络简介
深度信念网络由可视层、输入层及多个隐层组成。传统的神经网络中[1-2],当隐层较多的时候,反向传播等算法都不能很好的工作。在深度信念网络中,相邻的两层可以看作一个受限玻尔兹曼机[3-4],这样一个深度信念网络就可以看作多个串联在一起的受限玻尔兹曼机。每次深度信念网络的学习,都可以分解成每个玻尔兹曼机从下向上的顺序学习。
如图1所示,每个受限玻尔兹曼机包括一个可视层和一个隐层,每一层都由多个随机神经元组成。层间的神经元之间都有连接,而层内的神经元之间没有连接。每个神经元都具有两个状态——激活和未激活,可以用0和1表示,状态是根据概率来确定。
1.1 补充先验
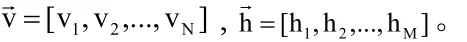
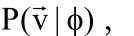
1.2 受限玻尔兹曼机的对比散度学习
当上述概率分布确定之后,需要根据此概率分布,确定在整个训练集(包含K个训练数据)上概率最大的使得φ,即
求φ*的关键是对L( φ)求偏导,可以将L( φ)表示为:
对φ中的某个参数φl求偏导为
这里,<.>P为依分布P的数学期望。上述方法称为对比散度学习算法[5]。
2 实验结果
MNIST手写数字数据库包括60000个训练图片和10000个测试图片。这个公开的数据库上,不同模式识别技术的结果都已经给出,所以评估新模式识别技术比较理想。在训练之前并不进行预处理和增强。网络在44000个训练图像上进行训练,将训练集分为440小批,每批包括每类数字的各10个图片。每个小批更新一次权重。
测试网络的一种方法是采用测试集,采用本生成模型来获得分类。对于测试集10000个测试图片,错误率1.29%。出错的125个数据如图2所示,在左上角给出了网络识别的结果。
每个训练周期的重构均方误差如图3所示。左侧是7层的网络,每层分别包括784、400、200、100、50、25、6个神经元。右侧是3层网络,每层分别包括784、532、6个神经元。从图中可以看出,7层网络的训练速度要明显高于3层网络,而且训练误差低于3层网络。
3 结论
本文讨论了一种深度学习的算法,将多隐层神经网络表示为一系列受限玻尔兹曼机串联的形式,而多隐层网络的学习相应的变为多个受限玻尔兹曼机的顺序学习。给出了受限玻尔兹曼机的对比散度学习方法。进而,将本方法应用到手写数字识别问题,取得了较高的识别率。
参考文献:
[1]叶世伟,史忠植.神经网络原理[M].北京:机械工业出版社,2006.
[2]Haykin S.神经网络与机器学习(英文版)[M].北京:机械工业出版社,2009.
[3]Jordan M, Sejnowski T. Learning and relearning in boltzmann machines [A]. Parallel Distributed Processing Explorations in the Microstructure of Cognition,1986:45-76
[4]Hinton GE. Training products of experts by minimizing contrastive divergence[J].Neural Computation,2002, 14(08):1711-1800.
[5]Hinton GE, Dayan P, Frey BJ et al. The wake-sleep algorithm for self-organizing neural networks[J].Science, 1995,268:1158-1161.
DOI:10.16640/j.cnki.37-1222/t.2016.12.112
作者简介:刘长明(1971-), 男,山东无棣人,本科,助理研究员,主要从事科学技术基础研究工作。

