Perfect 3-李代数的T-导子

白瑞蒲,高彦沙,张颖华

(河北大学 数学与信息科学学院,河北 保定　071002)



Perfect 3-李代数的T-导子

白瑞蒲,高彦沙,张颖华

(河北大学 数学与信息科学学院,河北 保定071002)

摘要:在3-李代数上定义T-导子的概念,得到了3-李代数的T-导子李代数TDer(L),对T-导子代数的结构进行了研究，并讨论了T-导子代数与导子代数和内导子代数的关系,证明了内导子代数是T-导子代数的理想在特征不为5的域F上的Perfect 3-李代数,它的内导子代数及导子代数在T-导子代数的中心化子为零.

关键词:3-李代数；T-导子；导子；内导子

MSC2010:17B05；17B30

3-李代数[1-2]在数学和物理学中有着广泛的应用[3-5]，特别是数域上的度量3-李代数为膜理论中的模型建立提供了重要依据[5-7].一个代数系统的导子代数在代数结构的研究中起着非常重要的作用.为了研究代数结构,研究者们在2-元代数系统上定义了导子、次导子、广义导子等概念[8-9].本文将在3-李代数上定义T-导子,并对其性质以及T-导子代数与导子代数和内导子代数的关系进行研究.

1预备知识

首先给出本文要用到的基本概念[9-11].

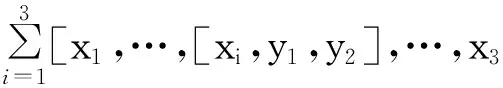
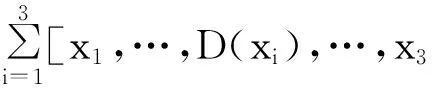
2主要性质

定义2设L是域F上的3-李代数,D是L→L的线性变换.如果对于∀x、y、u、v、w∈L有D[x,y,[u,v,w]]=[Dx,y,[u,v,w]]+[x,Dy,[u,v,w]]+[x,y,[Du,v,w]]+[x,y,[u,Dv,w]]+[x,y,[u,v,Dw]]成立,那么D叫做L的T-导子,记TDer(L)为所有T-导子的集合.

定理1对于任意的3-李代数L,TDer(L)是一个线性李代数.

证明:令D1,D2∈TDer(L),x、y、u、v、w∈l,只需验证[D1,D2]∈TDer(L)即可.根据定义2 直接计算可得[D1,D2]([x,y,[u,v,w]])=D1D2([x,y,[u,v,w]])-D2D1([x,y,[u,v,w]])=[[D1,D2]x,y,[u,v,w]]+[x,[D1,D2]y,[u,v,w]]+[x,y,[[D1,D2]u,v,w]]+[x,y,[u,[D1,D2]v,w]]+[x,y,[u,v,[D1,D2]w]],因此,[D1,D2]∈TDer(L).定理得证.

通过下面的例子,可以看出T-导子代数不等于导子代数.

例1设L是4维3-李代数,e1、e2、e3、e4是它的一组基.假设dimL1=2,L具有乘法表

[e1,e3,e4]=e2，[e2,e3,e4]=e1,[e1,e2,e3]=0,[e1,e2,e4]=0.

首先求出内导子李代数.由定义2和3-李代数L的乘法表直接计算可得ad(L)的一组基在3-李代数L的基e1、e2、e3、e4的矩阵为

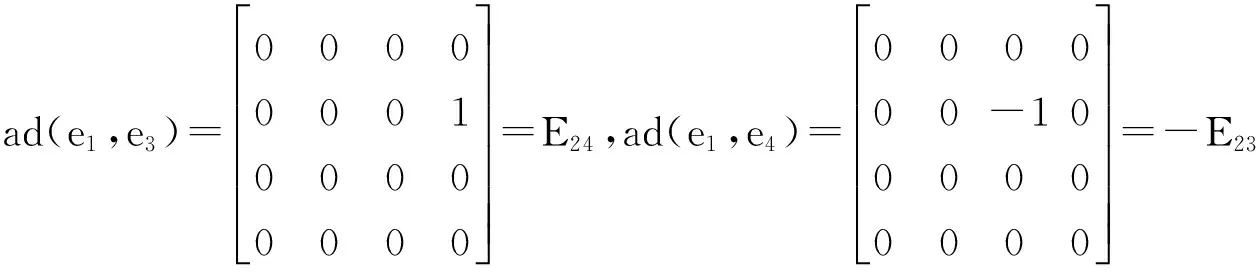
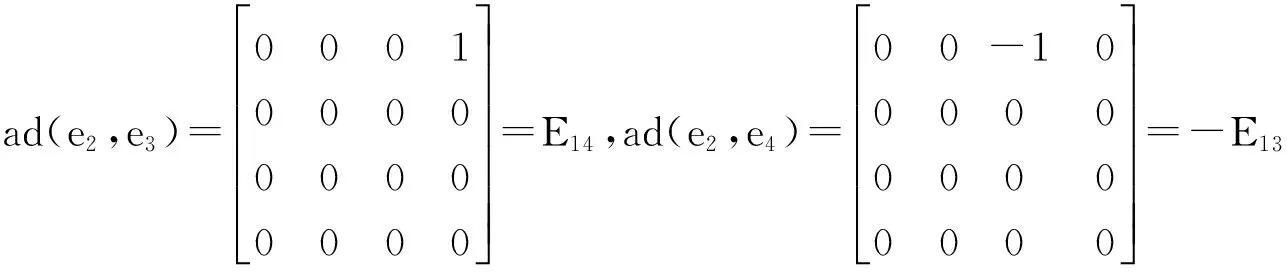
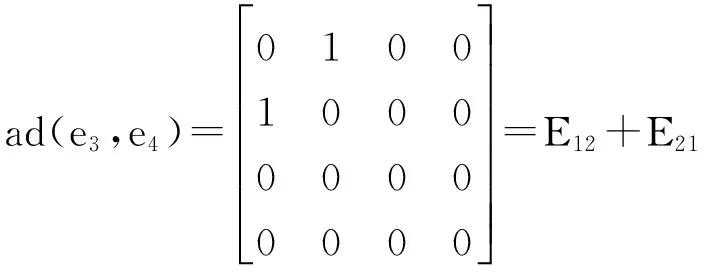
所以任意一个内导子的矩阵为

定理2如果L是Perfect 3-李代数,则ad(L)是李代数TDer(L)的理想.

注:如果L是Perfect3-李代数,那么Der(L)一定不是李代数TDer(L)的理想.在例1中,E11+E22、E33-E44、E12+E21、E13、E14、E23、E24、E34、E43是Der(L)的一组基.而E11、E22、E33-E44、E12、E13、E14、E21、E23、E24、E34、E43是TDer(L)的一组基.

令D1=E11+2E22+E33-E44+E12+E13+E14+E21+E23+E24+E34+E43,D=E11+E22+E33-E44+E12+E21+E13+E14+E23+E24+E34+E43,其中D∈Der(L)，D1∈TDer(L).因为[D1,D]=E21-E12+E23+E24∉Der(L)，所以,[TDer(L)，Der(L)]⊄Der(L),即Der(L)不是李代数TDer(L)的理想.

定理3设L是域F上的Perfect3-李代数,CharF≠5,那么ad(L)在李代数TDer(L)中的中心化子CTDer(L)(ad(L))=0.

证明:令D∈CTDer(L)(ad(L)),对于∀x、y∈L有[D，ad(x,y)]=0.因此,∀x、y、z∈L，D([x,y,z])-[x,y,Dz]=[D,ad(x,y)](z)=0.所以D([x,y,z])=[x,y,Dz].类似的讨论可以得到D([x,y,z])=[x,y,Dz]=[Dx,y,z]=[x,Dy,z],∀x、y、z∈L.对于x1、x2、x3、x4、x5∈L,由定义2得D([x1,x2,[x3,x4,x5]])=[Dx1,x2,[x3,x4,x5]]+[x1,Dx2,[x3,x4,x5]]+[x1,x2,[Dx3,x4,x5]]+[x1,x2,[x3,Dx4,x5]]+[x1,x2,[x3,x4,Dx5]].由于D([x1,x2,[x3,x4,x5]])=[Dx1,x2[x3,x4,x5]]=[x1,Dx2,[x3,x4,x5]]=[x1,x2,[Dx3,x4,x5]]=[x1,x2,[x3,Dx4，x5]]=[x1,x2,[x3,x4,Dx5]].因此,D([x1,x2,[x3,x4,x5]])=5D([x1,x2,[x3,x4,x5]]).由于CharF≠5,所以D([x1,x2,[x3,x4,x5]])=0.因为L是Perfect3-李代数,L的每一个元素都能够表示成[x1,x2,[x3,x4,x5]]的线性组合.所以D=0,即TDer(L)的中心化子CTDer(L)(ad(L))=0.

推论1设L是域F上的Perfect3-李代数,CharF≠5,那么Der(L)在李代数TDer(L)中的中心化子CTDer(L)(Der(L))=0.证毕.

证明:如果CTDer(L)(Der(L))≠0,则存在D∈TDer(L)≠0,使得[D，Der(L)]=0.因为ad(L)⊆Der(L),得到[D,ad(L)]=0,所以CTDer(L)(ad(L))≠0,与定理3矛盾.结论证毕.

3结论

定义了T-导子的概念,通过给出3个定理和1个推论对T-导子代数的结构进行了研究,证明了内导子代数是T-导子代数的理想.在特征不为5的域上Perfect 3-李代数,它的内导子代数及导子代数在T-导子代数的中心化子为零.

参考文献：

[1]FILIPPOV V T.n-Lie algebras[J].Sib Mat Zh,1985,26(6):126-140.DOI:10.1007/BF00969110.

[2]KASYMOV S.On a theory of n-Lie algebras[J].Algebra Logika,1987,26(3):277-297.DOI:10.1007/BF02009328.

[3]NAMBU Y.Generalized Hamiltonian dynamics[J].Phys Rev D,1973(7)：2405-2412.DOI:http://dx.doi.org/10.1103/PhysRevD.7.2405.

[4]TAKHTAJAN L.On foundation of the generalized Nambu mechanics[J].Comm Math Phys,1994,160:295-315.DOI:10.1007/BF02103278.

[5]BAGGER J,LAMBERT N.Gauge symmetry and supersymmetry of multiple M2-branes[J].Phys Rev D,2008,77,065008.DOI:http://dx.doi.org/10.1103/PhysRevD.77.065008.

[6]BAI R P,BAI C M,WANG J X.Realizations of 3-Lie algebras[J].Journal Math Phys,2010,51：063505.DOI:10.1063/1.3436555.

[7]BAI R P,WU Y.Constructions of 3-Lie algebras[J].Linear and Multilinear Algebra,2015,63(11),2171-2186.DOI:10.1080/03081087.2014.986121.

[8]ZHANG Jianhua,WU Baowei,CAO Huaixin.Lie triple derivations of nest algebras[J].Linear Algebra Applications,2005,416:559-567.DOI:10.1016/j.laa.2005.12.003.

[9]ZHOU J H.Triple derivations of perfect Lie algebras[J].Comm Algebra,2013,41:1647-1654.DOI:10.1080/00927872.2011.649224.

[10]白瑞蒲,李奇勇,王伟东,等.素域Fp上的3-李代数[J].河北大学学报(自然科学版),2013,33(5):449-452.DOI:10.3969/j.issn.1000-1565.2013.05.001.

BAI Ruipu,LI Qiyong,WANG Weidong,et al.Structures of 3-Lie algebras over a prime field Fp[J].Journal of Hebei University(Natural Science Edition),2013,33(5):449-452.DOI:10.3969/j.issn.1000-1565.2013.05.001.

[11]白瑞蒲,王伟东,周恒.一类无限维3-李代数的Hom结构[J].黑龙江大学自然科学学报,2014,31(1):26-31.DOI：10.13482/j.issn1001-7011.2014.01.005.

BAI Ruipu,WANG Weidong,ZHOU Heng.Hom-structure of a class of infinite dimensional 3-Lie algebras[J].Journal of Natural Science of Heilongjiang University,2014,31(1):26-31.DOI:10.13482/j.issn1001-7011.2014.01.005.

(责任编辑：王兰英)

T-derivations of perfect 3-Lie algebras

BAI Ruipu,GAO Yansha,ZHANG Yinghua

(College of Mathematics and Information Science,Hebei University,Baoding 071002,China)

Abstract:The T-derivations of 3-Lie algebras,T-derivation Lie algebra TDer(L),and its structure were studied.The relations between TDer(L) and Der(L),ad(L) were discussed.It is proved that the inner derivation algebra ad(L) is an ideal of TDer(L).If L is a perfect 3-Lie algebra over a field F with Char F≠5,centralizers of derivation algebra and inner derivation algebra in TDer(L) are both zero.

Key words:3- Lie algebra；T-derivation；derivation；inner derivation

DOI：10.3969/j.issn.1000-1565.2016.01.002

收稿日期：2015-09-13

基金项目:国家自然科学基金资助项目(11371245)；河北省自然科学基金资助项目(A2014201006)

中图分类号:O175.1

文献标志码：A

文章编号：1000-1565(2016)01-0007-04

第一作者:白瑞蒲(1960—),女,河北保定人,河北大学教授,博士,主要从事李群、李代数研究.

E-mail:bairuipu@hbu.edu.cn