配电网中分布式能源的选址与定容方法

孙博伟(中国电力工程顾问集团有限公司，北京 100120)



配电网中分布式能源的选址与定容方法

孙博伟
(中国电力工程顾问集团有限公司，北京 100120)

摘要：由于能源和环境的双重压力，分布式电源的应用将越来越广泛。在合适的地点安装适当容量的分布式电源能够降低网损，提高电能质量。本文提出了一种分布式电源的选址和定容的方法，改变传统方法的繁琐、使用范围窄的缺点。最后通过MATLAB编写程序对该算法进行了检验，发现该算法程序流程简单，收敛快。

关键词：分布式电源；选址；定容；配电网。

1　概述

分布式电源接入配电网，实现就地消纳，可以提高新能源的利用率、提高电能质量和降低系统网损。然而接入点位置和电源的容量的差异对配电网的影响不同，如果位置和容量不合适，可能会导致系统中某处的电压越限、总系统的网损增加。因此在电源规划阶段分析分布式电源接入点的位置和容量十分有必要。

分布式电源接入点和接入容量的选择问题是一个非线性、多变量、多约束的问题。目前国内外关于这方面的研究主要集中在两个方面，一是数学模型的优化，二是模型求解和算法优化。

已有的诸多研究取决与分布式电源的种类，即是否只向电网提供有功功率。而且很多算法利用准确的损耗公式，计算时需要准确阻抗矩阵和雅可比矩阵，计算效率低。因此针对不同大小、复杂性，有待于找出一种适用于所有情况的方法。本文提出了一种确定分布式电源的最佳容量和位置的分析，该方法计算效率高，适用范围广。

2　模型分析

2.1配网中支路潮流分析

配电网和输电网的不同之处在于，配电网一般都是辐射状，而输电网主要为环网。先以一个典型的辐射状配电网分析网络中的潮流大小。流过支路上的潮流只与支路后面的负载有关。同样，分布式电源接入配电网后，也并非所有线路的潮流大小都发生改变。

一种典型的辐射状配电网见图1，含有一个分布式电源的辐射状配电网见图2。

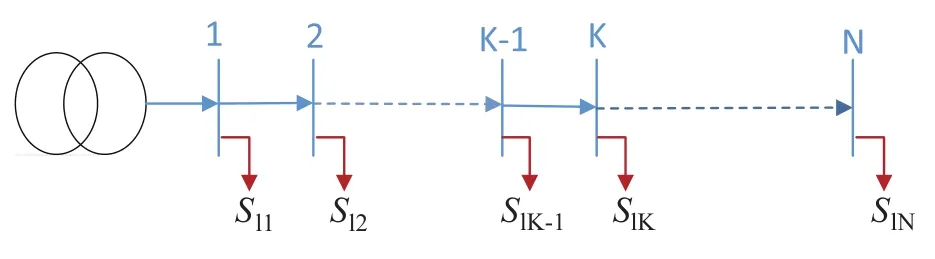
图1　一种典型的辐射状配电网

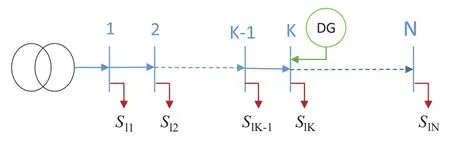
图2　含有一个分布式电源的辐射状配电网

从图1中可以得出流入到节点K的功率：

即电源到节点K之前的节点上的负荷不影响 ，那么SK的表达式可写成：

其中：

当节点K接入分布式电源后，可以等效节点K的负荷变为 。当多个分布式电源接入后，流入节点 的潮流为：

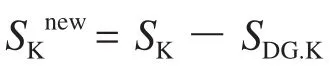
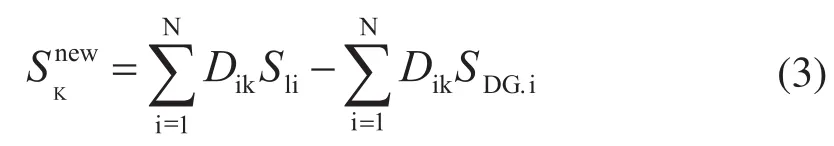
其中，当某个节点没有接入分布式电源时，只需令SDG.K=0即可。

2.2有功无功功率损耗

电流流过电阻就会产生有功损耗。原来系统的有功功率损耗为：

式中： Si=Pi+Qi流入节点i有功和无功； Ui为节点i的电压； Ri为节点 到节点(i - 1)的电阻。

加入分布式电源后，系统的有功功率损耗变为：

通过比较(4)、(5)公式，可以得出分布式电源接入后系统，系统有功损耗减少。为了便于比较，可以定义：

同理可以得出原来系统的无功损耗为：

式中： Li不为节点 到节点(i-1) 的电抗。

接入分布式电源后，系统的无功损耗变为：

通过比较(7)、(8)式，可以得出分布式电源接入后系统，系统无功损耗减少。为了便于比较，可以定义：

那么，系统的有功无功总的减少量，可以建立表达式

式中：λ1、λ2为设定的权重系数，并满足λ1+λ2=1 。根据不同的实际情况，可以设定不同的 λ1、λ2取值，得出理想的结果。例如λ1=1，λ2=1相当于只考虑有功网损。

3　模型求解

通过对上面模型的分析，需要解决的问题是为了获得最大的f，求出分布式电源(DG)的最佳位置与容量。由于分布式电源的功率因数是一个电源本身的属性，为了便于分析与计算，可以取其功率因数为t=cosφ。那么分布式电源的表达式为：

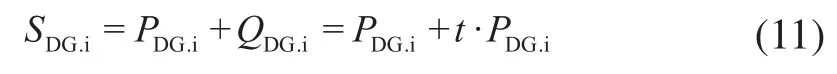
那么，目标函数为：

通过上面的分析可知f是一个关于PDG.i的凸函数，即含有m个分布式电源时， f的海森矩阵正定。

即f一定存在最优解，通过对f求偏导，偏导等于0处必为f的极值，即

当m个分布式电源的位置确定时，可以通过公式(14)求出每个分布式电源的有功功率，然后通过式(11)可以得出分布式电源的容量。

一旦分布式电源的位置确定，它的最佳容量可以利用上面方法进行求解。关于分布式电源位置的选择，采用以下计算步骤。

(1)当m=1。我们根据式(13)可以求出每个节点分布式电源的最佳容量，取f的最大值点作为第一个分布式电源的位置，该点的最佳容量就为分布式电源容量。

(2)当已经确定k个分布式电源的容量和位置，求第k+1个分布式电源的位置时。首先将含分布式电源k个节点负荷等效为Sli=Sli- SDG.i。接着按照第一步求解m=1时的位置，而这个位置就是第k+1个分布式电源的位置。

(3)求出k+1个分布式电源的容量后，令m=k+1利用公式(13)可以计算出每个位置的最佳容量。

4　算例分析

为了验证本文提供算法的正确性，采用MATLAB语言编写分布式电源选址和定容程序，配网参数采用IEEE33节点配电网系统，见图3，分布式电源的数量为3。其中分布式电源的功率因数等于总负荷的功率因数0.85。权重系数λ1=1，λ2=1。

图3　IEEE33节点配电网

通过计算，分布式电源的位置分别是节点5、节点24、节点30。各个节点的容量见表1。

表1　最佳补偿节点与位置

加入分布式电源后，系统的有功网损从360.55 kW，下降到43.01 kW。每次加入分布式电源后，网络中个节点的电压都会发生变化，具体变化见图4。

图4　加入分布式电源前后的系统各节点电压

通过观察图4发现，第一个分布式电源加入后系统电压改善最为明显，而实际第一个分布式电源加入后，系统网损改变的也最多。分布式电源加入越多，系统电压增加越多，当大量分布式电源接入时，可能会导致系统电压越限，因此计算时还必须要考虑电压约束。若发生电压越限时，必须降低分布式电源的无功出力。无论何种优化，都是在保证电力系统在安全的前提下进行的。

5　结论

本文提出了一种配电网中分布式电源选址和定容的分析方法，并通过MATLAB编写程序验证了该算法的正确性。通过研究发现该算法收敛快，计算程序简单，特别适合实际工程上应用。

算例中只是简单增加了3个节点，当多个节点加入时，模型就会变得复杂，那么更多的需要考虑电压在安全范围内。本文提供的算法只能得到一个较优解，而不能得到最优解，需要更深入的挖掘模型，才能得到更为精确的解。

参考文献：

[1]杨琦，张建华．风光混合供电系统多目标优化设计[J]．江苏电机工程，2005，24(2)．

[2]W.EI-Khattam，Y.G.Hegazy，M.M.A.Salama．An integrated distributed generation optimization model for distribution system planning[J]．IEEE Transactions on Power Systems，2005，20(2)．

[3]胡骤，吴汕头，夏翔．考虑电压调整约束的多个分布式电源准入功率计算[J]．中国电机工程学报，26(19)．

[4]徐讯，等．考虑环境成本和时序特性的微网多类型分布式电源选址定容规划[J]．电网技术，2013，37(4)．

[5]郑漳华，等．考虑环境因素的分布式发电多目标优化配置[J]．中国电机工程学报，2009，29(13)．

[6]顾承红，艾芊．配电网中分布式电源最优布置[J]．上海交通大学学报，2007，41(11)．

[7]麻秀范，崔换君．改进遗传算法在含分布式电源的配电网规划中的应用[J]．电工技术学报，2011，26(3)．

[8]郑睿，吴红斌．基于遗传算法的配电网中分布式电源选型与选址[J]．合肥工业大学学报，2012，35(3)．

[9]杨宝杰，海晓涛．基于量子粒子群算法的配电网分布式电源选址和定容[J]．陕西电力，2010，24(12)．

[10]刘波，张焰，杨娜．改进的粒子群优化算法在分布式电源选址和定容中的应用[J]．电工技术学报，2008，23(2)．

[11]汪兴旺，邱晓燕．基于改进粒子群算法的配电网分布式电源规划[J]．电力系统保护与控制，2009，37(14)．

[12]Falaghi H，Haghifam M．ACO based algorithm for Distributed Generation Sources Allocation and Sizing in Distrib Ution Systems[C]//Power Tech 2007 IEEE Lausanne，2007．

[13]王成山，等．配电网扩展规划中分布式电源的选址和定容[J]．电力系统及其自动化，2006，30(3)．

[14]马溪原，等．采用改进细菌觅食算法的风/光 /储混合微电网电源优化配置[J]．中国电机工程学报，2011，31(25)．

Aanalytical Method of Optimal Siting and Capacity for Distributed Generation in Distribution Network

SUN Bo-wei
(China Power Engineering Consulting Group Co., Ltd., Beijing 100120, China)

Abstract:Due to the double pressure of energy and the environment, the application of distributed power supply will be more and more widely. In a suitable location to install the appropriate capacity of distributed power supply can be able to decrease network loss, and improve power quality. This paper proposes a distributed power capacity and location volume method, the site selection of change of the traditional methods, using a narrow range of faults. Finally has carried on the inspection to the algorithm by MATLAB program, found that the algorithm program process simple, convergence is fast.

Keywords:distributed generation; optimal location; optimal capacity; distribution network.

中图分类号：TM72

文献标志码：B

文章编号：1671-9913(2016)01-0061-04

* 收稿日期：2015-06-09

作者简介：孙博伟(1983- )，男，河北深泽人，工程师，主要从事企业发展战略研究。