基于姿态分析的自导引小车控制器的设计
董玉德+陈光超+杨先龙+王桂英+张剑锋
摘 要:通过对自导引小车(Automated Guide Vehicle,AGV)的国内外市场以及技术现状的分析,设计了适用于工厂车间的低成本AGV。运用ATmega128单片机设计了基于姿态研究的AGV模糊控制器,采用模糊控制算法对AGV两轮差速转向进行控制,提出了基于姿态分析对小车行驶状态进行优化,并进行了不同道路的运动试验。试验表明,加入了姿态分析的模糊控制器能够对小车的某些特殊运行点的姿态进行预判断,并在AGV行驶过程中更为有效地保证小车运行姿态,同时减小小车运行时产生的超调,使小车更为准确地追踪导引路径。
关键词:自动导引小车;姿态分析;模糊控制;分析试验
中图分类号: TP273+.4文献标文献标识码:A文献标DOI:10.3969/j.issn.2095-1469.2016.03.03
Abstract:Through the analysis of the domestic and foreign markets and technology status of automated guide vehicle (AGV) systems, a low-cost automated guide vehicle was designed for factory floor. In this paper, the ATmaga128 was used to design a fuzzy controller for the AGV based on posture analysis. The fuzzy controller algorithm was put forward to control the two-wheel difference speed steering AGV, the driving state was optimized based on posture analysis and the AGV had been tested on different roads. The results show that the fuzzy controller with posture analysis can pre-judge the driving posture of AGV at some special points. Meanwhile, the driving posture of AGV can be controlled more effectively, and the overshoot of AGV in the running process can be reduced, which keeps AGV following the guiding line more accurately.
Keywords:automated guided vehicle; posture analysis; fuzzy controller; analysis test
近几年,随着我国工业领域中柔性制造及装配系统的应用逐步增多,AGV也越来越受到各行业的重视[1]。但我国的AGV发展起步较晚,技术普遍落后于欧美国家,产品更新较慢,核心竞争力较小,且大量的关键技术被欧美企业掌控,在中国发展中低端的AGV产品更具市场竞争力。该种产品不要求功能强大,只需满足正常的搬运要求即可[2]。因此,如何有效控制AGV的搬送、运行便成为发展该类产品的核心问题[3]。目前,我国研究AGV技术的高校众多,但多以先进的AGV技术研究为主,只有极少数涉及这种低成本AGV研究。
针对更符合中国市场的低成本AGV进行分析研究,同时依托某企业的实际项目进行了产品的研发设计与试验。结合模糊控制理论与特殊姿态分析方法对AGV模糊控制器进行设计与优化。该AGV样机采用磁条导航,通过差速转向方式运行。文中的试验数据及结果均依靠该样机获得。
1 AGV模糊控制器设计
1.1 智能车控制系统组成
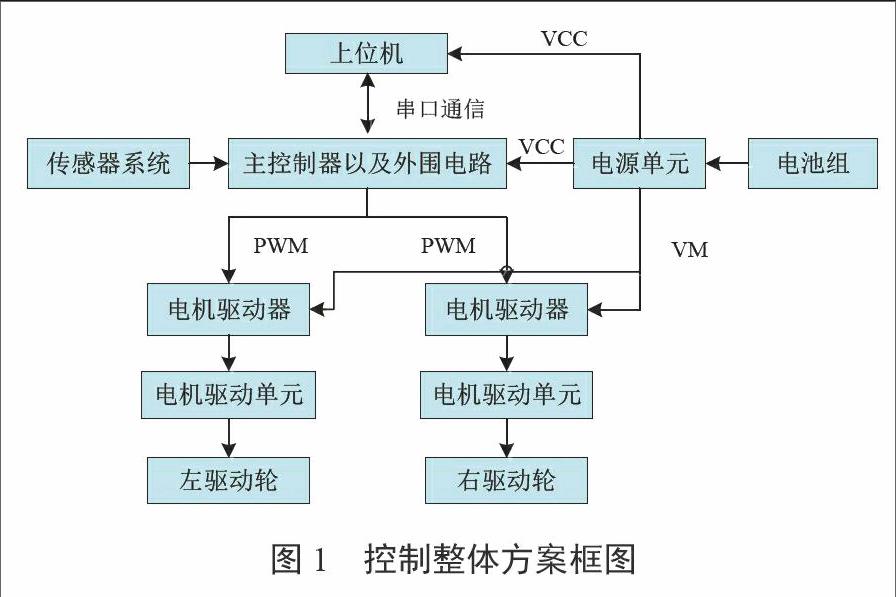
AGV的控制系统大体由路径识别系统、速度控制系统和主控系统三部分组成。路径识别系统是AGV的“眼睛”,它能准确告知小车行驶的位置。速度控制系统包括速度检测系统和电机驱动系统两部分。主控系统是智能车的核心,由单片机及外围电路等硬件组成。
本次设计中,路径识别系统采用磁导航传感器读取磁条来反映小车的行驶位置以及偏移状态,所用的磁条导航传感器有8路检测点以及8路数字信号输出端口。主控制单元通过对磁导航传感器所得到的信息进行分析,得到小车的偏移位置及速度控制系统的电机控制量,从而达到对智能车准确控制的目的。样机的速度控制系统采用的是直流无刷电机和D型驱动器,分别控制样机左右两轮的速度。图1是智能车的控制整体方案图。
1.2 智能车模糊控制器设计
1.2.1 模糊控制器参数设置
模糊控制器的设计包含:输入、输出参数的模糊化、模糊规则库的建立、模糊推理以及输出参数的去模糊,因此构建模糊控制器,首先需要建立控制模型,确定输入、输出参数[4]。项目设计的模糊控制器设置输入参数为磁导航传感器传入的偏差e,以及偏差变化率Δe,输出参数为左、右电机调速信号PWM波的占空比差值u。其中,偏差变化率Δe定义为上次偏差的论域绝对值减去本次偏差的论域绝对值,即Δe =|Elast_time|-|Ethis_time|。
模糊控制器对传感器所得到的信号进行分析以及编码,使其形成模糊量,进而参加模糊推理。磁条导航传感器传入的8位数字信号,设其8位输出信号从左至右依次为L7到L0,表明了小车相对磁条的偏差量。由于偏差信号不连续,也不呈现单调递增规律,因此设置编码值。其编码表见表1。
设偏差值的模糊量为E,偏差变化率的模糊值为EC,U为速度的变化控制量。经试验后分析,设偏差e的基本论域为[-4,4],偏差变化率Δe的基本论域为[-1, 0],控制量u的基本论域为[-4,4]。
e和u的模糊集分别取7个语言值,分别为:
{负大,负中,负小,0,正小,正中,正大}即{NB,NM,NS,ZO,PS,PM,PB }。
Δe的模糊集取3个语言值,分别为:
{负大,0,正大}即{ NB,ZO,PB }
上文中:u表示左、右调速PWM波占空比差值,规定:当U>0时,左电机PWM波信号的占空比大,说明智能车要向左转;当U<0时,右电机PWM波信号的占空比大,说明智能车要向右转。
由于模糊控制器需要的是模糊量,而传感器所检测到的是精确量,故需要将精确量模糊化。偏差e和输出量u采用三角隶属度函数进行模糊化,如图2所示[5]。而对于偏差变化率Δe的模糊化采用单值模糊化的方法,即:EC为-1,对应于增大(PB);EC为0,对应于无变化(ZO);EC为1,对应于减小(NB)[6]。
1.2.2 模糊推理与解模糊
在智能车控制系统中,对于一个双输入单输出的模糊控制器,其控制规则通常采用以下的模糊条件语句,即:
If E and EC then U。
其中:E、EC分别为输入系统偏差量e和偏差变化率Δe模糊化的模糊集合。通过对路径的分析,根据开车的经验得到相应的模糊控制规则见表2。
AGV模糊控制规则库的建立应满足:当偏差较大时,左、右电机转速差应较大,使小车能够迅速减小偏差;当偏差较小时,在使小车减小该偏差的同时,应尽量避免过大超调量的出现,以免引入反向偏差[7]。
解模糊方法采用重心法,对于论域离散情况,该方法可表示为式(1)[8]。
1.3 基于Simulink的模糊控制仿真
建立模糊控制器模型后,利用Matlab中Fuzzy工具箱对该模糊控制器进行仿真分析。通过模糊控制规则在工具箱中建立模糊推理系统编辑器以及隶属度函数曲线,然后建立Simulink模型,进行系统测试和仿真,得到系统整定结果和响应曲线,如
图4所示。根据响应曲线得知系统响应快,抗干扰能力强。
2 基于姿态分析对控制器进行优化
2.1 姿态分析的原理
姿态分析是对AGV运行过程中车体运行方向中心线与磁条之间的角度偏差的分析,如图5所示。直线运行时,偏差角度为车体中心线与磁条的夹角;弯道运行时,偏差角度为车体中心线与磁条切线的夹角。
对于进行精确角度偏差的定量分析,至少需要两个磁条导航传感器[9]。通过置于车体前后两端的传感器所读取的偏差值,可计算出小车相对于磁条的准确角度偏差。本次设计只有一个磁条传感器,无法做到精确定量分析,依靠AGV运动学模型对角度偏差分析进行简化,从而实现姿态的初步矫正。AGV运动学模型如图6所示。图中,vl、vr 分别为左、右驱动轮速度,m/min;L为驱动轮之间距离,m;R为AGV的旋转半径,m。
根据运动学模型,可得到AGV运行速度表达式:
分析运动学模型和式(3)可知:小车的实际运行过程为直线与圆弧的结合。同时,小车的偏差矫正实际为利用圆弧段对直线磁道以及圆弧磁道进行插补。
2.2 直道运行的姿态优化
直道运行时的偏差矫正是利用圆弧对直线进行插补,因此,在矫正偏差的同时姿态也会发生变化。
在进行模糊控制设计时,直道运行须在6个检测点(8个检测点中除去最外侧2个点)内完成。因此偏差为NS或PS,且偏差变化率为NB这两点为姿态矫正点,如表2浅灰色区域所示。
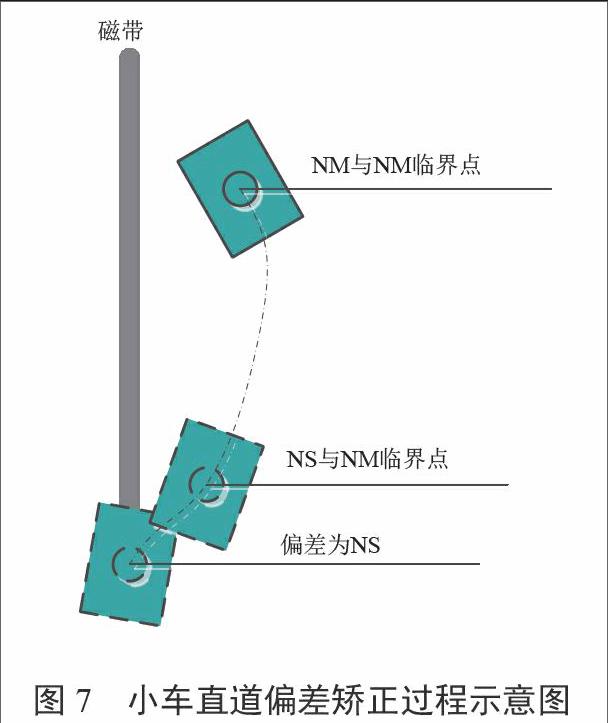
当小车由偏差为NS位置运行到NM位置或由PS位置运行到PM位置时,小车运行方向沿着偏离磁道的方向;当用式(3)所表示的圆弧进行姿态矫正时,矫正轨迹为圆弧线,在矫正过程中小车最初离磁道距离会增大,而后才逐渐减小。以偏差由NS(右稍偏)到NM(右中偏),矫正由NM位置到NS位置为例,小车直道偏差矫正过程示意图如图7所示。
图7中,NS与NM临界点到NM与NS临界点为小车偏差矫正阶段,矫正结束时,小车与磁条产生较大角度差,形成了不良姿态。
由式(2)可知,如果小车在转弯时,左、右驱动轮转速满足式(4)~(6)的要求,则小车直线与圆弧运动时的运行速度均为v不变。假设vl>vr,则:
为改善这一不良姿态,可利用与偏差矫正圆弧方向相反的另一圆弧进行姿态矫正。姿态矫正过程不仅使小车姿态得到改善,同时使小车进一步逼近磁条。姿态矫正过程如图8所示。
由于驱动轮的速度与其电机的PWM波占空比成正比,设小车设置速度v所对应的基本PWM占空比为Dbase,左、右电机PWM波占空比差值为ΔD,则式(7)可转换为:
由式(8)可知,只要给定合适的ΔD就能使小车形成反向姿态矫正圆弧。ΔD的值与L和Dbase均有关,在实际设计过程中,固定小车左、右驱动轮之间的距离,通过Dbase来选取合适的ΔD,同时设定矫正时间为1 s。ΔD要设置合适的值,使小车姿态矫正结束点落在ZO或NS(PS)区域,以免产生不必要的超调[10]。在本设计中,为使姿态矫正效果观测明显,L取较大值固定为80 cm。用ΔDz表示直道姿态矫正占空比差值,其参数设置为:
(1)当Dbase30/25511.76%时,v7.39 m/min,ΔDz 13/2555.10%。
(2)当Dbase40/25515.69%时,v9.85 m/min,ΔDz 17/2556.67%。
(3)当Dbase50/25519.61%时,v12.31 m/min,ΔDz 21/2558.24%。
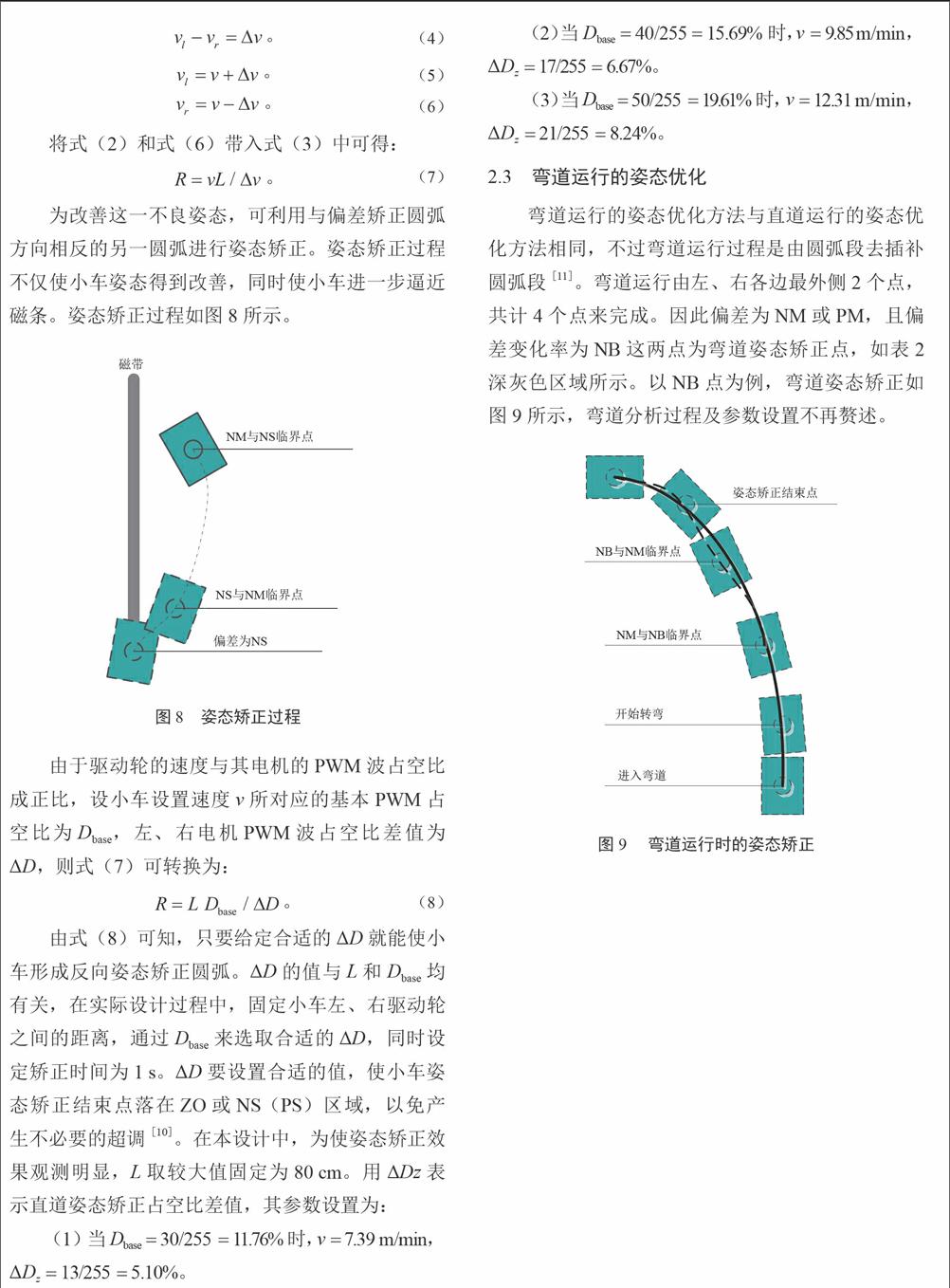
2.3 弯道运行的姿态优化
弯道运行的姿态优化方法与直道运行的姿态优化方法相同,不过弯道运行过程是由圆弧段去插补圆弧段[11]。弯道运行由左、右各边最外侧2个点,共计4个点来完成。因此偏差为NM或PM,且偏差变化率为NB这两点为弯道姿态矫正点,如表2深灰色区域所示。以NB点为例,弯道姿态矫正如图9所示,弯道分析过程及参数设置不再赘述。
2.4 姿态优化过程
本次设计中的姿态优化采用的是“定值”方法,即姿态矫正所需的反向矫正圆弧的半径以及矫正时间均固定,因此矫正过程中的偏差可能会呈现一种振荡衰减的趋势[12]。试验中发现:姿态、偏差矫正过程中一般振荡次数为1~3次,而后小车姿态回归到较为理想的状态。
以直道运行为例,这一现象产生的原因如图10所示。
偏差矫正轨迹与小车的车体中心线相切,由图10可知:3条轨迹线所对应的小车在NS与NM临界点处的姿态角不相同,从而导致其在NM与NS临界点处的姿态角也不同。若用相同半径的矫正圆弧以及相同的矫正时间来对不同初始姿态角的小车进行姿态矫正,必然会出现偏差的振荡现象。该振荡现象说明,进行姿态矫正时,出现了给予矫正量富余以及给予矫正量不足的情况,因此可能需要进行1~3次正常矫正才能使小车达到满意姿态。对于此次设计的低成本方案,这种现象较难避免,但对于正常使用基本无影响。
3 试验
3.1 试验样机
样机的驱动系统结构如图11所示。
电机与驱动系统之间通过5M600型号的同步带相连,可实现正反转,同时其减振作用可利于小车紧急停车时减小冲击力[13]。驱动轮选择26.7cm的铸铁芯橡胶轮,电机选用某公司型号为FBL-92H25301RS的无刷直流电机,该电机额定转矩0.8 N·m,额定转速3 000 r/min。减速机选用减速比为1∶30的斜齿轮减速机,型号为6GU-30K。
AGV的车架选用10号以及5号槽钢焊接而成,如图12所示。
3.2 试验准备
试验中磁条选用宽30 mm,厚1.2 mm的N极磁条,磁条导航传感器与磁条距离为20±5 mm。同时,试验地面为水磨石地面,与橡胶轮的滚动摩擦因数为0.015~0.020,满足试验要求。试验中小车承载重量为1人重量,约60 kg。
试验中利用秒表对小车在规定长度或规定半径的90°弯道上的行驶时间进行计时,通过计数时间可计算出小车实际运行速度,将实际运行速度与设置速度进行比较,即能知道小车运行姿态如何。原因在于,若小车实际运行速度远小于设置速度,则可知小车运行过程中姿态不好,“蛇形”运行过多,导致小车实际运行距离增大,从而运行平均速度降低。
3.3 试验方案及结果
试验分为直道试验与弯道试验。本次试验为了更好地观测小车姿态矫正效果,将驱动轮之间的距离L固定为较大值,同时降低小车的设置速度,使小车转弯半径值R增大,姿态矫正过程更为具体、直观。
3.3.1 直道试验
直道试验截取8 m长磁条作为导引路径,以不同设置速度分成两组并进行6次试验。求取每组试验平均速度以后,将试验平均速度与设置速度相比较,同时计算出每组试验平均速度所对应的相对误差限。
直道试验方案及数据见表3。根据表3中数据可知,样车每组直道运行测得的平均速度相对误差限均在10%以内,在设置速度较低时相对误差限可保证在5%以内。同时相同设置速度下的每次试验,所测得的实际速度相差不大,小车的运行姿态保证较好。
3.3.2 弯道试验
弯道试验的试验方法与直道试验相同。弯道试验以规定半径的90°弯道作为导引路径,其试验方案和平均数据见表4。表4中的行驶时间、实际速度和相对误差限均为平均值。
弯道试验中各组试验的相对误差限均在15%以内,当速度较低时相对误差限可保证在8%以内。同时观测小车运行过程中驶入弯道时超调量最大,而随着小车继续行驶,超调量逐步减小,因此小车弯道运行时的姿态也保证较好。试验中弯道最小半径可达1.5 m。
4 结论
(1)对低成本AGV控制器的研究提出了一种快速、简便的优化方法,通过分析AGV运行姿态,并结合模糊控制理论,设计并优化了传统的AGV模糊控制器。
(2)本文对AGV样机进行了设计,并对该控制器进行了实际试验。试验中,为观测小车姿态矫正效果,对样机和试验方案进行处理,处理方案包括将设计驱动轮距L固定为较大值,并降低小车的设置速度,同时将测试距离和测试弯道角度的值都设为固定值等。
(3)试验表明,基于姿态分析的模糊控制器能够有效保证AGV在直道和弯道上的运行姿态,同时提高了AGV的运行精度,减小了运行时产生的超调。
参考文献(References):
张辰贝西,黄志球.自动导航车(AGV)发展综述[J].中国制造业信息化,2010,39(1):53-59.
ZHANG Chenbeixi,HUANG Zhiqiu.Evolution summari-zation of Automatic Guided Vehicle (AGV) [J]. Manu-facture Information Engineering of China,2010,39(1):53-59. (in Chinese)
ANGELOUDIS P,BELL M G H. An Uncertainty-Aware AGV Assignment Algorithm for Auotoumated Container Terminals [J]. Transportation Research Part E:Logistics and Transportation Review,2010,46(3):354-366.
武星,楼佩煌,唐敦兵. 自动导引车路径跟踪和伺服控制的混合运动控制 [J]. 机械工程学报,2011,47(3):43-48.
WU Xing,LOU Peihuang,TANG Dunbing. Integrated Motion Control of Path Trcaking and Servo Control for an Automated Guided Vehicle [J]. Chinese Journal of Mechanical Engineering,2011,47(3):43-48. (in Chinese)
GELAREH S,MERZOUKI R,MCGINLY K,et al. Scheduling of Intelligent and Autonomous Vehicles Under Pairing/Unpairing Collaboration Strategy in Container Terminals [J]. Transportation Research Part C:Emerging Technologies,2013,33:1-21.
汪木兰,顾绳谷. 模糊控制的发展、困惑和趋势[J].电气自动化,1994(1):9-11.
WANG Mulan,GU Shenggu. The Development,Perp-lexity and Trend of fuzzing control [J]. Electrical Auto-mation Magazine,1994(1):9-11. (in Chinese)
陈永义,陈怡欣. 从工程应用看模糊逻辑控制[J]. 控制系统与数学,1999,13(2):33-36.
CHEN Yongyi,CHEN Yixin. Comments on Fuzzy Logic Control from the Viewpoint of Engineering Application [J]. Fuzzy Systems and Mathematics,1999, 13(2): 33-36. (in Chinese)
张晓军,张二为.智能控制系统发展综述及其应用[J].有色冶金设计与研究,2006,27(1):8-12.
ZHANG Xiaojun,ZHANG Erwei. An Overview to the Intelligent Control System Development and Its Application [J]. Nonferrous Metals Engineering & Research,2006, 27(1):8-12. (in Chinese)
魏权利,李丽萍,于竹林. 模糊神经网络在嵌入式移动机器人避障中的应用研究[J]. 机床与液压,2010, 38(17):51-54.
WEI Quanli,LI Liping,YU Zhulin. Application of Fuzzy Neural Network in Embedded Movable Robot Avoiding Obstacle System [J]. Machine Tool & Hydraulics,2010,38(17):51-54. (in Chinese)
DOUDOU S,KHABER F. Direct Adaptive Fuzzy Control of a Class of MIMO Non-affine Nonlinear Systems [J]. International Journal of Systems Science,2012,43(6):1029-1038.
吴伟涛,刘文波. 磁引导式差速转向AGV的电机确定与磁导航方法 [J].机电信息,2012(36):144-145.
WU Weitao,LIU Wenbo. Motor to Determine and the Magnetic Navigation Method for Magnetic Guided Differential Steering of AGV [J]. Mechanical and Electrical Information,2012(36):144-145. (in Chinese)
陈无畏,孙海涛,李碧春,等. 基于标示线导航的自动导引车跟踪控制[J]. 机械工程学报,2006,42(8):164-170.
CHEN Wuwei,SUN Haitao, LI Bichun,et al. Tracking Control of Automatic Guided Vehicle Based on Lane Marker Navigation [J]. Chinese Journal of Mechanical Engineering,2006,42(8):164-170. (in Chinese)
张轲,吴毅雄,吕学勤,等. 差速驱动式移动焊接机器人动力学建模 [J]. 机械工程学报,2008,44(11):116-120.
ZHANG Ke,WU Yixiong,LYU Xueqin,et al . Dynamic Modeling for Differentially Steered Welding Mobile Robot [J]. Chinese Journal of Mechanical Engineering,2008, 44(11):116-120. (in Chinese)
卢小锐,高文志,张良良,等. 基于Excite-Timing Drive的正时同步带系统动力学分析[J].振动与冲击,2013,32(11):66-69.
LU Xiaorui,GAO Wenzhi,ZHANG Liangliang,et al. Dynamic Analysis of a Synchronous Belt Drive Based on Excite-TD [J]. Journal of Vibration and Shock,2013, 32(11):66-69. (in Chinese)

