广义质量替代的曲柄群机构动平衡

刘言松, 曹巨江

(陕西科技大学 机电工程学院， 陕西 西安　710021)



广义质量替代的曲柄群机构动平衡

刘言松, 曹巨江

(陕西科技大学 机电工程学院， 陕西 西安710021)

摘要：根据曲柄群机构中连杆桁架的质心分布特点，利用广义质量替代法将连杆桁架质量向曲柄与连杆桁架的3个铰接点替代，从而将曲柄群机构分解为若干个I类和II类曲柄单元，把曲柄群机构的动平衡问题转化为I类曲柄单元的动平衡问题.计算表明.当I类曲柄单元实现动平衡时，曲柄群机构也实现了动平衡.结论对简化曲柄群机构的结构，减少该机构的基础振动具有较好的指导意义.

关键词：曲柄群机构； 广义质量替代； 曲柄单元； 动平衡

0引言

曲柄群机构在专用钻床[1]、卷烟机械中的包装设备、印刷机械等需要实现平行轴同步传动的等场合应用较为广泛[2-4].曲柄群机构示意图如图1所示.

图1中，所有曲柄均具有相同的长度和运动相位，任意两个曲柄间均构成一个平行四边形机构[5-7]，因此主动曲柄和从动曲柄具有相同的运动状态，所有连杆也具有一致的运动状态，因此所有连杆实际上构成了一个桁架杆.在实际生产中，为了减少连杆桁架的质量，连杆桁架一般都采用轻质材料及图1所示的杆结构.但是根据连杆桁架的运动特点，其对回转轴的惯性力难以消除，由此引起的机构振动不可避免[8].文献[3,9]只对曲柄群机构在机构所在平面的平衡进行了初步研究，并没有涉及到该机构的动平衡问题.在曲柄群的实际应用中，连杆桁架和曲柄所在平面并不共面，如图2所示，其中L2为曲柄和连杆桁架的轴向距离.

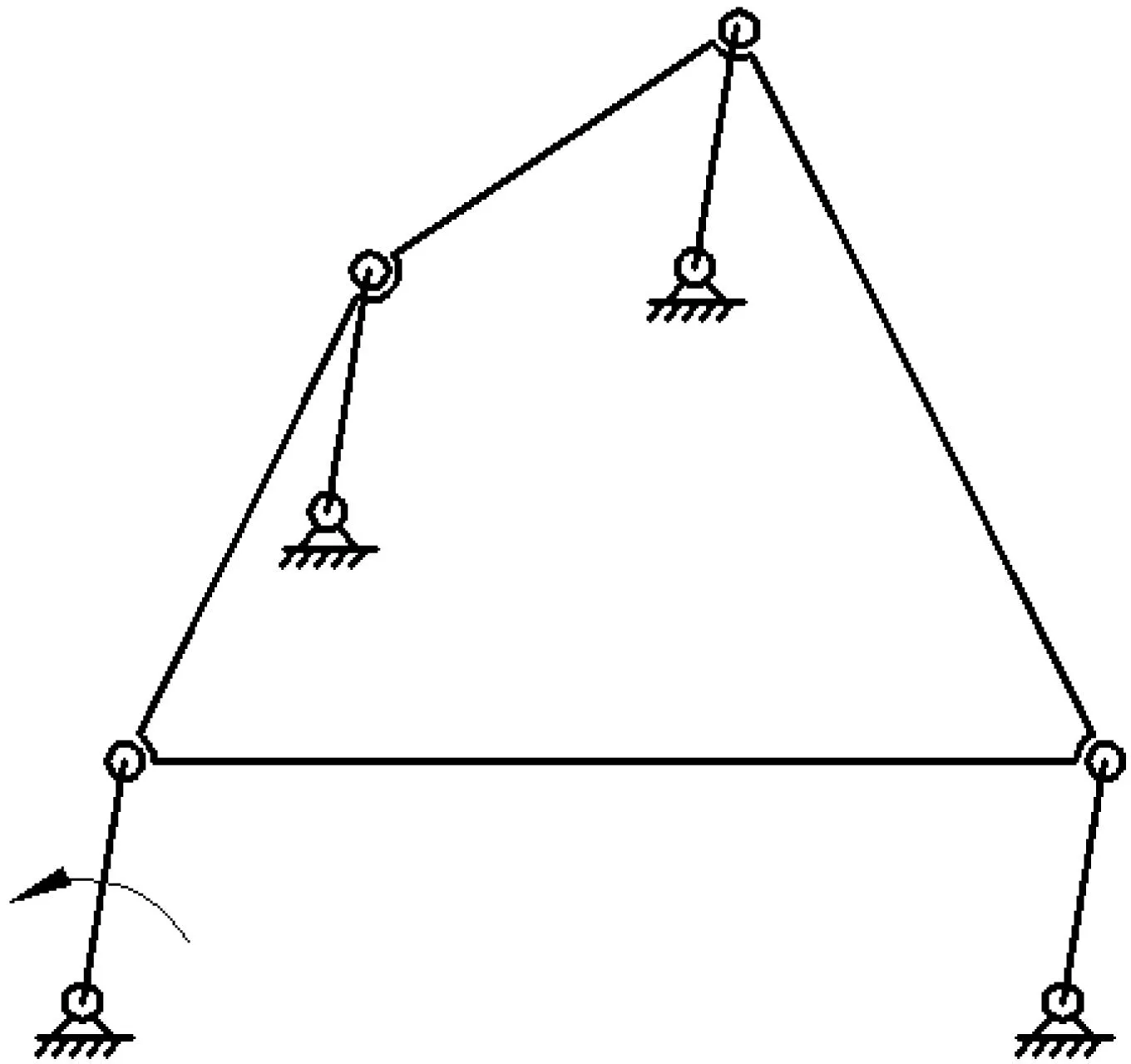
图1　曲柄群机构示意

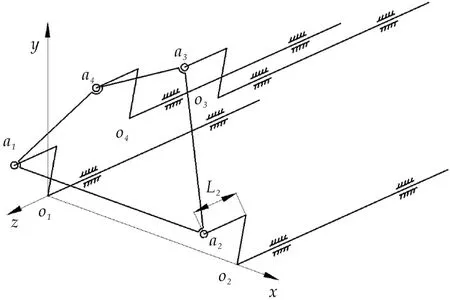
图2　曲柄群机构空间分布示意图

曲柄和连杆桁架质量引起的惯性力虽然可以通过很多方法进行静平衡，但是惯性力引起的力矩并不能有效消除.本文通过利用广义质量替代法把连杆桁架的质量向曲柄与连杆桁架的铰接点替代，将曲柄群机构分解为结构类似的两类曲柄单元，推导第I类曲柄单元的动平衡时曲柄及配重的质径积与分布相位角公式，得到曲柄单元动平衡的理论与方法，以此得出曲柄群机构动平衡的条件，最后以一个算例验证了本方法的正确性.

1连杆桁架的广义质量替代

图3为曲柄群机构的连杆桁架示意图，a1、a2、a3、a4点为连杆桁架与曲柄的铰接点.对于曲柄回转中心任意分布的曲柄群，均可以建立图3所示的坐标系，其中(xs,ys)是连杆桁架质心在坐标系ξa1η中的坐标.

将连杆桁架质量m向任意多个铰接点进行质量静替代时，需满足关系式(1)[10]：

其中，(xai,yai)为连杆桁架铰接点在坐标系ξa1η中的坐标，mai为铰接点ai处的替代质量，n为替代的铰接点数.对于式(1)，仅当n=3时有实数域的确定解，因此可以将连杆桁架的质量向任意3个铰接点进行替代，得到式(2)：

(1)

(2)

解式(2)即可得出连杆桁架向铰接点a1、a2、a3的替代质量.

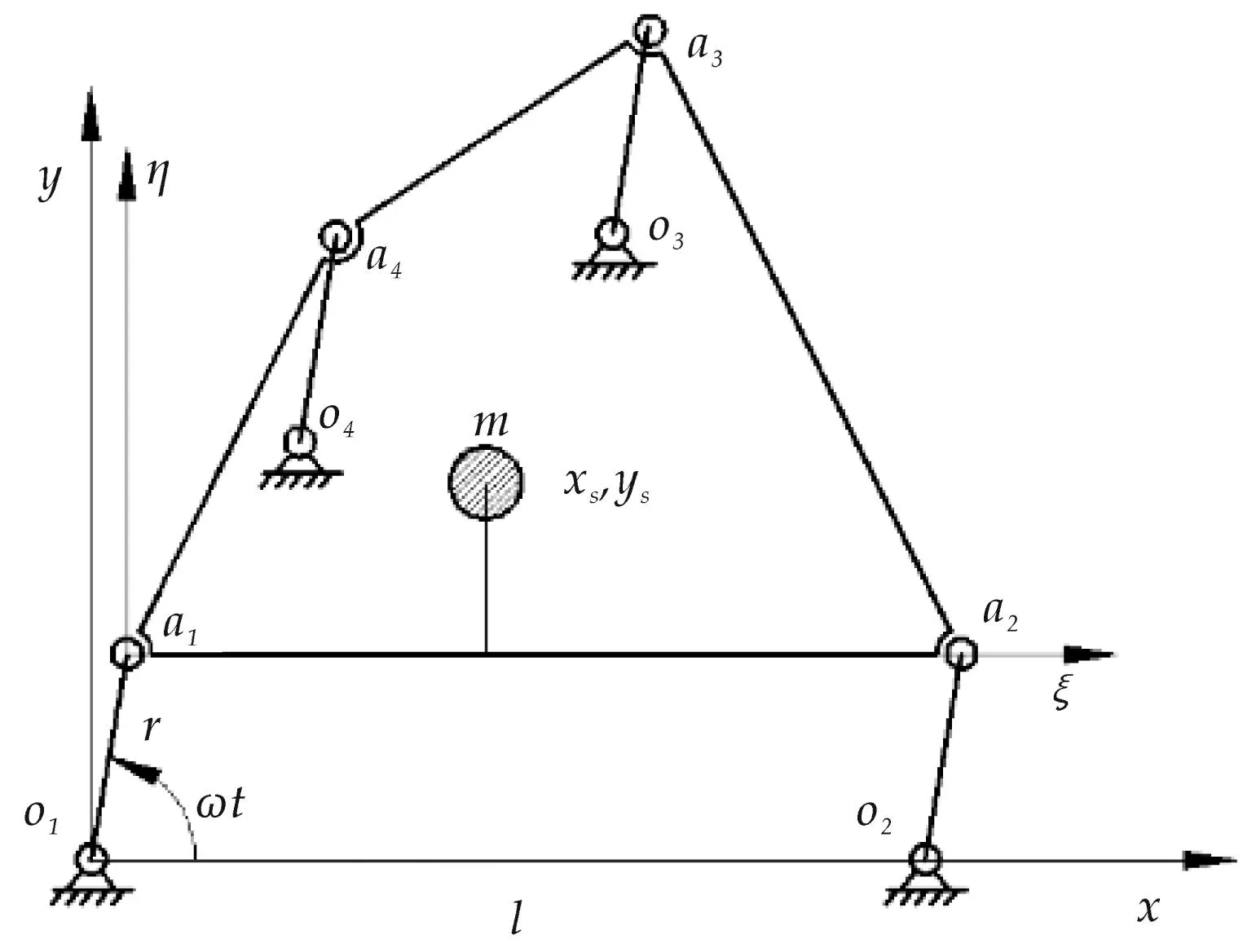
图3　连杆桁架

完成广义质量静替代的曲柄群可以分解为两类以曲柄为核心的曲柄单元.第I类曲柄单元为曲柄与连杆桁架铰接点有替代质量的曲柄单元，如图3中的分别以曲柄o1a1、o2a2和o3a3为核心的曲柄单元即为I类曲柄单元.第II类曲柄单元是曲柄与连杆桁架铰接点处没有替代质量的曲柄单元，如图3中的以曲柄o4a4为核心的曲柄单元即为II类曲柄单元.对于第II类曲柄单元，可以将曲柄的质心设计在其回转中心处，因此该类曲柄单元不产生惯性力，不需要进行动平衡.I类曲柄单元组含有广义替代质量，必须对其进行动平衡.

2I类曲柄单元的动平衡

根据前述分析，如果将桁架的质量向3个铰接点进行广义质量替代，曲柄群机构的动平衡问题就转化为I类曲柄单元的动平衡问题.I类曲柄单元的空间布局简图如图4所示.

鉴于曲柄群机构的空间分布特点，由于连杆桁架必须分布于轴端，因此选择轴的另一端为配重面T′.从简化结构考虑，将曲柄视为配重，即选择曲柄所在平面为配重面T″，由图4可得到图5所示的连杆桁架质量向配重面T′和T″替换的示意图.

将式(1)表示的铰接点a1、a2和a3的广义质量向T′和T″两个配重平面进行替代得[11]：

(3)

替代质量在T′、T″面的相位角分别为

(4)

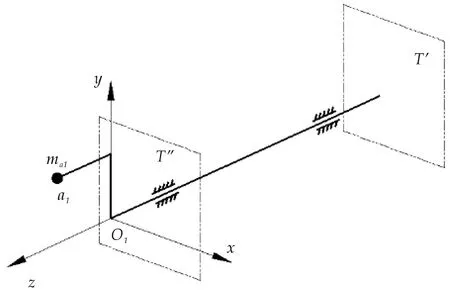
图4　Ⅰ类曲柄单元o1a1的空间布局简图

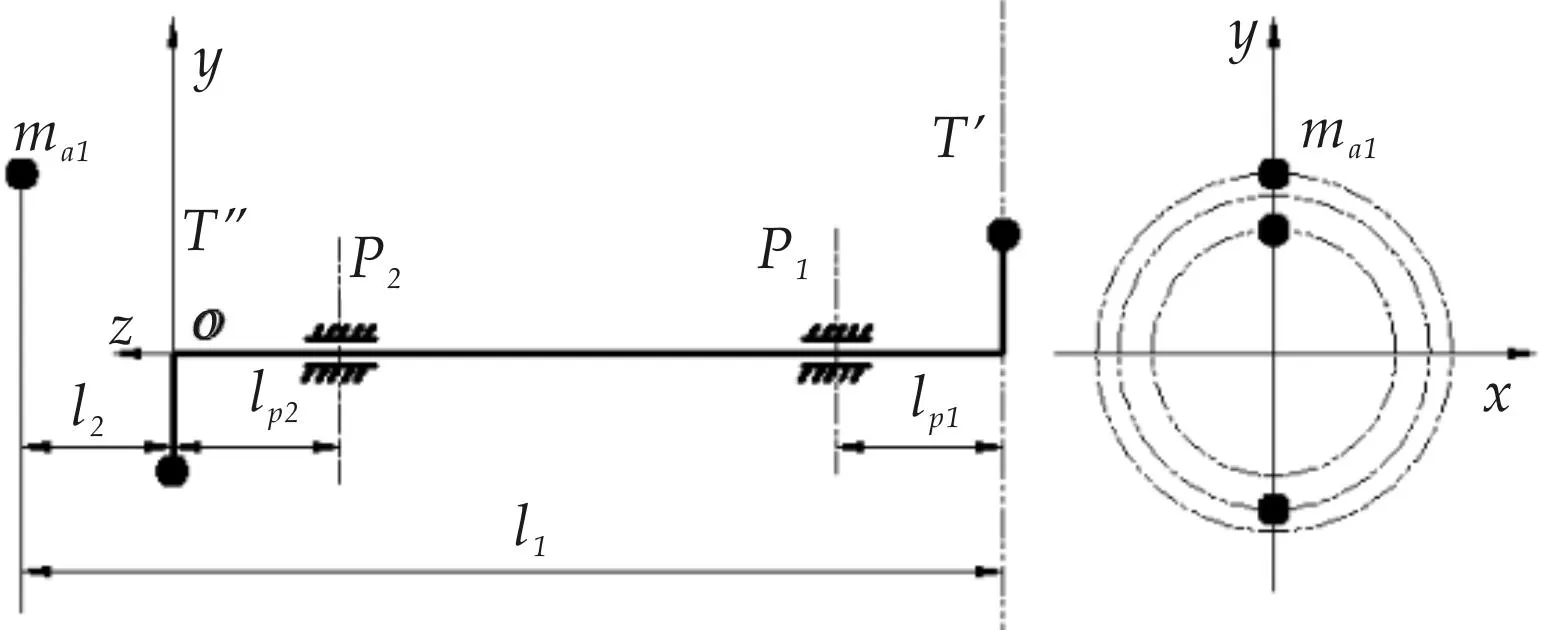
图5　Ⅰ类曲柄单元动平衡示意图

其中θai是广义质量mai的相位角[11,12]，这里取θai=90 °.可得到T′和T″内的配重质量的质径积和相位角，如式(5)、(6)所示.

(5)

(6)

即在面T′、T″面配重的质径积和相位角分别满足式(5)、(6)时，曲柄单元i即是动平衡的.

若不考虑重力因素，任意一个动平衡的曲柄单元在支撑处的支反力为零，也就是说对于由多个已经动平衡的I类曲柄单元和无需动平衡的II类曲柄单元组成的曲柄群机构在分别过支撑点且垂直于回转轴的两个平面P1、P2(如图5所示)内的支反力合力均为零，也就说按照式(5)、(6)对I类曲柄单元进行动平衡后，曲柄群机构是动平衡的.

3算例

对于如图2所示的曲柄群机构，假定o1a1，o2a2和o3a3为I类曲柄，其重量作为配重，o4a4为II类曲柄，质心位于回转含中心.参数如表1所示.

表1　曲柄群机构参数

曲柄回转中心在坐标系xo1y中的坐标(单位m)分别为o1(0，0，0)，o2(0.4，0，0)，o3(0.25，0.3，0)，o4(0.1，0.2，0).

由式(8)、(9)分别求得配重面T′、T″上的配重质量和相位角，如表2所示.

表2　平面T′、T″上的配重质量

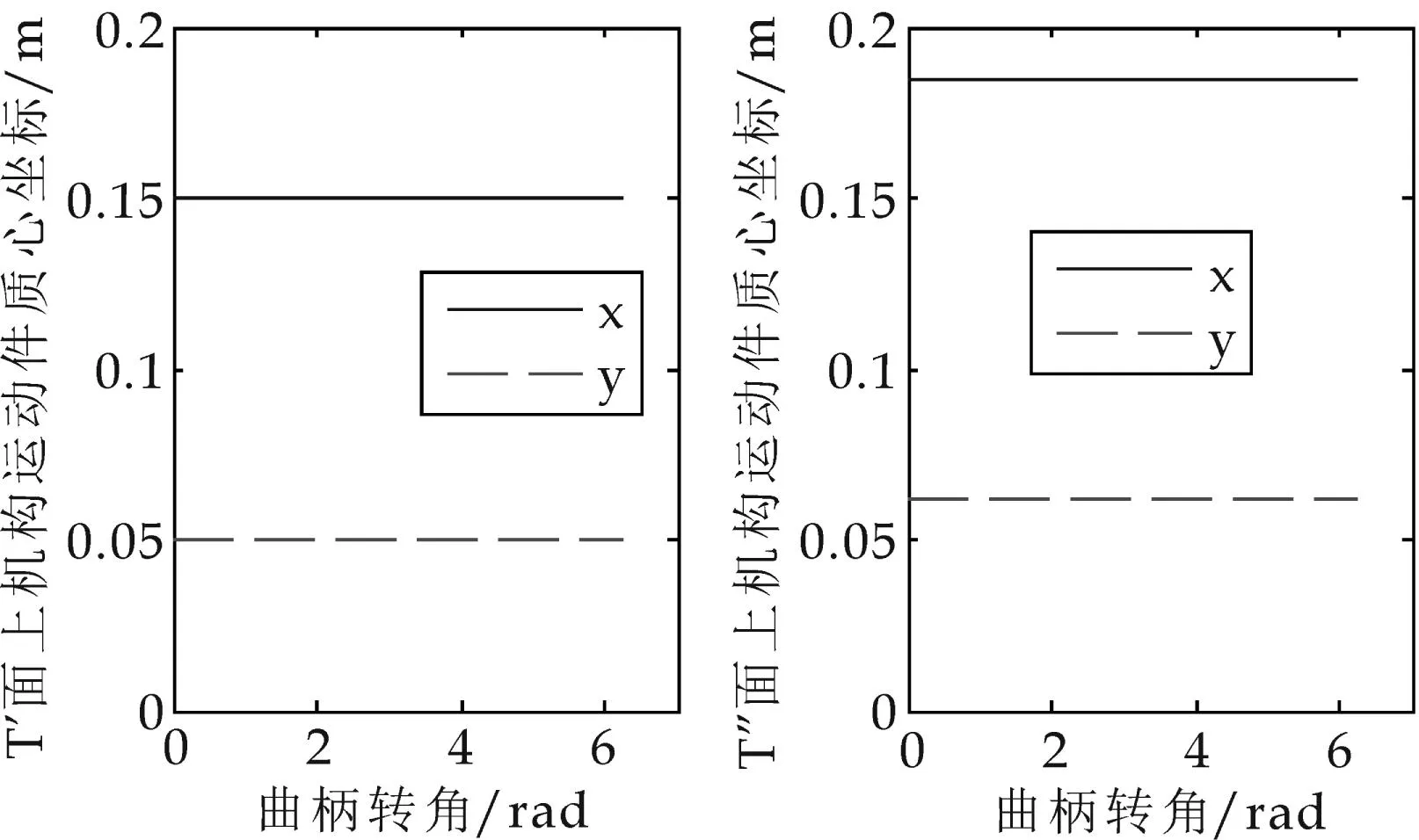
图6　T′、T″上运动件的总质心坐标

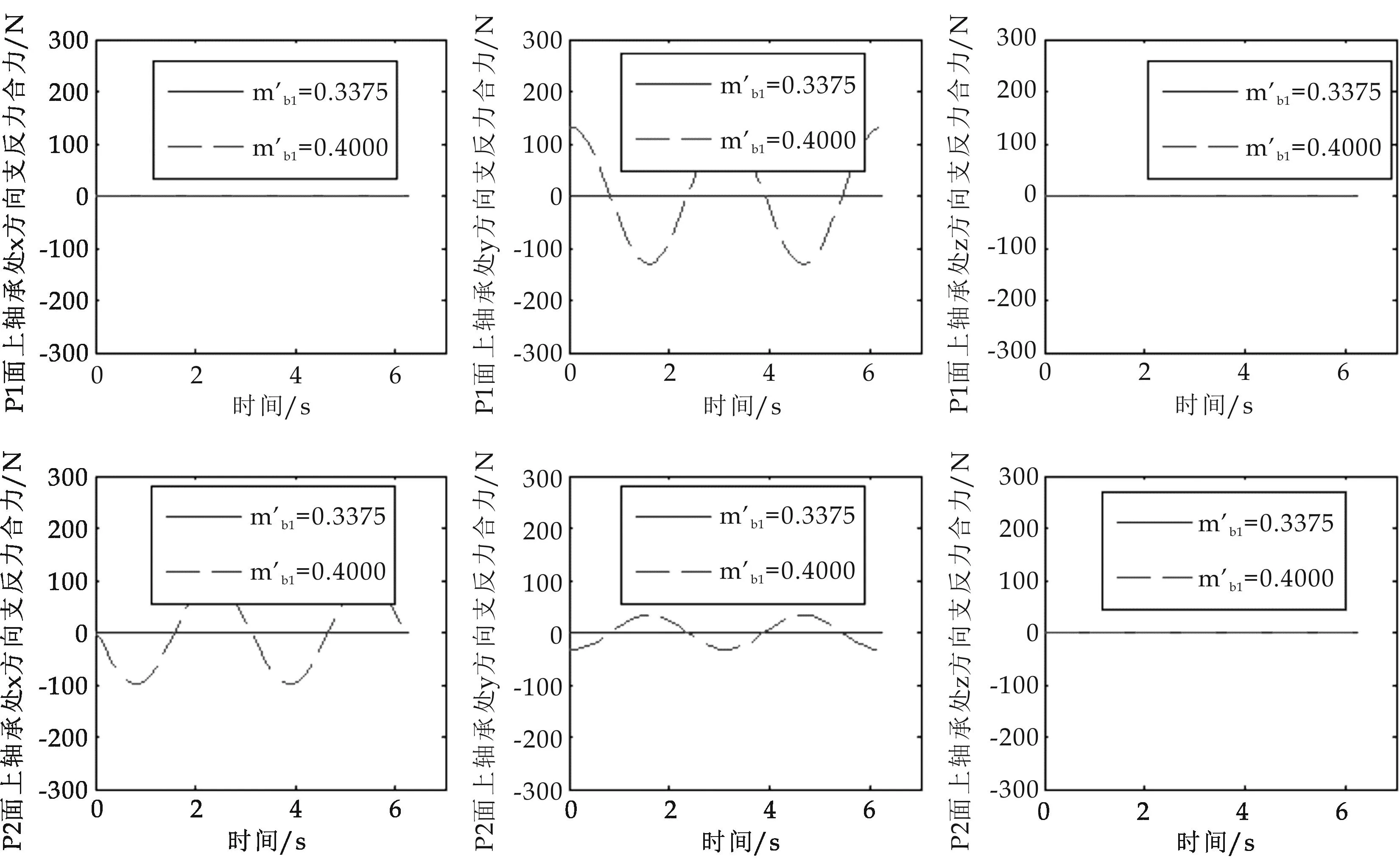
图7　配重后曲柄群机构的支反力合力

4结论

(1)提出了曲柄群单元化的概念.为了在实数域中进行广义质量替代，将曲柄群机构中的连杆桁架质量向三个连杆桁架与曲柄的铰接点替代.将包含替代质量的曲柄定义为一个I类曲柄单元，从而把曲柄群机构的动平衡问题简化为I类曲柄单元的动平衡问题.

(2)证明了通过质量替代为手段，当I类曲柄单元实现动平衡时，曲柄群机构也达到了动平衡.同时也表明，对于含有3个及以上曲柄的曲柄群机构而言，只要通过结构设计完成三个I类曲柄单元的动平衡，即可实现曲柄群机构的动平衡，对于曲柄群的结构设计具有重要的指导意义.

参考文献

[1] 陆文欣.曲拐传动多轴箱单连杆多曲柄机构的设计与应用[J].常州工业技术学院学报，1996,9(2):46-51.

[2] 汪玉琪,曹巨江.曲柄群驱动机构的运动特点研究[J].机械传动,2013,37(10):79-81.

[3] 任升,曹巨江,刘言松,等.曲柄群驱动机构单元化平衡[J].轻工机械,2015，33(1):9-12.

[4] Lyndon O.Barton.Mechanism analysis of a trisector[J].Mechanism and Machine Theory,2008,43(2):115-122.

[5] 汪玉琪,曹巨江.曲柄群驱动机构概述[J].机械传动,2013,37(4):134-136.

[6] 柳志远,冯占广.小型单缸卧式发动机一阶往复惯性力整体平衡法的理论研究[J].农业机械学报,1990(3):23-28.

[7] 任升,曹巨江.基于并联机构理论的曲柄群驱动机构的自由度分析[J].机械设计与研究,2014，30(4):14-16.

[8] 任工昌，王宏卫.双向动平衡检测技术在汽车变矩器上的应用[J].陕西科技大学学报(自然科学版),2014,32(5):137-141.

[9] Yansong Liu,Jujiang Cao,Ren Sheng.Inertia force balance of crank-group driving mechanism based on crank unit [J].The Open Mechanical Engineering Journal,2015(9):601-604.

[10] 杨义勇,金德闻.机械系统动力学[M].北京：清华大学出版社，2009.

[11] 于靖宇.机械原理[M].北京：机械工业出版社，2013.

[12] 马履中,谢俊,尹小琴.机械原理与设计[M].北京：机械工业出版社，2015.

[13] 曾梁彬,孙宇,彭斌彬,等.基于振动响应的一般平面机构动平衡方法[J].中国机械工程,2012，23(13):1 524-1 528.

[14] 刘志鹏.动平衡机振动分析及测试系统研究[D].大连：大连理工大学，2015.

[15] 白志刚.转子振动及动平衡检测系统的研究[D].北京：华北电力大学，2001.

[16] 黄树红,徐煜兵,贺国强，等.多功能轴系动平衡及振动分析系统[J].振动与冲击,2000，19(1):79-84.

【责任编辑：陈佳】

Dynamic balancing of crank group mechanism based on generalized mass substitution

LIU Yan-song， CAO Ju-jiang

(College of Mechanical and Electrical Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China)

Abstract:According to the distribution characteristics of center of mass of the crank group mechanism,the mechanism is broken into some crank units named class I crank unit or class II crank unit,by generalized mass substitution in which the mass of the connecting rod truss is substituted on the 3 hinged points, and the dynamic balancing of the crank group mechanism is converted to the dynamic balance of class I crank unit. The calculation example shows that the crank group mechanism is a dynamic balancing mechanism when each class I crank unit is a dynamic balancing rotor.The conclusions may be helpful for reducing the foundation vibration of the mechanism and simplifying the structure in the design of the crank group mechanism.

Key words:crank group mechanism; generalized mass substitution; crank unit; dynamic balancing

中图分类号：TH112

文献标志码：A

文章编号：1000-5811(2016)03-0142-04

作者简介:刘言松(1975-)，男，安徽凤阳人，讲师，在读博士研究生，研究方向：机械系统动力学、自动机械、冗余机构

基金项目：国家自然科学基金项目(51175313)

收稿日期:2016-04-19