一类DGH方程的多辛Preissmann格式

李胜平，王连堂，王俊杰，

一类DGH方程的多辛Preissmann格式

李胜平1，王连堂2，王俊杰1，2

(1．普洱学院数学系，云南普洱665000; 2．西北大学数学系，陕西西安710127)

DGH方程作为一类重要的非线性方程有着许多广泛的应用前景．基于哈密顿系统的多辛理论研究一类DGH方程的数值解法，利用多辛Preissmann方法对此哈密顿系统进行数值离散，构造一种半隐式的多辛格式．数值算例结果表明该多辛离散格式具有较好的长时间数值稳定性．

哈密顿系统;Preissmann方法;多辛算法;DGH方程

1 预备知识

2001年，R．Dullin，G．Gottwald和D．Holm［1］从Euler方程出发，得到了一类带线性和非线性色散项的新型浅水波方程，即DGH方程

其中，u(x，t)表示x方向的流体速度，m=u－α2uxx表示动量，γ/c0是区间长度的平方，(其中c0=2w)表示线性波速．利用m=u－α2uxx，可以将DGH方程写成

DGH方程包含了2类可积孤立波方程．当α→0时，DGH方程变为KdV方程［2－3］

当γ=0时，DGH方程转化为另一类重要的可积方程，即C－H(Camassa－Holm)方程

方程(1)～(3)引起了国内外学者的广泛关注［4－15］．文献［4］在重力作用下，研究浅水层自由表面水波运动规律时，用哈密顿的方法得到C－H方程．迄今为止，已经发现C－H方程的许多性质，例如，对任意的ω，C－H方程具有一个Lax对和双哈密顿结构，以及无穷个守恒量．对ω=0，C－H方程有尖峰孤立波解和多重尖峰孤波解．文献［6］研究了C－H方程守恒量和初值问题，文献［7］研究了C－H方程的对称性和可积性，文献［8］研究了C－H方程的可积扰动问题．文献［5］研究了一类具有完全非线性对流项和色散项的广义C－H方程，得到该方程具有紧孤立子－compacton解和孤立波解．文献［9］研究了耗散C－H方程，得到该方程存在全局解和全局吸引子，文献［10］继续研究该方程，得到该方程具有行波孤子解及其双孤子解，并首次引入了凹凸孤立子的概念．文献［11］研究了一类广义C－H方程及广义弱耗散C－H方程，并得到了该方程具有一类新的尖峰孤立子解．文献［12］研究了DGH方程解的极限行为、散射理论、整体适定性理论、Gauchy问题的局部适定性理论、孤立波的轨道稳定性、新型尖峰孤立波解，同时也给出了DGH方程的散射数据．文献［13］研究了DGH方程的尖峰孤立波解，文献［14］研究了DGH方程的局部解和整体解问题，同时讨论了方程解的Blow－up，文献［15］研究DGH方程的散射逼近和反散射问题．

然而，由于问题(1)～(3)的非线性，在实际应用中要求得方程(1)～(3)的初值问题的精确解几乎不可能，大部分情况下只能用数值方法来模拟方程(1)～(3)．鉴于此，国内外许多学者试图用数值方法来模拟方程(1)～(3)．而使用传统的数值方法，例如有限差分法、有限元方法、谱方法，这些算法都不是保结构算法，长时间数值模拟时都会严重失真．1984年，我国计算数学大师冯康首次系统提出了哈密顿系统的辛算法，大量实例证实辛算法比传统的数值方法具有明显的优势．然而辛算法在应用求解无穷维哈密顿系统时具有局限性，具体表现在整体守恒的不足．为了克服此缺限性，J．Marsden和T．Bridge从不同的角度对辛算法进行了推广．T．Liu等［16］得到了哈密顿多辛结构和多辛算法．本文只考虑Bridge意义下的多辛算法．经过十几年的发展，国内外学者已经建立了KdV方程、薛定谔方程、KP方程、C－H方程的多辛算法，这些多辛算法都证实多辛算法在长时间数值模拟方面的优势．迄今为止，还没有学者利用多辛算法对DGH方程(2)进行数值模拟．本文利用多辛算法对DGH方程(2)进行数值模拟．方程(2)经过变形以后可以表示为哈密顿系统．本文通过引入正则动量，验证DGH方程(2)具有多辛结构，并证实此格式具有多辛守恒律、局部能量守恒律和动量守恒律．给出了DGH方程(2)的离散多辛Preissmann格式，并证实此格式在离散格式下仍保持多辛守恒律．还给出了DGH方程(2)的离散多辛Preissmann格式的误差分析，此格式具有误差o(△t2+△x2)．最后给出了2个数值模拟，并验证了本文的算法不仅简单，而且有长时间的稳定性．

2 多辛哈密顿偏微分方程的多辛算法

大量偏微分方程都可以写成下列多辛哈密顿偏微分方程［17－38］的形式

其中，M，K∈Rn×n(n≥3)是反对称矩阵．S:Rn→R是光滑函数，称为哈密顿函数，zS(z)为函数S(z)的梯度．系统(5)满足3个局部守恒律，即多辛守恒律、局部能量守恒律和局部动量守恒律．

定理2．1［17］根据Bridges多辛理论，偏微分方程(5)满足多辛守恒律

其中，w，k分别表示t和x方向上的辛结构，具体表达式为

定理2．2［17］根据Bridges多辛理论，偏微分方程(5)满足局部能量守恒律

局部动量守恒律

其中

E为能量密度，F为能量流，I为动量密度，G为动量流．

如果z(x，t)关于x是周期函数或者满足齐次边界条件，(5)式满足整体能量和整体动量守恒律

对于系统(2)，引入正则动量

系统(2)可以表示为下面等价形式

定义状态变量

可以把方程(10)写成多辛哈密顿偏微分方程的形式(5)，其中

哈密顿函数为

方程(10)满足多辛守恒律(6)，其中

方程(10)具有能量守恒律(7)，其中

方程(10)具有动量守恒律(8)，其中

3DGH方程的多辛Preissmann格式及离散守恒律

多辛是哈密顿偏微分方程的一个几何性质，在构造数值方法模拟多辛偏微分方程时，自然希望能反映这个性质．基于这个想法，T．Bridges和S．Reich提出了能保持多辛守恒律的离散数值方法为多辛算法．

定义3．1 若哈密顿系统(5)的离散格式

满足如下离散多辛守恒律

其中

为了研究问题方便，首先引入下面符号，向前差分算子

平均算子

上面的算子满足

及推广的Leibniz法则

利用上面的算子，对x方向进行离散，得到哈密顿系统(5)的半离散格式

用隐式中点辛格式对半离散格式(15)时间方向进行离散，得到哈密顿系统(5)的全离散格式

首先分析半离散格式(15)和全离散格式(16)的离散多辛守恒律．半离散格式(15)是多辛的并且满足离散的多辛守恒律

其中

全离散格式(16)是多辛的并且满足离散的多辛守恒律

其中

下面分析半离散格式(15)和全离散格式(16)的离散局部能量守恒律和动量守恒律．半离散格式(15)满足局部能量守恒律

局部动量守恒律

其中

A．Islas等［22］证明了如果非线性哈密顿系统(5)的哈密顿函数S(z)不是二次函数，则多辛算法(16)不能精确满足局部能量守恒律和动量守恒律，为此引入如下定义．

定义3．2 记

称RE和RM分别是局部能量动量守恒律在Axznj和

处的误差，记称εn和ηn分别是整体能量动量守恒律在和

处的误差，其中

下面应用多辛算法(16)对系统(2)进行数值模拟，并且分析系统(2)的离散多辛守恒律、局部能量和动量守恒律误差．对系统(2)的等价方程(10)应用多辛算法(16)可得

方程(25)满足相应的多辛算法(16)的多辛守恒律(18)，其中

因为系统(10)的哈密顿函数是非线性哈密顿函数，利用定义3．2，方程(25)具有局部能量守恒律误差(21)，其中

具有局部动量守恒律误差(22)，其中

4 误差分析

假设z是充分光滑函数，将函数 z在离散点(ti，xj)处分别关于t和x进行泰勒展开的

其中

方程组(26)经过变形得到

代上面的方程到哈密顿系统(5)得

利用M和K，则方程(10)离散格式可以写成

由(28)式的第一个方程得

对(29)式求导可得

把(30)和(31)式代入(28)式的第二个方程

由(28)式的第三、四、五个方程得到

对上面的方程求导得到

代方程(33)～(35)到方程(32)得到

可以看出本文的算法具有精度o(△t2+△x2)．

5 数值例子

为了说明多辛Preissmann算法的诸多优点，下面利用多辛Preissmann算法离散DGH方程(2)对应的多辛哈密顿方程(10)消去辅助变量 、w、Φ和ψ，得到DGH方程(2)的多辛Preissmann三层格式

在利用上面三层格式进行数值模拟时，可用下面二层格式计算上面三层格式第二层上的初值

下面给出2个数值模拟．

5．1孤立波解 取参数α=1，ω=1，γ=1，考虑下面DGH方程(2)的孤立波的初值问题

由文献［39］，可以得到问题(37)有孤立波解

对计算区域进行均匀剖分△x=0．01，取时间步长△t=0．01，计算到T=50，计算结果见表1、图1和图2．表1给出了有限差分法、多辛Preissmann方法和精确解计算问题(37)的比较．图1给出了DGH方程的初值问题(37)随时间的演化图．图2给出了DGH方程的初值问题(37)的局部能量和动量守恒律误差．

5．2尖峰孤立波解 取参数α=1，ω=1，γ=1，考虑下面DGH方程(2)的尖峰孤立波的初值问题解计算问题(38)的比较．图3给出了DGH方程的初值

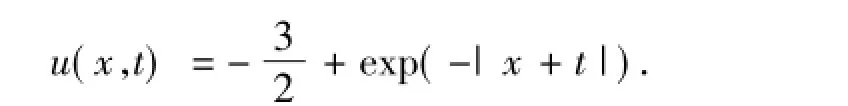
对计算区域进行均匀剖分△x=0．01，取时间步长△t=0．01，计算到T=50，计算结果见表2、图3和图4．表2给出了有限差分法、多辛Preissmann方法和精确

由文献［39］可以得到问题(38)有尖峰孤立波解问题(38)随时间的演化图．图4给出了DGH方程的初值问题(38)的局部能量和动量守恒律误差．

表1 问题(37)有限差分法、多辛Preissmann方法和精确解的比较Table 1 The comparison of finite difference method，multi-sympletic preissmann method and exact solution for question(37)

表2 问题(38)有限差分法、多辛Preissmann方法和精确解的比较Table 2 The comparison of finite difference method，multi-sympletic preissmann method and exact solution for question(38)

本文利用多辛Preissmann方法对一类DGH方程的初值问题进行了数值模拟，图1和图3说明本文的算法能够很好的保持孤子解的基本几何性质，并具有良好的长时间数值行为．从图2和图4说明本文的算法的局部能量守恒律和动量守恒律误差可以控制在10－6．

致谢 普洱学院创新团队基金(CXTD003)对本文给予资助，谨致谢意．

参考文献

［1］DULLIN R，GOTTWALD G，HOLM D．An integrable shallow water equation with linear and nolinear dispersion［J］．Phys Rev Lett，2001，9:4501－4504．

［2］廖欧，舒级，曾群香．一类混合KdV方程的精确孤立波［J］．四川师范大学学报(自然科学版)，2015，38(4):493－496．

［3］赵海云．非线性耦合Schr dinger－KdV方程的新精确解［J］．四川师范大学学报(自然科学版)，2013，36(2):236－239．

［4］CAMASSA R，HOLM D．An integrable shallow water equation with peaked solitions［J］．Phys Rev Lett，1993，11:1661－1664．

［5］LI X，JIU L．New compacton solutions and solltary solutins of fully noniinear generalized Camassa－Holm quations［J］．Chaos，Soliton and Fractals，2004，20:289－299．

［6］FISHER M，SEHIFF J．The Camass－Holm equation:conserved quantities and the initial value problem［J］．Phys Lett，1999，A2593:371－376．

［7］CLARKSON D A，MANSFIEL E L，PRIESLTLE Y T J．Synunetries of a class of noulinear third－order partial differeniial equations［J］．Math Comput Modell，l997，25:195－212．

［8］KRAENKEL R，SENTHILVELSN M，ZENEHUK A．On the integrable periurbations of the Camassa－Holm quation［J］．J Math Phys，2000，41(5):3160－3169．

［9］DAN P，LI X．The attractor in dissipative Camassa－Holm equation［J］．Acta Math Appl Sinica，2004，27:536－545．

［10］LI X，GANG X，ZENG T．The coneave or convex peaked and smooth solutions of Camassa－Holm equatlon［J］．Appl Math Mech，2002，23(5):557－567．

［11］LI X，XIU Y．New peaked solitary wave solutions of the generalized Camassa－Holm equation［J］．Chaos，Solutions and Fractals，2004(3):621－637．

［12］LI X，GUI L，YUE L．On the well－Posedness problem and the scattering problem for DGH equatlon［J］．Commun Math Phys，2005，2573:667－701．

［13］GUO B，LIU Z．Peaked wave solutions of CH－gamma equation［J］．Sci China，2003，A334:325－337．

［14］ZHAO Y．Well－Posedness，blow up and global existence for an Integrable shallow waterequation［J］．Discrete Cont Dyn Syst，2004，11:393－411．

［15］LIN J．On solution of the Dullin－Gottwald－Holm equation［J］．Intre J Nonl Seience，2006，1:43－48．

［16］LIU T，QIN M．Multi－symplectic geometry and multi－symplectic preissmann scheme for the KP equation［J］．J Math Phys，2002，43(8):4060－4077．

［17］TIAN Y，QIN M，ZHANG Y，et al．The multi－symplectic numerical method for Gross－Pitaevskii equation［J］．Comput Phys Commun，2008，178(6):449－458．

［18］WANG Y，WANG B，QIN M．Concatenating construction of multi－symplectic scheme for 2+1 dimensional sine－Gordon equation［J］．Sci China，2004，A47(1):18－30．

［19］ESCHER J，LECHTENFELD O，YIN Z．Well－posedness and blow－up phenom－ena for the 2－component Camassa－Holm equation［J］．Discrete Cont Dyn Syst，2007，19:493－513．

［20］KONG L，LIU R，ZHENG X．A survey on symplectic and multi－symplectic algorithms［J］．Appl Math Comput，2007，186:670－84．

［21］LEIMKUHLER B，REICH S．Simulating Hamiltonian Dynamics［M］．Cambridge:Cambridge University Press，2004．

［22］ISLAS A，SCHOBER C．Backward error analysis for multisymplectic discretization of Hamiltonian PDEs［J］．Math Comput Simulation，2005，69:290－303．

［23］MOORE B，REICH S．Backward error analysis for multi－symplectic integration methods［J］．Numerische Mathematik，2003，95:625－652．

［24］张宇，邓子辰，胡伟鹏．Sine－Gordon方程的多辛Leap－frog格式［J］．应用数学与力学2013，34(5):437－444．

［25］王雨顺，洪佳林．哈密尔顿偏微分方程多辛算法［J］．应用数学与计算数学学报，2013，27(2):163－230．

［26］WANG Y，HONG J．Multi－symplectic algorithms for Hamiltonian partial differential equations［J］．Commun Appl Math Comput，2013，27:163－230．

［27］CAI J，WANG Y，LIANG H．Local energy－preserving and momentum－preserving algorithms for coupled nonlinear Schr dinger system［J］．J Comput Phys，2013，23:930－50．

［28］CELLEDONI E，GRIMM V，McLACHLAN R，et al．Preserving energy resp dissipation in numerical PDEs using the“AverageVector Field”method［J］．J Comput Phys，2012，231(20):6770－6789．

［29］CHEN Y，SONG S，ZHU H．Multi－symplectic methods for the Ito－type coupled KdV equation［J］．Appl Math Comput，2012，218:5552－5561．

［30］LYU Z，WANG Y，SONG Y．A new multi－symplectic integration method for the nonlinear Schr dinger equation［J］．Chin Phys Lett，2013，30(3):1－4．

［31］GONG Y，CAI J，WANG Y．Multi－symplectic Fourier pseudospectral method for the Kawahara equation［J］．Comput Phys Commun，2013，16(1):35－55．

［32］QIAN X，SONG S，GAO E，et al．Explicit multi－symplectic method for the Zakharov Kuznetsov equation［J］．Chin Phys，2012，B21(7):1－6．

［33］WANG J，WANG L．Multi－symplectic Preissmann scheme for a high order wave equation of KdV type［J］．Appl Math Comput，2013，87:4400－4409．

［34］陈璐，王雨顺．保结构算法的相位误差分析及其修正［J］．计算数学，2014，36(3):271－290．

［35］蔡文君．几类无穷维哈密顿系统的保结构算法研究［D］．南京:南京师范大学，2014．

［36］王俊杰，王连堂．一类广义Cammassa－Holm方程的多辛Preissmann格式［J］．系统科学与数学，2013，33(11):1321－1331．

［37］王俊杰．弹性波方程的多辛Preissmann格式计算［J］．地球物理学进展，2014，29(4):1758－1765．

［38］王俊杰，王连堂．一类二次KdV类型水波方程的多辛Fourier拟谱方法［J］．数值计算与计算机应用，2014，35(4):241－254．

［39］殷久利，田立新．一类非线性色散方程中的新型奇异孤立波［J］．物理学报，2009，58(6):3632－3636．

Multi-symplectic Preissmann Methods for DGH Equation

LI Shengping1，WANG Liantang2，WANG Junjie1，2

(1．Department of Mathematics，Puer College，Puer 665000，Yunnan; 2．Department of Mathematics，Northwest University，Xi’an 710127，Shannxi)

DGH equation which is a typical nonlinear wave equation，has broad application prospect．In this paper，the equation is studied based on the multi-symplectic theory in Hamilton space．The symplectic Preissmann method is used to discretize the formulations，and a semi-implicit scheme with certain discrete conservation laws is constructed to solve the DGH equation．The numerical experiments are given，and the results verify the efficiency of the multi-symplectic scheme．

Hamilton system;Preissmann method;multi-symplectic theory;DGH equation

O29

A

1001－8395(2016)05－0696－09

10．3969/j．issn．1001－8395．2016．05．015

(编辑 李德华)

2014－12－14

云南省教育厅自然科学重点基金(2015Y490)

李胜平(1957—)，男，教授，主要从事微分方程的研究，E－mail:pexylsp@163．com

2010 MSC:35F21;37K05