SAT数学考试改革研究——兼议对我国高考改革的启示

任子朝 陈 昂

SAT数学考试改革研究
——兼议对我国高考改革的启示

任子朝 陈 昂

为适应现代社会对人才的需要，美国教育考试服务处对美国大学入学考试SAT进行了改革。改革后的SAT数学考试更注重与学生课堂学习的联系，更强调对数学概念的理解，进一步加强了对逻辑推理能力和计算能力的考查；对数学运算的准确和熟练程度都提出了更高的要求；在丰富的应用场景中，考查数学在职业、科学和在社会研究中的应用；试卷的长度加长，综合程度提高。这些都为我国的高考改革提供了有益的启示和借鉴。

SAT考试；高考；核心素养

随着全球化、信息化时代与知识社会的来临，现代公民应具备哪些最基本、最重要的知识、能力和情感态度，才能更好地促进个人自我实现与成功地生活？这些问题已经进一步转化为当下世界各国基础教育课程改革重点关注的核心问题。[1]目前，世界各主要国家纷纷启动了学生“核心素养”的研究，并在此基础上开启了新一轮基础教育课程改革和考试改革。美国教育考试服务处（ETS）对SAT进行了长期的改革研究，2016年3月推出新SAT考试。对SAT考试改革进行分析研究，吸取其有益的做法和经验，将对我国的高考改革起到启示与借鉴作用。

SAT全称为Scholastic Assessment Test，即学术能力评估测试，其地位和作用基本与中国的高考相当。SAT考试创设时的理念是，首先独立于美国高中课程，其次满足美国大学考查学生学术能力的要求，第三是测评考生批判性思维及阅读、写作能力。SAT第一次考试于1926年举办。在80多年的发展历程中，它已经历了1994年和2005年两次重大的改革，但本次改革却是其发展历史上最大的一次改革。[2]近年，美国的企业界与教育界共同提出“21世纪能力”（21st Century Skills）的概念，在学科内容的知识之上，加上了在21世纪社会生存所必须的高阶认知能力——“学习与革新：4C”，即“批判性思维”（critical thinking）、“沟通能力”（communica⁃tion）、“协同”（collaboration）与“创造性”（creativi⁃ty）。[3]在这样的背景下，ETS对SAT的考试内容和形式进行了全面改革。新SAT包括三个部分：基于证据的阅读和论述、数学和写作（见表1）。其中，写作是选考，考生可以自由选择。新SAT考试的核心是分析证据，围绕这个核心，它提出了8个方面的改革内容，包括理解相关情景中的名词、掌握和运用证据、在写作中分析信息、数学核心知识、实际生活问题、跨学科问题分析、理解美国建国和国际对话文件以及答错不再倒扣分。本文将对SAT数学部分的改革进行分析，总结其对我国高考改革有益的做法和经验。

表1 整体试卷结构

1 改革的基本指导思想

现代社会需要人们能够解决问题、清晰地表达和交流以及理解复杂的关系。这些关系可能是在自然界、未来的市场或小说中存在。现实研究表明，学生还没有完全做好准备以参与需要这些技能的职业中。[4]美国大学委员会试图让SAT提供一个更好的、可以全面描述学生对大学学习准备情况的评价测验，使考试能更清晰地考查知识、技能和理解能力，同时可以反映学生的学习情况。

2 SAT数学试卷结构及考试内容

SAT数学试卷结构见表2，其中四选一选择题45题，主观题13题。与过去相比，新SAT进一步加强了测评与学生课堂学习内容的紧密联系，更加注重数学知识间的系统联系，所涉及的内容都是今后日常生活、大学学习中涉及的知识，主要包括：[5]

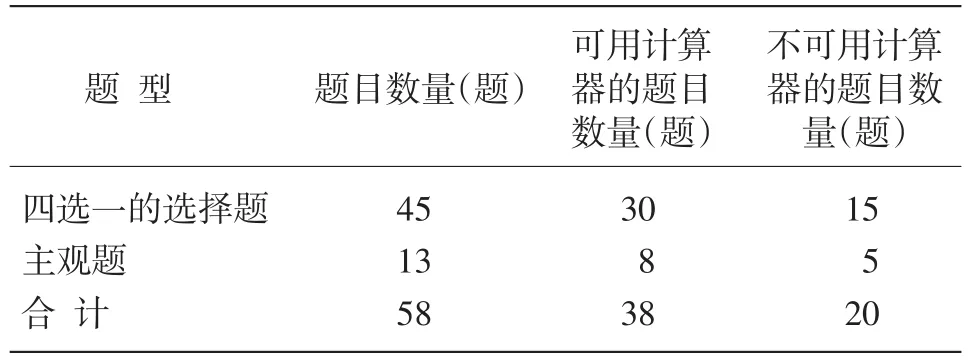
表2 数学试卷结构

核心代数（19题）：线性方程和线性方程组，利用线性方程和一次不等式表示数量关系并解决问题，理解并应用线性方程和一次不等式的图像解决问题。

问题解决和数据分析（17题）：利用比、百分比及单位，分析数据，发现并应用概率。

高等数学基础（16题）：等价的代数表达式，能够列出、解决二次方程和其他非线性方程，能够应用指数函数、二次函数和其他非线性函数。

附加数学专题（6题）：解决面积、体积问题，应用直线、角、三角形、圆的定义和定理解决问题，能够应用直角、单位圆和三角函数。

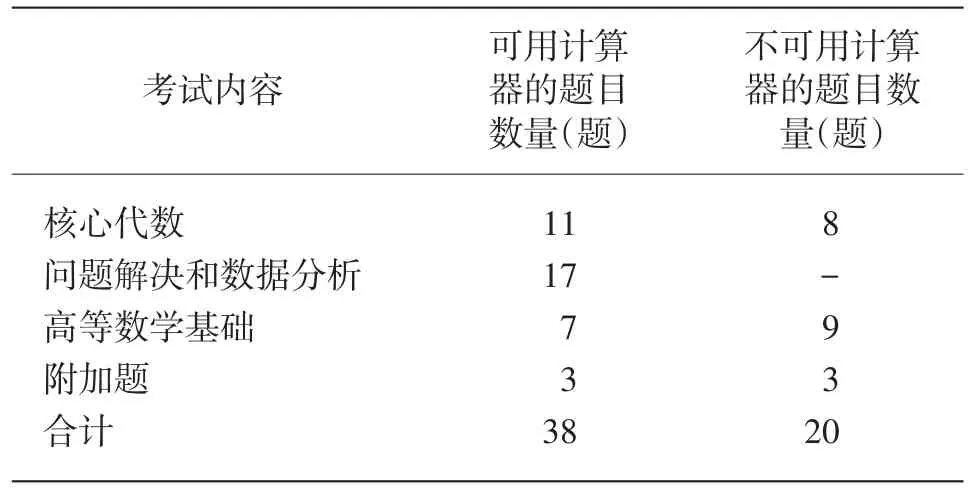
表3 数学试卷内容比例

3 数学考试改革要点

重新设计的SAT数学测试旨在从下列角度描述学生的学习情况：学生是否熟练地掌握、理解并且能够运用对于他们大学生涯和职业训练至关重要的数学概念、技能和实用技巧。ETS认为理解能力、推理和运算能力以及在学习和工作中应用数学的能力是至关重要的。

为了在重新设计后的SAT数学测试中取得好成绩，学生需要展现出强大的数学应用能力，例如问题解决和有策略地运用工具。因此，SAT提供了大量的应用类问题。

在重新设计SAT的过程中，ETS一直在努力采用最新的研究成果来调整测试时限、问题数量和结果报告。所进行的调整都是为了使得测验更加有效，也就是充分利用题目信息，更准确地考查学生的数学能力。新SAT数学考试体现了以下特点。

3.1 更强调基于数学的逻辑推理和运算

本题给出的条件是一个二元一次方程，不可能分别解出两个未知数的值，因此需要通过观察方程左边两个代数式的关系求解。注意到两个代数式中两个未知数系数的关系，第二个式子是第一个式子的6倍，通过这个关系就能解题。

3.2 强调对数学概念的理解

例2.平流层在地球表面以上10 km到50 km的区域，下面哪个不等式中的x表示了在地球表面以上平流层的高度？

（A）|x+10|＜50 （B）|x-10|＜50

（C）|x+30|＜20 （D）|x-30|＜20

本题考查了不等式的概念和性质，是逆向思维的过程。平流层的高度x可以用不等式10＜x＜50，不等式的两边同时减去30，则可变形为|x-30|＜20。当然也可以将4个不等式分别变形后，与不等式10＜x＜50进行对比，但工作量显然较大。

本题是二元一次方程组，不可能找出计算xy的简便算法，而是要求学生分别算出x和y的值，再进行相乘。本题要求学生掌握二元一次方程组的解法，按照规定的步骤解题，对于知识和方法不仅能理解而且还能熟练应用。

3.3 在丰富的应用场景中，考查数学在职业、科学和社会研究中的应用

例4.图1是1991年到2011年佛罗里达海牛数量的散点图，则海牛年平均增长的数量是

（A）0.75 （B）75

（C）150 （D）750

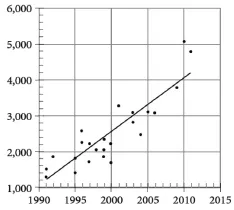
图1

本题基于在美国渔业和野生动物服务中心调查海牛数量时用到的真实方法。题目把线性方程和统计相结合，并且深入考查直线斜率的实际意义。在这道题中，学生不需要进行完整的建模，只需要明确题目要求他们计算的是直线的斜率，并且理解直线斜率的意义。

例5.如果一个装有某种气体的容器有大于气体分子的小孔，则气体将会逸出，这个过程称为扩散.如果一种摩尔浓度为M1气体以r2速度扩散，另一种摩尔浓度为M2气体以r2速度扩散，则存在如下关系，这被称为格雷厄姆定律.根据此定律，则M2=

试题以自然科学中的气体扩散为背景，属于跨学科问题。考生需要理解等式所蕴含的比例关系，从而得出结论。下面的问题属于问题解决和数据分析，都是统计学的原理和方法在实际中的应用。

例6.相机电池的寿命可以用其所拍照片的数量计算.一电子公司的质检员要检测某种相机电池的寿命，他在某日产出的电池中随机挑选了100个进行检测，发现在95%的置信区间，电池可以照相324～360张.下面哪种说法是最合理的？

（A）该公司当天生产的所有电池有95%的电池寿命在324～360张照片之间

（B）该公司曾经生产的电池有95%的电池寿命在324～360张照片之间

（C）似乎可以说该公司当天生产电池真正平均寿命在324～360张照片之间

（D）似乎可以说该公司曾经生产的电池有95%的电池寿命在324～360张照片之间

3.4 设置多个问题的场景，考查更加深入

新SAT设计了如下几种问题：（1）与职业相关的情景，需要估计、计算百分比和相关关系；（2）同一个题干下有多个设问；（3）涉及复杂结果的现实生活情景；（4）非线性的现实问题，需要画图或者计算回报。

例7.国际银行在全球范围内发售旅游信用卡，当旅行者在其他国家用信用卡消费时，银行按当日的汇率将消费额转换成本国货币数量，并加收4%的手续费.美国公民塞拉去印度度假，她用信用卡消费了602卢比，银行共向她收费9.88美元，其中包括4%的手续费.

问题（1）计算当天的汇率，精确到整数.

问题（2）印度的一家银行售卖一种7 500卢比的预付卡，塞拉可以按当天的汇率用美元购买该卡且不收手续费，但卡中没有消费的剩余钱将不再退还.如果塞拉购买这种卡，她要至少要消费多少卢比才比用信用卡便宜？精确到整数.

本题以旅游和刷卡消费为背景设计了汇率计算的问题。由于与社会生活紧密结合，有一定的思维量。

3.5 不可使用计算器的试题考查运算能力以及数学运算的准确和熟练程度

不可使用计算器的试题主要是测试学生运算的熟练程度以及对数学概念的掌握情况。

本题考查考生同解变形的能力和数学计算的熟练度、准确度。

4 思考与借鉴

新SAT数学考试的特点对我国的高考数学改革提供了可供借鉴的范例和经验。

4.1 注重对数学知识的系统考查，与学生课堂学习联系更加紧密

经历近百年的沿革，SAT改革却再次要求更贴近中学教学。[6]新SAT不仅删除了一些脱离中学课程、单纯测试推理能力的试题，而且增加了更多反映中学生实际所学内容的试题。改革后的SAT对推理能力的测试并不是抽象地展开，而是联系中学课程和学科内容测试学生的推理能力。虽重在考查学生的分析推理能力，但SAT试题需要中学基础知识的支撑，更注重平时的系统积累和刻苦训练。因此，如果不学好高中课程，学生很难取得好成绩。

4.2 重视对于数学概念的理解和运算能力的考查

计算器只在数学的一个部分被允许使用，改变了以往所有数学试题都可以使用计算器的规定。尤其这次改革要求学生理解数学的本质，对学生的数学推理方法和运算能力都提出更高的要求。不可使用计算器的部分试题达到了34.5%，其目的在于测查考生对于数学概念的理解能力，而非重点评估考生的计算能力。[7]SAT并不属于智力测验的范畴，而是通过要求学生“运用高中所学”测量学生的推理与批判性思维技能。

4.3 新SAT考试的核心是分析证据

美国大学委员会邀请中学和大学教师设计题目，让学生能用数学分析经济学或科学实验结果的数据。改革后，数学考试的难度进一步加大，对推理能力的要求提高，更加重视应用数学知识和方法分析、推理的能力，更强调实用性和逻辑性。

4.4 注重数学在不同学科中的应用

在全面关注数学与中学各科联系的基础上，加强数学在其他学科的应用是SAT考试改革的重要举措。在新的试卷结构中明确了与自然科学、社会历史科学相关的试题的比例。这是时代发展的要求。特别是随着大数据的发展，社会历史等学科对数学的需求也越来越多，要求也越来越高，这点值得我国的高考改革关注和借鉴。

[1]左璜.基础教育课程改革的国际趋势：走向核心素养为本[J].课程·教材·教法，2016（2）:39-46.

[2]杨光富.美国大学入学考试SAT改革述评[J].全球教育展望，2015（1）:83-91.

[3]钟启泉.基于核心素养的课程发展：挑战与课题[J].全球教育展望，2016（1）:1-24.

[4][5]College Board.The Official SAT Study Guide[M].New York:Mac⁃millan，2014:225.

[6]张睦楚，汪明.美国新一轮SAT考试改革的争议与评析[J].上海教育科研，2015（10）:24-27.

[7]刘谦，姚曼.美国大学入学考试SAT的变迁[J].外国教育研究，2015（9）.

Research on the Reform of SAT Math Test: Implications for the College Entrance Examination Reform in China

REN Zizhao&CHEN Ang

In order to meet the needs of modern society,Educational Testing Service（ETS）carried out a reform of the United States university entrance examination SAT.The reformed SAT math test pays more attention to the knowledge that students learned in the classroom,and focuses on understanding of mathematical concepts,logical reasoning and computing ability.The reformed SAT math test makes higher requirements on mathematical skills.It tests the applications of math in different areas,such as career,science and society.Compared to the College Entrance Examination in China,the SAT math test is more comprehensive and includes more test items.SAT’s reform provides a useful lesson for China’s College Entrance Examination reform.

SAT;College Entrance Examination;Core Competencies

G405

A

1005-8427（2016）06-0020-5

（责任编辑：陈睿）

本文系全国教育科学规划教育部重点课题“高考能力考查与内容改革创新研究”（课题编号：GFA111006）的研究成果之一。

任子朝，男，教育部考试中心，研究员（北京 100084）

陈 昂，男，教育部考试中心，助理研究员（北京 100084）