非线性RLC电路的新解法及数值仿真*

黄 偲,余顺争

(1. 中国能源建设集团广东省电力设计研究院网络信息部，广东 广州 510663;2.中山大学电子和通信工程系，广东 广州 510275)

非线性RLC电路的新解法及数值仿真*

黄 偲1,余顺争2

(1. 中国能源建设集团广东省电力设计研究院网络信息部，广东 广州 510663;2.中山大学电子和通信工程系，广东 广州 510275)

给出一类非线性RLC电路的新解法及数值仿真：电路的状态变量表示为相位角简谐函数；电路状态方程的求解归结为相位角对时间的一阶导数的确定；时间自变量与中间变量相位角的关系由响应频率倒数的积分表示；从而算出电路的相轨线、时程曲线、相程曲线、时幅曲线、相幅曲线、幅频曲线、相频曲线和响应周期，数值仿真显示，结果与数值积分法吻合良好。

非线性RLC电路；状态方程；新解法；数值仿真

由RC、RL、RLC构成的串联电路，在RLC串联电路的不同过程中具有不同的特性，包括暂态特性、稳态特性、谐振特性，这些状态特性是RLC电路设计需要解决的关键问题。

非线性RLC电路状态变量之间的变化关系可由以下的非线性微分方程

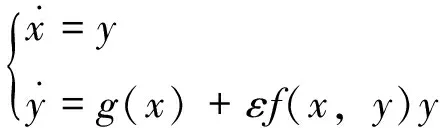
(1)

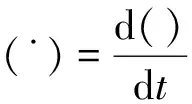
1 新解法概述

将式(1)改写为

或

ydy=g(x)dx+εf(x,y)ydx

上式两边对x由零开始积分，得

(2)

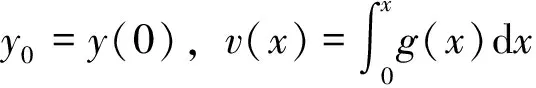
直接假设非线性RLC电路(1)的状态变量为相位角φ简谐函数

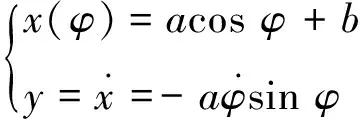
(3)

这里，a和b待定常数，分别表示振幅和偏心距，

(4)

是中间变量相位角φ与时间自变量t微分关系，也表示电路状态变量的响应频率。式(4)变形为

(5)

式(5)两边对φ积分，得

(6)

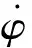
(7)

(8)

v(-a+b)-v(a+b)+

(9)

式(6)中取φ=2π且t0=0则电路的稳态周期为：

(10)

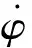
(11)

迭代格式为：

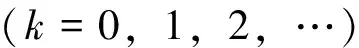
(12)

电路的状态变量的k阶近似解为：

(13)

其中ak和bk由以下二式解出：

(14)

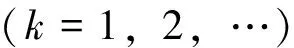
(15)

k阶近似的时-相变换式及响应周期分别为：

(16)

(17)

2 应 用

考虑如图1所示的电容库伏特性为荷控型RLC串联电路[1]，其非线性电容C的库伏特性为

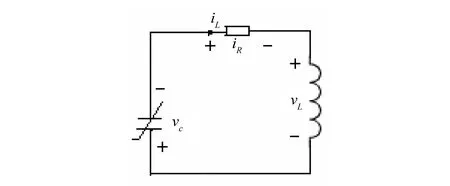
图1 RLC串联电路 Fig.1 RLC series circuit

v=f(q)=-q+q3。电阻R和电感L均为线性。以电荷q和电感电流iL为状态变量，电路的状态方程可表为

(18)

试讨论该电路的周期振荡解。

令x=q,y=iL,L=1，式(18)化为

(19)

自治电路的状态方程(19)有三个平衡点(0,0),(-1,0), (1,0)，前者是鞍点，绕该点电路无稳定周期振荡；后二者是渐近稳定焦点。下面讨论环绕焦点的周期振荡解。

首先考虑电路绕焦点(1,0)的振荡。作x坐标的平移变换

式(19)变为

(20)

比较式(1)得

用上述的迭代法近似求解之。无阻尼(δ=0)时，由式(11)及(19)得电路(20)的初始频率

(21)

其中,

(22)

将式(21)展开为泰勒展开式，并取前二次项(为书写方便，记a=a0,b=b0)，得

(23)

将式(23)代入式(14)、(15)，并注意到式(20)，分别得

(24)

(25)

将式(23)代入式(12)可得

(26)

其中,

联立式(24)和(25),并注意到式(22)得

a2=-2b-b2

(27)

Aa4+Ba2+C=0

(28)

其中，

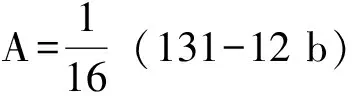
C=64+384b+768b2+576b3+144b4

由式(28)得

(29)

联立式(27)及(29)，得

C=B(2b+b2)-A(2b+b2)2

化简上式可得

1 971b2+1 584b+256=0

此方程有三个近似实根

b=-37.883 833; -2.347 637; -0.208 053

由a>0及式(28)知，只有最后者符合题意，此时，

(30)

从而得到电路(20)的一次迭代的近似解

(31)

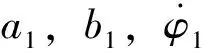
电路过点鞍点(-1,0)有同宿轨线，其表达式仍具有式(31)的形式，但幅值与偏心距由以下二式确定

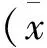
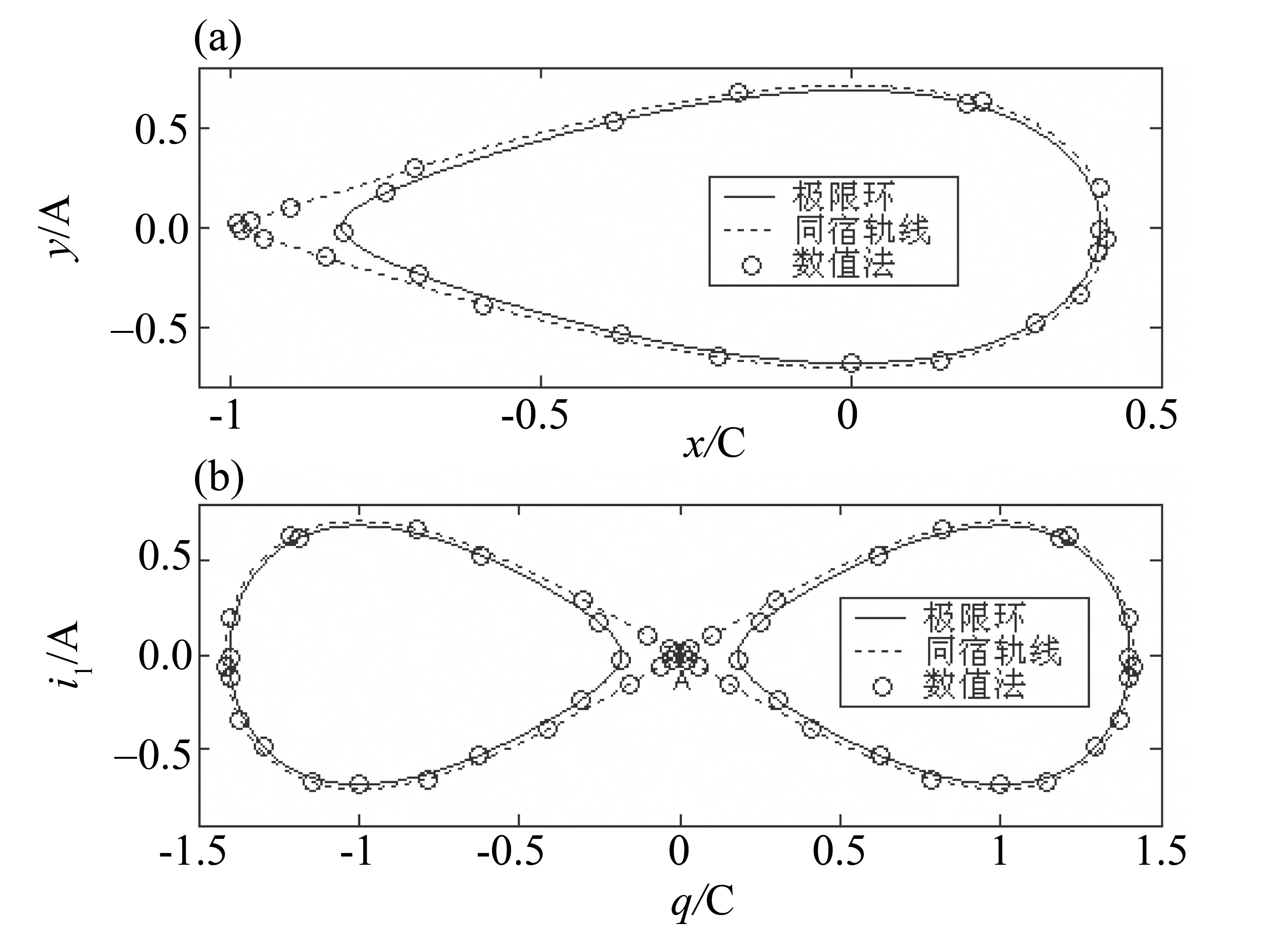
图2 电路(18)的极限环与同宿轨线Fig.2 Limit cycle and a homoclinic orbit of the circuit (18)

2r3r5cos3φsinφ+2r3r7cos3φsin3φ+

2r4r5sin2φcosφ+2r4r6sin4φ+

2r5r7sin4φcos2φ+2r6r7sin6φcosφ+

2(r2r7+r3r6)cos2φsin3φ+

(6r2r4-4r1r5)sinφcosφ+

(6r2r6-4r1r7)sin3φcosφ}

由式(16)得一次迭代的时间t与相位角φ的关系式

(32)

其中，

c2=-4r1r2+6r2r3,c3=4r1(r4+r6)

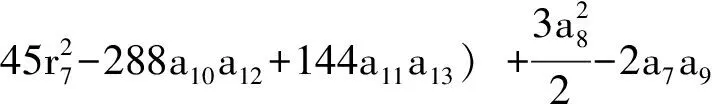
c5=3r2r4-2r1r5,

c7=-2r2r3+4r4r5

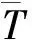
本法计算的幅频曲线和相频曲线如图4。

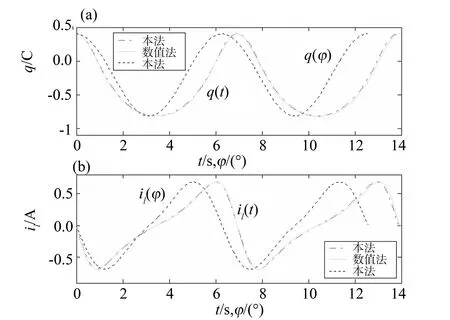
图3 电路(18)的电量及电流与时间和相位的关系曲线Fig.3 Curves of the relationship between power and current with time and phase of the circuit (18)

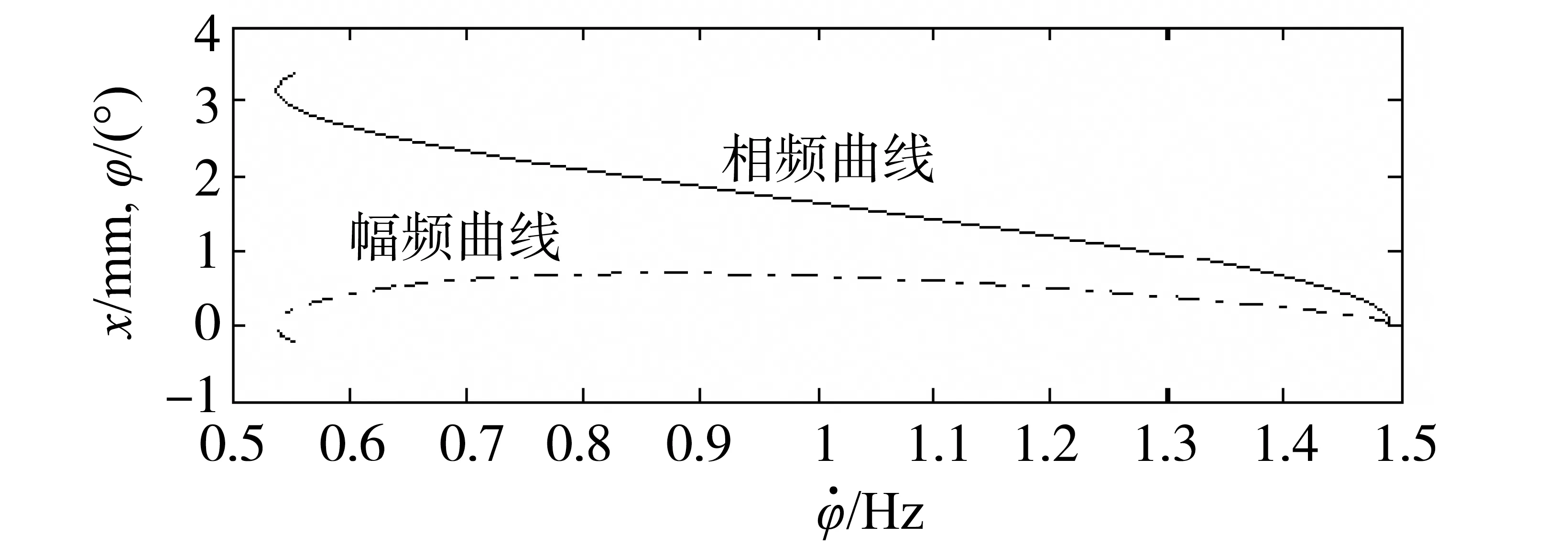
图4 电路(18)的幅频曲线和相频曲线Fig.4 Amplitude frequency curve and phase frequency curve of the circuit (18)

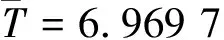
数值搜索及本文的方法显示，RLC串联电路(18)仅当电阻R与电感L数值上的比值δ较小，比如δ=0.000 1附近才能实现稳态振荡，这在工程上具有实用意义。

3 结 语

本文提出的新解法仅涉及初等微积分，理论依据可靠；计算结果仅一次近似便与数值解法(一般认为是精确解)的误差已小于3.4%，如此高精度解析方法，对非线性RLC电路设计将具有很好的实用价值。

[1] 邱关源. 现代电路理论[M]. 北京：高等教育出版社，2006.

[2] 郑近德，程军圣，曾鸣 . 基于改进的局部特征尺度分解和归一化正交的时频分析方法[J].电子学报，2015，43(7)：1418-1424.

[3]GIAOURISD,BANERJEES,IMRAYEDO,etal.Complexinteractionbetweentoriandonsetofthree-frequencyquasi-periodicityinacurrentmodecontrolledBoostconverter[J].IEEETransactiononCircuitsandSystemsI:RegularPapers, 2012,59(1):207-214.

[4]YESOOHAV,KAVIPRIYAR,JOSHNTS,etal.AnalysisofchaosandbifurcationinDC-DCconverterusingmatlab[C]∥InternationalConferenceonCircuits,PowerandComputingTechnologies.Nagercoil:IEEE, 2013:481 -487.

[5] 罗晓华，罗诗裕.三束储存与电子同步运动的动力学稳定性[J]. 中国科学(物理学，力学和天文学)，2014，44(2)：169-175.

[6]RATHEEA，PARTHASARATHYH.Perturbation-basedstochasticmodelingofnonlinearcircuits[J].CircuitsSystemsSignalProcess, 2012, 32(1): 123-141

[7]FINGERL，UHLMANNH.Effectivecomputationofthepoincaremapfortheanalysisofnonlineardynamiccircuits/systemsusingrunge-kuttatriples[J].JournalofCircuitsSystem&Computers, 2011, 4(1)：93-98.

[8]JIAOD，ZHUO.Methodforaccurateandefficientsignalinganalysisofnonlinearcircuits[C]∥IEEESymposiumonElectromagneticCompatibilityandSignalIntegrity, 2015.

[9]KOLKSZ,BIOLEKD，BIOLKOVAV.Frequency-domainsteady-stateanalysisofcircuitswithmem-elements[J].AnalogIntegratedCircuits&SignalProcessing,2013, 74(1):79-89

[10]GARCIAN.Periodicsteady-statesolutionsofnonlinearcircuitsbasedonadifferentiationmatrix[C]∥CircuitsandSystems(ISCAS),Proceedingsof2010IEEEInternationalSymposium, 2010.

[11]ANGELONEG，VASCAF，IANNELLIL.Dynamicandsteady-stateanalysisofswitchingpowerconvertersmadeeasy:Complementarityformalism[C]∥DynamicsandControlofSwitchedElectronicSystems, 2012:217-243.

[12]MOHAMMADJS，YASSRMB.GeneralSPICEmodelsformemristorandapplicationtocircuitsimulationofmemristor-basedsynapsesandmemorycells[J].JournalofCircuitsSystem&Computers, 2010, 19(2):407-424.

[13] 姚齐国. 几种非线性电路的数值分析与优化设计[D].武汉： 华中科技大学,2007.

[14] 孙璐. 基于散射函数的一种微波非线性电路建模新方法,[D].西安：西安电子科技大学,2010.

[15] 张晓芳，陈章耀，毕勤胜. 非线性电路通向混沌的演过程[J]. 物理学报，2010，59(5)：3057-3065.

The new solution and numerical emulation for a nonlinear RLC circuits

HUANGCai1,YUSunzheng2

(1．Network & Telecommunication Division, China Energy Construction Group Guangdong Electric Power Design & Research Institute, Guangzhou 510663, China;2．Department of Electronics and Communication Engineering, Sun Yat-sen University,Guangzhou 510275, China)

A new solution and its numerical emulation for the nonlinear RLC circuit are given. The state variable of the circuit is expressed as the simple harmonic function of the phase angle. The determination for the first derivative of the phase angle about the time are used to solve the state equations. The relation of the time independent variable with the middle variable of the phase angle is shown as the integral for the reciprocal of the response frequency. The numerical values, including the phase portraits, the time-distance curve, the phase-distance curve, and the time-range curve, and the phase-range curve, and the range- frequency curve, and the phase- frequency curve and the response period, are computed. The results are in good agreement with the numerical integral method.

nonlinear RLC circuits；state equation；new solution；numerical emulation

10.13471/j.cnki.acta.snus.2016.03.014

2015-12-26

国家自然科学基金资助项目(11172334)

黄偲(1983年生)，男;研究方向：电子通信;E-mail:lendies@163.con

TN

A

0529-6579(2016)03-0083-06