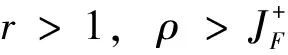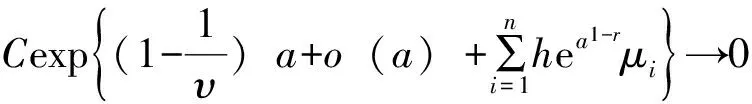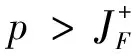非负相依随机变量和的尾部概率一致渐近估计*

唐风琴

(1. 兰州大学数学与统计学院，甘肃 兰州 730000;2. 淮北师范大学数学科学学院，安徽 淮北 235000)

非负相依随机变量和的尾部概率一致渐近估计*

唐风琴1,2

(1. 兰州大学数学与统计学院，甘肃 兰州 730000;2. 淮北师范大学数学科学学院，安徽 淮北 235000)

假设{Xi}i≥1为一列非负不同分布的随机变量，其分布函数属于重尾子族-C族且联合分布满足多元FGMcopula函数。探讨了序列{Xi}i≥1的部分和及随机和的一致渐近估计，推广了相依结构随机变量尾部渐近概率的相应结果.。

精细大偏差；FGM；C族

1 预备知识及主要结果

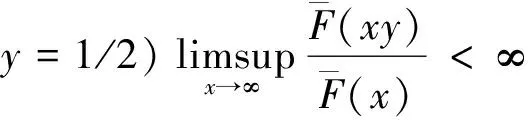
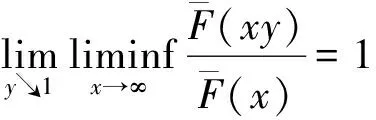
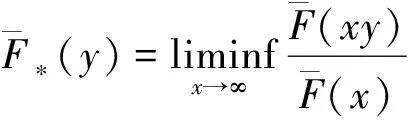
(1)

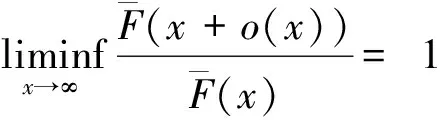
下面介绍著名的Farlie-Gumbel-Morgenstern(FGM)copula函数。n维FGM分布具有如下形式：对所有实数x1,x2,…,xn有

(2)

其中Fi(x)是Xi的分布函数，ajk为实数。若对任意的j,k,ajk=0，则序列x1,x2,…,xn是独立的，本文假设至少存在一个ajk≠0。由Tang等[14]知若Fi(x)是连续的，则有

(3)

进一步地，定义序列x1,x2,…,xn的生存函数为

(4)

β∈[-1,1]。注意到β=0时，Xi和Xj是独立的。同时可得

(5)

满足这种关系的序列又称为尾上渐近独立的(uppertailasymptoticindependent)。 因此，FGM包含了很多的相依结构，如正(负)相依等。现在给出本文的主要结果。

定理2 设随机变量序列{Xi}i≥1满足定理1中条件且对于任意的i,j,存在0

(6)

假设随机过程{N(t),t≥0}与{Xi}i≥1独立，且对任意小的δ>0，{N(t),t≥0}满足

(7)

则对任意的γ>0，当x≥γλ(t),t→∞时一致成立

2 主要结果的证明

首先给出在证明部分和大偏差的下界时一个非常重要的结论。

(8)

令

引理3得证。

其中第二个不等式由(4)式得到。

上界估计。对任意的0<υ<1，沿用引理3中的记号，有

(9)

同引理3的证明类似，令

(10)

其中C为常数，倒数第三步用到引理2的结论。联立(9)和(10)式，由υ的任意性及引理1可得当x≥γn,n→∞时，上界估计得证。

I1+I2+I3

(11)

由δ的任意性，(6)式及定理1可得，当x≥γλ(t)，t→∞时有

(12)

其中C1=C1(c)为正常数。

与I1处理类似，当x≥γλ(t),t→∞时，

(13)

同理可得

(14)

将(12)-(14)式代入(11)式，定理2得证。

[1] 陈传勇. 关于任意同分布随机变量序列最大值不等式及其应用[J]. 中山大学学报(自然科学版)，2015, 52(2): 59-61.

[2]MIKOSCHT,NAGAEVAV.Largedeviationsofheavy-tailedsumswithapplicationsininsurance[J].Extremes, 1998, 1(1): 81-110.

[3]TANGQ,SUQ,JIANGT,etal.Largedeviationsforheavy-tailedrandomsumsincompoundrenewalmodel[J].StatisticsandProbabilityLetters, 2001, 52(1): 91-100.

[4]LIUY,HUYJ.Largedeviationsforheavy-tailedrandomsumsofindependentrandomvariableswithdominatedlyvaryingtails[J].ScienceinChinaSeriesA, 2003, 46(3): 383-395.

[5]NGKW,TANGQ,YANJA,etal.Preciselargedeviationsforsumsofrandomvariableswithconsistentlyvaryingtails[J].JournalofAppliedProbability, 2004(41): 93-107.

[6]TANGQ.Insensitivitytonegativedependenceoftheasymptoticbehaviorofpreciselargedeviations[J].ElectronicJournalofProbability, 2006, 11: 107-120.

[7]LIUL.Preciselargedeviationsfordependentrandomvariableswithheavytails[J].StatisticsandProbabilityLetters, 2009, 79(9): 1290-1298.

[8]CHENY,YUENKC,NGKW.Preciselargedeviationsofrandomsumsinpresenceofnegativedependenceandconsistentvariation[J].MethodologyandComputinginAppliedProbability, 2011, 13(4):821-833.

[9]WANGYB,WANGKY,CHENGDY.Preciselargedeviationsforsumsofnegativelyassociatedrandomvariableswithcommondominatedlyvaryingtails[J].ActaMathematicaSinica-EnglishSeries, 2006, 22(6): 725-1734.

[10]WANGKY,YANGY,LINJG.Preciselargedeviationsforwidelyorthantdependentrandomvariableswithdominatedlyvaryingtails[J].FrontiersofMathematicsinChina, 2012, 7(5): 919-932.

[11]TANGQ,TSITSIASHVILIG.Preciseestimatesfortheruinprobabilityinfinitehorizoninadiscretetimemodelwithheavy-tailedinsuranceandfinancialrisks[J].StochasticProcessesandTheirApplications, 2003, 108(2): 299-325.

[12]TANGFQ,BAIJM.Preciselargedeviationsforaggregatelossprocessinamulti-riskmodel[J].JournaloftheKoreanMathematicalSociety, 2015, 52(3): 447-467.

[13]HEW,CHENGD,WANGY.Asymptoticlowerboundsofpreciselargedeviationswithnonnegativeanddependentrandomvariables[J].StatisticsandProbabilityLetters, 2013, 83(1): 331-338.

[14]TANGQ,VERNICR.Theimpactonruinprobabilitiesoftheassociationstructureamongfinancialrisks[J].StatisticsandProbabilityLetters, 2007, 77(14): 1522-1525.

The uniformly asymptotic estimate for the tail probability of the sums of nonnegative and dependent random variables

TANGFengqin1,2

(1. School of Mathematics and Statistics, Lanzhou University, Lanzhou 730000, China;2. School of Mathematics Sciences, Huaibei Normal University, Huaibei 235000, China)

Suppose that {Xi}i≥1isasequenceofnonnegativeandnon-identicallydistributedrandomvariableswhichbelongtothesubclassofheavy-taileddistributions-classC.ThemultivariatedistributionfunctionoftherandomvariablesisgovernedbytheFGMcopulafunction.Theuniformlyasymptoticestimateforthepartialsumsandrandomsumsofthesequence{Xi}i≥1arestudied,respectively.Theobtainedresultsextendthecorrespondingasymptoticestimateofthetailprobabilityofthedependentrandomvariables.

precise large deviations; FGM; consistently varying

10.13471/j.cnki.acta.snus.2016.03.009

2015-11-30

安徽省高校自然科学研究一般资助项目(KJ2014B15)

唐风琴(1983年生)，女；研究方向：概率论极限理论;E-mail:tfq05@163.com

O211.65;O

A

0529-6579(2016)03-0055-04