一种HSV空间上分层压缩感知的图像检索算法*

周 燕，曾凡智,赵慧民

(1.佛山科学技术学院计算机系，广东 佛山 528000;2.广东技术师范学院电子与信息学院, 广东 广州 510665)

一种HSV空间上分层压缩感知的图像检索算法*

周 燕1，曾凡智1,赵慧民2

(1.佛山科学技术学院计算机系，广东 佛山 528000;2.广东技术师范学院电子与信息学院, 广东 广州 510665)

通过构建二维压缩感知测量模型，提出一种分层HSV特征和分层纹理特征提取与图像检索新算法。在图像HSV空间上引入网格离散划分和分层映射算子，定义一种基于HSV网格空间上的分层映射矩阵和拟灰度共生矩阵；设计归一化Gauss随机矩阵作为测量矩阵，使用二维压缩感知测量模型对上述两种矩阵进行压缩采样；采用PCA(PrincipalComponentAnalysis)方法获取上述两种分层采样矩阵的特征值序列，作为图像的分层HSV特征与分层纹理特征。最后融合上述两类特征综合计算图像间的整体相似度并实现图像检索。仿真实验表明，上述两类特征具有很好的可区分性，有效提高了图像检索效率，特别对复杂背景的图像检索性能更优

二维压缩感知；分层纹理特征；分层HSV特征；拟灰度共生矩阵

为了充分利用互联网环境下产生的海量数字图片资源，需要对其进行有效的存储、管理、重用及高效检索。基于内容的图像检索(Content-Based Image Retrieval, CBIR)正是解决此类问题的有效方法，也是当前图像分析、计算视觉中最为活跃的领域之一。CBIR主要以颜色、纹理、形状等底层物理特征作为图像内容特征，研究重点包括图像内容特征的高效提取及相似度计算两个方面。由于单一的图像底层特征不能全面概括图像内容，融合多类特征实现图像检索成为主要研究方向。文献[1]提出了一种综合颜色、形状和纹理特征的图像检索方法，但权值系数的选择对检索精度影响较大。文献[2]提出了一种融合语义特征和视觉特征的纹理图像检索方法，但需要进行语义转换及反馈处理。结合人眼视觉特性，文献[3]提出了一种基于HSV空间的彩色边缘图像检索方法，但提取边缘特征丰富程度稍欠缺。文献[4]提出了在HSV空间上提取均值、标准误差等颜色特征，并采用灰度共生矩阵提取纹理特征的图像检索方法，但相似度计算过程较为复杂。文献[5]基于多尺度几何分析的Contourlet变换提取分层图的颜色、纹理特征，结合相关反馈机制提出了一种较有效的图像检索方法，但需要人机交互式参与。文献[6]提出了一种融合颜色、纹理、边界及形状特征的逐步逼近的图像检索方法，减少了初始候选集的大小，但未能考虑各类特征融合的相似度计算。文献[7]通过量化HSV颜色空间及结合颜色和纹理特征的特征向量构建权重系数，提出了一种融合颜色特征和纹理特征的图像检索方法。文献[8]通过提取轮廓段序列及计算基于动态规划的近似串匹配链的相似性，提出了一种基于用户绘制草图的图像检索方法。在文献[9]中，作者对压缩感知理论应用于图像快速检索中做了有益的探索。在文献[10]中，作者提出了一种行列二维压缩测量模型，提取图像特征并应用于图像检索，取得较好的效果，但计算量高度依赖于图像的分块数。综上所述，目前相关算法在高效特征提取及相似度计算等方面仍有待进一步提升。

本文基于压缩感知理论[11-13]，采用二维压缩测量模型，设计满足RIP条件的行列测量矩阵[13]，通过分层方式对图像HSV进行分层映射，获取图像分层HSV特征及分层纹理特征，设计一种融合分层HSV特征和纹理特征的图像检索算法。研究图像HSV空间上的离散划分与分层映射算子，定义一种基于网络空间的拟灰度共生矩阵，采用二维压缩测量过程生成图像压缩测量值并构成矩阵，采用PCA方法获取协方差矩阵特征值序列，作为图像的两类内容特征向量，并提出多特征融合相似度度量指标。

1 相关工作

1.1 二维压缩感知测量模型

对二维可稀疏信号直接采用二维压缩感知测量过程能避免设计测量矩阵的维数灾难，同时也能保持图像像素点之间的相对位置。自然图像在离散余弦变换DCT、离散傅里叶变换DFT、离散小波变换DWT等变换下是二维可稀疏信号[14]。文献[10]、[14]中提出了一种2D的压缩感知模型如下：

(1)

其中X∈RN×N代表二维图像信号，Φ1,Φ2∈RM×N分别是行、列压缩测量矩阵，Y∈RM×M代表二维压缩测量值。若Φ1、Φ2选取合适归一化Gauss随机矩阵，则通过等价l1范数优化问题求解能够高概率地由测量值Y重构二维信号量X[14]。因此采用公式(1)获取少量二维测量值Y可以作为原始图像X的一类内容特征。

1.2 压缩测量矩阵

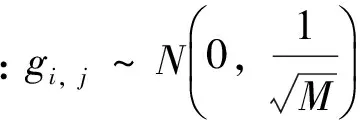
通过对Gauss随机矩阵进行列归一化处理，选定测量矩阵Φ1=Φ2=Φ，其构造如公式(2)所示：

(2)

2 图像特征提取

特征提取算法是CBIR的最重要研究内容，检索的准确率主要取决于图像特征的提取。在本文算法中，主要提取分层HSV特征和分层纹理特征。

2.1 分层HSV特征的提取

对于大小为N×N的二维RGB图像X，首先通过颜色变换把图像从RGB空间变为HSV空间[3]。然后通过二维压缩感知模型获取图像分层HSV特征，其算法过程如下。

1)二维图像的HSV空间网格离散化：选取H、S、V轴的离散点对HSV空间进行离散网格划分，每个立方体网格单元记为Vl，对网格单元按照行优先次序排序，得到网格单元序列：Vl(l=1,2,…,L)，其中L代表网格单元总数。在网格单元Vl上，定义原始图像的稀疏分层映射算子

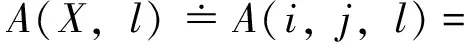
(3)

其中l=1,2,…,L；i,j=1,2,…,N。H(i,j),S(i,j),V(i,j)分别代表像素点(i,j)处HSV值。

2)分层HSV特征：对每个选定网格单元Vl，矩阵(A(i,j,l))N×N反映了图像HSV空间上Vl邻域内的像素点在平面坐标上相对位置的分布状况。若H、S、V各分量的分层数选取合适，则第l层上矩阵(A(i,j,l))N×N是一个稀疏二维信号，采用二维压缩感知模型公式(1)，对其进行二维压缩感知测量：

Yl=TDCS∘A=

(4)

其中l=1,2,…,L。

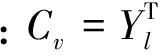
第l层的分层HSV特征向量定义为λl：

(5)

其中l=1,2,…,L代表分层的层数。

3)分层HSV特征的可区分性：分层二维压缩感知测量值Yl∈RM×M及特征向量λl，比传统颜色直方图具有更好可区分性。

设有如图1所示的两个子图T，T′，其形态如下。

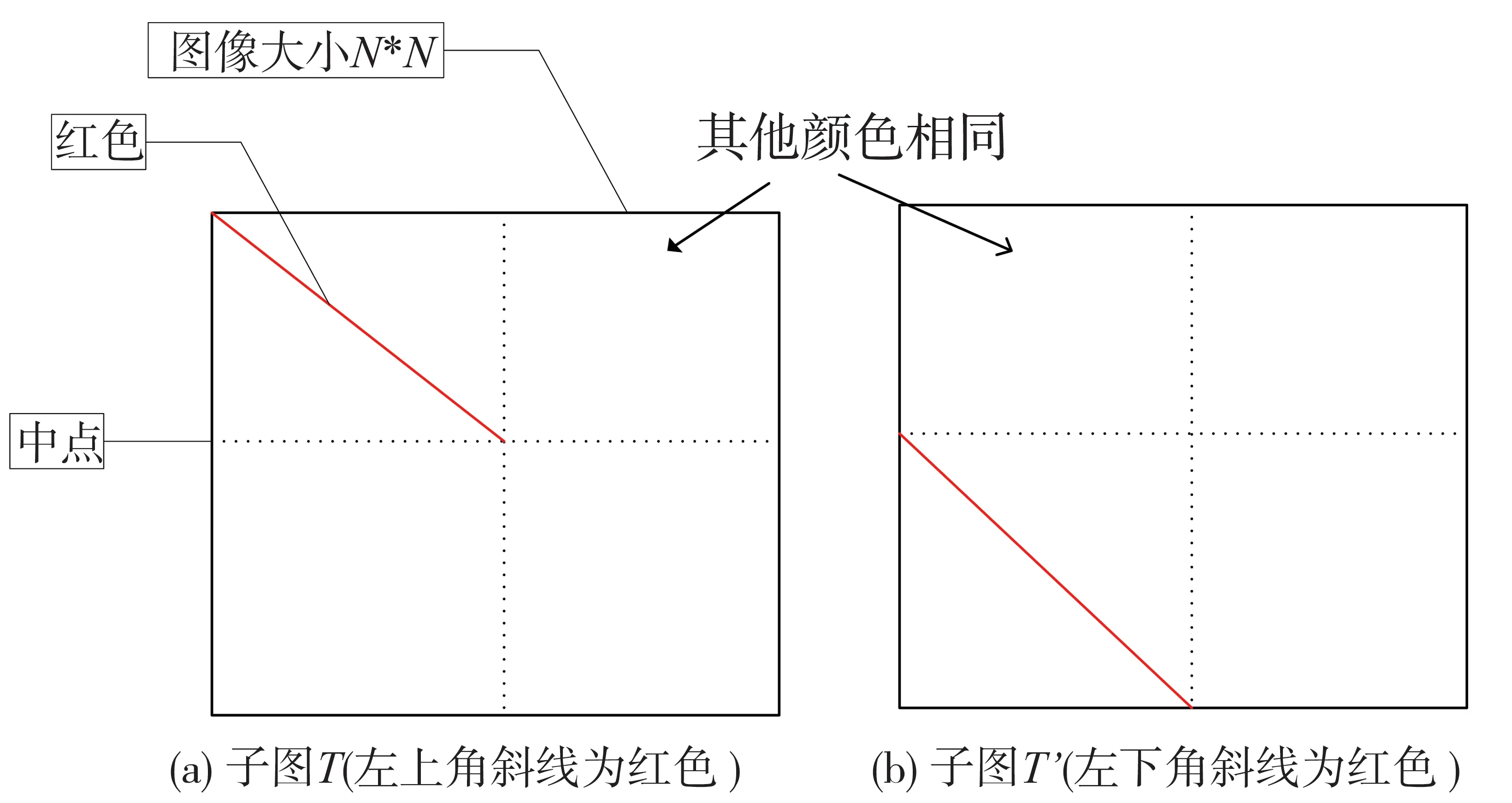
图1 分层测量特征差异分析图Fig.1 Difference analysis for Hierarchical measurement feature

如图1所示，把子图T，T′划分为大小N/2×N/2的4个子块，子图T的左上角子块与子图T′的左下角子块有红色对角线，其它子块的颜色都相同。按照颜色直方图进行计算，这两个子图对应的传统颜色直方图完全一样。

针对子图T，T′，下面分析本文提出的分层压缩测量特征的差异。

假设红色分层在第l层上，经过分层映射后，得到如下的分块矩阵：

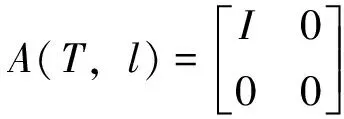
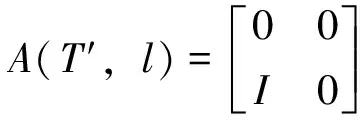
其中I，0分别代表N/2×N/2的单位矩阵和零矩阵。

对测量矩阵Φ1，Φ2∈RM×N也做如下分块：

其中Φ11，Φ12，Φ21，Φ22∈RM×(N/2)。

针对子图T，T′，采用公式(4)得到如下的分层二维压缩感知测量值：

在第l层上，它们的差异如下：

(6)

(7)

其中c0，c0′是只与测量矩阵Φ1，Φ2相关的常数。

公式(6)、(7)表明，针对子图T，T′的分层压缩测量值Yl以及特征向量λl，由于它们保留了颜色空间分层邻域与像素点的位置关系，因此能够体现更精细化的差异，比传统的颜色直方图具有更好的可区分性。

2.2 分层纹理特征的提取

拟灰度共生矩阵与分层纹理特征：传统灰度共生矩阵是用来描述纹理特征的经典数据结构，是关于图像灰度级在空间分布上的综合描述，通过提取有意义的统计特性来表达图像的纹理特征。灰度共生矩阵的构造依赖于像素点之间的方向和距离。在HSV空间网格划分基础上，本文提出一种基于网格划分的拟灰度共生矩阵，是关于图像网格邻域在空间分布上的综合描述。拟灰度共生矩阵与方向θ和距离d这两个参数有关，其定义如下：

M(θ,d)=(Ml1l2(θ,d))L×L

Ml1l2(θ,d)=

其中l1,l2=1,2,…,L代表分层的层数，#(·)表示集合基数。方向θ和距离d参数可选取如下序列：

当参数θ,d选取不同角度、不同距离的参数时，矩阵M(θ,d)可以看作是传统灰度共生矩阵的推广，它集中反映了HSV颜色空间分层邻域间的纹理特征。

矩阵M(θ,d)是二维可稀疏信号，采用公式(1)的二维压缩感知模型进行测量，得到与纹理相关的分层测量值：

(8)

其中l=(i-1)×L1+j;i=1,2,…,L1;j=1,2,…,L2;l=1,2,…,L3；L3=L1×L2。

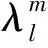
(9)

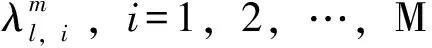
3 相似度计算

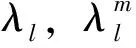
经过归一化处理后得到图像间的整体相似度：

(10)

4 实验结果与分析

本文采用的开发平台为Matlab2012和VisualStudio2008，测试平台为联想M440S个人电脑，硬件配置：CPU：Intel(R)I5-4200U4×2.4GHz，内存：4GBDDR3L，操作系统为32位的Windows7SP1。采用标准Corel图像集，从中选取1 000幅图像进行仿真实验，共10类，每类100幅图像，包括非洲、海滩、建筑、公交车、恐龙、大象、花、马、雪山和食物。图像大小为256×384和384×256。

4.1 分层HSV特征与分层纹理特征的仿真实验

为了进一步分析分层HSV特征和分层纹理特征，选取Corel 1 000图像集中的五类图像，分别是马、花、非洲、恐龙、食物，对这五类图像分层纹理特征值和分层HSV特征值进行对比分析。分层纹理特征值对比如图2所示，同类图像的分层特征有较高的相似度，而不同类别图像的差别是非常明显的。对分层HSV特征作同样分析，图3是五种不同类别图像的HSV分层特征对比图，图中所示是对应的分层HSV特征向量λl的2-范数值，不同类别图像的差别是非常明显的。

以上仿真实验表明，本文提取的分层HSV特征与分层纹理特征对不同类别的图像具有较高的可区分性,为提高图像的检索准确率奠定了基础。

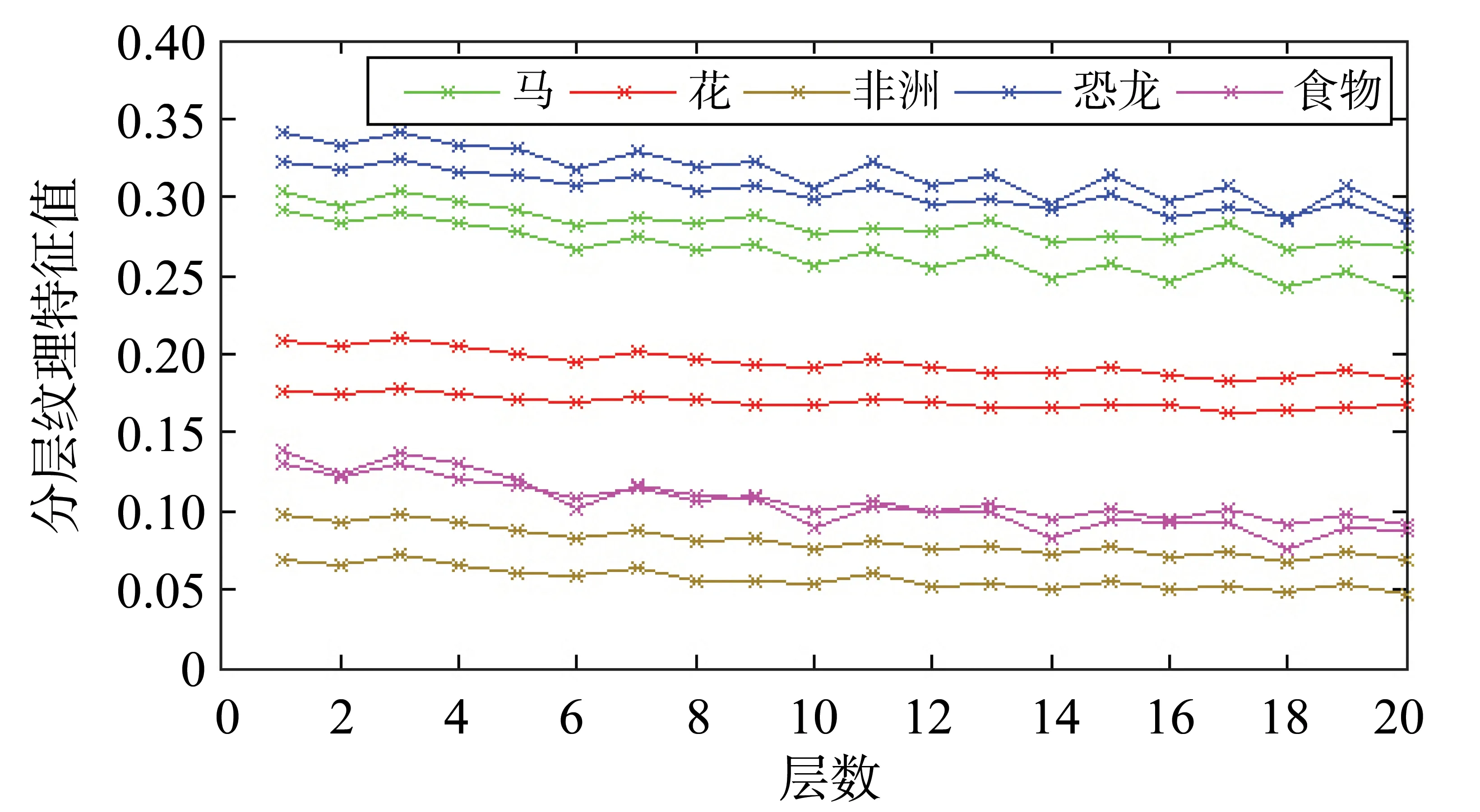
图2 五类图像的分层纹理特征值对比图Fig.2 Comparison of hierarchical texture features for five kinds of images

图3 五类图像的分层HSV特征值对比图Fig.3 Comparison of hierarchical HSV features for five kinds of images

4.2 本文算法检索结果

本文采用256维的分层HSV测量特征向量和基于拟灰度共生矩阵的分层纹理测量特征向量进行组合检索。由于非洲和食物这两类图像的背景较复杂，在已有的检索算法中其检索准确率不高。利用本文算法得到的检索结果如图4-5所示，每页包含25幅图像，其中第一页的检索结果全部相关，表明本文算法的检索准确率较高。

图4 “非洲”图像的检索结果Fig.4 Retrieval result for African image

图5 “食物”图像的检索结果Fig.5 Retrieval result for Food image

4.3 不同算法的检索性能比对分析

为了客观地评价各种算法的图像检索性能，本文以查准率和查全率作为评价指标，采用Corel1 000作为测试图像集，从每类图像中任意选取20幅图像作为检索样本，对各类图像设置相应的权值。本文算法与文献[1]、文献[4]的图像查准率和查全率的对比结果如图6-7所示。从图中可以看出，本文算法具有较好的性能，多种类别图像的查准率超过80%，总的平均查准率达到82.2%，其中有6类图像的平均查准率优于文献中得到的平均查准率。本文算法的平均查准率比文献[1]高出2.45%，比文献[4]高出5.75%。

多种类别图像的查全率超过50%，平均查全率达到47.6%，其中有9类图像的平均查全率优于文献中得到的平均查全率。本文算法的平均查全率比文献[1]高出7.9%，比文献[4]高出10.5%。

图6 平均查准率对比结果Fig.6 The comparative analysis for average precision

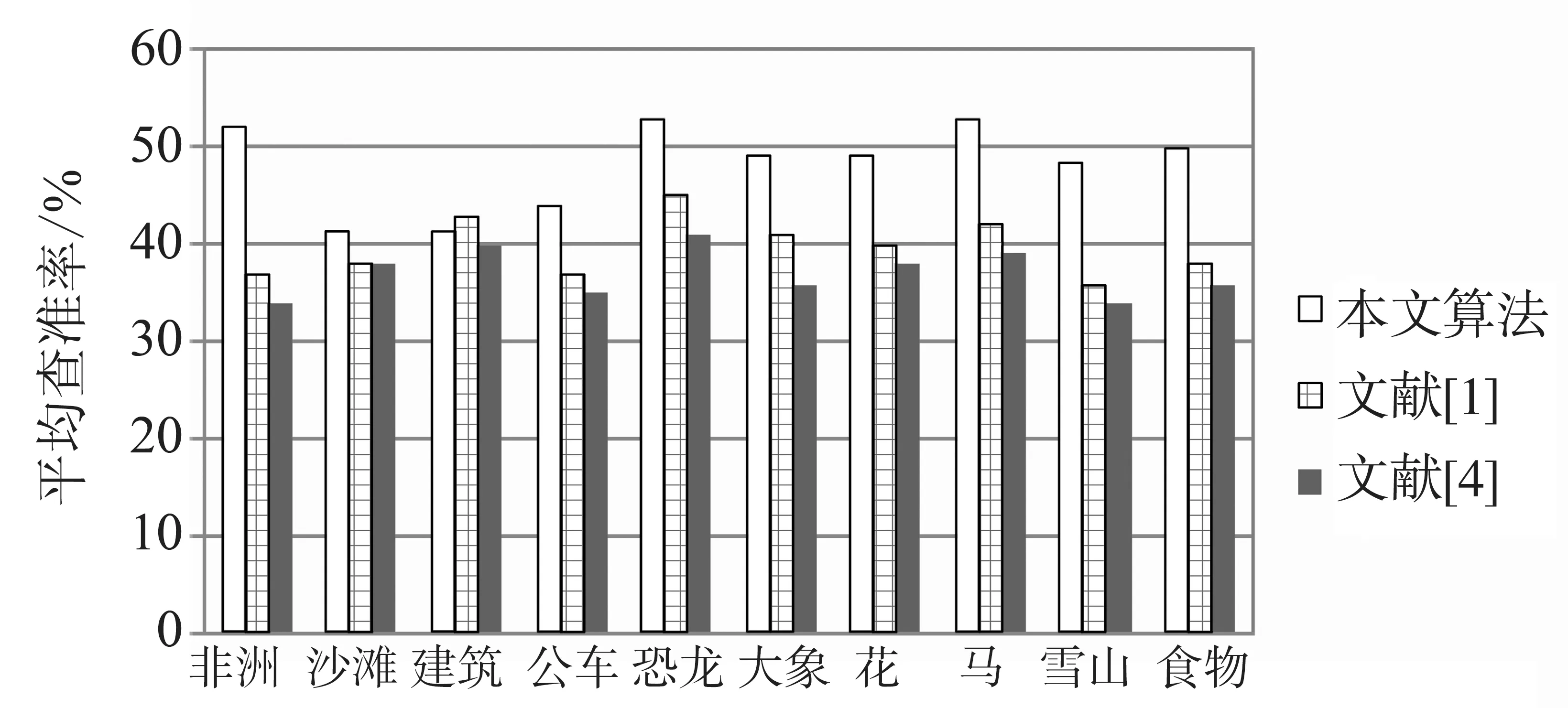
图7 平均查全率对比结果Fig.7 The comparative analysis for average recall

5 结 论

由于用HSV表达图像更接近人类对颜色概念的理解，因此在计算机视觉领域获得广泛应用。首先在图像HSV空间上引入网格离散和分层映射思想，定义一种基于HSV网格空间的拟灰度共生矩阵。然后构建归一化Gauss随机矩阵作为测量矩阵，采用二维压缩感知测量模型对HSV分层映射矩阵、拟灰度共生矩阵进行压缩采样。最后采用PCA方法提取图像的分层HSV特征与分层纹理特征，并融合这两类特征综合计算图像的相似度。仿真实验结果表明这两类特征具有很好的可区分性，对复杂背景的图像检索具有较好的效果。本文对二维压缩感知理论与图像分析的结合做了有益探索，今后将在形状、边界等内容特征的压缩感知采样方面作进一步研究，融入更多内容特征以提高图像检索效率。

[1] 张永库,李云峰,孙劲光. 基于多特征融合的图像检索[J].计算机应用,2015, 35(2):495-498.

[2] 李清勇,施智平,史忠植. 综合语义特征和视觉特征的二阶段纹理图像检索[J].计算机辅助设计与图形学学报,2008,20(4):499-505.

[3] 杨红颖,吴俊峰,于永健,等.一种基于HSV空间的彩色边缘图像检索方法[J].中国图象图形学报,2008,13(10): 2035-2038.

[4]LAICC,CHENYC.Auser-orientedimageretrievalsystembasedoninteractivegeneticalgorithm[J].IEEETransactionsonInstrumentationandMeasurement, 2011, 60(10): 3318-3325.

[5]KUNDUMK,CHOWDHURYM,BULOSR.Agraph-basedrelevancefeedbackmechanismincontent-basedimageretrieval[J].Knowledge-BasedSystems, 2015,73:254-264.

[6]SHRIVASTAVAN,TYAGIV.Anefficienttechniqueforretrievalofcolorimagesinlargedatabases[J].ComputersandElectricalEngineering, 2014,11(9) :1-14.

[7]YUEJ,LIZB,LIUL,FUZT.Content-basedimageretrievalusingcolorandtexturefusedfeatures[J].MathematicalandComputerModelling, 2011, 54(3/4): 1121-1127.

[8]PARISS,MITTALA.Similarity-invariantsketch-basedimageretrievalinlargedatabases[J].EuropeanConferenceonComputerVision, 2014, 8694: 398-414.

[9] 周燕,曾凡智,卢炎生,等.基于压缩感知的图像检索方法研究[J]. 中山大学学报(自然科学版),2014,53(1):57-62.

[10] 周燕,曾凡智,卢炎生,等.面向制造领域的三视图模型组件快速检索方法研究[J],中山大学学报(自然科学版),2014,53(4):62-68.

[11]CANDESE,WAKINM.Anintroductiontocompressivesampling[J].IEEESignalProcessingMagazine, 2008, 25(2): 21-30.

[12] 焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1651-1662.

[13] 许志强. 压缩感知[J]. 中国科学(数学),2012,42(9): 865-877.

[14]CHENG,LIDF,ZHANGJS.Iterativegradientprojectionalgorithmfortwo-dimensionalcompressedsensingsparseimagereconstruction[J].SignalProcessing, 2014, 104:15-26.

An image retrieval algorithm based on hierarchical compressive sensing in HSV space

ZHOUYan1,ZENGFanzhi1,ZHAOHuimin2

( 1.Department of Computer Science, Foshan University, Foshan 528000, China;2.School of Electronic and Information Engineering, Guangdong Polytechnic Normal University,Guangzhou 510665, China)

By constructing a two-dimensional (2D) compressive sensing (CS) measurement model, a new image retrieval algorithm is proposed by extracting hierarchical HSV features and texture features. Firstly, the ideas of grid discrete partition and hierarchical mapping in HSV space are introduced, and hierarchical mapping matrix and similar GLCM in HSV grid space are defined. Secondly, the normalized Gauss random matrix is designed as measurement matrix, and compressive sampling on the above two matrixes is performed by 2D CS measurement model. With using PCA(Principal Component Analysis), the feature sequences as hierarchical HSV features and texture features are obtained from the above two hierarchical sampling matrixes. Finally, the above two features are infused to compute the overall similarity among images. Experimental results show that the above two features have good discrimination. It can improve the efficiency for image retrieval, and has good performance especially for images with complex backgrounds.

two-dimensional compressive sensing; hierarchical texture feature; hierarchical HSV feature; similar GLCM

10.13471/j.cnki.acta.snus.2016.03.013

2015-12-26

广东省自然科学基金资助项目(2015A030313635，2015A030313672,2016A030311013)；广东省科技计划资助项目(2014A010103037)；广东省教育厅省级重大资助项目(2014KZDXM060,2015KGJHZ021)；广东省教育厅特色创新类资助项目(2015KTSCX153)；佛山市科技创新专项资金资助项目(2015AG10008，2014AG10001)；佛山科学技术学院优秀青年教师培养计划资助项目(fsyq201411)

周燕(1979年生)，女；研究方向：图像处理，数字水印;E-mail:zhouyan791266@163.com

TP

A

0529-6579(2016)03-0077-06